基于流固耦合的客车风窗玻璃风致振动特性

陶莉莉，杜广生，刘丽萍，雷 丽

（1.山东交通学院 运输车辆检测、诊断与维修技术交通行业重点实验室，山东 济南250023；2.山东大学 能源与动力工程学院，山东 济南250061）

在客车高速行驶过程中，前方大面积的风窗玻璃由于承受很大的风压和脉动气流压力，变形增大，易产生应力集中；而脆性玻璃材料内部存在的微裂纹以及材料的不均匀性使其在集中应力作用下易产生破碎现象，严重影响行车安全.尤其在目前客车风窗玻璃趋于轻量化的情况下，开展风窗玻璃风致振动研究有着重要意义.

目前汽车风窗玻璃特性的研究主要集中在力学特性及碰撞特性等方面，关于抗风压特性的研究较少.Scigliano等［1］采用有限元方法对自由状态和实际边界条件下某轿车前风窗玻璃动力学特性进行了研究.沈浩等［2］分别从空气动力学和车身动态特性两个角度分析了客车风窗玻璃破裂的机理，指出稳态情况下空气压力对风窗玻璃的强度影响很小，但该研究未考虑风致振动和玻璃变形双向耦合的影响因素.陈黎［3］和封进［4］采用施加静压力的实验方法，得到客车前风窗玻璃变形量与所受压力的关系，模拟了风窗玻璃受风压时的受力情况，但该实验方法与实际的汽车动态风压受力存在较大差别.此外，石得春［5］、王立闯等［6］对高速列车侧窗的风压瞬态响应及疲劳性能等进行了相关研究.

上述针对风窗玻璃的研究在分析时均未考虑流固耦合的影响.实际上客车在高速行驶情况下受到流场的作用，一方面车身表面产生风压变形，材料内部会产生应力重分布；另一方面车身变形在一定程度上会影响流场的压力分布和流速变化.本文采用流固耦合的方法研究了某国产高速客车夹层式风窗玻璃的风压变形和受力特性，分析了厚度变化对风窗玻璃变形及应力的影响规律.

1 高速客车流固耦合计算模型

计算采用ADINA软件，分别建立固体模型和流体模型进行流固耦合计算，得到高速客车瞬态气动特性及风窗玻璃风致振动特性.

1.1 流固耦合的数学模型

1.1.1 流体计算模型

客车采用分离涡模拟模型（deta ched eddy simulation，DES）对流场进行数值模拟计算.把流场划分为两部分，在网格足够密的近壁面区域采用大涡模拟的Smagorinsky Lilly亚格子模型；其他区域采用雷诺应力模型中的Spalart-Allmaras模型［7］.

1.1.2 固体有限元数学模型

固体结构采用有限元分析方法，将玻璃和钢材均视为弹性体，根据弹性结构动力学有限元方程：

1.1.3 流固耦合模型［8］

式中，Ff和Fs分别为流体方程和结构方程.

1.2 客车的物理模型

1.2.1 固体模型建立与网格划分

为节省计算时间，考虑到客车车身结构的对称性，采用半车模型；风致振动特性研究主要考虑风窗玻璃，忽略车轮的耦合作用.由于车身厚度方向尺寸远小于长、宽方向尺寸，单元类型采用壳单元进行离散化，网格总数为7 795.车身网格如图1所示.

图1 客车车身的有限元模型Fig.1 Finite element model of the bus body

1.2.2 风窗玻璃的力学特性及计算方法

目前客车风窗玻璃普遍采用聚乙烯醇缩丁醛（polyvinyl butyral，PVB）夹层玻璃，如图2所示.图中，t1、t2、h分别为单片玻璃厚度和PVB胶片厚度.外层玻璃为脆性非线性材料，中间层的PVB胶片是粘弹性材料.Timmen等［9］的研究表明在准静态加载条件下PVB夹层玻璃荷载与位移基本呈线性关系.基于此特性，可以采用等效厚度法计算夹层玻璃的变形及应力.

图2 PVB夹层玻璃结构示意图Fig.2 The structural schematic diagram of PVB laminated glass

欧洲标准草案prEN13474-1：1999［10］和prEN13474-2：2000［11］给出夹层玻璃等效厚度teq计算公式为

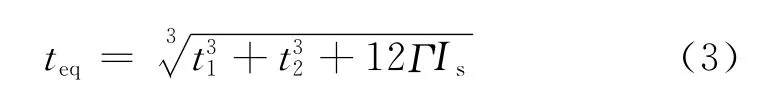
式中：Γ为剪力传递系数，普通夹层玻璃Γ=0，钢化夹层玻璃短期载荷时Γ=1，长期载荷时Γ=0；Is为与夹层玻璃各层厚度有关的结构系数.

由于高速客车的风窗玻璃为普通夹层玻璃，Γ=0，则式（3）变为

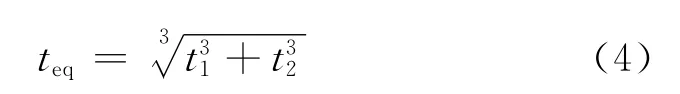
本研究采用式（4）计算PVB夹层玻璃的等效厚度.对高速客车普遍采用的4mm+0.76mm（PVB）+4mm夹层玻璃，其等效厚度为5.04mm.

1.2.3 材料、边界条件及控制参数

风窗玻璃材料参数如下：弹性模量E为70 000 MPa，泊松比μ为0.24，密度为2 500kg·m3.

风窗玻璃和车身部分设置为流固耦合界面，车底板设置为固定约束，车身纵向中面设为对称边界条件.由于风压引起的变形量远小于等效厚度，因此采用弹性小挠度变形理论［12］，运用瞬态隐式求解方法进行模拟计算.

1.3 流体物理模型

在流体模型计算域设置时，客车模型上部取3B（B为客车模型的宽度），左右两侧各取3B，长度方向车前取8B，车后取20B.计算域尺寸为80m×15 m×10m.网格数目约为110万.

入口边界条件采用速度入口.0～1s时间内进行静力计算，得到重力作用下的平衡状态.在1～2s时入口速度从0逐渐加速到35m·s-1.这种逐渐加载的方式有利于计算的收敛.出口边界条件采用压力出口.时间步长设置为0.001s，共计算了2 000时间步［7］.

1.4 计算方法验证

流固耦合计算方法的实验验证在山东大学低速风洞中进行，利用一个迎风面安装玻璃的类客车体进行了风致振动的实验研究，实验结果与模拟计算结果一致，表明计算方法的正确性.具体内容见文献［7］.本文采用的流固耦合计算方法与文献［7］采用的方法一致.

2 风窗玻璃风致振动分析

2.1 风压变形时程分析

本文主要分析进入匀速阶段的风压变形情况.以风窗玻璃的近似中心点170节点作为研究对象，分析该节点的变形时程曲线.图3和图4分别给出170节点的位移和加速度在x、y两个方向随时间变化情况.因170节点位于风窗玻璃的中心对称面上，z向速度和加速度均为0.

图3 170节点变形时程曲线Fig.3 Time-deformation curves of 170nodes

由图3和图4知，在与来流方向相反的y方向，t=2.0s之后的匀速过程初期，由于y向加速度迅速增大，y向变形量对应瞬间增大并剧烈波动变化，最大变形量达到0.22mm；匀速过程后期加速度波动平缓，y向变形量波动也相应平缓，并趋于一个稳定值.在垂直于地面的x方向，加速度变化趋势和变形趋势与y向基本一致，但加速度和变形量明显减小，说明来流方向产生的变形量是风窗玻璃风压变形的主要构成.

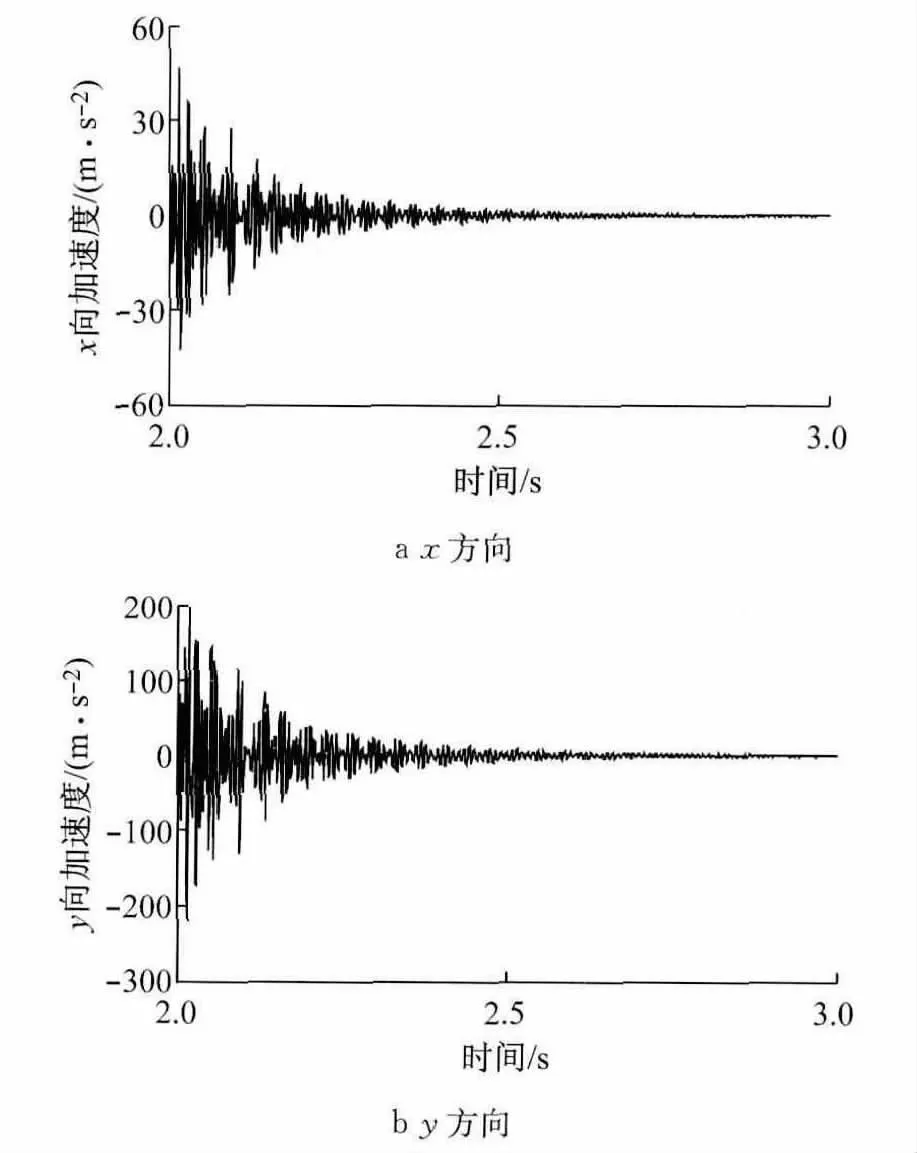
图4 170节点加速度时程曲线Fig.4 Time-acceleration curves of 170nodes

第2.1节分析表明，在客车与前方来流相对速度变化的过程中，重力、来流速度变化及引起的惯性力共同叠加，会加剧来流与玻璃之间的相互耦合作用，导致风窗玻璃产生剧烈的振动和变形波动.

2.2 应力时程分析

在流场中，风窗玻璃由于风压作用产生弹性变形而引起应力效应.

170节点的应力值随时间变化情况如图5所示.在t=2.0s之后的匀速过程初期，虽然来流速度保持不变，但由于流固耦合作用，170节点的应力剧烈波动变化，之后迅速衰减并趋于平缓，t=2.6s后应力变化趋于平稳，在某时均值附近小幅波动变化.

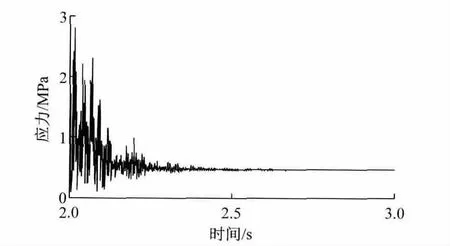
图5 170节点的应力时程曲线Fig.5 Time-stress curves of 170nodes

第2.2节分析表明，采用流固耦合计算方法可以获得风窗玻璃瞬态应力变化情况，尤其来流速度变化及客车行驶工况变化等因素会直接影响瞬态应力值，且最大应力值远远大于时均值，会明显增大玻璃破坏的概率，影响客车行驶安全.而以往采用施加静荷载方法得到的风窗玻璃应力为静态应力值，不能体现出其瞬态的变化情况.

3 玻璃厚度变化对风窗玻璃风压特性影响

高速客车目前采用的夹层玻璃厚度范围多为4 mm+0.76mm（PVB）+4mm 至6mm+0.76mm（PVB）+6mm.由于面积大，因此轻量化问题较为突出.

对4mm+0.76mm（PVB）+4mm结构风窗玻璃的计算表明，该玻璃有足够的薄型化设计空间.采用等效厚度法对组合结构为3.5mm+0.76mm（PVB）+3.5mm（方案2）和3mm+0.76mm（PVB）+3mm（方案3）两种薄型风窗玻璃进行了计算，并与4mm+0.76mmPVB+4mm（方案1）风窗玻璃进行对比，分析厚度变化对风窗玻璃风压特性的影响.方案2和3的风窗玻璃等效厚度分别为4.41mm和3.78mm.

3.1 厚度变化对风窗玻璃变形影响

以风窗玻璃170节点为基准选取9个节点，其位置如图6所示.

图6 9个节点的位置示意图Fig.6 Schematic diagram of nine nodes’location

图7和图8分别给出三种方案对应的风窗玻璃9个节点在匀速阶段的最大变形量与时均变形量的变化情况.由图知，随着厚度减小，各节点最大变形量和时均变形量均有较大增幅，尤其中心节点170节点变化最大，其方案3的最大变形量比方案一的最大变形量增大74.1%，时均变形量增大35.0%.

图7 三种方案9个节点最大变形量对比Fig.7 The contrast of nine nodes’max deformation in three schemes

图8 三种方案9个节点时均变形量对比Fig.8 The contrast of nine nodes’time-average deformation in three schemes

从轻量化角度，方案2的风窗玻璃重量减少10.39kg，下降15.9%；方案3的风窗玻璃重量减少20.778kg，下降24.1%，轻量化效果较显著.

3.2 厚度变化对风窗玻璃应力的影响

图9和图10分别给出三种方案对应的9个节点在匀速阶段的瞬态最大应力值与时均应力值对比结果.

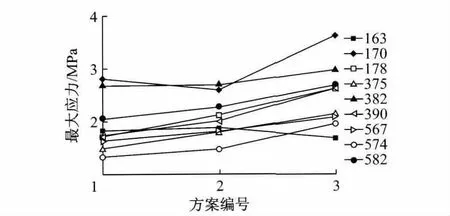
图9 三种方案9个节点最大应力值对比Fig.9 The contrast of nine nodes’max stress in three schemes

由图9和图10知，当厚度变化时，风窗玻璃各节点的应力变化较复杂.9个节点的最大应力值大多随厚度降低而增大.以178节点为例，方案2比方案1最大应力增大22.0%，方案3比方案1最大应力增大52.0%.但163节点和170节点出现不规律变化现象.当风窗玻璃厚度减小时，二者最大应力的变化趋势相反，163节点先增大后减小，170节点则先减小后增大.

图10 三种方案9个节点时均应力值对比Fig.10 The contrast of nine nodes’time-average stress in three schemes

风窗玻璃厚度减小，9个节点的时均应力值基本呈增大趋势.163节点的时均应力值，方案2比方案1增大22.5%，方案3比方案1增大50.0%.582节点则分别增大15.4%和38.4%.178点的时均应力随玻璃厚度减小变化不大.

综上分析，风窗玻璃厚度减小，风压变形明显增大，但对应力的影响较小且变化不规律.从变形及应力的破坏机理出发，通过优化设计，可进一步实现风窗玻璃及客车的轻量化.

4 结论

本文采用流固耦合方法对高速客车风窗玻璃风致振动特性进行了研究，主要结论如下：

（1）在行驶过程中高速客车风窗玻璃受来流影响产生风压变形.由加速过程进入匀速过程的初始时刻，风压变形量相对较大且剧烈波动变化，之后变形量迅速下降，波动趋于平缓，并逐渐接近某时均值.该现象说明在客车与前方来流相对速度变化的过程中，惯性力会加剧来流与玻璃之间的相互耦合作用，导致风窗玻璃变形量剧烈波动变化.

（2）通过流固耦合计算获得了风窗玻璃的瞬态应力变化规律.在客车高速行驶工况下，风荷载引起的瞬时最大应力值远高于时均应力值.因此在风窗玻璃设计时，需充分考虑客车运行工况变化的影响.

（3）对三种不同厚度的风窗玻璃计算结果表明，风窗玻璃厚度减小，风压变形明显增大，但应力影响较小且不规律变化.该分析方法可用于风窗玻璃的轻量化设计.

［1］ Scigliano R，Scionti M，Lardeur P.Verification，validation and variability for the vibration study of a car windscreen modeled by finite elements［J］.Finite Elements in Analysis and Design，2011，47：17.

［2］ 沈浩，谢硕，姚晓冬，等.高速客车风窗玻璃破裂机理分析［J］.客车技术与研究，2002，24（6）：6.SHEN Hao，XIE Shuo，YAO Xiaodong，et al.Crack mechanism analysis of the windshield of high speed bus［J］.Bus Technology and Research，2002，24（6）：6.

［3］ 陈黎.前挡风玻璃爆裂对比实验［J］.客车技术与研究，2008（1）：40.CHEN Li.Contrast test of burst of front windshield［J］.Bus Technology and Research，2008（1）：40.

［4］ 封进.大变形条件下客车前风挡玻璃的强度实验方法［J］.城市车辆，2008（7）：42.FENG Jin.Test method of intensity of bus front windscreen under large deformation［J］.Urban Vehicles，2008（7）：42.

［5］ 石得春.高速列车侧窗在交会压力波作用下的瞬态响应分析［J］.铁道车辆，2002，40（4）：71.SHI Dechun.The transient response analysis of side windows on high speed trains under the pressure wave of encountering another train［J］.Rolling Stock，2002，40（4）：71.

［6］ 王立闯，臧曙光，马眷荣，等.高速列车侧窗风压疲劳性能研究［J］.武汉理工大学学报，2010，32（22）：5.WANG Lichuang，ZANG Shuguang，MA Juanrong，et al.Fatigue loading capacities of side windows on high speed trains［J］.Journal of Wuhan University of Technology，2010，32（22）：5.

［7］ TAO Lili，DU Guangsheng，LIU Liping，et al.Experimental study and finite element analysis of wind-induced vibration of modal car based on fluid-structure interaction［J］.Journal of Hydrodynamics（B），2013，25（1）：118.

［8］ ADINA.Theory and modeling guide volumeⅢ：ADINA CFD＆FSI［M］.［S.l.］：ADINA R ＆D Inc.，2009.

［9］ Timmen L，Kolling S，Osterrieder P，et al.A finite element model for impact simulation with laminated glass ［J］.International Journal of Impact Engineering，2007，34（8）：1465.

［10］ European Committee for Standard.prEN13474-1：1999 Glass in building—design of glass panes—part 1：general basis of design［S］.London：British Standard Association，1999.

［11］ European Committee for Standard.prEN13474-2：2000 Glass in building—design of glass panes—part 2：design for uniformly distributed loads［S］.London：British Standard Association，2000.

［12］ 许骏，李一兵.基于风挡玻璃凹陷量的人车事故车速计算模型［J］，机械工程学报，2009，45（7）：210.XU Jun，LI Yibing.Pedestrian-vehicle accident impact speed calculation model based on windshield deflection［J］.Journal of Mechanical Engineering，2009，45（7）：210.