港口道路堆场水泥混凝土铺面荷载应力计算

周玉民，谈至明，胡洪龙，袁静波

（1.同济大学 道路与交通工程教育部重点实验室，上海201804；2.中交第四航务工程勘察设计院有限公司，广东 广州510230）

水泥混凝土铺面是港口道路、堆场铺面的重要形式.水泥混凝土铺面荷载应力计算是铺面设计的基础.Westergaard［1-4］根据稠密液体地基上无限大板或半无限大板假设，推导了三种荷载位置应力的解析计算式.Westergaard荷载应力解析计算式物理意义清楚、形式简明，但是，在应用于有限尺寸的水泥混凝土板荷载应力计算时受到限制，对于接缝传荷、多荷载构形以及基层超宽等的影响也不能考虑.20世纪70年代以来，有限元方法在铺面结构荷载应力计算中得到了快速的发展，开发了各种计算程序，可以考虑各种因素的影响，通过大量计算，回归得到水泥混凝土铺面荷载应力的近似计算式，但物理意义不清晰，适用范围受到限制.谈至明［5］依据Ressiner中厚板理论，采用有限元数值方法计算，考虑板尺寸、旁侧轮、旁侧轴等的影响，通过回归，得到临界荷位处的荷载应力近似计算式，提供了旁侧轮、旁侧轴影响系数诺模图，研究成果为我国现行《港口道路、堆场铺面设计与施工规范》（JTJ 296—96）［6］所采纳，上述分析基于单层板模型，未考虑基层超宽、接缝传荷以及层间接触条件的影响.随着航运事业的快速发展，今天，港口流动机械（集装箱卡车、装卸机械等）、集装箱荷载（堆放层数增加）和铺面结构组合均发生了较大的变化，表现为港口装卸机械日趋大型化、重型化，作业高密度化，过去流动机械荷载最大为400kN，如今港区流动机械荷载已有很大提高，有的流动机械支腿荷载已达5 800kN，集装箱堆场层数已达6，7层，箱脚接地压力从2.4MPa变化到最高超过12.0MPa之间［7］；同时，水泥混凝土铺面结构组合也有了新的发展，表现为整体刚度和承载力的增强.在这种新形势下，有必要深入分析港口流动机械、集装箱荷载作用下，水泥混凝土铺面最大荷载应力位置、大小的变化规律，研究提出物理意义清楚、简明的荷载应力计算式，用于港口道路、堆场水泥混凝土铺面的设计.

1 力学模型、荷载图式及临界荷位

1.1 力学模型

港口道路、堆场水泥混凝土铺面是由多种材料组合而成的层状结构体系，面板为有接缝的水泥混凝土板，基层通常采用刚性、半刚性材料（贫混凝土、碾压混凝土、水泥处治的碎（砾）石、石灰-粉煤灰碎（砾）石等），一般不设纵横缝，即基层平面尺寸通常较面板的大，是超宽的，基层之下为底基层或垫层.为了简化起见，其力学分析采用不等平面尺寸双层板模型［8］，假定各结构层材料是均匀、各向同性和线弹性的，面板与基层之间层间接触条件为竖向受压连续、受拉可脱开，水平无摩阻，地基采用 Winkler假设，力学模型如图1所示.图中，Ec、Eb为面板和基层的弹性模量，MPa；μc、μb为面板和基层材料的泊松比；hc、hb为面板和基层的厚度，m；k为地基的反应模量，MN·m-3；L，B分别为面板长和宽，m；La1，La2均为基层板长方向上的加长，m；Ba1，Ba2均为基层板宽方向上的加宽，m；P为单轮荷载，kN.

图1 不等平面尺寸双层板模型Fig.1 Unequal planar dimension double-layered concrete pavement model

1.2 荷载图式

1.3 临界荷位

水泥混凝土铺面最大荷载应力的位置和大小是随外部荷载作用位置的变化而改变的，在所有荷位对应的铺面结构最大荷载应力里面，又存在一个极大值，将该极大值对应的荷载作用位置称为临界荷位.分析表明，对于面板，流动机械荷载和集装箱荷载对应的临界荷位在纵缝边缘中部；对于基层，流动机械荷载对应的临界荷位有两个位置，即在板角隅或纵缝边缘中部，取决于基层是否设置与面板对应的横缝.如果不设横缝，则基层临界荷位在角隅；反之，在纵缝边缘中部.造成基层临界荷位不定的一个根本原因在于力学模型采用了线弹性假设，由此导致角隅荷位下基层应力的不收敛，若考虑到基层的塑性效应，基层的临界荷位仍在纵缝边缘中部，与面板的一致.集装箱荷载对应的临界荷位在纵缝边缘中部.

图2 港口道路、堆场水泥混凝土铺面荷载图式Fig.2 Load configurations for road and terminal concrete pavement of port areas

2 铺面结构荷载应力计算

2.1 一般荷载应力计算式

流动机械荷载、集装箱荷载作用于水泥混凝土铺面面板临界荷位（面板纵缝边缘中部），相应的铺面结构面板和基层荷载应力σ1、σ2一般计算式分别见式（1）和式（2）：

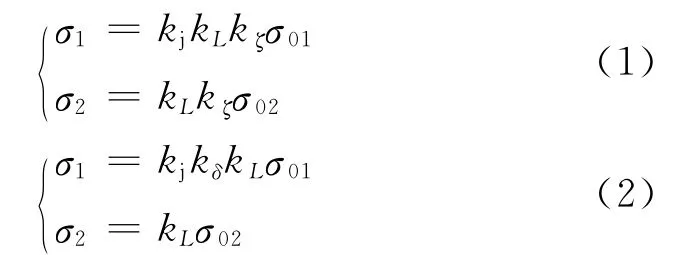
式（1）—（2）中：kj为基层超宽和接缝传荷对面板应力综合修正系数；kL为面板平面尺寸系数；kζ为旁侧轮修正系数；kδ为集装箱荷载作用下的面板应变非线性修正系数，单箱的计算见式（3），单列箱、多列箱的kδ=1；σ01、σ02为单轮（单箱、单列箱、多列箱）荷载作用于等平面尺寸无限大板临界荷位时面板、基层荷载应力.

单箱荷载作用下的面板应变非线性修正系数kδ为

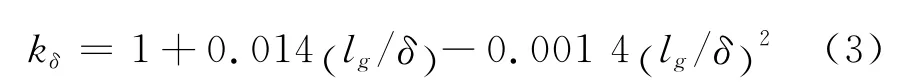
式中：δ为单轮（单箱）荷载接地面积的当量圆半径，δ=（S/π）0.5，其中，S 为荷载作用面积，单列箱、多列箱的δ=（2×0.178+c）/π0.5；lg为铺面结构总的相对刚度半径，lg=［（Gc+Gb）/k］0.25，其中，Gc，Gb为面板和基层抗弯刚度.

2.2 荷载应力σ01、σ02

基层与面板等平面尺寸，单轮（单箱、单列箱、多列箱）荷载作用于无限大板临界荷位，荷载应力σ01、σ02为：

这个时候，顾青的家里又发生了一件大事，他正在上高中的弟弟病了，神经炎，如果不及时治疗会有瘫痪的危险。温简知道顾青的父母都是微薄的收入，抚养两个孩子后更是没有积蓄，看着顾青为难的样子，她说寄钱给他们吧。

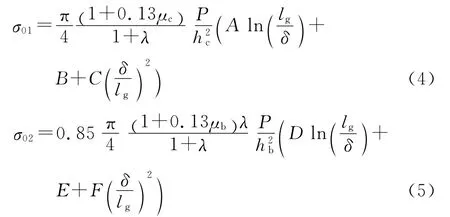
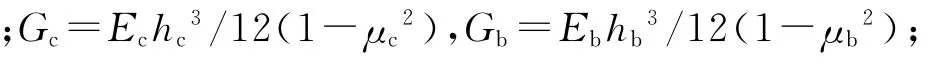
2.3 旁侧轮修正系数kζ

单轴荷载作用于面板临界荷位，旁侧轮对铺面结构荷载应力的影响可用一个旁侧轮系数ζ来表征（单轴荷载应力与单轮荷载应力之差除以单轮荷载应力），旁侧轮修正系数kζ为

图3所示为旁侧轮系数ζ与轮距d和总刚度半径lg之比d/lg的曲线图.经回归分析，旁侧轮系数ζ的近似计算式如下：

表1 回归系数 A、B、C、D、E、FTab.1 Regressed coefficients A，B，C，D，E，F

式中：A=1.34+0.02L/（lg+δ），B=0.6+0.06L/（lg+δ）.

式（7）的相对误差较小，绝大部分可控制在2%以内，最大不超过5%.

港口流动机械荷载轴间距一般变动在1.4～4.0 m之间，但一块板长通常是5m，单轴荷载作用于板纵缝边缘中部时荷载应力最大，在一块板内增加一根轴，轴间距不能超过半块板的长度，考虑到荷载接地轮印长度，轴间距变动在1.4～2.0m之间，否则另一根轴就落在相邻板上了.计算分析表明，同单轴荷载作用产生的荷载应力相比，多轴荷载（两轴在一块板上，或者三轴有两轴在一块板而另一轴在邻板上）在面板产生的应力是有所减小的.出于简化设计和保守的考虑，建议不考虑旁轴的影响.

2.4 面板平面尺寸修正系数kL

港口道路、堆场水泥混凝土铺面结构的荷载应力会随着面板平面尺寸的变化而改变.图4所示为水泥混凝土面板的平面尺寸系数kL（面板尺寸变化时面板（基层）最大荷载应力与无限大板（基层）最大荷载应力之比）随比值L/（lg+δ）变化的散点图.

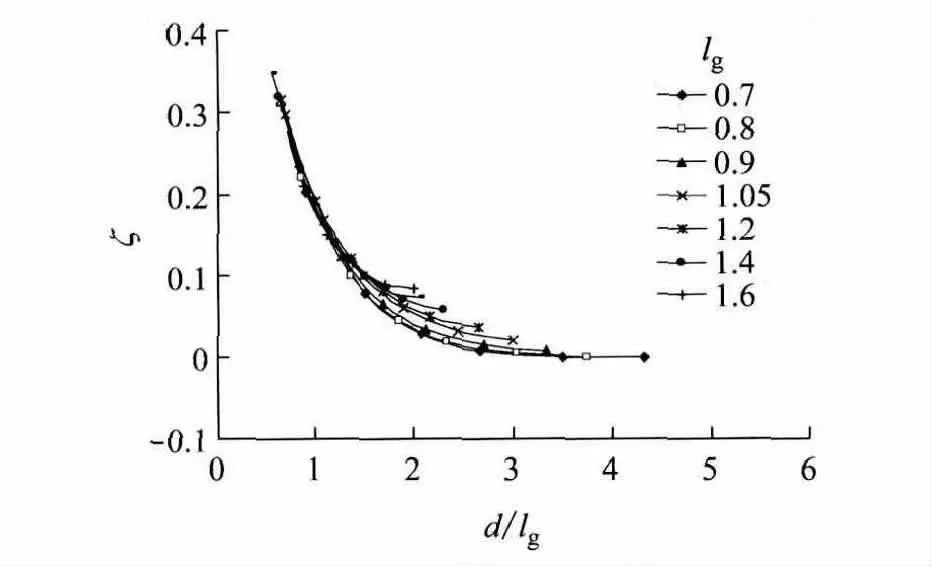
图3 ζ～d/lg曲线图Fig.3 Diagram ofζ～d/lgcurves

当L/（lg+δ）≤4时，面板平面尺寸系数kL单调变动在0.58～1.0之间；当L/（lg+δ）＞4时，面板平面尺寸系数稳定于1.面板平面尺寸系数kL的近似计算式如下：

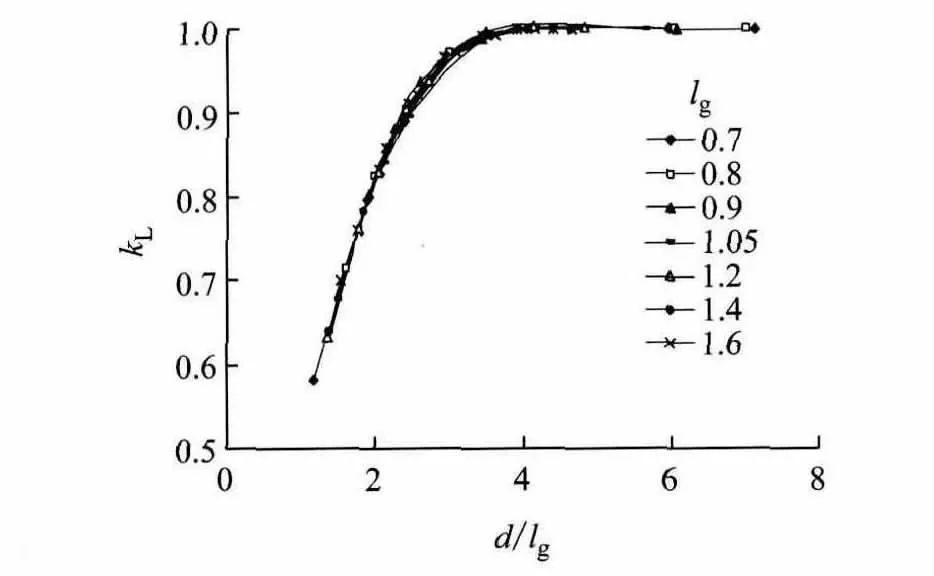
图4 kL～L/（lg＋δ）曲线图Fig.4 Diagram of kL～L/（lg＋δ）curves

2.5 基层超宽和接缝传荷综合修正系数kj

港口道路、堆场水泥混凝土铺面面板是有限尺寸的，基层除了材料弹性模量大于18 000MPa外，通常不设对应的纵、横缝，也就是说，基层平面尺寸较面板的大，基层是超宽的.同时，接缝处因集料嵌锁或设置传力杆、拉杆等而具有部分传荷的作用，考虑基层超宽和接缝传荷效应对面板荷载应力的影响，用一个综合修正系数kj表征：

式中：kjb为无接缝传荷时基层无限超宽引起的面板荷载应力折减系数；kjc为基层无限超宽时仅接缝传荷导致的面板荷载应力折减系数.

无接缝传荷，即接缝剪切刚度c=0，基层超宽应力折减系数kjb定义为基层无限超宽时面板的最大荷载应力σ1，∞同基层无超宽时面板最大荷载应力σ1，0的比值，计算如下：

基层无限超宽，仅接缝传荷导致的面板荷载应力折减系数kjc的计算式如下：

经统计回归，λ=0.02～0.2时，基层超宽应力折减系数kjb的近似计算式如下：

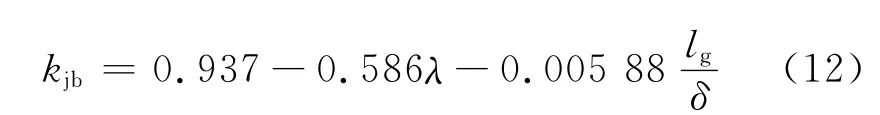
图5所示基层无限超宽时仅接缝传荷导致的面板荷载应力折减系数kjc随接缝剪切刚度c变化的曲线图.

图5 接缝传荷应力折减系数kjc-c曲线图Fig.5 Diagram of kjc-c curves

经回归分析，接缝剪切刚度c=1～10 000MPa·m-1时，面板荷载应力折减系数kjc近似式为

3 比较

图6所示为5m×5m等平面尺寸水泥混凝土铺面结构在单轮荷载作用于面板纵缝边缘中部时，有限元荷载应力σ1e，σ2e（横坐标）与式（2）荷载应力（纵坐标）的对比散点图.

从图6可以看到，对于面板荷载应力，除个别结构组合的相对差略微超出5%外，绝大多数结构组合的相对差均可控制在5%以内；对于基层荷载应力，相对差大部分可控制在5%以内，个别略超10%.显然，有限元结果和公式结果具有较好的一致性和精度.

图6 单轮荷载作用下5m×5m板荷载应力对比Fig.6 Comparison of loading stresses for 5m×5mslab under single wheel load

4 结论

通过对港口道路、堆场水泥混凝土铺面结构的荷载应力计算分析，总结如下：

（1）流动机械荷载作用下，有限尺寸水泥混凝土铺面结构临界荷位处荷载应力，可通过对单轮荷载作用下等平面尺寸大板荷载应力进行尺寸修正、旁侧轮修正以及基层超宽和接缝传荷综合修正后，采用式（1）计算.集装箱荷载作用下，可通过对等平面尺寸大板荷载应力进行尺寸修正，以及基层超宽和接缝传荷综合修正后，采用式（2）计算.

（2）旁侧轮对铺面结构荷载应力的影响可用旁侧轮系数ζ来表征，其计算见式（7），计算误差不超过5%.同单轴荷载作用产生的荷载应力相比，多轴荷载（两轴在一块板上，或者三轴有两轴在一块板而另一轴在邻板上）在面板产生的应力是有所减小的.出于简化设计和保守的考虑，建议不考虑旁轴的影响.

（3）当L/（lg+δ）≤4时，面板平面尺寸修正系数kL单调变动在0.58～1.0之间；当L/（lg+δ）＞4时，kL稳定于1，面板平面尺寸修正系数kL计算见式（8）.

（4）基层超宽和接缝传荷可降低面板荷载应力，其中，基层超宽的降低作用是显著的，而传力杆、拉杆传荷对面板荷载应力降低作用是次要的，基层超宽和接缝传荷对面板荷载应力综合修正系数计算见式（9）、（12）和（13）.

（5）流动机械、集装箱荷载作用下，5m×5m等平面尺寸水泥混凝土铺面结构荷载应力，对于面板，除个别结构组合的荷载应力相对差略微超出5%外，绝大多数结构组合的相对差均可控制在5%以内；对于基层，荷载应力相对差大部分可控制在5%以内，个别略超10%，有限元结果和公式结果具有较好的一致性和精度.

［1］ Westergaard H M.Stresses in concrete pavements computed by theoretical analysis［J］.Public Roads，1926，7（2）：25.

［2］ Westergaard H M.Analytical tools for judging results of structural tests of concrete pavements［J］.Public Roads，1933，14（10）：185.

［3］ Westergaard H M.Stresses in concrete runways of airports［C］//Proceedings of 19th Annual Meeting，Highway Research Board.Washington D C：Highway Research Board，1939：197-205.

［4］ Westergaard H M.New formulas for stresses in concrete pavements of airfields［J］.ASCE Transactions，1948，113：425.

［5］ 谈至明.港区刚性铺面结构的荷载应力［J］.水运工程，1997（4）：54.TAN Zhiming.Loads stresses of rigid pavement structure of ports［J］.Port and Waterway Engineering，1997（4）：54.

［6］ 中华人民共和国交通部.JTJ 296—96港口道路、堆场铺面设计与施工规范［S］.北京：人民交通出版社，1997.Ministry of Communications of the People’s Republic of China.JTJ 296—96 Technical code of road and stock yard pavement for the port area［S］.Beijing：China Communications Press，1997.

［7］ 中华人民共和国交通部.JTS 144—1—2010港口工程荷载规范［S］.北京：人民交通出版社，2012.Ministry of Communications of the People’s Republic of China.JTS 144—2010 Load code for harbour engineering［S］.Beijing：China Communications Press，2012.

［8］ 谈至明，周玉民，刘少文，等.不等尺寸双层混凝土路面结构力学模型研究［J］.工程力学，2010，27（3）：132.TAN Zhiming，ZHOU Yumin，LIU Shaowen，et al.A study on mechanistic model of double-layered concrete pavement structure with unequal planar dimensions［J］.Engineering Mechanics，2010，27（3）：132.