不同湍流模型在列车外流场计算中的比较

夏 超，单希壮，杨志刚，李启良

（同济大学 上海地面交通风洞中心，上海201804）

列车外流场绝大部分是高度非线性的湍流流动，目前工程上广泛采用Reynolds平均法对瞬时的湍流控制方程进行处理.但由于方程中多出了与脉动量有关的项-ρu-′iu-′j（Reynolds应力），研究者需通过对Reynolds应力作出某种假定，即引入新的湍流模型，来封闭方程组.目前常用的湍流模型有两大类：Reynolds应力模型和涡粘模型.Reynolds应力模型直接构建表示Reynolds应力的方程.涡粘模型是基于Boussinesq提出的涡粘假定，该假定建立了Reynolds应力相对于平均平均速度梯度的关系.依据确定涡粘系数μt的微分方程数目多少，涡粘模型包括：零方程模型、一方程模型和两方程模型，目前两方程模型得到了广泛应用.为书写方便，本文分别以SPA、SKE、RNG、RKE、SKW、SST和 RSM 分别表示Spalart-Allmaras、Standard（标准）k-ε、RNG（重整化群）k-ε、Realizable（可实现）k-ε、Standard（标准）k-w、SST（剪切应力输运）k-w和Reynolds stress（雷诺应力）湍流模型.

湍流模型的选取对于数值模拟的精度具有决定性的作用，在汽车和航空领域的外流场的数值模拟中，国内外研究者对常用的湍流模型的适用性进行了许多研究比较，Jones等［1］在翼型绕流中比较了RNG、RSM、V2F、SPA和SST模型的不同；杨胜等［2］采用SPA、SKE、RNG、RKE和 RSM 对汽车外部复杂漩涡绕流进行了数值模拟.大量研究表明［1，3］没有一种湍流模型能给出与试验结果完全一致的预测结果，因为每种湍流模型基于的各种假设和包含的经验常数都具有一定局限性，可能只适用于某些特定的情况.

Hucho［4］指出对于汽车尾部的分离可分为两类：准二维的分离和三维分离.而列车的外流场虽与汽车具有类似的特点，但由于列车尾部较细长，准二维的分离相对汽车来说会弱化，因此其外流场会与汽车外流场有一些不同.目前在列车外流场方面，研究者们通常是借鉴汽车和翼型外流场来选择湍流模型，其中SKE、RKE和RNG是国内外研究者常用的湍流模型，如 Cheli等［5］采用 RKE［6］进行列车外流场的计算.近年来研究者［7］开始将SST模型用于列车外流场的数值模拟，但是国内外针对不同湍流模型在列车外流场的模拟中的适用性的相关研究则较少.马静［8］比较了 RSM、SKE、RNG、RKE、SKW、SST和SPA模型在列车外流场模拟中的气动力的计算精度；张军海等［9］对比了SKE、RKE和RNG湍流模型在某高速列车外流场模拟中，模型表面压力和流场速度的不同.Christina等［10］对 SKE 和Quadratic（二次）k-ε模型在列车侧风工况下的适用性进行了研究.其中前两个研究评价湍流模型都没有试验结果的支撑，而且对于外流场中最重要的部分，即尾部的分离特征并没有进行研究比较，所以不同湍流模型在列车外流场的适用性还有待进一步的研究.本文通过对某简化缩比列车模型进行测力以及尾部的油流试验，评估了SKE、RNG、RKE、SKW和SST这5种常用的两方程湍流模型进行列车外流场数值模拟的精度，分析比较了5种湍流模型的优劣，通过这些研究可以为列车外流场数值计算方法的选择提供重要的指导.

1 湍流模型

1.1 两方程湍流模型

本文采用的5种两方程湍流模型中的这些常数或变量的具体取值可参考文献［11-16］.

1.2 壁面函数法

第1.1节中的湍流模型都是针对充分发展的湍流，是高雷诺数的湍流模型，只能用于求解湍流核心区的流动.而在壁面区，流动情况变化很大，特别是在粘性底层，流动几乎是层流，湍流应力几乎不起作用.壁面函数法是一组半经验公式，用于将壁面上的物理量与湍流核心区的求解变量联系起来.这样，不需要对壁面区内的流动进行求解，就可直接得到与壁面相邻控制体积的节点变量值［13］.

2 试验研究和数值模拟

2.1 试验方法

试验模型是利用Matlab和Catia采用参数化建模方法得到简化列车模型的几何外形，模型长550 mm，宽77mm，高90mm，阻塞度为5.6%，材质为工程塑料，喷亚光黑漆处理，如图1所示.

图1 简化列车模型Fig.1 Simplified train model

本次试验是在上海地面交通风洞中心1∶15的模型风洞中进行，该模型风洞为3/4开口式风洞，喷口面积为0.123m2，驻室长1.57m，宽1.185m，高0.818m，最高风速49m·s-1，模型区轴向静压梯度小于0.005m-1，喷口湍流度为0.6%.试验主要包括测力和油流试验.其中测力试验采用盒式六分力天平进行测量，分别进行20、30、40和45m·s-1四种工况测量.油流试验采用的配方为：二甲基硅油、二氧化钛和煤油的量分别为50、5和15mL.因为油流法是显示复杂流动的有效的手段，通过对表面油流谱的分析可以了解流体在表面发生转捩的位置、分离的位置、分离方式和特点、旋涡的形成等.所以本文采用油流法来研究模型尾部的分离特征.本次油流试验的工况为：45m·s-1风速，工程塑料材质的模型，持续吹风15min.

2.2 数值计算方法

本次数值仿真的工况及计算相关设置如下：

（1）模型风洞取主要部分作为计算域，其计算域及主要的边界条件的设置如图2所示，其中扩散段后边加了一段延长段，是防止出口有回流，延长段的四周壁面都设置为对称边界条件.采用六面体网格，边界层第一层网格厚度为0.5mm，增长率为1.05，对模型尾部进行加密，模型网格如图3所示.

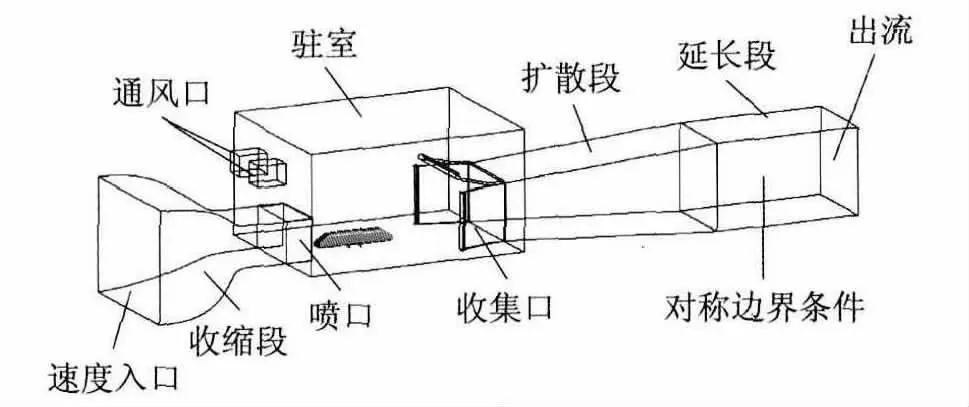
图2 计算域及边界条件Fig.2 Computational domain and boundary conditions

图3 模型周围网格Fig.3 Mesh around the model

（2）采用SKE、RNG、RKE、SKW 和SST这5种不同湍流模型分别进行求解，为了对5种湍流模型在相同网格数量下进行比较，本文保证第一层网格厚度一致，都采用非平衡壁面函数，y+（第一层网格尺寸的量纲一化量）满足30～80.其中需要特别说明的是SKW和SST模型的近壁面处理方法，文献［15］指出SKW和SST模型可以根据第一层网格厚度自动在壁面函数和低雷诺数处理近壁面之间进行转换.对流项和扩散项都采用二阶离散格式，压力速度耦合方式采用Simple算法.

2.3 网格无关性

数值计算的结果的准确性很大程度上取决于网格的数量和质量，所以本文首先针对网格数量无关性进行了研究，并保证网格质量都在同一水平，通过改变模型表面和周围网格的大小来确定最优的网格数.因为本文比较的湍流模型都采用非平衡壁面函数，所以保持边界层网格不变.定义网格无关性标准差：

式中：Xi为阻力系数Cd；σ为第i次之后所有Xi的标准差；n为次数.

表1给出了网格无关性的研究结果，当网格数超过677万后，无关性标准差σ≤0.002，可知对于解决工程问题，数值计算结果已满足要求，所以可以确定选取677万作为数值计算的网格数.

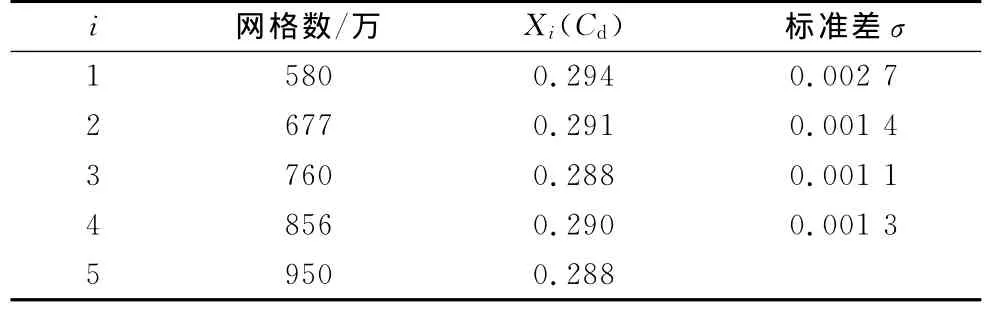
表1 网格无关性研究结果Tab.1 Results of grid independence

3 试验与数值计算结果的分析

3.1 气动力系数的比较

表2显示了5种湍流模型计算的列车模型不同风速V下的阻力系数Cd和升力系数Cl与试验值的比较.从表中结果可以看出，阻力系数Cd都随着速度增加而逐渐减小，升力系数Cl变化较小.这是因为随着雷诺数的增加，湍流边界层能够抵抗较高的逆压梯度，模型尾部分离点的位置向下移动，使得尾迹区域的宽度变窄，压差阻力逐渐减小，因而阻力系数逐渐减小，而对升力方向的影响不大.对于阻力系数Cd来说，与试验值相比，RKE、RNG和SST的计算结果较为精确，误差都在10%以内.其中RKE的计算结果最为精确，不同风速下的误差都在5%以下，最小为2.5%；而计算精度较差的是SKE和SKW.对于升力系数Cl来说，与试验值相比，RKE和SST的计算结果较为精确，误差基本都在10%以内.其中SST的计算结果最为精确，不同风速下的误差都在3%以下，最小为0.5%；而SKE和RNG的计算精度较差.

综上可知：RKE和SST对阻力和升力的预测都比较精确，而SKE和SKW则对阻力和升力的预测精度较差.分析原因如下：

（1）SKE假定涡粘系数μt是各向同性的标量，所以其用于弯曲壁面流动、涡旋流动的流动时，会产生一定的失真.通常SKE会高估滞止区的湍流度而造成滞止区范围较大，预测阻力偏大，本文研究中SKE计算的Cd值比试验值高了16.7%～26%.RKE弥补了 k-ε 中存在的两大缺陷［6，12-13］：一个是对应变率特别大的情形，k-ε方程可能导致负的正应力，所以对正应力进行了某种数学约束；另一个是在涡粘系数的计算公式中，系数Cμ不应是常数而应该是与旋转应变率有关的量.所以RKE在用于列车外流场这种带有边界层流动以及漩涡大分离的流动中计算精度较高.本文RKE模型计算的Cd值与试验的误差都在5%以内.

（2）SKW模型虽然计及了近壁面处剪切流动的传播，提高了对压力梯度的灵敏度，但其求解结果对来流条件的k和w非常敏感.而从表2可以看到不同风速下，SKW预测的阻力系数Cd与试验的误差最小为22.1%，最大为36.6%；升力系数Cl与试验的误差最小为-4.3%，最大为-17.4%.而SST则是通过一个混合函数将SKE和SKW相结合而成的模型［11，15］，它在近壁面处使用SKW，而在边界层外和自由流区使用SKE模型，在混合区内则通过混合函数F混合使用两个模型，这样使得SST在模拟一些分离流动方面都比SKW精度更高更可靠.在本文研究的列车外流场计算中，SST对升力系数Cl的计算精度较好，与试验结果的误差都在3%以内，对阻力系数Cd的计算精度不如RKE模型，但误差都在10%以内.

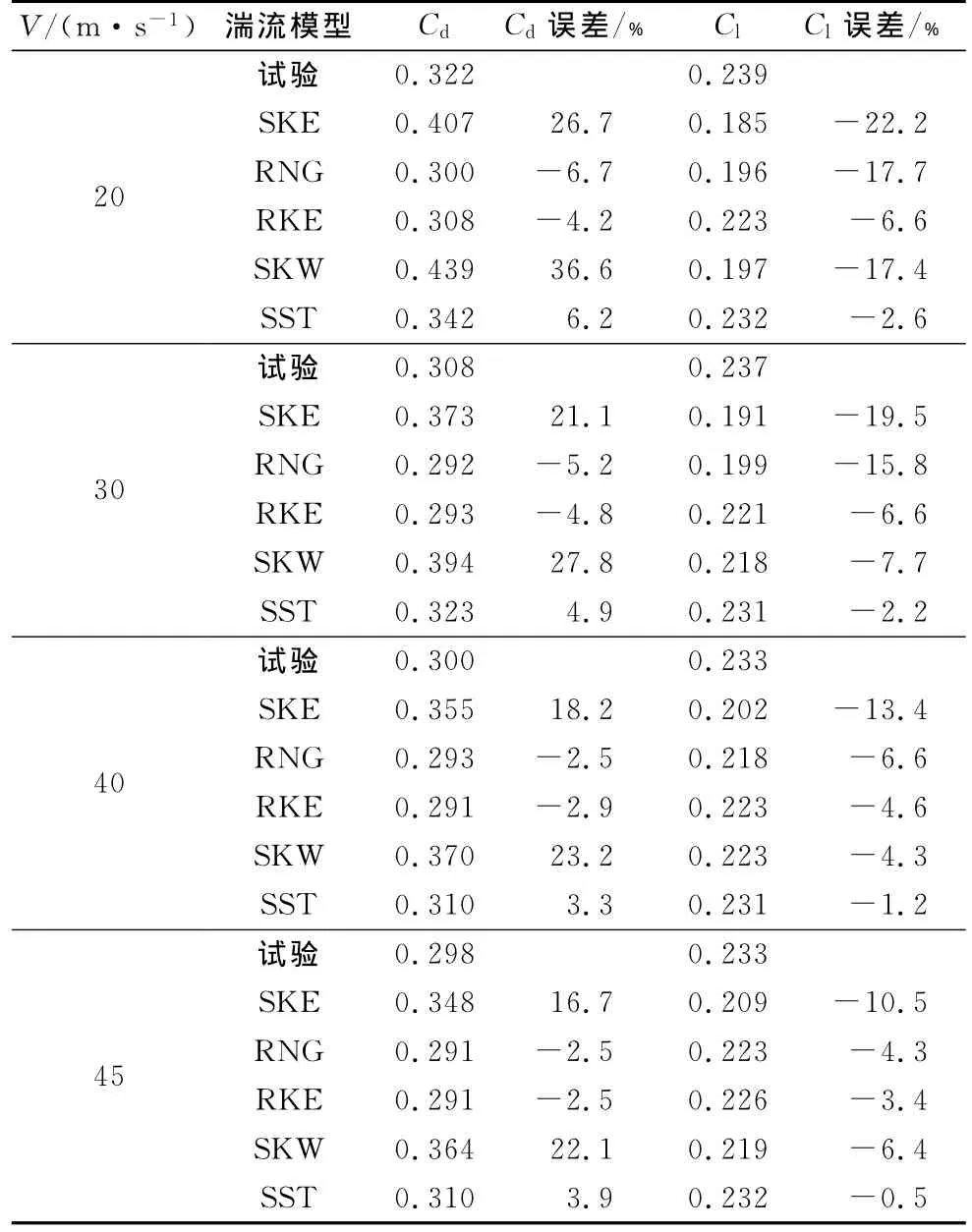
表2 气动力系数的数值模拟与试验结果对比Tab.2 Comparison between numerical simulation and test result on aerodynamic coefficients

3.2 尾部油流谱的比较

图4给出了试验得到的尾部油流谱，包括分离线，分离螺旋点和再附线.其中分离线特点为周围质点都向此处运动，这样示踪粒子都在此堆积，形成白线；分离螺旋点特点就是周围质点都向螺旋点运动，旋成涡旋状，造成示踪粒子堆积；再附线特点是周围质点运动方向都背离该线，所以没有示踪粒子的堆积.

具体分析其油流谱可以看到：在图4a中，模型顶部出现了少量示踪粒子堆积，说明此处气流出现了微弱的分离，而这种分离是由于逆压梯度作用而形成，类似于熟悉的翼型尾部的分离，这里称为分离一；从图4a和4b可以看到：在模型的背部和侧部有明显的“人”字形分离线和一对分离螺旋点，此处的分离是因为背部的气流和侧部、底部翻转上来的气流在此处汇聚，继而发生旋转形成一对对称的拖曳涡脱离模型而造成的，这里称为分离二；从图4c可以看到模型最尾端同时出现有分离线和再附线，这里的分离同分离二类似，由于逆压梯度作用，使气流分离形成漩涡，随后漩涡再附到模型上而形成的，模型尾端的上部和下部分别有一个漩涡形成，这里称为分离三.分离一和分离三就是前言中提到的准二维分离，而分离二就是指三维的分离.

图5和图6显示数值模拟的5种湍流模型的尾部油流谱，图例表示表面剪切应力的大小，剪切应力为零的地方就是出现分离的部位.从图6中可以看到：SKW和SST预测到了因逆压梯度造成的分离一，但和试验相比，其预测的分离区过大，这与Wilcox［16］指出k-w模型有对分离区预测过大的特点相一致.分析原因为SST和SKW模型都计及了近壁面处的低雷诺数效应和剪切流动的传播，提高了对压力梯度的灵敏度.而其余模型均没有预测到此处的分离，但可以看到RKE在此处附近的剪切应力相对SKE和RNG要小，说明RKE预测相对较准确.

从图5和图6中可以得到：对于分离二，SKE和RKE预测较为准确，其中以RKE预测的分离线和分离螺旋点的位置与试验最为接近.因为SKE通常高估湍流剪切应力，这样就会导致分离推迟，从图6可看到SKE预测的分离区小于RKE和试验结果.RNG模型对分离螺旋点的预测较差，而SKW和SST对分离二的预测和试验相差较大.分析原因为RKE中涡粘系数μt的计算公式中系数Cμ考虑了与旋转应变率有关的量，所以对涡旋流动模拟较准确.而RNG、KWS和SST在模拟复杂流线和带有强烈旋涡，旋转应变的流场时，精度不高.这是因为RNG和KWS中的涡粘系数μt中的系数Cμ是个经验常数，可能只适应某些流场.而第3.1节中已提到SST是通过一个混合函数将SKE和SKW相结合而成的模型，它在近壁面处使用SKW，而在边界层外和自由流区使用SKE模型，所以其在模拟复杂流线和带有强烈旋涡时也会存在与SKW和SKE类似的特点.同时为克服SST模型中的涡粘系数μt会存在奇异解这一缺陷，模型对涡粘系数μt作了一定的限制，而限制中的常数因采用了一些经验和试验的数据，可能在某些特定流场计算下有效.

从图5可以看到：对于分离三，5种模型都较准确地捕捉到了.

图4 尾部试验油流谱Fig.4 Oil streamline on tail by test

图5 尾部数值模拟的剪切应力油流谱（后视图）Fig.5 Oil streamline of wall shear on tail by numerical simulation（rear view）

图6 尾部数值模拟的剪切应力油流谱（侧视图）Fig.6 Oil streamline of wall shear on tail by numerical simulation （lateral view）

4 结论

通过对简化列车模型进行外流场的数值模拟和风洞试验，比较了5种湍流模型的计算精度，结果表明：

（1）RKE和SST模型对阻力和升力的预测都相对准确，其中RKE在阻力的计算上精度最高，误差都在5%以内；SST在升力的计算上最为精确，误差在3%以内.而SKE和SKW则在阻力的计算上表现较差，误差在15%以上；SKE和RNG则在升力的计算上精度较差，误差基本都在10%以上.RKE通过对正应力进行了某种数学约束，并在涡粘系数中引入与旋转应变率有关的量，提高了k-ε对列车阻力的数值模拟精度.

（2）SKW和SST模型都考虑了近壁面处的低雷诺数效应和剪切流动的传播，所以对因逆压梯度造成的分离一预测较准确，但预测的分离区通常过大；而SKE和RNG这两种k-ε模型对于逆压梯度造成的分离一都预测较差，RKE预测相对准确.而SKW、SST以及RNG对于因气流交汇形成拖曳涡而造成的分离二预测准度较差，主要是因为其涡粘系数μt的计算公式中系数Cμ是经验常数或是根据经验和试验的数据作了一定的限制，可能在某些特定流场计算下有效，而对于列车的尾部复杂漩涡流场模拟精度不高.RKE模型中的涡粘系数μt因为引入了与旋转和曲率相关的内容，所以对分离二预测较准确.SKE也基本预测到了分离二，但是因为SKE通常高估湍流剪切应力，这样就会导致分离推迟，分离区小于真实值或不发生分离.综上可知，SKW和SST对准二维分离捕捉相对准确；RKE则对三维分离捕捉得更准确.

（3）通过以上气动力和分离特征的分析，RKE和SST湍流模型对于列车外流场的计算各有优劣，所以可以考虑将RKE和SST湍流模型结合起来，通过考虑旋转和曲率影响对SST模型中的SKE模型进行改进，以用来列车外流场的计算，期望可以取得更好的模拟精度，当然这还有待进一步的研究和验证.

［1］ Jones D A，Clark D B.Simulation of a wing-body junction experiment using the fluent code［J］.International Journal of Fluid Mechanics Research，2005（6）：26.

［2］ 杨胜，张扬军，涂尚荣，等.汽车外部复杂流场计算的湍流模型比较［J］.汽车工程，2003，25（4）：322.YANG Sheng，ZHANG Yangjun，TU Shangrong，et al.Comparison of different turbulence models for computation of complex flow around automobile［J］.Automotive Engineering，2003，25（4）：322.

［3］ 陶文铨.数值传热学［M］.2版.西安：西安交通大学出版社，2001.TAO Wenquan.Numerical heat transfer［M］.2nd ed.Xi’an：Xi’an Jiaotong University Press，2001.

［4］ Hucho W H.Aerodynamics of road vehicles［M］.4th ed.Warrendale：SAE Int，1998.

［5］ Cheli F，Ripamonti F，Rocchi D，et al.Aerodynamic behaviour investigation of the new EMUV250 train to cross wind［J］.Journal of Wind Engineering and Industrial Aerodynamics，2010，98（4/5）：189.

［6］ Shih T H，Liou W W，Shabbir A，et al.A new k-ε eddy viscosity model for high Reynolds number turbulent flows：model development and validation［J］.Computers and Fluids，1995，24（3）：227.

［7］ 孙振旭，郭迪龙，姚远，等.高速列车地面效应数值模拟研究［J］.计算物理，2013（1）：61.SUN Zhenxu，GUO Dilong，YAO Yuan，et al.Numerical study on ground effect of high speed trains［J］.Chinese Journal of Computational Physics，2013（1）：61.

［8］ 马静.横风下高速列车空气动力特性及其对行驶安全性影响研究［D］.上海：同济大学，2008.MA Jing.Study on the aerodynamic characteristics of high speed train under cross wind and its effect to the operating safety［D］.Shanghai：Tongji University，2008.

［9］ 张军海，王吉桥，吴向东，等.高速列车湍流特性的数值模拟［J］.铁道机车车辆，2010，30（1）：11.ZHANG Junhai，WANG Jiqiao， WU Xiangdong，et al.Numerical simulation on characteristics of turbulence flow around a high-speed train［J］.Railway Locomotive ＆Car，2010，30（1）：11.

［10］ Christina R，Thomas R，Dong W.Computational modeling of cross-wind stability of high-speed trains［C］∥ European Congress on Computational Methods in Applied Sciences and Engineering.Jyvaskyla：［s.n.］，2004：1-20.

［11］ Menter F R.Two-equation eddy-viscosity turbulence models for engineering applications［J］.AIAA Journal，1994，32（8）：1598.

［12］ Versteeg H K， Malalasekera W.An introduction to computational fluid dynamics：The finite volume method［M］.2nd ed.London：Prentice Hall，2007.

［13］ 王福军.计算流体动力学分析：CFD软件原理与应用［M］.北京：清华大学出版社，2004.WANG Fujun.Analysis computational fluid dynamics：theory and application of CFD software［M］.Beijing：Tsinghua University Press，2004.

［14］ Catalano P，Amato M.An evaluation of RANS turbulence modelling for aerodynamic applications［J］.Aerospace Science and Technology，2003，7（7）：493.

［15］ Menter F R，Kuntz M，Langtry R.Ten years of industrial experience with the SST turbulence model［J］.Turbulence，Heat and Mass Transfer，2003（4）：625.

［16］ Wilcox D C.Formulation of the k-ω turbulence model revisited［J］.AIAA Journal，2008，46（11）：2823.