类车体流固耦合现象实验及数值分析

朱 晖，杨志刚

（1.上海地面交通工具风洞中心，上海201804；2.上海市地面交通工具空气动力与热环境模拟重点实验室，上海201804）

侧风对车辆行驶安全性影响显著，是汽车空气动力学和系统动力学分析必须面对的难题［1］.尤其在高速工况下，侧风引起气动力/力矩激变，并伴随风压中心飘移现象，从而恶化汽车操纵稳定性和安全性［2］.

目前针对汽车在侧风环境中运动特性的研究多采用单纯空气动力学或多体动力学方法［3-5］，或采用分步协同的技术手段将二者结合［2，6］，极少考虑由侧风引起的车辆悬架形变和悬挂质量侧倾对车体所受气动力的影响.即在车辆侧风安全性研究中未能引入流固耦合机制.

类车体（Ahmed body）模型在1984年被引入［7］，由于其构造简单（无悬架结构）且其外流场具有三维、非稳态、近地面的特点，从而迅速成为研究车辆空气动力学的重要模型之一［1］.

本文以改进的类车体（简易悬架）为研究对象，在模型风洞中对其进行侧向吹风实验以获得车体位移数据；采用已证明有效性的流固耦合计算方法对改进类车体车身位移及外流场信息进行解算，揭示车体与流场相互作用的内在机制，并明确由此所引起的气动力变化规律.

1 改进的类车体模型及安装方式

经典的类车体模型由于底部支撑不具备弹性特征所以无法被引入流固耦合现象的研究中，其结构如图1所示.图中，l为车长，h为车高，g为支撑高，d为支撑直径，R为前端倒圆半径，S为斜面长度，α的后倾角.为此设计相应的具有弹簧的支撑附件并将其与类车体模型相接，从而形成简易的悬架结构，附件构造如图2所示.

本次实验台架为同济大学地面交通工具风洞中心1/15缩比空气动力学模型风洞，为满足风洞实验阻塞比的要求，制作了1/4基本类车体模型并将后倾角固定为25°.同时为实现车模及附件在风洞中的安装，设计制作了安装地板，如图3所示.

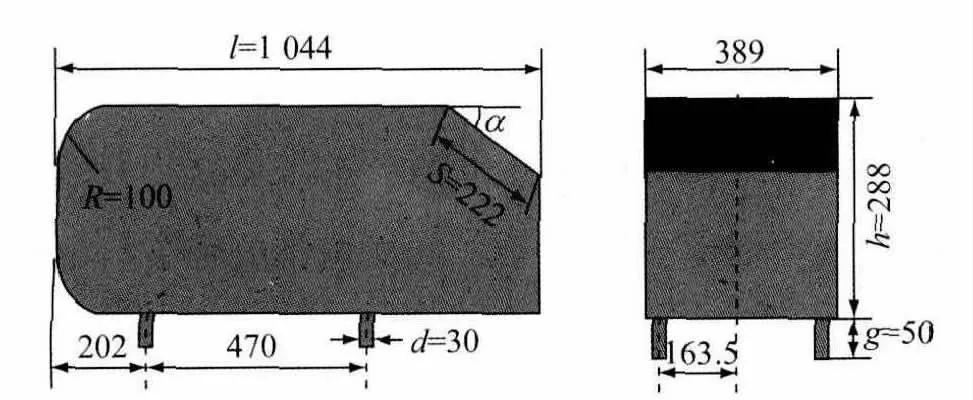
图1 类车体构造（单位：mm）Fig.1 Structure of Ahmed body（unit：mm）

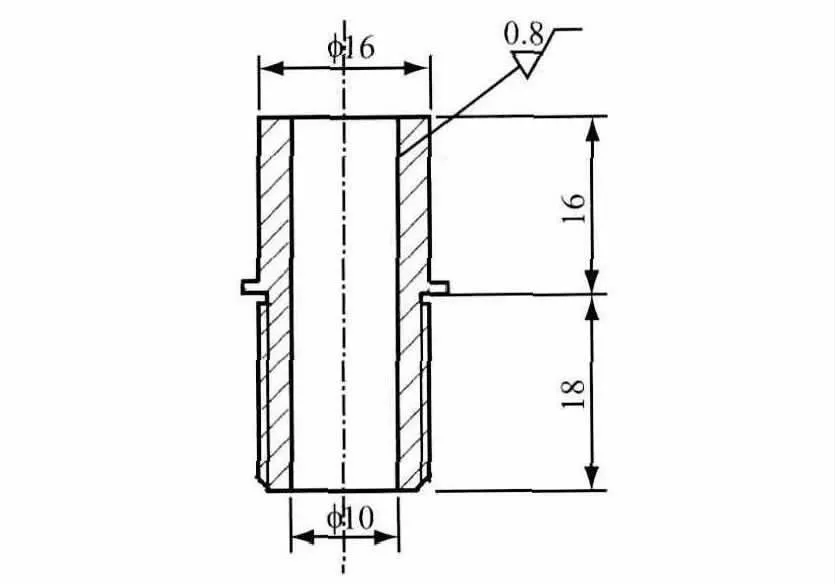
图2 附件结构（单位：mm）Fig.2 Structure of accessory（unit：mm）

图3 地板尺寸（单位：mm）Fig.3 Dimensions of floor system（unit：mm）

地板设计的尺寸与台架匹配，前段伸入喷口并倒圆角以减弱地板前缘对气流的扰动.地板、缩比车体及附件在缩比风洞中的相对关系及安装位置如图4所示.车体与喷口成90°夹角以使侧风效应最大化，同时为降低铜套内壁与弹簧之间摩擦力，使用润滑油对其实施润滑.

实验中采用固定位置的长焦镜头（等效距约202 mm）记录车体位置，并测量车体底部与风洞地板的夹角，作为实验的主要测量值并作为验证仿真方法有效性的基准，具体数据在后文给出.

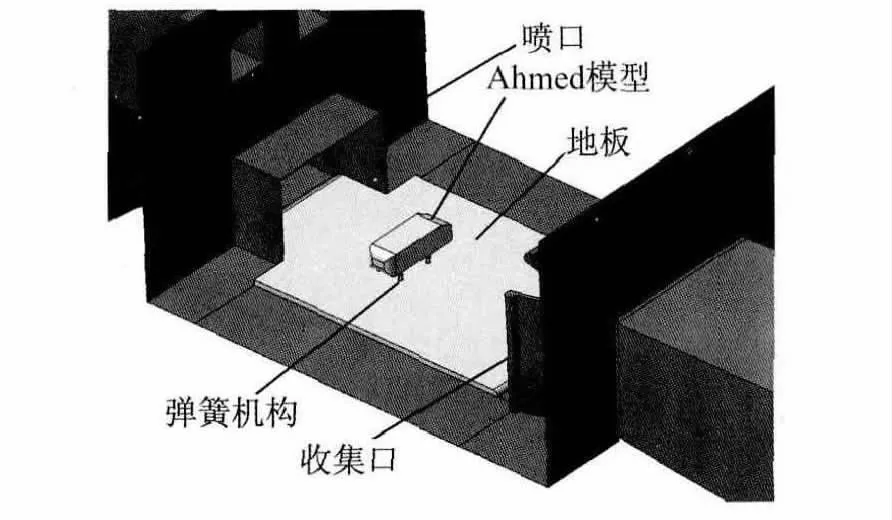
图4 总体布置及构件图Fig.4 Arrangement and assembly diagram

2 流固耦合仿真方法

风洞实验难以对流场的整体结构及细部特征进行描述和测量，因此必须采用数值仿真研究方法对流场进行全局解算.

有别于传统的外部绕流仿真方法（通常在全局坐标系中固体静止，且在当地坐标系中固体表面无形变），流固耦合仿真同时对固体及流体动力学参数进行解算，从而分析固体运动和流动之间的相互响应［8］.

为保证仿真与实验的空间一致性，参照缩比风洞结构及类车体安装方式，构建计算域如图5所显示.

图5 计算域结构Fig.5 Structure of computational domain

采用值域［2mm，200mm］的三角形网格对计算域各表面进行划分；采用四面体网格对计算域空间进行离散，对包含类车体模型在内的结构细节进行局部网格加密.与传统计算流体动力学（CFD）方法只划分流体区域网格不同，流固耦合现象的分析涉及流体和固体两大区域，所以类车体本身必须进行体网格的划分.

固体区和流体区面网格如图6所示，流场部分体网格数约200万单元，固体部分约4万单元.

流固耦合仿真涉及流体分析和结构分析两部分，流体分析采用任意Lagrange-Euler耦合有限体积法［9］，结构分析采用经典有限元法.分析流程从流场解算开始，两部分交替求解，如图7所示.图中Pn、Pn+1为第n、n+1步压力；Un、Un+1为第n、n+1步速度.

图6 面网格分布Fig.6 Distribution of surface mesh

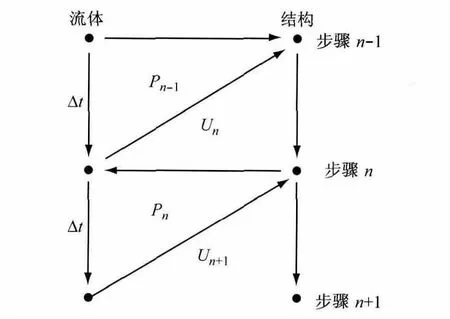
图7 耦合求解迭代格式Fig.7 Iteration algorithm of FSI

结构表面位移参数与流场壁面压力参数分别通过界面保形插值和守恒型插值方法传递［10］，传递松弛因子为0.8.由于耦合计算前后流场计算域的几何关系拓扑同胚且变形量有限，所以采用弹簧近似光顺模型实施动网格操作［11］，网格弹性系数为0.6、边界点松弛因子为0.5，每次流固界面传递参数迭代110次，以获得较好的网格质量.

流体仿真采用可实现K-ε湍流模型（Realizable K-ε Model）［12］.与传统K-ε 湍流模型相比，该湍流模型引入湍流粘度变化公式（不是常数），并为耗散率增加了新的传输方程，所以对旋转流动、强逆压梯度的边界层流动、流动分离和二次流有很好的表现.

边界条件见表1.进口采用速度进口，x方向速度U为20～40m·s-1，y及z方向速度V、W 皆为0m·s-1，湍流强度0.3%，与风洞实际流场品质一致；出口采用压力出口；压力平衡口采用进气口边界条件；车体表面为无滑移边界条件；其他构造皆采用固定壁面边界.采用非平衡壁面函数对近壁面流场进行求解.

表1 边界条件Tab.1 Boundary conditions

结构部分参考汽车系统动力学的四自由度模型，基于非线性轮胎力概念，利用拉格朗日能量法解算包括俯仰、侧倾、侧向、横摆4个自由度的运动方式，如图8所示，图中M、K、C分别表示质量、刚度、阻尼.模型底部由4个弹性系数均为3 921N·m-1的弹簧作为支撑，支撑长度为20mm，其余部分看作刚体，总重为705g.

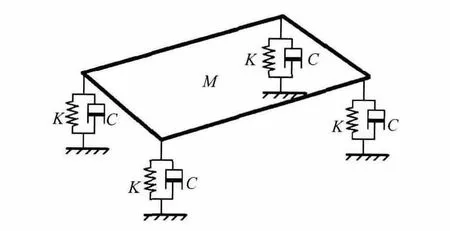
图8 四自由度系统动力学模型Fig.8 Four-freedom model of system dynamics

3 风洞试验及CFD分析结果

本次风洞试验的目的：形成关于具有简易悬架的类车体在横风作用下车身姿态的感性认知，测量类车体车身倾斜的角度，为流固耦合仿真分析提供数据支撑.由于模型风洞及类车体模型的尺寸较小，为防止测量器材部件对流场的干扰，实验中结合摄像技术对车体倾斜角度进行测量.

图9显示了风速20，40m·s-1时实验照片和数值解算截图，二者皆捕捉到车体侧倾现象，且趋势一致.

图10显示了横风环境中车体底部与风洞地板间夹角的实验结果与仿真数值，由图可知：随着风速（流场核心区平均风速）的提高，车体底部与地板间夹角几乎成线性增大，表明随着侧倾力矩的增大，车身倾斜程度增加；数值计算结果与风洞实验值之间的误差基本控制在5%以内，少数点在7%左右.

图9 车体侧倾现象Fig.9 Rolling phenomenon of Ahmed body

图10 类车体变形角度Fig.10 Deformation angle of Ahmed body

由图10可知：数值结果普遍大于实验值，且符合很好，中端数据略有偏差.原因为：由于简易悬架机构中的铜套与弹簧之间不可避免地存在接触摩阻（虽然已进行润滑处理），该摩阻妨碍了变形的发展；在横风风速较小时变形不明显摩阻较小，随着风速逐步增加，在变形量增加的同时摩阻亦增加，当风速进一步提高后，由于风载荷克服摩阻的作用使得数值结果与实验值又趋于一致.

图11显示了考虑流固耦合机制与否对气动力/力矩的影响，图中数据为以未考虑流固耦合机制数据为准，二者之间的相对差异.

图11 气动力、力矩差异Fig.11 Error of aerodynamic force and moment

由于车身在风载荷下会产生侧倾，车体姿态的改变导致流场涡结构的变化，如图12所示.车体的顶部流场结构的改变是造成升力明显变化的主要原因，由图12可知：计及流固耦合效应时顶部附体涡结构更为复杂，且车身变形造成顶部分离泡尺度明显大于不计流固耦合时的情况，且该附体涡的强度更高，导致车顶压力较低，气动升力更大.由于受车顶分离泡结构改变的影响，计及流固耦合效应时车后尾迹流的影响区域更广，且涡强度更高.

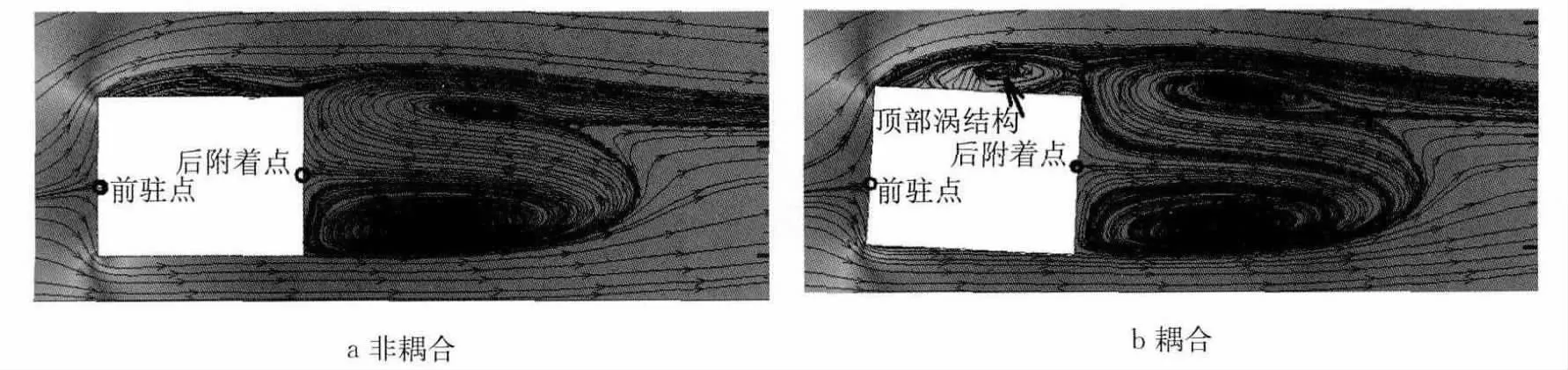
图12 纵截面流线图Fig.12 Streamline of longitudinal section

涡结构的再附着对壁面压力的分布影响突出，图13比较了计及流固耦合效应与否时流场在模型顶部型面上再附着情况.不计耦合效应时，车体顶面没有显著的再附着现象，流动顺畅平稳，压力变化较均匀；而计及耦合时顶面再附着明显（与图12所述的分离泡和顶部流场结构吻合），这导致车体顶面压力变化更剧烈，产生的气动力矩同时增大.

图13 车体油流图Fig.13 Oil streamline of Ahmed body

图14显示了车体侧倾对顶部压力分布的影响（对云图的分离噪点做了少量后期处理）：计及流固耦合效应时顶面低压区面积更大，整体压力更低，导致车体气动升力增加；且顶面压力沿纵向和横向分布都更不均匀，导致车体气动力矩增加，故而加重失稳趋势.

图14 车顶压力分布Fig.14 Pressure distribution of model top

流体前后附着点位置的变化主要影响模型的气动力矩，为了消除车体变形影响，表2采用了前后附着点对于车体的相对高度进行比较（相对高度：该点相对于几何位置的所在高度）.由表2可知：两者计算的后附着点高度差大于前驻点高度差，即耦合计算的后附着点较非耦合计算有明显提升，说明耦合计算的车体周围的速度环量大于非耦合计算的结果，进一步解释了耦合计算所得升力及气动转矩皆较高的原因.

表2 前后驻点相对位置Tab.2 Front and back stagnation point position

4 结论

通过对具备简易悬架结构的1/4类车体风洞实验及流固耦合仿真，得到以下结论：

（1）流固耦合效应主要影响车辆的气动升力及力矩；

（2）流固耦合效应对车体顶部及尾迹区流场结构及涡运动特征影响显著；

（3）从操控稳定性及安全性的角度出发，传统的试验测量及流动仿真结果偏安全，应引入流固耦合效应；

（4）文中涉及的流固耦合仿真方法可靠，可用于车辆气动性能预测评估.

［1］ Hucho W H.Aerodynamics of road vehicles［M］.4th ed.Detroit：SAE World Congress ＆Exhibition，2004.

［2］ 谷正气，王和毅，罗荣锋.计及风压中心漂移的汽车侧风稳定性研究［J］.湖南大学学报：自然科学版，2005，32（3）：70.GU Zhengqi，WANG Heyi，LUO Rongfeng.Study on automobile cross-wind stability in consideration of pressure center’s shift ［J］.Journa1 of Hunan University：Natural Sciences，2005，32（3）：70.

［3］ 王夫亮，傅立敏.侧风对轿车气动特性影响的数值模拟研究［J］.哈尔滨工业大学报，2006，38（8）：1255.WANG Fuliang，FU Limin.Numerical simulation of the crosswind effects on the aerodynamic performance of a sedan［J］.Journal of Harbin Institute of Technology，2006，38（8）：1255.

［4］ Coleman S A，Baker C J.High sided road vehicles in cross winds ［J］.Journal of Wind Engineering and Industrial Aerodynamics，1990，36：1383.

［5］ Tran V T.Crosswind feed forward control—a measure to improve vehicle crosswind behavior ［J］.Vehicle System Dynamics，1994，23（1）：165.

［6］ 海贵春，谷正气，王和毅.侧风对汽车高速行驶性能影响的仿真研究［J］.湖南大学学报：自然科学版，2006，33（2）：40.HAI Guichun，GU Zhengqi，WANG Heyi.Research on the effect of crosswinds on the stability of high speed vehicles［J］.Journal of Hunan University：Natural Sciences，2006，33（2）：40.

［7］ Ahmed S R，Ramm R，Faltin G.Some salient features of the time-averaged ground vehicle wake［C］//SAE.Detroit：SAE，1984：84-03-00.

［8］ 白象忠，郝亚娟.非线性流体弹力学研究进展［J］.力学进展，2008，38（5）：545.BAI Xiangzhong， HAO Yajuan.Advances in nonlinear hydroelasticity［J］.Advances in Mechanics，2008，38（5）：545.

［9］ Hirt C W，Amsden A，Cook J L.An arbitrary Lagrangian-Eulerian computing method for all flow speeds［J］.Journal of Computational Physics，1974，14：76.

［10］ Dukowicz J K，Kodis J W.Accurate conservative remapping（rezoning）for arbitrary Lagrangian-Eulerian computations［J］.Journal of Computational Physics，1987，8（3）：305.

［11］ Degand C，Farhat C.A three-dimensional torsional spring analogy method for unstructured dynamic meshes ［J］.Computers and Structures，2002，80：305.

［12］ Shih T H，Liou W W，Shabbir A，et al.A new k-e eddy viscosity model for high Reynolds number turbulent flowsmodel development and validation ［J］.Computer and Fluids，1995，24（3）：227.