线夹回转式导线阻尼间隔棒防舞机理与模态分析

刘连光，赵强，刘自发，葛江锋，姚建生，仇坚，朱小强

(1.华北电力大学电气与电子工程学院，北京市102206;2.江苏天南电力器材有限公司，江苏省如皋市226522)

0 引言

分裂导线阻尼间隔棒是分裂导线输电线路的主要防保金具之一，对子导线起夹持支撑以及防止导线微风振动等作用。利用线夹回转式间隔棒防御舞动是日本首先提出，并进行研究、实验和应用［1-4］的。其中，文献［1］介绍了日本多次发生的输电线路冰雪舞动灾害事故，包括2005年12月22日，发生在日本新潟下越地区的覆冰事故造成的输电线路供电中断，约65万户居民受到影响，最长停电时间为31 h。文献［2-4］介绍了日本旭电机技术研究中心于1994年在易覆冰的山形县立川市专门设立导线覆冰试验线路，对耐雪环、偏心锤、相间间隔棒和线夹回转式分裂导线阻尼间隔棒等装置的舞动防御效果进行试验，试验结果表明线夹回转式分裂导线阻尼间隔棒具有较好的覆冰舞动防御效果。

针对超高压输电线路分裂导线截面大、架线高、档距长等易舞动的特点［5-6］，国内厂家也研制了线夹回转式导线阻尼间隔棒。目前，线夹回转式间隔棒已在安徽、山东、河南等十几个省市的输电线路上大量应用。但由于线夹回转式间隔棒的工程应用时间较短，还缺乏科学、有效的工程试验和理论评价检验，线夹回转式间隔棒的防舞效果和评价方法，安装位置优化及应用效益等都需要研究。本文根据输电导线和间隔棒的物理参数，研究防舞效果评价的理论与方法。

输电线路导线的舞动机理已有一定的研究成果［7］。其中，Den Hartog 和 O Nigol理论认为，导线的不均匀覆冰是舞动的重要因素，在同样地理和气候条件下，分裂导线比单导线更容易舞动［7-8］。线夹回转式间隔棒的特点是部分线夹可自由旋转，部分线夹固定不动，固定线夹依附在间隔棒本体上，回转线夹开有夹持导线的固定夹持孔，以夹持孔夹持中心线为中心连接在固定线夹上，使夹持的导线在其中能自由振动和扭转，扭转幅度范围为－90°～+90°，固定线夹的情况则相反。

由于电网规模越来越大，采用线夹回转式间隔棒改造线路的费用很大，线夹回转式导线阻尼间隔棒的防舞效果成了关注的热点。研究分裂导线的参数、舞动特性，认识线夹回转式导线阻尼间隔棒的防舞机理，提出间隔棒抑制舞动的评价方法是效果、效益评价的基础。

1 线夹回转间隔棒防舞机理

1.1 防舞机理

单导线与分裂导线覆冰的差异很大。输电线路的自身轴线一般是偏心覆冰而面向迎风侧的，导线覆冰后质量不平衡将会绕自身轴线扭转，覆冰导线在不断扭转、不断覆冰的过程中横截面形状变得均匀，起到了抑制导线舞动的效果。分裂导线每隔一段距离就有间隔棒将子导线固定起来，使子导线在间隔棒附近无法实现相应的转动。同时由于固定式的连接，增大了长度更短的次档距导线的扭转刚度。次档距的子导线需要更大的静扭矩才能扭转，导线很难产生绕自身轴线的转动。分裂导线的扭转系数比单导线大很多［9］，不均匀覆冰情况更为严重，因此分裂导线比单导线更易舞动。四分裂导线间隔棒和六分裂导线间隔棒实物如图1所示。

图1 线夹回转式分裂导线阻尼间隔棒Fig.1 Rotary clamp spacer-damper of bundled conductor

线夹回转式间隔棒的舞动防御原理如图2所示，可旋转线夹是防御舞动的关键所在。用间隔棒固定子导线时，使一半数量的子导线能在一定范围内转动，即便是在发生覆冰的情况下导线也能利用覆冰、积雪偏心质量扭转，通过绕自身轴线扭转而形成均匀的圆形覆冰。从而达到抑制导线覆冰舞动的目的。

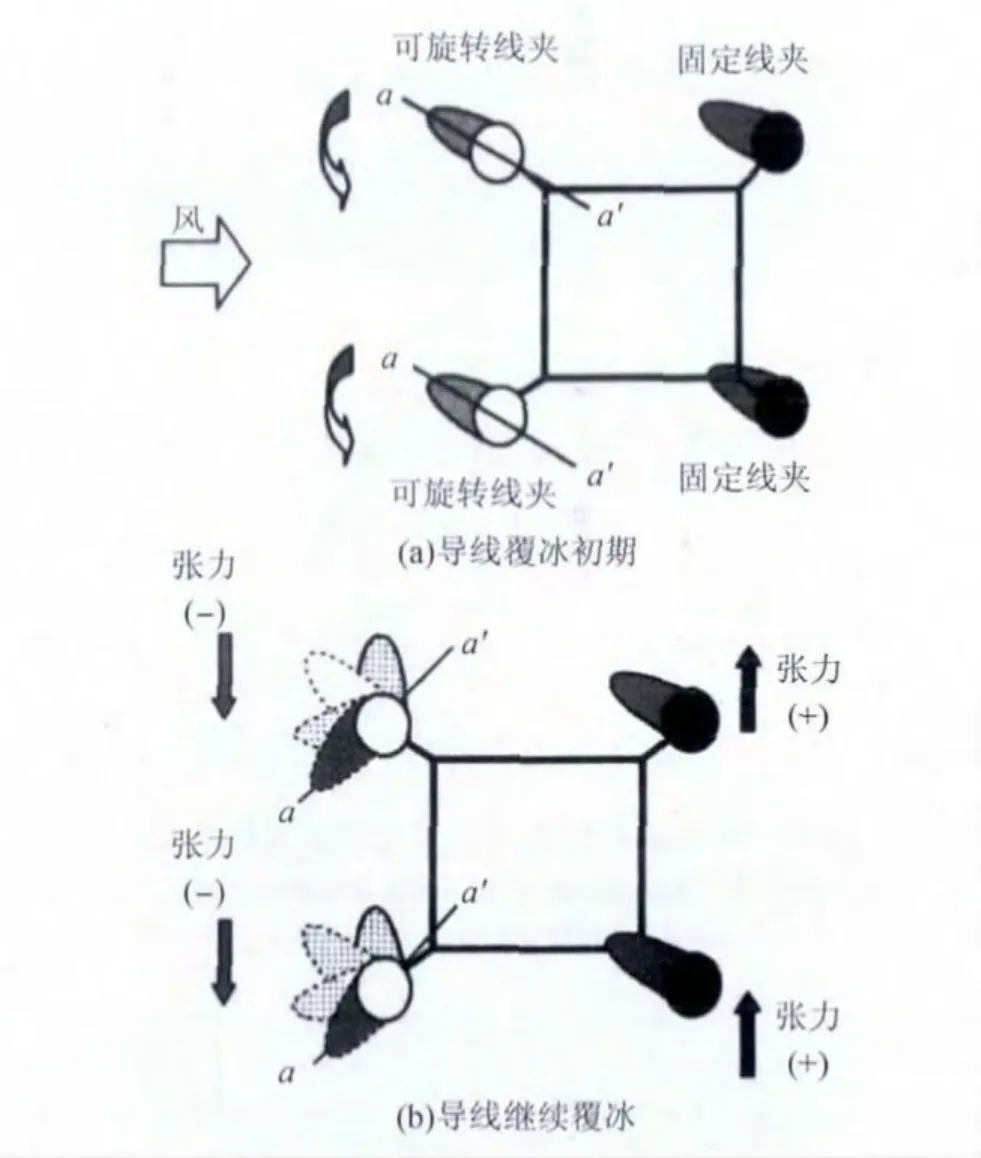
图2 线夹回转式导线阻尼间隔棒的舞动防御原理Fig.2 Anti-galloping principle of rotary clamp conductor spacer-damper

1.2 机理验证

为了验证上述防舞机理，即回转线夹对导线自身扭转的释放作用，可对导线偏心覆冰后自身的扭转性质进行研究。先假设初始覆冰角为0°，线路覆冰密度为900 kg/m3，导线参数及间隔棒分布见表1和表2［10］。然后通过改变初始覆冰厚度，比较偏心覆冰作用下回转线夹和固定线夹子导线的自身扭转情况。

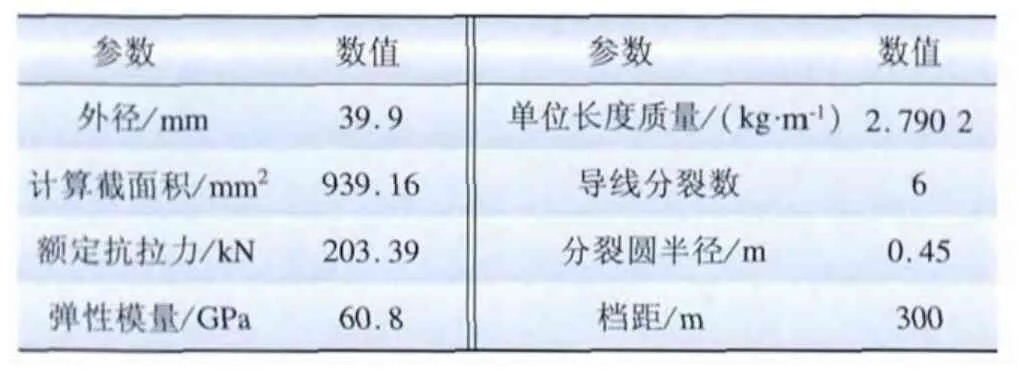
表1 导线计算模型参数Tab.1 Computational model parameters of conductor

表2 导线间隔棒布置情况Tab.2 Arrangement of conductor spacers

在同一分裂导线上，分别取1根由固定线夹夹持的子导线和1根由可回转线夹夹持的子导线，加载相同的覆冰扭矩作用，然后计算2根子导线绕自身轴线的扭转变化情况。图3为在初始覆冰厚度为10 mm的情况下，沿档长的2根子导线的扭转角分布情况。随偏心覆冰厚度(5～25 mm)的增加，2根子导线在档距中点附近扭转角的变化如图4所示。

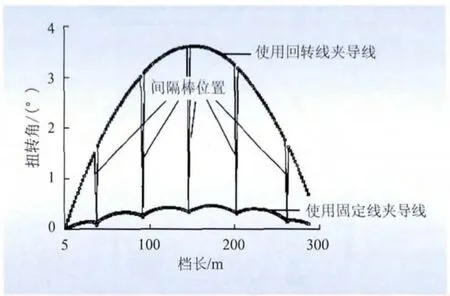
图3 10 mm初始覆冰厚度子导线扭转情况Fig.3 Twisting of sub-conductor when initial ice thickness is 10 mm

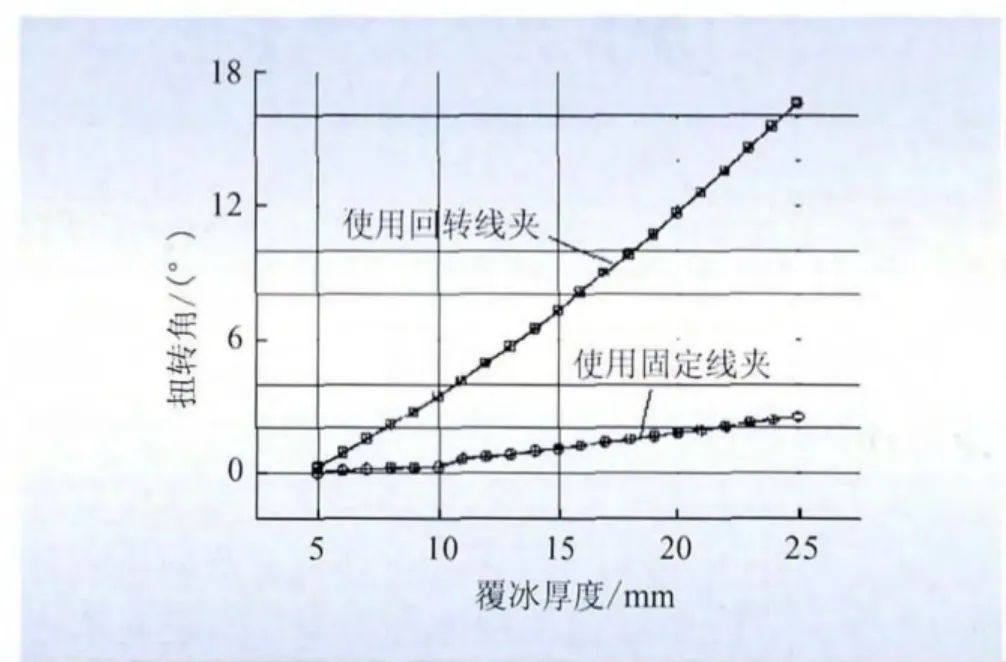
图4 子导线覆冰厚度与扭转角关系曲线Fig.4 Relation curves of conductor icing thickness and torsion angle

由图3、图4可以看出，导线覆冰扭矩随着冰层厚度的增加而增大，由档中的位置可知，子导线在固定线夹作用下的扭转角的变化率小于使用可旋转线夹导线的变化率。扭矩的增大对使用回转线夹的导线影响大，对使用固定线夹的导线影响小，即使用回转线夹的导线容易形成均匀覆冰，减小舞动的可能性。

2 导线间隔棒体系三维模型

2.1 导线模型

输电导线是细而长的柔性体，不能受压但可以受拉。分裂导线实际上是由间隔棒与多子导线组成的索梁［11］，采用有限元讨论舞动问题时，可将其作为连续振动系统、单自由度系统或多自由度系统处理。研究舞动振型时多使用连续系统。本文利用ANSYS Workbench软件分析四分裂导线的舞动振型问题，因此采用图5所示的四分裂导线三维连续系统模型，导线三维模型的建立基于如下假设［11］:

(1)输电杆塔及间隔棒呈刚性;

(2)输电导线的垂跨比数值很小;

(3)沿跨度方向的线路阻尼不予考虑;

(4)将导线和相邻杆塔简化为沿轴线方向的弹簧。

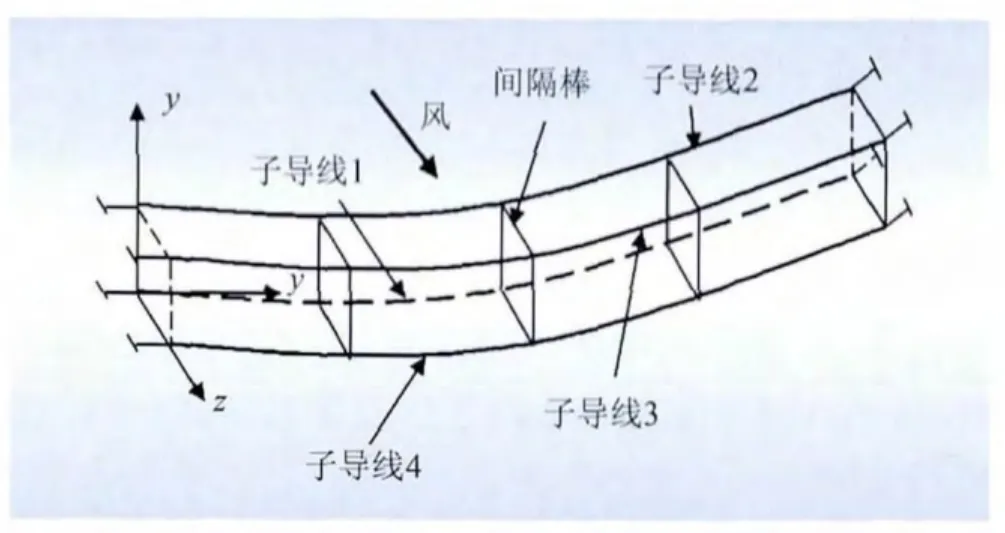
图5 四分裂导线模型Fig.5 Model of four-bundled conductors

2.2 导线阻尼间隔棒体系有限元模型

基于上述假设，在建模软件CATIA中，可建立间隔棒模型和导线阻尼间隔棒体系模型。本文仿真采用的导线型号为LGJ—240/30，导线参数见表3。将CATIA建立的导线阻尼间隔棒体系模型导入ANSYS Workbench有限元软件，可以得到导线阻尼间隔棒体系有限元模型。

考虑导线同时受轴向拉力、横向升力和阻力的影响，取2 m划分网格，在导线中点与轴线相垂直平面取80 cm×120 cm的计算区域，并在该区域导线表面做局部加密以增加计算的精度。由于输电线路呈细长结构，采用极坐标非结构划分网格和在导线边界区域对网格进行加密，网格总数约为18万个。

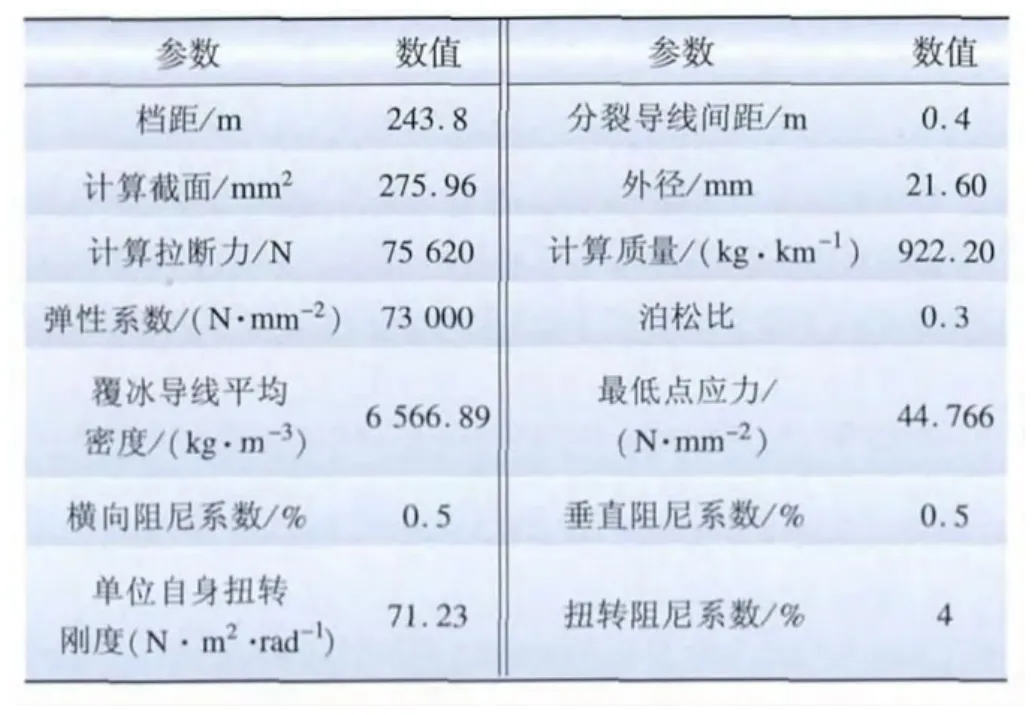
表3 导线的物理参数Tab.3 Physical parameters of conductor

3 导线阻尼间隔棒体系模态分析

3.1 模态分析过程

通过对有限元模型的模态分析，认识覆冰导线的动力特性，得到模态振型和固有频率，根据固有频率和振型给出舞动起决定作用的模态阶数，分析结果可为后续数值模拟仿真以及导线间隔棒的防舞布置提供理论依据。模态分析的求解过程如图6所示。

图6 模态分析步骤Fig.6 Procedure of modal analysis

3.2 模态仿真结果

导线模态决定导线的结构特性与材料特性，与外载荷无关。根据实际情况，设定的边界约束条件为:档距端点处节点的6个自由度约束。ANSYS仿真选用Subspace法的广义Jacobi迭代算法。通过仿真计算，可得到导线阻尼间隔棒体系模型前6阶模态的固有频率和固有频率振型图。固有频率见表4，其中6阶固有频率的振型图如图7所示。

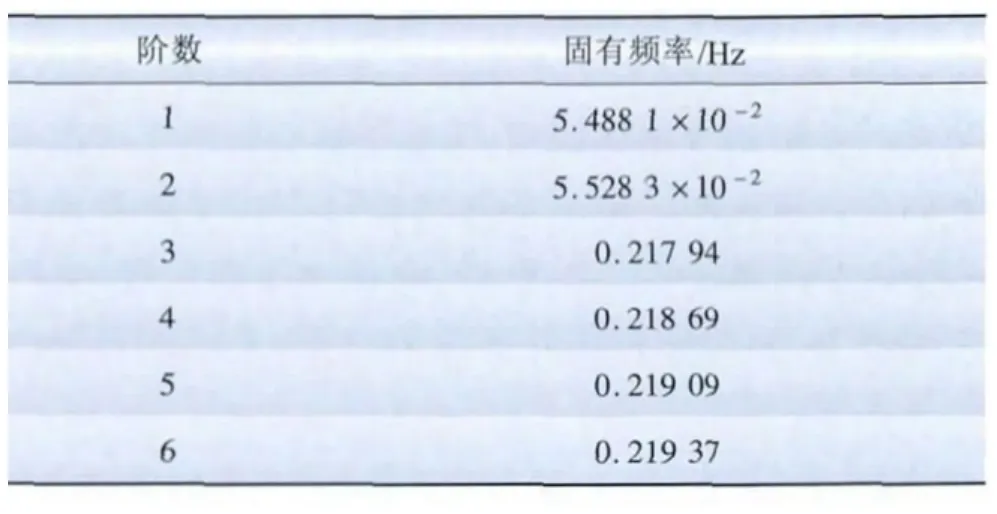
表4 前6阶模态固有频率Tab.4 Natural frequencies of the first six modal orders

图7 6阶固有频率振型图Fig.7 Vibration mode graph of the sixth order natural frequency

通过固有频率和振型图仿真计算可得到表5的分析结果。从表5可看出，导线的第1阶和第3阶、第5阶振型主要在xz平面内摆动，即顺风向舞动，分别为1个半波和2个半波;第2阶和第4阶、第6阶阵型主要在yz平面内摆动，即横风向舞动，分别为1个半波和2个半波。

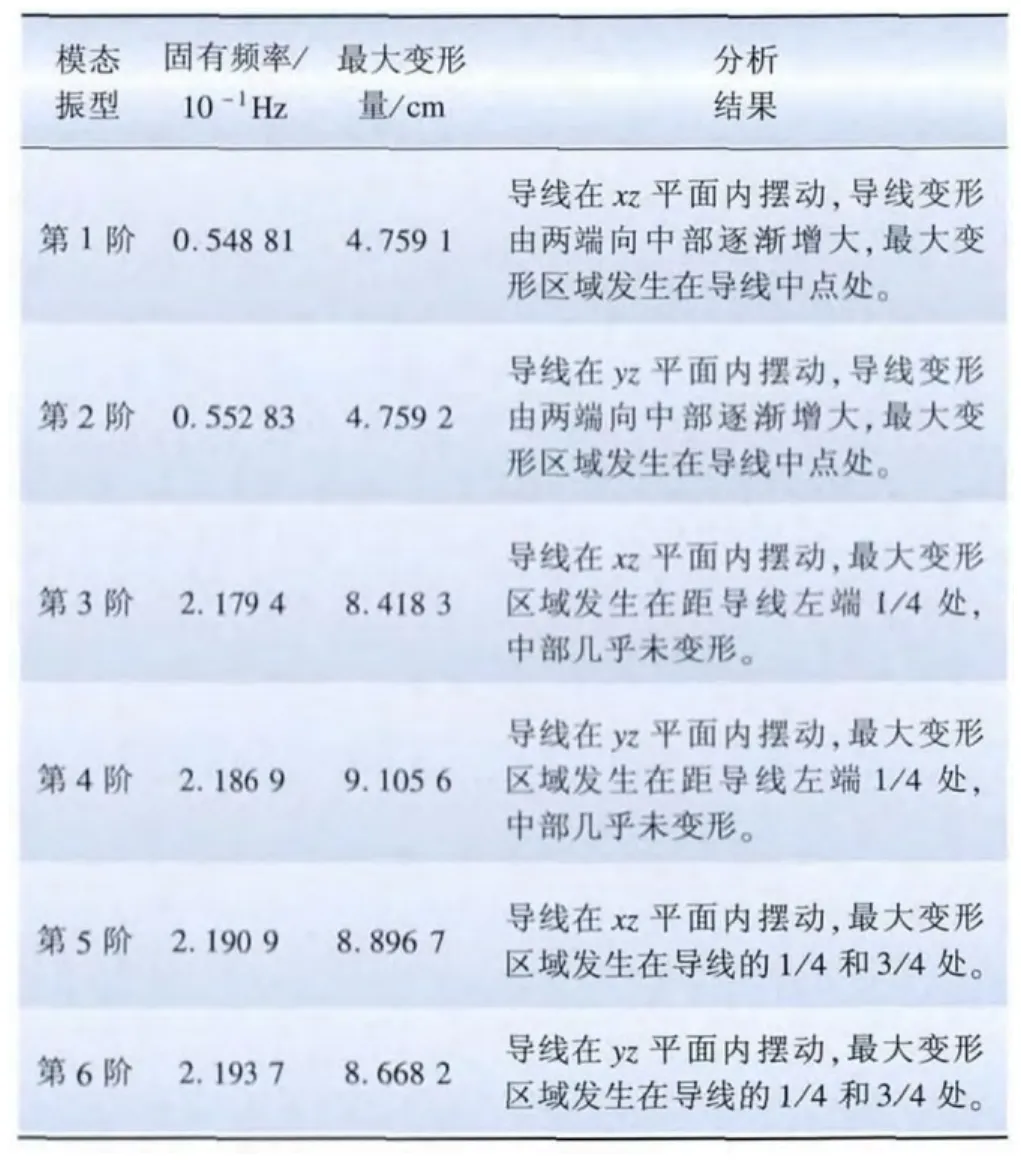
表5 振型分析结果Tab.5 Analysis results of vibration mode

前4阶振型与理论分析相吻合，第5阶、第6阶振型理论上应为3个半波，但受导线中部间隔棒的约束，而实际振型仅为2个半波。考虑到由于ANSYS仿真结果中缺少扭转振型，因此上述分析结果可以验证如今普遍认同的输电导线舞动形态以半波舞动为主要振型的结论［12-13］。此外，在振型波腹位置，导线振幅较大，应考虑在此处加装防舞器，能起到更好的防舞效果。

4 结论

(1)本文防舞原理分析和机理验证结果表明，可旋转线夹能部分地或全部地取消档距内线夹对子导线的扭转约束，从而使得导线覆冰的不均匀程度得到消除或减轻，达到一定的防御舞动的目的。

(2)分裂导线是由间隔棒与多根子导线组成的索梁，系统结构、材料特性和动力学特性极其复杂。使用ANSYS对导线间隔棒体系三维建模及模态分析结果表明，本文采用的Subspace法是求解导线间隔棒体系结构特性、动力学特性的有效方法，广义Jacobi迭代算法的模态仿真精度高，能反映导线的扭转、变形等情况。

(3)导线阻尼间隔棒体系6阶模态的固有频率和振型分析结果表明，本文分裂导线阻尼间隔棒体系的6阶振型的仿真分析结果与理论分析结果基本吻合，所采用的分析方法可以用于优化间隔棒以及其他防舞器的安装位置。了解导线阻尼间隔棒体系对不同类型动力荷载的响应，确定求解控制参数，认识导线阻尼间隔棒体系的固有振动频率和振型，有利于提高防舞效果。

［1］小田島.達彦新潟下越雪害の概要［J］.AEW 技報第36号，2007(12):2-5.

［2］三塚洋明，宍戸亮一，武田浩三，等.ルズスペサのギャロッピング抑制効果［J］.AEW 技報第30号，2001(12):7-10.

［3］今後の雪害対策のあり方について［C］//原子力安全·保安部会電力安全小委員会，2007.

［4］中野純.ギャロッピング現象と対策用ルズスペサについて［J］.AEW 技報第33号，2004(12):18-23.

［5］金成生.线夹回转式防舞间隔棒在特高压输电线路中的应用研究［J］.上海电力，2010(3):205-209.

［6］朱宽军，刘彬，刘超群，等.特高压输电线路防舞动研究［J］.中国电机工程学报，2008，28(34):12-20.

［7］郭应龙，李国兴，尤传永.输电线路舞动［M］.北京:中国电力出版社，2003.

［8］Yamaoka M，Hasegawa J.Fundamental characteristics of overhead transmission line galloping determined by simulating calculation using equivalent single-conductor method［J］.Electrical Engineering in Japan，1995，115(7):11-28.

［9］朱宽军，刘彬.架空输电线路分裂导线扭转刚度的计算［J］.电网技术，2010，34(3):10-18.

［10］朱宽军，刘彬，刘超群，等.特高压输电线路防舞动研究［J］.中国电机工程学报，2008，28(34):12-20.

［11］陈晓明.大跨越输电线舞动及其控制研究［D］.上海:同济大学，2002.

［12］王少华.输电线路覆冰导线舞动及其对塔线体系力学特性影响的研究［D］.重庆:重庆大学，2008.

［13］孙珍茂.输电线路舞动分析及防舞技术研究［D］.杭州:浙江大学，2010.