燃煤电厂锅炉燃烧系统的回声状态网络建模

孙灵芳，麻世博，赵瑞，赵光军

(1.东北电力大学自动化工程学院，吉林省吉林市132012;2.广州华润热电有限人司，广州市511455)

0 引言

燃煤发电厂的锅炉燃烧控制系统是一个“三入三出”的强耦合、非线性、大惯性、大延迟、参数时变和不确定的系统［1］，很难建立精确的、适应性强的模型，严重制约了锅炉燃烧系统优化和控制的研究。燃烧系统的模型辨识早期采用传统的方法，如理论建模法、阶跃响应曲线拟合法、子空间辨识法等［2-4］。这些方法较为简单，只能得到锅炉燃烧系统对象近似的传递函数或状态空间线性模型，模型精度较低。近年来，多使用智能算法建模，如利用支持向量机或T-S模糊模型建模，可以得到燃烧系统非线性模型，但无法适应燃烧系统的时变性和大延迟［5-6］。神经网络是近年来应用最多的燃烧系统辨识工具。锅炉燃烧系统建模多使用BP网络、RBF网络、小波网络等前馈神经网络，以及Elman网络等递归神经网络［7-10］。这些神经网络模型能够较精确地辨识燃烧系统的强耦合性和非线性，并可以采用动态训练算法提高对燃烧系统的时变性和不确定性的适应能力。

递归神经网络内部拥有延迟和反馈环节，可以准确地描述任意的非线性动态系统，具有很强的动态逼近能力，也能够适应辨识系统的大惯性和大迟延。回声状态网络(echo state network，ESN)是一种新型递归神经网络，其训练方法简单高效，训练时间和辨识精度在递归神经网络中也是最优的［11］。因此，本文选择使用ESN建立锅炉燃烧系统的模型。

本文将回声状态网络的结构进行了改进，并使用经过处理和优选的现场数据，采用改进的回声状态网络建立了锅炉燃烧系统的静态模型和动态模型，研究了燃烧系统的各种神经网络模型的精度和适应性。

1 回声状态网络简介

1.1 回声状态网络基本模型

ESN是一种新型的递归神经网络，是由Jaeger［12］于2001年提出的。图1给出了最常用的ESN的基本结构，由输入层、中间状态储备池(dynamic reservoir，DR)、输出层3个部分组成。DR包含了大量随机生成且稀疏连接的神经元，使得网络具有良好的短期记忆能力和非线性动态特性［11］。

图1 ESN的基本结构Fig.1 Basic structure of ESN

常用的ESN的状态方程为

输出方程为

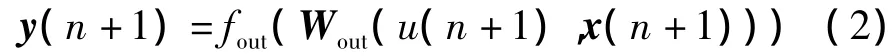
ESN训练时W、Win、Wfb按要求随机产生并不再变化。为使DR具有回声状态特性，W是稀疏矩阵，其连接密度φ为0.01～0.05，谱半径γ的绝对值小于1。训练时只需调整Wout的值，使得ESN训练变得更加简单、快捷。Wout的产生使用了线性回归的方法，只需要1次迭代就可以计算出Wout。

1.2 改进的回声状态网络

由于ESN的建模精度不理想，可以将ESN模型的结构进行改进，构造一种改进的回声状态网络(improved echo state network，IESN)用于锅炉燃烧系统的建模。由于ESN的W、Win、Wfb按要求随机产生，以及网络内部的反馈连接，网络输出有可能呈现不稳定的特性，训练输出会以一定的概率出现很大的误差。为减少训练输出不稳定的概率，可以在训练时对状态方程添加一定幅度的白噪声Av(n)［13］。v(n)为最大值为1的白噪声向量，其权值A一般较小。

为了改变各输入变量对状态储备池的贡献率，适应各变量之间的耦合程度，需要在输入变量u前乘以输入权值矩阵Gin。为了改变各输出变量对状态储备池的贡献率，适应各输入输出变量间的惯性和迟延，需要在输出变量y前乘以输出权值矩阵Gout。为了减少反馈到DR的输入，以保持网络输出的稳定性，在反馈进入状态储备池的输出反馈矩阵Wfb前乘以一个反馈权值矩阵Gfb。

综上，IESN的状态方程为:

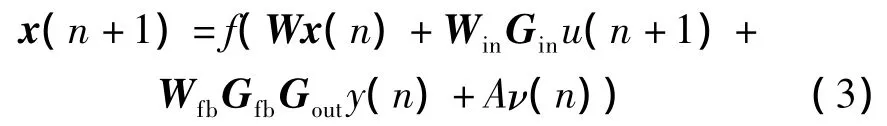
输出方程为:

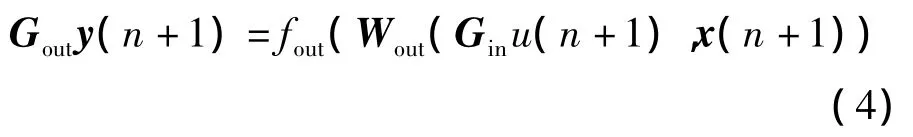
IESN的训练方法与ESN相同。

2 数据处理和数据优选

本文建模所需要的数据来自华电集团某燃煤电厂的一台300 MW机组，共采集了与锅炉燃烧系统有关的12个变量的数据，采样时间为1 s，采样点数为16 072点。首先，进行数据处理。使用邻域为49的3σ准则，将含有粗大误差数据用临近点的线性插值代替。采用7点邻域平滑滤波处理数据，去除数据中的部分噪声，并且将数据线性归一化至区间［－1，1］［14］。建模完成后，则需要按照前面归一化的参数，将训练输出数据反归一化，恢复数据的单位和数值。

然后，进行数据优选。在采集数据中的所有变量中，除3个主要输入变量和3个输出变量外，剩余的6个输入变量，作为干扰，都会对3个输出量在理论上产生一定的影响，需要从中选出几个辅助输入变量与主要输入变量一同作为神经网络的输入。本文采用平均影响值(mean impact value，MIV)算法［15］，根据9 个输入变量MIV的相对大小，同时考虑理论上各输入变量与输出变量的关系，选取了3个变量为锅炉燃烧系统建模的辅助输入变量。模型的输入输出变量如图2所示。

作为神经网络的输入数据，需满足致密性、遍历性、相容性等要求［16］，才能使用数据建立足够精确的神经网络，使神经网络的预测误差足够小。综合上述3点要求，本文选取处理后的现场数据中的第12 101至13 100共1 000组输入输出数据作为导师数据，用于网络训练，选取第13 301至13 400共100组输入输出数据，作为标准预测数据用于预测。

图2 神经网络模型的输入输出变量Fig.2 Input and output variables of Neural Network

3 锅炉燃烧系统的静态建模

3.1 ESN与IESN的比较

为了比较ESN和IESN的建模性能，用2种网络分别建立锅炉燃烧系统的静态模型，并将模型的性能进行比较。模型性能中，建模精度，用网络的训练误差，即网络训练输出数据相对于导师输出数据的平均绝对误差(mean absolute error，MAE)来量度［17］;适应性，则用网络的预测误差，即预测输出数据相对于标准预测输出数据的MAE表示;建模效率，则用建模用时，即模型训练和预测程序的运行耗时来评价。ESN中，其DR神经元个数N、连接密度φ、谱半径γ、导师信号的起始时间点T0这4个参数，及IESN中上述4个参数及噪声权值A、输入权值矩阵Gin、输出权值矩阵Gout和反馈权值矩阵Gfb共8个参数，对网络的训练和预测误差大小都有重要的影响。本文采纳上述参数的经验取值范围，并结合锅炉燃烧系统的实际情况进行尝试，测试得到了ESN和IESN的上述参数的最优值。

2种静态模型的性能如表1所示。采用最优参数ESN和IESN的锅炉燃烧系统静态模型输出数据的绝对误差如图3所示。ESN结构改进后，模型的建模用时基本不变，训练误差和预测误差都有明显的降低，模型的精度和适应性都有所提高。因此，本文选用IESN建立锅炉燃烧系统的静态模型。

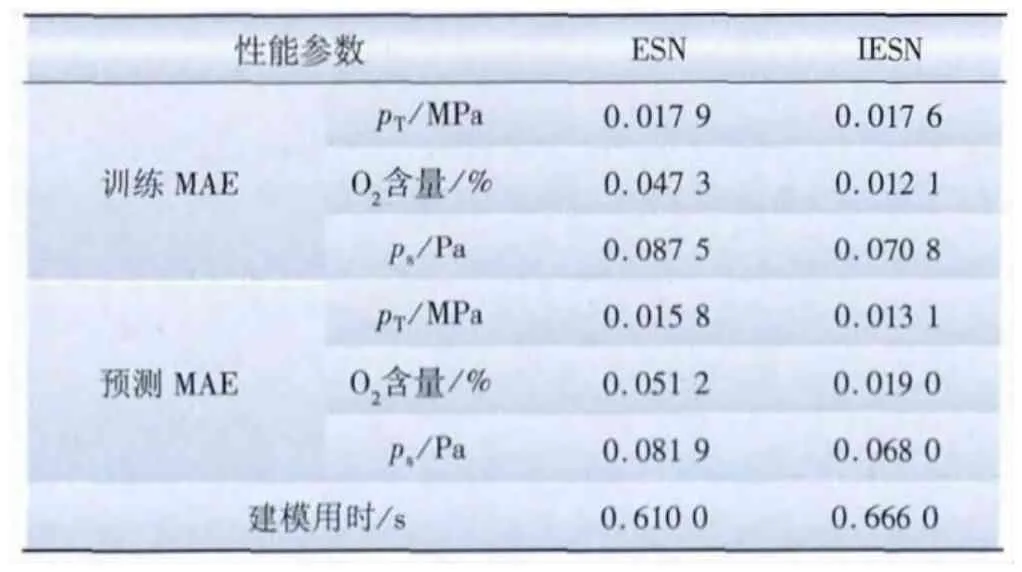
表1 ESN与IESN静态模型的性能Tab.1 Performances of ESN and IESN static models

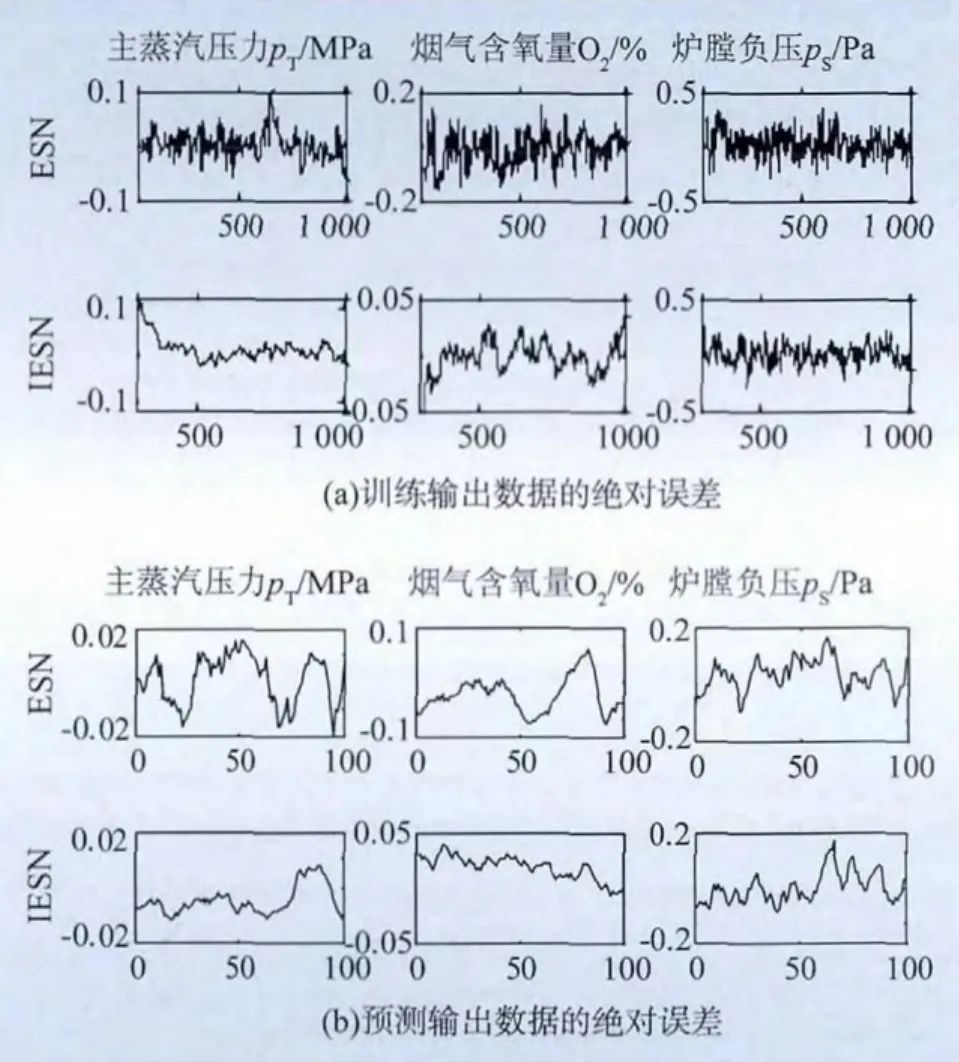
图3 ESN与IESN静态模型输出数据绝对误差Fig.3 Absolute error of ESN and IESN static model output data

3.2 IESN与其他神经网络的比较

本节将使用IESN建立的锅炉燃烧系统的静态模型，与3种前向型神经网络:BP网络、RBF网络、广义回归神经网络(general regression neural Network，GRNN)，及1种递归神经网络:Elman网络分别建立的锅炉燃烧系统的静态模型的性能进行比较，以验证IESN的优势。

5种神经网络静态模型的性能如表2。5种神经网络静态模型的输出数据的绝对误差如图4所示。在这5种神经网络构建的锅炉燃烧系统静态模型中，IESN模型的精度较高，训练误差较低，适应性最强，预测误差明显低于其他网络，而且建模用时较短，是性能最优的锅炉燃烧系统静态模型。

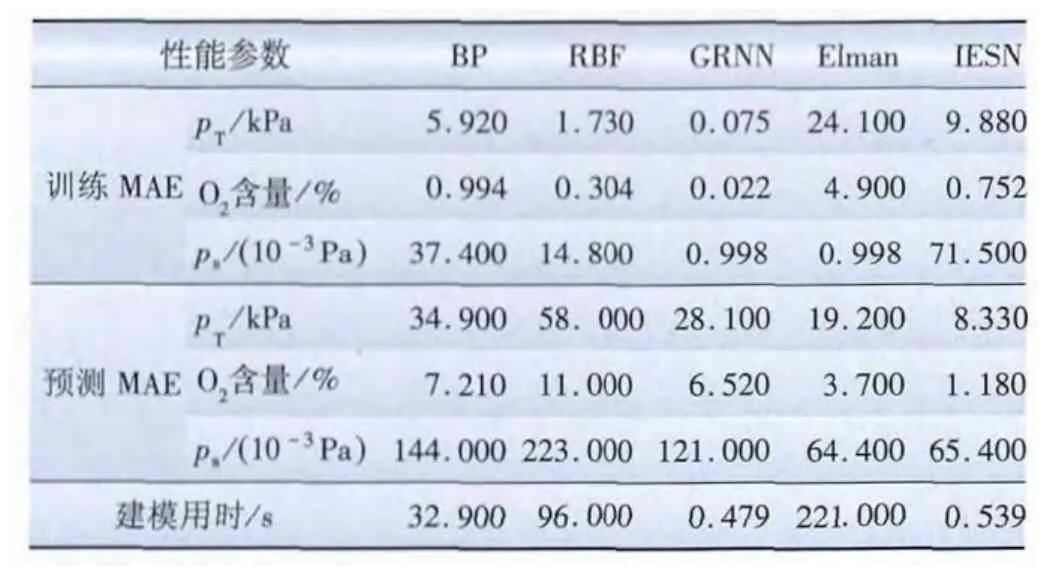
表2 5种神经网络静态模型的性能Tab.2 Performances of five types of Neural Network static models

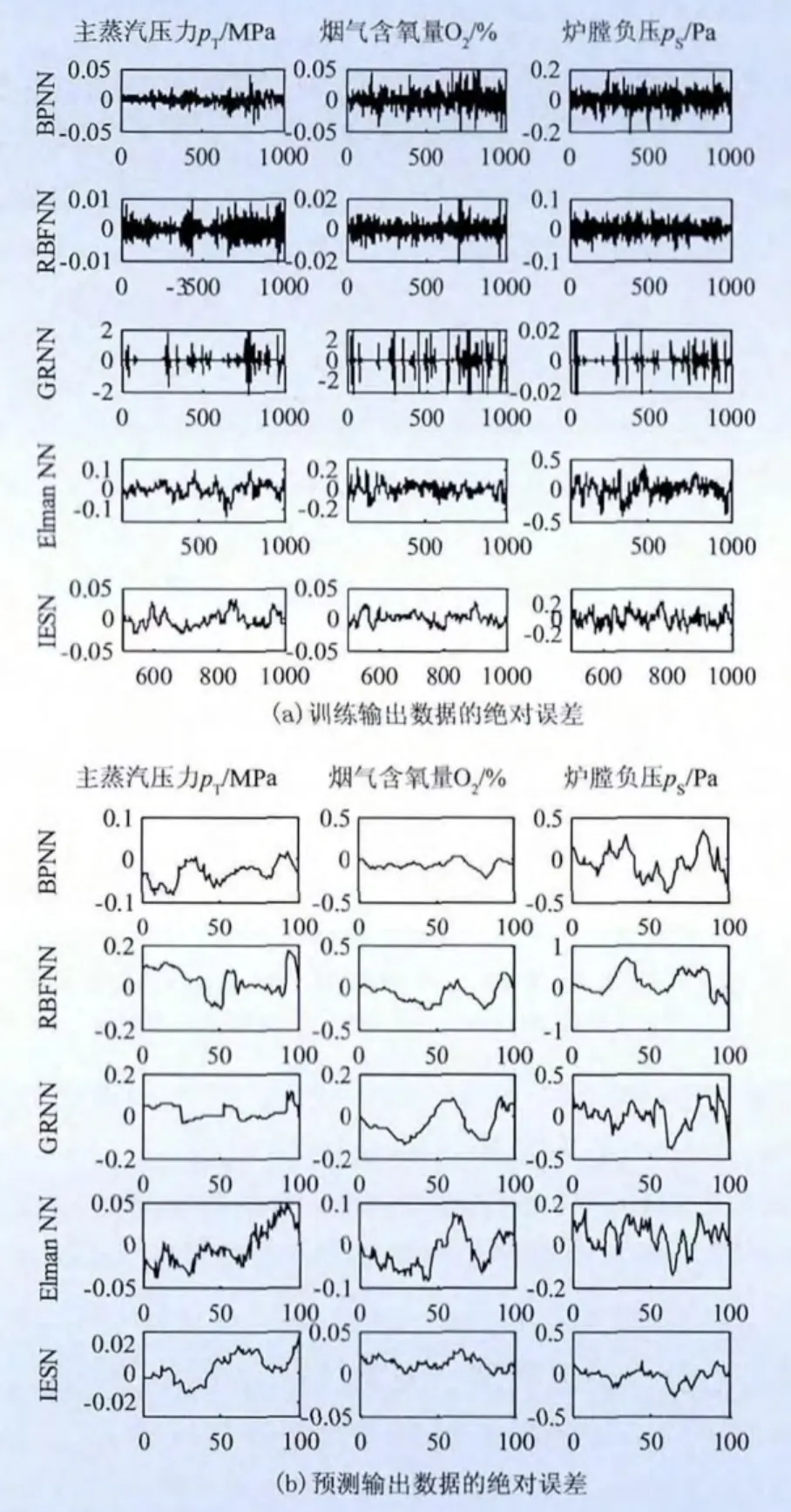
图4 5种神经网络静态模型的输出数据的绝对误差Fig.4 Absolute error of five types of Neural Network static model output data

4 锅炉燃烧系统的动态建模

ESN网络的训练采用线性回归的方法，一次迭代就能直接计算出最优的网络权值，节省了大量的时间。因此，可以采用单步迭代动态预测的方式，先选择一个训练误差较低的网络作为初始网络，每一步都更新训练数据，重新训练初始网络，每一步只预测1个输出。这种动态ESN模型由于使用历史数据动态更新网络，能够更好地适应锅炉燃烧系统的时变性和不确定性，在预测时间较长，燃烧系统的模型参数随负荷大范围变化时能够显著降低预测误差。

由于静态模型和动态模型采用同样的训练数据和训练算法，两者的训练误差是相同的，只需对比预测效果。预测持续时间为500 s时，静态模型、动态模型的预测输出数据的绝对误差如图5所示;2种模型的预测误差与预测用时如表3所示。动态模型与静态模型相比，预测误差降低了80%左右;动态模型虽然耗时较长，但平均每一步预测的耗时为0.264 s，在可接受范围内。观察二者的绝对误差曲线可知，预测时间较长时，动态模型的预测误差保持稳定，而静态建模的预测误差逐渐增加。因此动态模型适应性更好，更适合长时间预测。

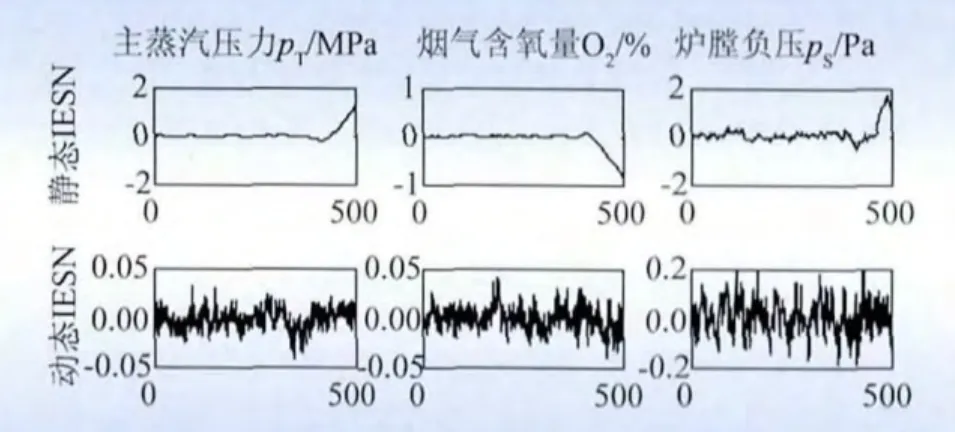
图5 静态模型与动态模型预测输出数据的绝对误差Fig.5 Absolute error of static model and dynamic model prediction output data

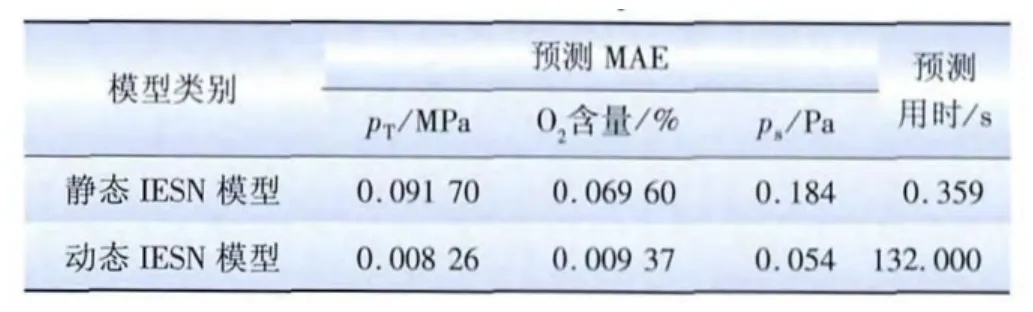
表3 静态模型与动态模型的预测误差和预测用时Tab.3 Prediction error and prediction consuming time of static model and dynamic model

5 结语

本文首先将回声状态网络的结构进行了改进，提高了网络的精度和适应性。使用经过处理和优选的现场数据，建立了锅炉燃烧系统的改进回声状态网络静态模型，与其他神经网络模型相比，精度较高，适应性最好。本文又采用改进的回声状态神经网络建立了锅炉燃烧系统的动态模型，其与静态模型相比，适应性更好，更适合于长时间的预测。

［1］刘禾，白焰，李新利.火电厂热工自动控制技术及应用［M］.北京:中国电力出版社，2009:153-189.

［2］周荣，江青茵，曹志凯，等.440 t/h循环流化床锅炉整体动态模型及仿真［J］.厦门大学学报:自然科学版，2007，46(2):288-232.

［3］张伟伟.工业锅炉燃烧系统辨识与建模研究［D］.上海:上海交通大学，2007.

［4］刘芳，张德珍，赵文杰.电站锅炉燃烧系统的神经网络建模［J］.电力科学与工程，2010，26(6):33-37.

［5］费洪晓，黄勤径，戴弋，等.基于SVM与遗传算法的燃煤锅炉燃烧多目标优化系统［J］.计算机应用研究，2008，25(3):811-813.

［6］黎倩.模糊鲁棒控制在循环流化床锅炉控制中的用研究［D］.石家庄:河北科技大学，2010.

［7］马翔，陈新楚，王劭伯.基于RBF神经网络的电站锅炉燃烧系统非线性建模［J］.福州大学学报:自然科学版，2004，32(3):295-298.

［8］Li J，Liu J Z，Niu Y G.Application of Neural Network Model Reference Adaptive Control in Coal-Fired Boiler Combustion System［C］//Proceedings of the Third International Conference on Machine Learning and Cybemeucs，Shanghai，2004:564 －567.

［9］Hong W J，Jiang Q Y，Cao Z K.Wavelet-Network-Based Predictive Model in Combustion Process of CFBB［C］//14th International Conference on Mechatronics and Machine Vision in Practice，Xiamen，2007.

［10］卢勇，徐向东.基于神经网络模型的锅炉广义预测控制［J］.热能动力工程，2011，16(1):55 －60.

［11］章国升.基于递归神经网络的非线性系统辨识研究［D］.兰州:兰州大学，2010.

［12］Jaeger H.The Echo State Approach to Analysing and Training Recurrent Neural Networks［R］.GMD Report 148:German National Research Center for Information Technology，2001.

［13］Jaeger H，Haas H.Harnessingnonlinearity:predictingchaotic systems and saving energy in wireless telecommunication［J］.Science，2004，4:78-80.

［14］旷潇潇.基于时滞型神经网络覆冰预测可行性分析［J］.科技论坛，2012(1):98-99.

［15］王建星，付忠广，靳涛，等.基于广义回归神经网络的机组主蒸汽流量测定［J］.动力工程学报，2012，32(2):130-135.

［16］周斌，李玉梅，志贺圣一.神经网络内燃机排放模型学习样本的选定［J］.西南交通大学学报，2002，37(6):659-663.

［17］李启权，王昌全，张文江.基于神经网络模型和地统计学方法的土壤养分空间分布预测［J］.应用生态学报，2013，24(2):459-466.