基于支持向量机方法的输电工程造价指标评估体系

2014-02-13王绵斌李欢欢谭忠富张金良

电力建设 2014年3期

王绵斌，李欢欢，谭忠富，张金良

(1.国网冀北电力有限公司经济技术研究院，北京市100070;2.华北电力大学电力经济研究所，北京市102206)

0 引言

充足稳定的电力供应是维持我国经济快速发展的重要条件之一。然而随着各产业的加速发展、人民生活水平的日益提高，需要进行大量电网基础设施建设以满足不断增长的电力需求。“十二五”期间，国家电网公司将积极推进智能电网的建设，电网投资1.7万亿元。巨大的投资和繁重的建设任务将对工程造价管理提出更高的要求。建设管理单位需要加强对工程造价预测和造价控制的研究，把握输电工程造价规律，提升科学管理水平。因此，如何在初设阶段利用已建工程的造价信息，采用科学的方法对历史数据进行分析和预测，把握工程数据之间的内涵规律，准确、高效地对工程评审进行指导变得非常重要。

当前国内对于工程造价的研究，主要从模糊数学、灰色关联度和人工神经网络、支持向量机等方法入手。文献［1］根据概率论和模糊数学原理，确立随机模糊数学特征统计方法，应用贴近度理论估算出子工程费用，叠加子工程费用构成总体工程费用的近似造价值。文献［2-4］利用灰色系统理论估算了建筑费用，其中将预估工程项目和类似工程项目进行分解，以分部工程为计算起点，计算分部工程特征和造价关联度。文献［5-9］研究如何将神经网络与聚类技术、遗传算法等理论结合提高网络学习能力。文献［9］研究了支持向量机在电力输电工程造价估算方法中的应用。但模糊数学对于工程造价的复杂问题描述过于简单，估算结果粗糙;灰色关联理论过高估计了不同工程的造价相似度，准确度不高;神经网络方法则要求样本具有较大的规模。输电工程费用的构成和影响因素众多，以上方法难以在小样本的基础上建立符合精确度要求的造价评估指标体系。为提出一种易于操作、快速有效的电力工程造价小样本估算模型，需要结合工程造价历史数据的具体特点，从数据处理、数据降维、指标建立和测算各方面进行优化处理。

本文在传统输电工程造价指标体系的基础上，重新研究从样本统计到指标建立和验证整个指标体系建立流程中的新方法，选取影响因数简化处理［10-12］、基于主成分分析、粒子群优化的最小二乘支持向量机［13-14］等方法，建立输电工程造价三级指标体系。

1 基于粒子群优化的最小二乘支持向量机方法

对于一个给定的样本集(xi，yi)，i=1，2，…，l，xi∈Rn，yi∈R，用非线性映射 φ(·)把样本集从输入空间映射到特征空间，然后在高维特征空间中进行线性回归:

根据结构风险最小化原理，回归问题可以转化为

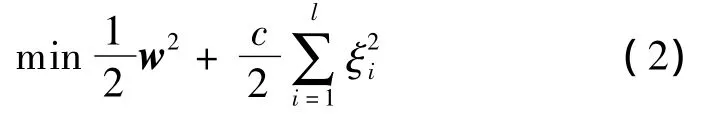
约束条件:

式中:w为最小二乘支持向量机(least squares support vector machine，LSSVM)的权值系数;b为常值偏差;c为惩罚因子;ξi为松弛因子。

为求解该约束的最优化问题，通过引入拉格朗日函数，由 KKT条件求解，最终可以得到如下的LSSVM回归函数模型:

LSSVM常用的核函数有径向基函数、多项式函数、线性函数等。研究表明径向基函数具有较强的泛化能力，因此本文选用径向基核函数，其表达式如下:

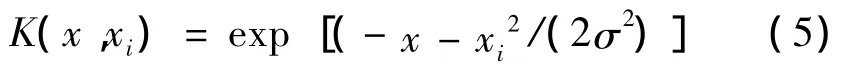
此时，LSSVM的参数选择问题即为核函数参数σ与惩罚因子c，参数［σ，c］将由粒子群优化算法给出。

粒子群优化算法是由Eberhart博士和Kennedy博士于1995年提出的一种进化计算方法，其基本思想是通过群体中个体之间的信息传递及信息共享来寻找最优解。设粒子群群体规模为M，每个粒子在D维空间飞行，初始速度为 vi=［vi1，vi2，…，vid］，初始位置为一随机变量 ui=［ui1，ui2，…，uid］，i=1，2，…，M，d=1，2，…，D，则每个粒子是通过2个“极值”来寻找最优解，一个是粒子本身的最优解pbesti，用Pi=［pi1，pi2，…，pid］表示;另一个是整个种群目前的最优解gbest，用 Pg=［pg1，pg2，…，pgd］表示。

根据粒子适应度值，即可得到如下的粒子更新的速度和位置，直到符合终止条件:

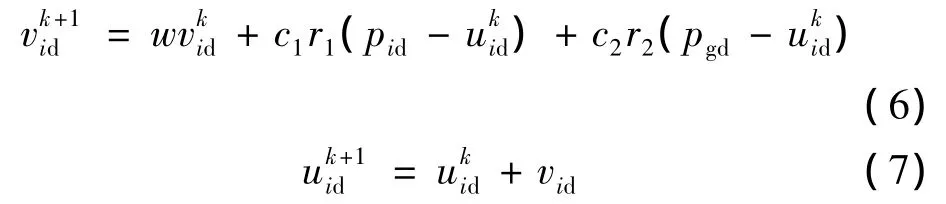
式中:k为迭代次数;c1，c2为加速因子，它们使得每个粒子分别向 pbesti和 gbest的位置靠近;r1，r2为［0，1］间随机数;w为惯性权重系数，是一个非负数，w取值较大时，全局搜索能力较强，反之局部搜索能力较强，在进化初期通常给w设置一个较大值以提高算法的全局搜索能力，随着迭代的进行而缩小。

2 输电工程造价指标评估体系

根据输电工程造价样本建立500 kV输电工程造价指标评估体系，建立的整体逻辑流程如图1所示。

2.1 工程样本处理与造价关键影响因素分析

本文共收集某电力公司系统内2008—2012年间竣工投产的500 kV输电概算工程原始数据样本47个，以输电工程造价构成特点和一般规律为依据，运用ABC法确定构成输电工程造价的主要费用，进一步挖掘影响输电工程造价的关键影响因素，分析各个关键影响因素对于工程造价的影响程度以及与工程造价的关系。

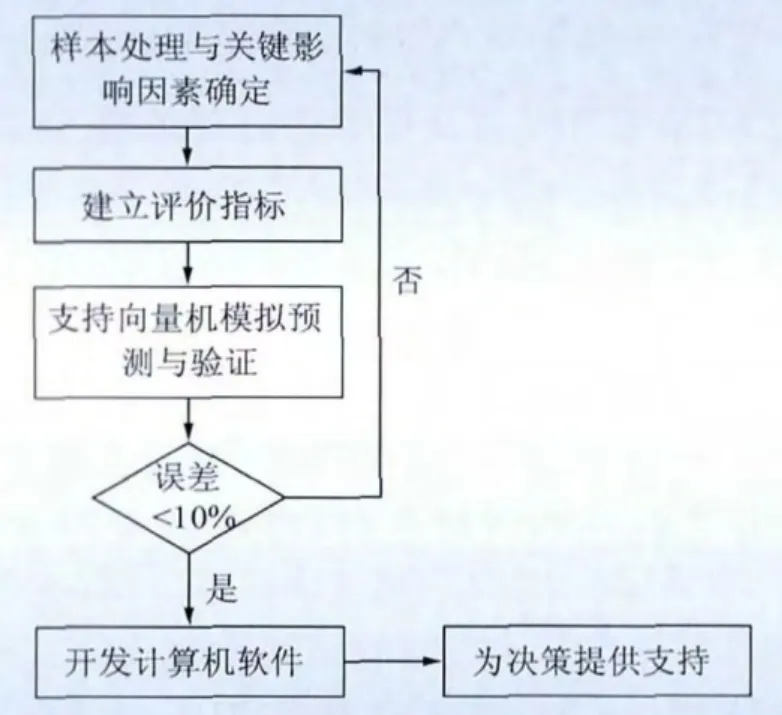
图1 输电工程造价评估指标体系建立流程Fig.1 Building process of transmission project cost evaluation index system

关键影响因素的确定过程中存在两大难点:(1)造价影响因素众多:既有系统因素，如输电容量;也有环境因素，如地形、地质等;还有设备因素，如导线、杆塔的类型及价格等。若计算参数选取过多，将增加造价分析的复杂性。(2)影响因素间存在一定的相关性:如塔材量、塔材价格、塔材造价存在推导关系，耐张塔基数、转角次数间存在相关关系等。若逐一进行分析会使影响程度重复叠加，不剔除影响因素间的相关性，势必会放大各影响因素对造价的影响。故首先需进行样本与关键因素的简化处理，其具体处理流程和操作见表1。

表1 数据处理流程与操作Tab.1 Processing flow and operation of data

结合处理后的样本实际情况，通过数据统计及专家评定确立出各类费用的关键影响因素，见表2。静态投资的关键影响因素为各个主要费用因素的关键影响因素的整合。

表2 输电工程各部分费用关键影响因素Tab.2 Key influencing factors of cost in each part of transmission project

2.2 建立三级评估指标体系

综合输电工程费用构成的特点，将输电工程静态投资作为一级指标，静态投资的各个主要费用因素作为二级指标，再根据二级指标的关键影响因素求解三级指标及其计算公式。

在求解三级指标的过程中，采用主成分分析法对关键影响因素进行降维。以二级指标的关键影响因素作为输入集，利用SPSS软件计算相关系数矩阵，判定得到各个关键影响因素之间具有较强的相关性，证明样本数据可用于主成分分析。在此基础上，得出各成分对于总方差解释程度的特征值表和主成分载荷矩阵(数据协方差矩阵的特征值矩阵)表。提取特征值大于1的前m个成分因子作为该费用项的主成分，以主成分载荷矩阵中的数据除以主成分相对应的特征值开平方根，得到主成分中每个指标所对应的系数［15-16］，即，其中 Cif为载荷矩阵中主成分i中因素f的值，λi为主成分i的特征值。

以关键影响因素较少的基础工程为例做简要说明，表3为实际34个样本数据，任取其中32个作为基础数据，2个样本留作检验样本。运用SPSS软件进行主成分分析得到表4～6，表4～6分别为解释的总方差表、主成分载荷矩阵表、指标系数表。

由表4、表5求解表6的方法为:表5中成分1对应列的数据，除以表4中成分1对应的“合计初始特征值”的正平方根，得到表6中成分1对应列的数据。将表6中成分1作为新的三级指标，将其对应列的数值作为三级指标由关键影响因素计算的公式系数，至此建立了基础工程的三级评估指标。

表3 基础工程样本数据Tab.3 Sample data of foundation engineering

2.3 支持向量机预测与验证

通过Matlab实现支持向量机算法，结合处理后的34个实际样本，以其中32个样本作为学习样本，其他2个样本作为测算样本进行预测与验证。以各费用项所对应的主成分载荷矩阵与学习样本中关键影响因素实际值进行矩阵相乘得到的数据作为预测依据，以2个测算样本的关键影响因素值作为输入集，得到各二级指标的预测数据，该数据与实际样本的对比见表7。

表4 基础工程解释的总方差Tab.4 Total variance explained of foundation engineering

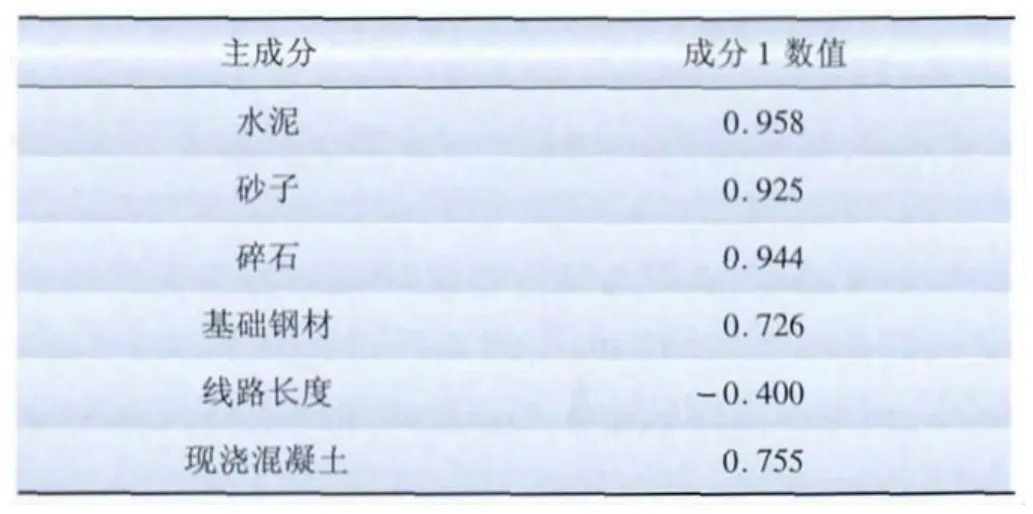
表5 基础工程主成分载荷矩阵Tab.5 Component load matrix of foundation engineering

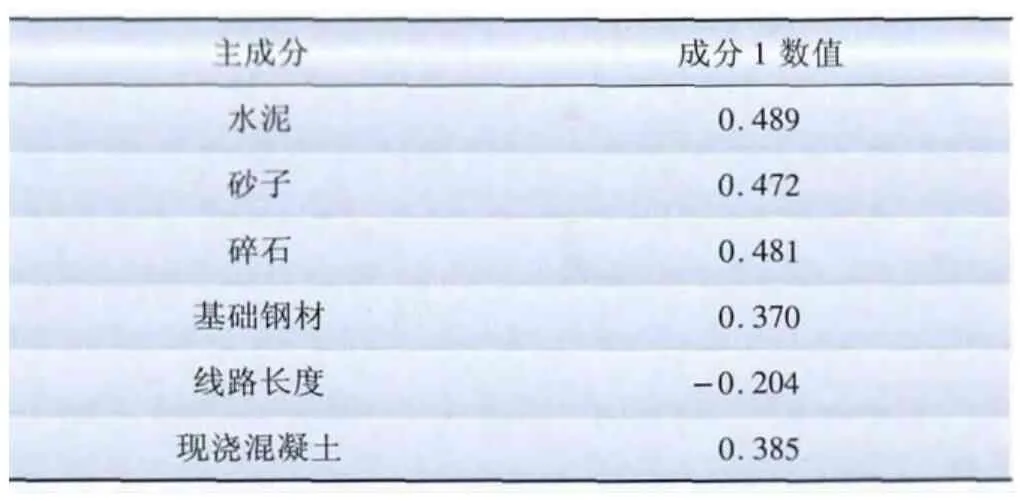
表6 基础工程指标系数矩阵Tab.6 Index coefficient matrix of foundation engineering

由表7可知各个预测的偏差值均能控制在10%的范围内，表明该评估指标具有较大的可靠性和实用性。同时本文进行了各项二级指标的安全区间确定。给定显著性水平α，使得对应于某特定的单点估算值落在区间(T1，T2)的概率为1－α，即指标的安全区间为，本文取 α =0.1。得到测试样本的500 kV输电工程概算阶段各部分费用安全区间见表8。

2.4 相关计算机软件开发

由预测和验证结果可知，利用本文所建立的三级输电工程造价评估指标与支持向量机方法进行输电工程造价预测的误差能够控制在10%以内，具有较高的预测准确度，在前文研究结果的基础上开发了基于支持向量机方法对输电工程造价进行预测的计算机软件，以期为实际输电工程造价决策提供有价值的参考信息。

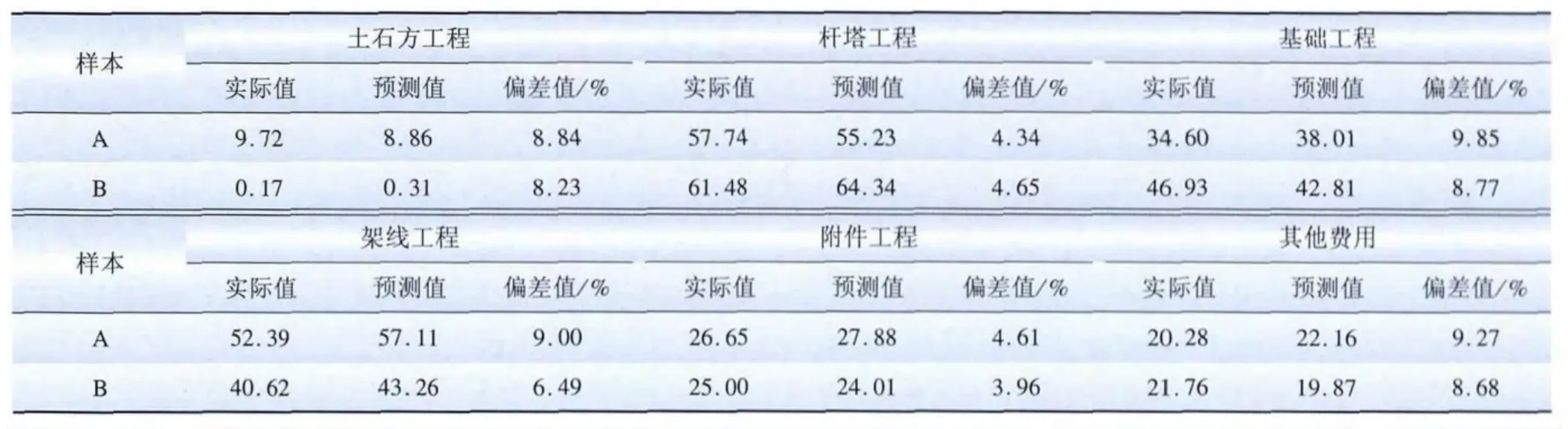
表7 预测结果与偏差对比Tab.7 Prediction results and deviation万元

表8 各部分费用安全区间Tab.8 Security zone of each part cost万元

3 结论

输电工程的费用构成与影响因素众多，且样本统计参差不齐，若对所有的影响因素进行统计和处理、预测，则会带来不必要的工作量或者频繁遇到数据缺失项、奇异点过多等问题，但若考虑的因素过少则不能很好地体现出工程造价的实际情况，造成预测值偏差大。为了建立实用、可靠的输电工程造价评估体系，本文先后采用ABC分析法、关键参数简化处理方法、主成分分析法对样本进行了处理，通过计算得到了三级指标及其计算公式，进一步利用基于粒子群优化的最小二乘支持向量机方法对该评估指标体系做出了测算与验证，证明了其具有较高的预测准确度，该方法可为500 kV输电工程造价管理提供有价值的参考信息。

［1］唐晓阳.工程项目投资费用的随机－模糊估算方法研究［J］.清华大学学报:自然科学版，1996，36(4):13-18.

［2］张协奎，钱永峰.基于灰色关联分析的建筑工程费用估算［J］.建筑经济，2000(6):41-42.

［3］张清梅，陈瑜.用聚类分析法估算建筑费用［J］.国外建材科技，2001，22(2):77-78.

［4］荀志远，于彩华.加权灰色关联度法在工程投资估算中的应用［J］.建筑技术开发，2001(9):26-29.

［5］邓焕彬，强茂山，刘可.基于神经网络的公路工程造价快速估算方法［J］.中南公路工程，2006，31(3):127-131.

［6］李驰宇.高速公路造价快速估算模型与方法的研究［D］.成都:西南交通大学，2006.

［7］王颖.数据挖掘技术在电力线路工程造价管理中的应用研究［D］.重庆:重庆大学，2008.

［8］王颖，俞集辉，王玉斌.基于软计算的电力线路工程造价预测模型［J］.计算机仿真，2008，25(8):246-250.

［9］熊燕.基于人工智能技术的建筑工程造价估算研究［D］.南昌:华东交通大学，2008.

［10］彭光金.小样本工程造价数据的智能学习方法及其在输变电工程中的应用研究［D］.重庆:重庆大学，2010.

［11］韦俊涛.电力工程造价小样本估算模型研究［D］.重庆:重庆大学，2009.

［12］司海涛.有小样本数据特征的输变电工程造价估算与灵敏度研究［D］.重庆:重庆大学，2010.