加权社交网络节点中心性计算模型

李静茹，喻 莉，赵 佳

(华中科技大学电子与信息工程系 武汉 430074)

确定网络中的关键节点是包括社交网络在内的复杂网络的重要研究内容。比如，在各种社交网络中，经常需要知道哪些是最活跃、最具影响力的用户，以便为运营商提供营销策略的指导，或为移动社交网络的内容分布提供有用依据。在社会网络分析中，用“中心性(centrality)”来刻画节点在网络中的重要程度[1]。

中心性常用的度量方法有度中心性、介数中心性、接近中心性[2]和特征向量中心性(EVC)[3]等。相比其他几种中心性度量方法，EVC不仅考虑了节点的度(即邻居节点的数量)，还考虑了邻居节点的重要性，因此成为检测社交网络中最具影响力节点的成功方法，并在社会科学中有广泛应用[4]。而由于EVC是将邻接矩阵对应的主特征向量作为节点中心性，故最重要的一些节点集中于一个社团；而事实情况往往是这些最具影响力的节点分属于不同社团。鉴于此，文献[4]提出了主分量中心性(PCC)，利用邻接矩阵的前P个特征向量来计算节点中心性，有效地避免了EVC的缺陷。文献[5]针对PageRank方法在非连通网络中排序不唯一的缺陷，提出了LeaderRank方法，网络中增加一个与所有节点双向连通的节点，使得整个网络连通且排序唯一，在传播效率、鲁棒性和容错性方面有明显的提升。文献[6]针对度中心性的低相关性和介数中心性、接近中心性在大型网络中的高复杂度，折中提出一种半局部中心性，在降低计算复杂度的同时能很好地识别出影响力高的节点。

而以上方法均针对无权网络，只考虑了节点间是否连接，而未考虑节点间链接强度如何。而文献[7]提出，很多网络中的链接并不仅仅表示存在与否，而是有相应的权重来记录链接的强度，也就是说，很多网络都是加权网络。文献[7]也提到，在很多情况下，可以应用无权网络中的传统方法来解决加权网络的问题。因此，将无权网络的方法拓展到加权网络是网络研究的重要问题之一。文献[8]指出，可将无权网络中的EVC扩展到加权网络，并将这样得到的加权网络EVC用于引文网络的搜索结果排序；但是，PCC作为在计算节点中心性方面比EVC更好的工具，目前还没有被扩展到加权网络。

本文首次提出将无权网络中度量节点中心性的PCC应用于加权网络，提出基于链接强度矩阵的加权主分量中心性度量法(加权PCC)。实验结果显示，加权PCC在传播效率、鲁棒性和容错性等方面优于加权EVC，因此加权PCC在加权社交网络中是可行有效的。本文最重要的贡献就是把无权网络的PCC延伸到加权社交网络，从而丰富了将无权网络经典方法拓展到加权网络的研究。

1 无权网络节点中心性计算方法

中心性常用的度量方法有度中心性、介数中心性、接近中心性[2]和特征向量中心性(EVC)[3]等。相比于其他几种中心性度量方法，EVC不仅考虑了节点的度，还考虑了邻居节点的重要性，因此成为检测社交网络中最具影响力节点的成功方法。无权网络中节点的EVC定义为：与该节点邻居的EVC之和成正比[7]。

通过分析EVC算法的收敛性得到，如果λ1为矩阵A的模最大的特征值，那么特征向量中心性x应该是与λ1对应的特征向量，也称为主特征向量[9]。从而，式(1)即为

而EVC在刻画无权网络节点中心性时，存在其缺陷[4]：最重要的一些节点集中于一个较小的区域，即EVC将最重要的一些节点视作一个小社团，而事实情况是，最重要的一些节点可能分属于不同社团；另外，大部分节点的EVC值都为无意义的0，不能充分满足排序等应用的需求。

通过将网络图映射为一个多重图，可以将无权网络节点中心性度量方法推广到加权网络；那么，加权网络中节点的EVC，为当前加权邻接矩阵的主特征向量[7]。文献[8]指出，可将这样得到的加权网络EVC用于引文网络的搜索结果排序。由于加权网络可看做无权网络映射成的多重图，EVC在刻画加权网络节点中心性时，也会存在与无权网络同样的问题。

为了弥补EVC的以上缺陷，文献[4]提出了主分量中心性(PCC)。但是目前没有研究将PCC应用于加权社交网络。于是本文拓展了无权网络的PCC，并提出了适用于加权社交网络的中心性计算模型。

2 加权网络节点中心性计算模型

2.1 链接强度矩阵

传统的中心性计算方法未能考虑节点间连接的时间动态性，而链接强度可以通过具体刻画连接可用的概率来克服这个缺陷[10]。因此，本文选用链接强度来刻画节点间链接的权重。

链接强度是定量刻画节点间链接的一种性质，由文献[11]于1973年首次提出。文献[10]认为一种关系的强度依赖于4种因素：接触频率，关系时长，接触时长，交互数目。研究者们据此提出7种因素，并根据不同的研究需要采用不同的因素来刻画链接强度：频率、亲密度、寿命、相互性、时近性、多重社交背景、信任[10]。

本文选取频率和亲密度两个因素来刻画链接强度。链路上发生的交互越频繁，越亲密(即连接时长越长)，则链接强度越强。这两个因子的计算方法是根据基于证据的策略，即用辅助性证据与反驳性证据的数目的比值来度量节点或系统对证据的信任[10]。

1) 频率因子：取决于某节点i与其他节点 j相遇的频率，用节点间相遇次数计算。

2.2 加权网络节点中心性计算模型

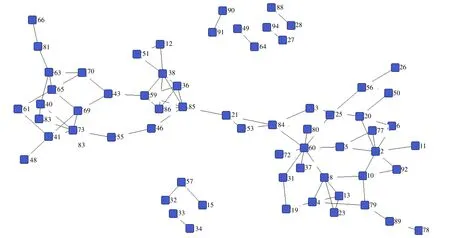
图1 M IT Reality M ining蓝牙交互网络的用户朋友关系图

3 实验与分析

3.1 实验数据集

本文选用以下3个真实的加权社交网络数据集，对加权PCC的性能进行了仿真与分析：

1) M IT Reality M ining数据集[13]：该数据集是由M IT Media Lab的Reality M ining项目经过约9个月的实验，使用104个Nokia 6600手机记录用户交互数据。本文采用其中的蓝牙交互数据，包括用户间相遇的频率、时长等数据，且选出其中94个有效用户数据进行实验。用户间朋友关系图如图1所示。用户间链接的权重根据2.1节的方法计算得到。

2) NetScience数据集[14]：这是研究网络理论与实验的1 589位科学家组成的科学家合作网。网络中的节点代表论文的作者，边是作者间的合作关系，边上的权重是根据文献[15]中的方法计算得到的。

3) Facebook-like social network数据集[16]：该数据集描述加州大学欧文分校学生的在线社会网络。它共包含1 899个节点，节点表示学生，边表示学生之间的信息接受和发送，边上的权重表示接受和发送信息的数目。该数据集本来是一个有权有向图，由于本文的中心性指标适用于有权无向图，所以本文将两个节点间接受和发送信息数目的总和作为对应链接的权重，从而将Facebook-like social network数据集转化为有权无向图进行实验。

以上3个网络数据集的相关信息如表1所示。

表1 网络数据集相关参数

3.2 传播效率分析

3.2.1 实验设置

文献[17]认为，在社交网络中信息是以串联形式进行传递，且信息串流的传播分析可用于确定社交网络中最有影响力的节点。因此，本节实验采用独立串联模型[18]来刻画社交网络的信息传播规律。基于该模型，本节实验比较加权PCC和加权EVC的传播效率，从而验证提出的加权社交网络中心性计算模型的有效性。具体的传播过程为：

1) 初始激活节点集：分别以加权 PCC和加权EVC排序得到的前N个节点为传播的初始激活节点集，分别表示为

2) 成功激活阈值：独立串联模型中，两节点v和w间存在成功激活概率pv,w；当v试图激活w时产生的随机概率小于pv,w时，v将成功激活w。将成功激活概率pv,w称为成功激活阈值(用THv,w表示)，且认为与链接强度成正比，因为链接强度越大，表明两节点关系越亲密，则两节点间传递信息越容易。设

式中，常数kÎ[0,1]称为传播参数。实验中将链接强度矩阵归一化至[0,1]，这样能保证此时，链接强度越大，THv,w越大，产生的随机概率小于THv,w的可能性越大，即节点间传递信息越容易。

3) 比较方法：当v试图激活w时产生的随机概率小于THv,w时，则v将成功激活w，信息就在两节点间传递。计算每个步骤分别以A0,PCC和A0,EVC为传播起点而被激活的节点总数，并加以比较，即可比较分别以为传播起点的传播效率。

3.2.2 结果与分析

图2是传播初始激活节点数目N取不同值时，每时刻两种加权中心性传播效率的比较。以下每幅实验结果图均是进行500次独立实验并将其结果取平均得到的。

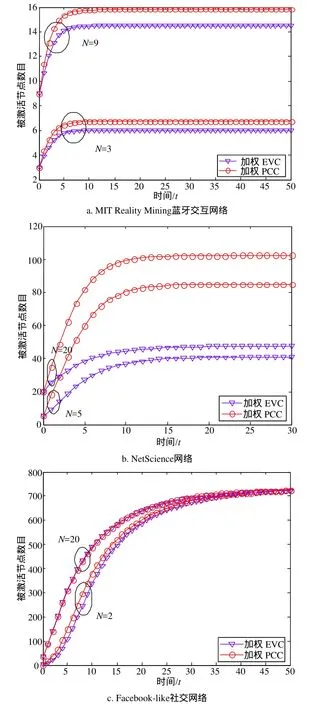
图2 加权PCC和加权EVC传播效率比较

由图2可见，在不同的加权网络中，基于加权PCC排序选出的前N位节点作为传播源的传播效率高于加权EVC，即加权PCC能更准确地识别出传播影响力高的节点。这是因为加权PCC采用了权重矩阵的更多主特征向量，能挖掘加权社交网络的更多结构信息。同时，3个加权社交网络的平均路径长度均为Inf，即3个网络均为非连通网络。可说明加权PCC由于采用了更多主特征向量，因此可以有效弥补网络非连通部分对中心性计算的影响。

另外还发现，加权PCC在高聚类系数的M IT Reality M ining数据集和NetScience网络中的优势更明显，而在聚类系数相对低的Facebook-like social network中的优势并不明显。这是因为加权PCC通过采用更多的主特征向量，能探测出加权社交网络中的主要社团结构；而低聚类系数的网络的社团特性相对不强，则加权PCC的优势相对不明显。

3.3 鲁棒性分析

社交网络中存在一类节点，它们通过关注原网络中某些用户或给它们发垃圾邮件的方式，改变原网络中某些节点的影响力[5]，称之为虚假粉丝。它们与原网络节点的互动非常微弱，即链接强度很弱，但由于改变了整个网络的结构，所以对节点中心性的计算带来了干扰。因此很有必要度量一种中心性指标针对虚假粉丝攻击的鲁棒性。

本节仿真实验令原网络中真实用户节点之间的互动关系(即链接强度)不变，同时增加20%的虚假粉丝节点。假设这些虚假粉丝节点与其他节点之间存在弱链接强度，然后比较加权PCC和加权EVC的鲁棒性，实验结果如图3所示。

图3中，y=x为比较基准，为最理想的情况，即加入虚假粉丝后，节点中心性排序不变。若加入虚假粉丝后，节点中心性排序在y=x周围波动得厉害，则说明该中心性的鲁棒性较差，反之，鲁棒性较好。由图3的结果可见，在3种加权社交网络中，加权PCC的鲁棒性均相对较好。其中，加权PCC在节点数目较少、聚类系数较高的M IT Reality M ining数据集网络中的鲁棒性最好，波动最轻微，这是因为该网络内节点间链接非常紧密，使得虚假粉丝的加入对网络性能影响较小，从而保证节点中心性排序较为稳定。在NetScience网络中，大约前440位节点的加权PCC排序保持不变，而在后面节点的排序波动也小于加权EVC。证明了加权PCC在加权社交网络中较好的鲁棒性。在Facebook-like social network中，加权PCC的鲁棒性存在一定优势，但并不明显，这是由于聚类系数较低时，外来虚假粉丝的加入较明显地改变了网络结构，使得中心性排序产生较大波动。

图3 加权PCC和加权EVC鲁棒性比较

3.4 容错性分析

中心性指标的容错性考虑的是网络增减一些伪造链接时的情况[5]。这是因为社交网络数据中可能存在噪声数据，即根据原始数据并不容易确定用户间是否存在某种链接。由于增加和移除伪造链接的容错性是对称的，本节实验针对移除伪造链接的情况进行容错性分析。检验加权中心性算法的容错性的方法是，度量当链接被随机移除时排序的变化量[5]，因为对于中心性算法，排序的准确性比中心性的具体数值更重要。噪声数据对排序的影响IR为[5]：

式中，Ri和Ri¢分别是由原图和修改后的图得到的中心性排序。

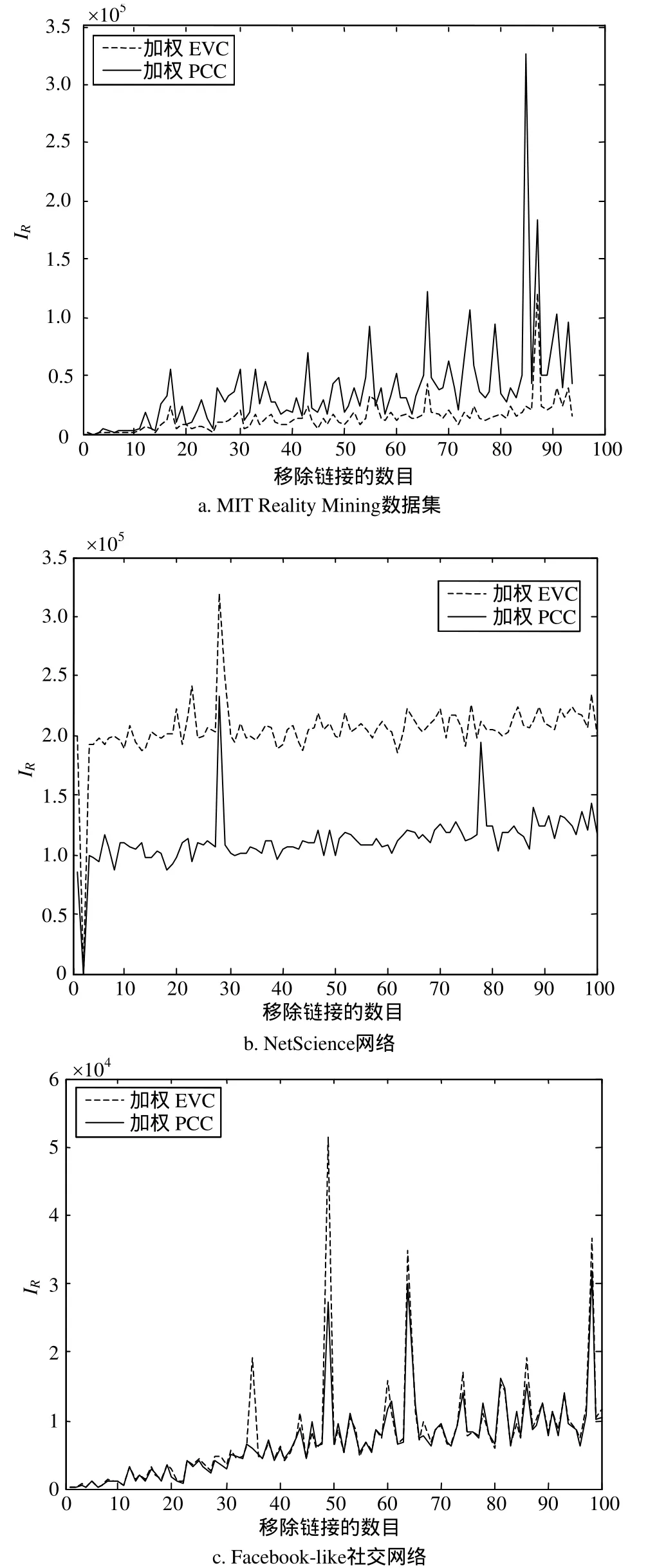
图4 加权PCC和加权EVC容错性比较

如图4所示，在NetScience网络和Facebook-like social network中，加权PCC相比于加权EVC有较小的IR，即容错性较好。而在M IT Reality M ining蓝牙交互网络中，加权PCC却表现出较差的容错性。这是因为，在M IT Reality M ining蓝牙交互网络中，我们将用蓝牙装备检测到另一个节点视为一条链接，并采用2.1节的方法计算出链接强度，这样虽能全面、准确地刻画出每两个节点间的链接强度，却同时产生了噪声数据。这使得加权PCC虽采用更多主特征向量，反而不能更好地识别噪声数据，造成容错性较差。而NetScience网络和Facebook-like social network的链接分别为节点间的合作和信息发收，均比较明确，所以数据集本身不含有太多噪声数据，因而，加权PCC容错性的优势就体现出来了。这些发现给出了启示，即本文链接强度的计算方法有待改进，如可以通过增加门限的方法，过滤掉一些噪声数据，这样能增加加权PCC的容错性。

4 结 论

确定网络中的关键节点在社交网络研究中有重要意义。本文将无权网络中度量节点中心性的方法PCC进行拓展，基于链接强度矩阵提出适用于加权社交网络的中心性计算模型(加权PCC)。实验结果显示，加权PCC在传播效率、鲁棒性和容错性比较中优于加权EVC。此结果说明，应用PCC度量并排序加权社交网络节点的重要程度，可有效地促进信息的扩散，在实际应用中很有价值，如加速信息传播、控制舆论扩散、加速移动社交网络的内容分布等。同时，由于加权PCC针对虚假粉丝有更好的鲁棒性，针对噪声数据有更好的容错性，使得它在实际加权社交网络平台中是可行有效的。

[1] WASSERMAN S, FAUST F. Social network analysis:methods and applications[M]. Cambridge, U.K.: Cambridge University Press, 1994.

[2] FREEMAN C L. Centrality in social networks conceptual clarification[J]. Social Network, 1978, 1(3): 215-239.

[3] BONACICH P. Factoring and weighting approaches to clique identification[J]. Journal of Mathematical Sociology,1972, 2(1): 113-120.

[4] ILYAS U M, RADHA H. A KLT-inspired node centrality for identifying influential neighborhoods in graphs[C]//Proceedings of the 44th International Conference on Information sciences and systems. Princeton, NJ: Princeton University, 2010: 1-7.

[5] LÜ Lin-yuan, ZHANG Yi-cheng, YEUNG C H, et al.Leaders in social networks, the delicious case[J]. PLOS ONE, 2011, 6(6): e21202.

[6] CHEN Duan-bing, LÜ Lin-yuan, SHANG M ing-sheng, et al.Identifying influential nodes in complex networks[J].Physica A, 2012, 391(4): 1777-1787.

[7] NEWMAN M. Analysis of weighted networks[J]. Physical Review E, 2004, 70(5): 56131.

[8] REDNER S. How popular is your paper? an empirical study of the citation distribution[J]. The European Physical Journal B, 1998, 4(2): 131-134.

[9] 汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 北京: 高等教育出版社, 2012: 158-166.

WANG Xiao-fan, LI Xiang, CHEN Guan-rong. Network science: an introduction[M]. Beijing: Higher Education Press, 2012: 158-166.

[10] DALY M E, HAAHR M. Social network analysis for information flow in disconnected delay-tolerant manets[J].IEEE Transactions on Mobile Computing, 2009, 8(5):606-621.

[11] GRANOVETTER S M. The strength of weak ties[J]. The American Journal of Sociology, 1973, 78(6): 1360-1380.

[12] ILYAS U M, SHAFIQ Z M, LIU X A, et al. A distributed and privacy p reserving algorithm for identifying information hubs in social networks[C]//INFOCOM.Shanghai: [s.n.], 2011: 561-565.

[13] EAGLE N, PENTLAND A, LAZER D. Inferring social network structure using mobile phone data[J]. Proceedings of the National Academy of Sciences, 2009, 106(36):15274-15278.

[14] NEWMAN M. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review E,2006, 74(3): 036104.

[15] NEWMAN M. Scientific collaboration networks II.shortest paths, weighted networks, and centrality[J].Physical Review E, 2001, 64(1): 016132.

[16] OPSAHL T, PANZARASA P. Clustering in weighted networks[J]. Social Networks, 2009, 31(2): 155-163.

[17] DOTEY A, ROM H, VACA C. Information diffusion in social media[R]. California: Stanford University, 2011.

[18] KEMPE D, KLEINBERG J, TARDOS E. Maximizing the spread of influence through a social network[C]//Proceedings of the 9th ACM SIGKDD International Conference on Know ledge Discovery and Data M ining.New York: ACM, 2003: 137-146.

编 辑 蒋 晓