无线传感器节点均匀性估计算法及其应用

宫娜娜，王缓缓

(黄河科技学院物联网传感技术及其应用郑州市重点实验室 郑州 450063)

数学物理领域从1978年开始关注分布均匀性并取得了一系列的成果。文献[1]从数论的角度研究了均匀性设计，得到了均匀设计表，与正交法相比，减少了试验次数。文献[2]根据文献[1]提出的均匀性判定准则，定义了节点间f、g距离和理想布点情况下的标准半径，由此定义了最大空穴半径和最小空穴半径，并提出了近似偏差的均匀度准则：以密集性偏差、稀疏性偏差和自偏差作为均匀度的度量测度。

考虑到锚节点均匀性对节点定位的影响，将均匀性的相关研究引入到无线传感器网络[3]。目前，关于无线传感器网络节点分布均匀性及其与节点定位之间的关系研究文献较少，研究角度和思路有如下几个方面：

1) 对均匀程度的定量描述

从概念来说，均匀程度比密度[4]和覆盖程度都复杂。文献[5]对基于偏差的均匀度描述方法进行了改进和扩充，使用锚节点之间的空隙大小和锚节点控制区域的面积大小表征锚节点分布的稀疏程度，进而定量地描述锚节点的均匀程度。

2) 均匀程度对定位精度的影响

文献[6-7]采用文献[2]中提出的方法判断均匀程度，并且在均匀程度不够的情况下，通过增大通信半径，引入更多锚节点提高均匀程度。利用最小包含圆的思想进行位置估计，有效地改善锚点不均匀带来的定位误差；但缺点是增大通信半径就无形中增大了功耗。

3) 均匀布点

文献[8]根据均匀性度量势函数模型提出均匀性布点算法，用于调节节点位置使其分布更均匀。

以上方法在均匀性判断中，均涉及距离的概念，在无线传感器网络中，需要加入测距设备，因而增加了硬件成本。

文献[6]中的最小包含圆算法以牺牲功耗换取定位精度。本文认为可以从未知节点所在区域的锚节点位置分布均匀性下手，不同区域采用不同的算法，以提高整体定位精度，避开了功耗问题。

本文所做的工作涉及均匀性的定量估计与基于该均匀性估计的定位算法两方面。因为在经典的质心算法中[9-10]，锚节点的位置越均匀，定位的误差越小，而对均匀性概念并没有做明确的定义和分析。针对这个问题，本文首先提出一种无线传感器节点的分布位置均匀性的度量方法，该方法利用接收信号强度指示RSS估计节点的相对位置，无需测距，减少了成本；然后，将该均匀性估计方法应用到定位中。在定位之前先采用该方法对区域的均匀程度做一评估，再根据区域的不同均匀程度采用不同的定位算法，即混合定位算法，以提高整体定位精度。从而克服文献[6]中通过增大通信半径提高定位精度的功耗问题，并且减少了计算复杂度。

1 均匀性估计算法原理

1.1 节点的中心对称性

研究以未知节点为圆心，其通信半径为半径的圆内锚节点的分布情况，该分布情况对定位精度有很大的影响。在这个圆形区域中，一种最简单、最理想的均匀性可理解为各个锚点与未知节点距离相等，且相邻锚节点的距离也相等，即各锚节点分布在以未知节点为圆心的圆上，只是该圆的半径要小于通信半径，如图1a所示，锚节点b1～b8均匀分布在未知节点N周围。关于各点的位置关系有下列定理。

利用图1a中8个锚节点信息，对未知节点N的定位结果必然是N本身，这时的定位是完全准确的。实际上，并不需要各锚节点之间的距离均相等，只要所有的锚节点关于未知节点均两两中心对称的，其横纵坐标的代数平均值，即质心必然是圆心，这时定位也没有误差。

1.2 均匀性估计的基本思想

若从质心算法的定位误差来考虑均匀性，应该与锚节点相互之间的距离无关，而与锚节点和未知节点的相对位置关系有关。从该角度来说，判断均匀性就可以从锚节点与未知节点的相对位置出发。图1a为锚节点均匀分布图，在进行均匀性估计时，把实际中的节点分布与其相比，将两者的差别作为均匀性的衡量指标。显然差别越大，均匀性越差。从哪种角度衡量两者差别需要重点研究。

经分析，对于图1a，若未知节点向各方向移动，图中虚线圈内的箭头所示，其靠近和远离的锚节点数目是相同的，均为4个。换句话说，若未知节点周围的锚节点分布较均匀，则未知节点移动后，靠近和远离的锚节点数目相差不大；反之，若锚节点分布不均匀，则一侧较多，另一侧较少，如图1b所示。即未知节点移动后，必然在某些方向上远离和靠近的锚节点数目相差较大。因此，提出以远离和靠近锚节点个数差为线索的估计均匀性的思路。一种极限情况是两者数目相等，个数之差为0，这时最均匀；另一种极限情况是全部靠近或者远离，则个数差(绝对值)最大，等于锚节点总个数。为了进行统一的比较，将这种个数差进行归一化，即除以总的锚节点个数和方向个数之积。

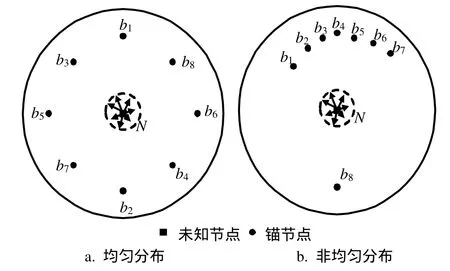
图1 锚节点分布示意图

在实际实现时，有两个主要问题需解决：

1) 节点一般是静态的，不能运动；

2) 移动方向不能穷尽。

参考APIT算法[11-13]的思想，借助邻居节点模拟节点的运动，只是一个均匀性的估计，需要较高的节点密度。这样，移动方向个数也是有限的，可以进行归一化。另外，锚节点的远离和靠近由接收信号强度(RSS)确定[14-17]，无需额外硬件。

1.3 成立条件的讨论

上述均匀性估计的讨论，是有一定条件的，这与未知节点的移动幅度和方向有关。本文研究在以下前提下进行的。

1) 未知节点的移动幅度

幅度应较小，尽可能在锚节点集合的外部移动。移动幅度较大时，有可能移进某些锚节点集合内部，或是从某些锚节点集合移出，造成OutToIn或者InToOut错误。如图2a中箭头所示，未知节点N从圆心移到位置1，对于b1,b3,b5,b7是靠近的；从圆心移到位置2时，对于b1是远离的，对于b3,b5,b7是靠近的，这属于OutToIn错误；从圆心移到位置3时，对于b1和b7是远离的，对于b3和b5是靠近的，这包含OutToIn和InToOut两种错误。

2) 未知节点移动的方向

移动方向不应与两锚节点的连线垂直，如图2b中b1和b2与N共线，按照位置1的方向移动，与b1和b2的连线相垂直，这时远离b1,b2,b4,b6,b8，靠近b3,b5,b7。导致远离与靠近的锚节点数量不相同。

图2 影响因素

2 均匀性估计算法流程

设锚节点的通信半径为R1，未知节点的通信半径为R2，为保证在未知节点的通信区域中，也就是半径为R2圆内的未知节点均能收到锚节点发送的数据，要求R1≥2R2。以未知节点为研究对象，研究其通信范围内锚节点分布的均匀性。均匀性估计算法的具体步骤如下：

1) 建立信息表

首先，锚节点发送数据包含自身的ID和位置，在其通信半径R2圆内的未知节点均能接收数据。收到数据后，未知节点记录锚节点的ID及相应的RSS值，建立自身的锚节点信息表X1；然后，未知节点发送数据，包含自身的ID，接收数据的节点包含锚节点与未知节点两种类型。节点接收到数据后，记录下ID及相应接收信号的RSS值，并将其反馈给发送数据的未知节点。未知节点根据反馈信息，记录锚节点的ID、位置及接收信号RSS值，建立自身的锚邻居信息表X2；记录未知节点的ID及接收信号RSS值，建立自身的未知节点信息表X3。

显然，若锚节点的通信半径与未知节点的通信半径相等，即R1=R2，此时X1=X2；而对于R1>2R2，锚节点信息表X1应包含锚邻居信息表X2中的信息。

2) 确定未知邻居

为减少OutToIn或者InToOut错误，选择未知节点要缩小范围。首先，由锚邻居信息表X2，根据RSS值最大原则，找出距离自己最近的锚节点；在未知节点信息表X3中，找出比最近的锚邻居RSS值更大的未知节点，作为未知邻居，建立未知邻居信息表X4，包含ID及相应的RSS值。

3) 考查未知邻居

根据未知节点的锚邻居信息表X2中的信息，依次考查未知邻居信息表X4中各未知邻居的锚节点信息表X1，找出与X2对应的相同ID号的锚节点RSS值。若RSS增大，则说明此未知邻居比该未知节点离锚节点要近；否则，要远。依此确定每个未知邻居远离或靠近的锚节点个数。

4) 计算归一化均匀性偏差NUD

设总的锚邻居个数为m，未知邻居节点个数为n，设第i个未知邻居与未知节点本身相比，远离的锚节点个数为mi1，靠近的个数则为mi2=m-mi1。那么，归一化均匀度偏差(normalized uniformity discrepancy,NUD)为：

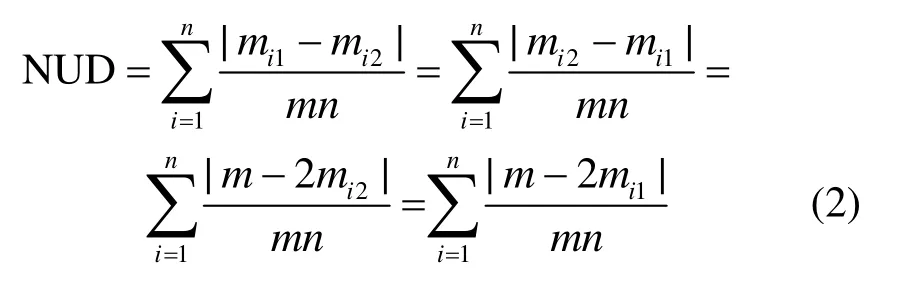
式中，当mi1= mi2时，即远离与靠近锚节点个数相同，NUD=0，最均匀；当mi1或mi2有一个等于0时，即全部远离或全部靠近，NUD=1，最不均匀。

3 均匀性估计算法验证

在100 m´100 m的区域中仿真，随机产生若干个未知节点和锚节点，然后随机选择一个未知节点的通信区域作为研究区域。锚节点的通信半径R1=60 m，未知节点的通信半径R2=30 m。

3.1 主观验证

经过3次仿真实验，分别求得3个区域的节点分布和NUD，如图3所示。可见，越均匀，NUD值越小。

图3 3种不同的分布情况

3.2 客观验证

结合质心算法的定位误差大小，从客观上验证该算法的有效性。因为在一般情况下，区域中的锚节点越不均匀，质心算法定位误差越大，归一化均匀性偏差NUD越大。随机选取10个区域NUD值与定位误差值的计算结果进行分析比较，如表1所示，随着NUD值的增大，即越不均匀，定位误差也逐渐增大，即均匀性高的锚节点分布，其定位精度越高，从而验证了该方法得到的均匀性度量指标是有效的。

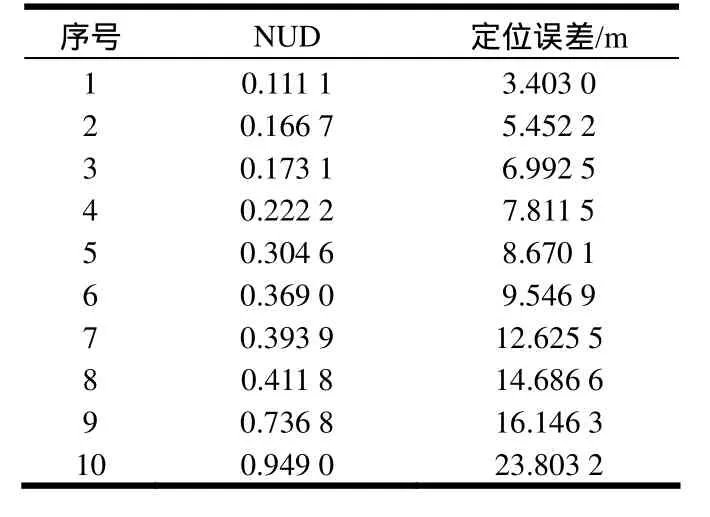
表1 均匀性与定位误差

4 基于均匀性估计的混合定位算法

最小包含圆的定位算法[6]是找出包含邻居锚节点的最小圆，将其圆心作为未知的估计值。与质心定位算法相比，它对锚节点分布的均匀性要求不高，更适于锚节点分布不均匀的场合，其算法的复杂度比质心算法高很多，因质心算法的运算复杂度是O(n)，而采用暴力算法的最小包含圆的运算复杂度是O(n4)。并且，在均匀程度不够时，它依靠增大通信半径提高均匀程度，从而提高定位精度，必然增加功耗，其本质是以功耗换取定位精度，而本文以定位算法的选择来提高定位精度。因此，综合质心算法和最小包含圆算法的特点，提出如下的混合定位算法：

1) 应用上述均匀性估计方法，对每个未知节点的区域进行均匀性评价，计算出相应的NUD值。

2) 设定NUD阈值，对于NUD值小于该阈值的区域，相对均匀，采用质心算法，定位精度高，而且算法复杂度小；而NUD值大于该阈值的区域，相对不均匀，采用最小包含圆算法，以提高定位精度。

该算法与文献[6]相比，在一定程度上提高了定位精度，减少了算法复杂度。

5 混合定位算法的仿真与分析

对于NUD值不同的区域，采用不同的定位算法，定义精度是不同的，仿真效果如图4所示。图4a为区域1，NUD=0.093 3，锚节点分布相对均匀，质心算法的误差为0.374 9 m，最小包含圆算法的误差为5.246 4 m；图4b为区域2，NUD=0.303 6，锚节点分布相对不均匀，质心算法的误差为12.300 4 m，最小包含圆算法的误差较小，为4.933 9 m。所以，对于具有这种特点的两种区域，应分别采用质心算法和最小包含圆算法。

随机选择10个区域进行定位，设定阈值为0.18，得到3种算法的定位误差数据如图5所示。其中，质心算法的平均误差为7.548 9 m，最小包含圆算法平均误差为5.760 8 m，混合定位算法误差为4.479 9 m。混合算法对于质心算法的定位精度提高了40.65%，对于最小包含圆的定位精度提高了22.23%。可见，混合定位算法有效地提高了定位精度。

图4 质心算法与最小包含圆算法的定位效果比较

图5 3种算法定位误差比较

下边讨论不同参数对定位精度和功耗的影响，并对3种算法的计算复杂度进行分析。

5.1 阈值的选取对定位精度的影响

对于图5中的10个区域，变换不同的阈值，进行混合算法的仿真，得到定位误差的结果如表2所示。可以看出文中阈值选择0.18是比较合适的，阈值选取得过大或过小，都会增大定位误差。

表2 阈值对定位误差的影响

5.2 锚邻居与未知邻居对定位精度和功耗的影响

对图5中的10个区域，统计节点的锚邻居、未知邻居个数如表3所示。

表3 锚邻居、未知邻居个数

锚邻居的个数对于3种算法的定位精度一般影响不大，但其分布均匀情况会影响定位精度，其质心算法比最小包含圆算法对于均匀程度更敏感。未知邻居不影响质心算法和最小包含圆算法的定位精度，但是对于混合算法，由于未知邻居的个数及分布情况，会影响归一化均匀性偏差NUD值的计算，进而影响阈值的选择，最终影响定位的精度。

从功耗方面分析，锚邻居与未知邻居节点个数越多，节点间通信越多，功耗越大。单个节点分析，锚节点的通信半径比未知节点大，功耗也会大一些。

5.3 3种算法计算复杂度的分析

显然，混合算法的计算复杂度处于质心算法与最小包含圆算法之间。从这个意义来说，与质心算法相比，混合算法可以说是牺牲算法的复杂度换取定位精度；而与最小包含圆算法相比，混合算法既减小了复杂度，又提高了定位的精度。

6 结 论

本文提出混合定位算法的中心思想是根据区域的不同均匀程度，采用不同算法，以从整体上提高定位精度。为此，首先，采用归一化均匀性偏差NUD值定量评估锚节点分布的均匀性，无需测距，成本较低。另外在均匀性估计过程中建立包含锚节点的位置信息，可以直接用于定位；并以此为基础，利用质心算法和最小包含圆算法进行混合定位，有效地提高了定位精度。

在定位中，均匀性度量NUD阈值的设定，会影响到定位精度，如何通过尽可能简单的方法得到有效阈值，有待进一步的研究。

本文研究工作得到了郑州市物联网信息技术科技创新项目(112PCXTD343)和郑州市智能图像处理与识别重点实验室的支持，在此表示感谢！

[1] 方开泰. 均匀设计——数论方法在试验设计中的应用[J].应用数学学报, 1980, 3(4): 363-372.

FANG Kai-tai. Uniform design-application of number theory in pbibd[J]. Acta Mathematicae Applicatae Sinica,1980, 3(4): 363-372.

[2] 胡东红, 李德华, 王祖喜. 均匀性度量中的密集性偏差与稀疏性偏差[J]. 数学物理学报, 2002, 22(1): 128-134.

HU Dong-hong, LI De-hua, WANG Zu-xi. New measurements of uniformity-compression discrepancy and sparseness discrepancy[J]. Acta Mathematica Scientia. 2002,22(1): 128-134.

[3] ZHU Gui-bin, ZHANG Hai-cheng, YE Jiu-zhi, et al. An anchor-free position algorithm for evenly deployed w ireless sensor networks[C]//2011 Third International Conference on Measuring Technology and Mechatronics Automation.Shanghai: IEEE Computer Society, 2011: 379-382.

[4] 韩金枝. 基于节点密度的无线传感器网络分区域节点定位技术研究[D]. 西安: 西北大学, 2012.

HAN Jin-zhi. Research on node localization based on node density for w ireless sensor network[D]. Xi’an: Northwest University, 2012.

[5] 周全, 朱红松, 罗海勇, 等. 无线网络节点的均匀性度量[J]. 高技术通讯, 2010, 20(5): 448-453.

ZHOU Quan, ZHU Hong-song, LUO Hai-yong, et al. A uniform ity metric for w ireless sensor networks[J]. Chinese High Technology Letters, 2010, 20(5): 448-453.

[6] 周全, 朱红松, 徐勇军, 等. 基于最小包含圆的无线传感器网络定位算法[J]. 通信学报, 2008, 29(11): 84-90.

ZHOU Quan, ZHU Hong-song, XU Yong-jun, et al.Smallest enclosing circle based localization approach for w ireless sensor networks[J]. Journal on Communications,2008, 29(11): 84-90.

[7] ZHOU Quan, LI Xiao-wer, Xu Yong-jun. Smallest enclosing circle based localization approach for w ireless sensor networks[C]//Proceedings of 2009 WRI International Conference on Communications and Mobile Computing.Kunm ing: IEEE, 2009: 61-65.

[8] 张玲, 张胜兰, 艾君, 等. 基于势函数的均匀性度量与均匀性布点方法[J]. 湖北大学学报(自然科学版), 2007,29(2): 144-146.

ZHANG Ling, ZHANG Sheng-lan, AI Jun, et al. Uniform measurement and uniform dots distribution based on potential function[J]. Journal of Hubei University(Natural Science) , 2007, 29(2): 144-146.

[9] BULUSU N, HEIDEMANN J, ESTRIN D. GPS less low cost outdoor location for very small devise[J]. IEEE Personal Communications Magazine, 2000, 7(5): 28-34.

[10] 何艳丽. 无线传感器网络质心定位算法研究[J]. 计算机仿真, 2011, 28(5): 163-166.

HE Yan-li. Research on centroid Localization algorithm for w ireless sensor networks based RSS[J]. Computer Simulation, 2011, 28(5): 163-166.

[11] HE T, HUANG C, BLUM B M, et al. Range-free localization schemes for large scale sensor networks[C]//Proceedings of the 9th Annual International Conference on Mobile Computing and Networking. New York, NY, USA:ACM, 2003: 81-95.

[12] 戴佩华, 薛小平, 邵玉华. 基于垂直平分线的区域定位算法[J]. 计算机工程, 2009, 35(2): 105-108.

DAI Pei-hua, XUE Xiao-ping, SHAO Yu-hua. M idnormalbased area localization algorithm[J]. Computer Engineering, 2009, 35(2): 105-108.

[13] 万国峰, 钟俊. 基于三角形理论的无线传感器网络定位算法[J]. 计算机应用研究, 2013, 30(1): 249-251.

WAN Guo-feng, ZHONG Jun. Triangle-based localization algorithm for w ireless sensor networks[J]. Application Research of Computers, 2013, 30(1): 249-251.

[14] 任重远. 基于RSS技术的无线传感器网络定位方法研究[D]. 上海: 上海交通大学, 2012.

REN Zhong-yuan. Research of RSS Technology Based Localization Method in Wireless Sensor Networks[D].Shanghai: Shanghai Jiaotong University, 2012.

[15] 王缓缓, 胡爱娜. RSS和距离区间映射的测距方法[J]. 电子科技大学学报, 2012, 41(4): 522-526.

WANG Huan-huan, HU Ai-na. Ranging method based on the mapping between RSS and distance scope[J]. Journal of University of Electronic Science and Technology, 2012,41(4): 522-526.

[16] HUANG Wei , ZHANG Zhen-hua, WANG Ri-bin, et al. An adaptive distance correction localization algorithm based on RSS for WSNs[J]. Lecture Notes in Electrical Engineering, 2012, 143(1): 369-378.

[17] FENG Wen-jiang, BI Xiao-wei, JIANG Rong. A novel adaptive cooperative location algorithm for w ireless sensor networks[J]. International Journal of Automation and Computing, 2012, 9(5): 539-544.

编 辑 张 俊