WLAN M IMO-OFDM系统DSAP设计与实现

朱勇旭，易芝玲，吴 斌，周玉梅

(1. 中国移动研究院 北京 西城区 100053; 2. 中国科学院微电子研究所 北京 朝阳区 100029)

M IMO检测器是多输入多输出和正交频分复用(M IMO-OFDM)系统中最为核心的模块。在检测过程中常利用QR分解将检测问题转换为树形结构的星座点搜索，可取得性能和复杂度的平衡[1-2]。矩阵的QR分解常用的3种方法是：修正格拉姆-施密特(modified Gram-Schmidt，MGS)正交化方法[3]、Householder变换法和Givens旋转法。Givens旋转法采用协调旋转数字计算(CORDIC)运算实现Givens旋转[4]，通过多次Givens旋转达到矩阵的QR分解目的，在实现上，脉动阵列是常用实现结构，无需复杂乘法、除法和开方等运算，具有结构规则和扩展性强等特点。

无线局域网(WLAN)802.11n/ac协议规定支持2´2到8´8天线配置，支持20/40/80/160 M带宽，需要对QR分解模块进行可配置设计以支持不同天线维数和子载波数(不同带宽对应不同子载波数)。WLAN通信系统需要进行ACK反馈机制，规定反馈时间不能超过16 μs。根据这些应用需求，本文对传统的串行脉动阵列处理器(serial systolic array processor,SSAP)进行改进[5]，提出一种分布式脉动阵列结构。通过对分布式脉动阵列的分析和验证，该结构相对于已有的设计在处理延时、天线数和子载波数可扩展性、资源开销方面均有较优越的性能。

1 QR分解及脉动阵列

M IMO-OFDM系统频域复数模型可表示为：

式中，s(k)为发送复数信号矢量；r(k)为接收复数信号矢量；h(k)为复数信道矩阵；n(k)为复数白噪声矢量，其中k为子载波序号。

在实现上，常采用脉动阵列结构实现上述QR分解过程，如图1所示，其中圆形是边界单元，正方形是内部单元。边界单元工作于CORDIC运算向量模式，将信道元素组成的向量旋转至x轴，实现元素消零并向右输出旋转角度；内部单元工作于CORDIC运算旋转模式，根据输入角度对向量进行旋转，并向下输出旋转后向量虚部和向右传递输入角度。左边的上三角阵列用于计算R矩阵，其输入是列延时后的信道矩阵，右边的方阵用于计算Q矩阵，其输入是列延时后的单位阵。脉动阵列结构处理过程可参考文献[6]。

图1 QR分解的脉动阵列

2 WLAN系统特点及分布式脉动处理算法

2.1 WLAN系统特点

WLAN系统利用不同天线流上接收到的长训练序列进行信道估计，然后将估计得到信道矩阵H送入QR矩阵分解模块，经过一定矩阵分解延时后，得到的分解矩阵Q和R将存入Q和R矩阵存储器中，再根据数据OFDM符号中子载波号读取与其对应的Q和R矩阵，进行M IMO处理得到检测信号，其中，QR分解的延时会直接增加系统延时，如图2所示。文献[5]采用的串行脉动阵列处理器结构中，下一子载波必须等前一子载波分解完毕才能输入，造成更大延时，其延时随子载波数线性增加，在80 MHz工作频率下对52个子载波(20 MHz带宽)信道系数进行QR分解的延时是57.2 s，即4 576个时钟周期，远超出了WLAN协议规定的反馈时间16 s。在WLAN的40/80/160M带宽模式下，其延时将进一步增加。

2.2 分布式脉动阵列处理算法

对于不同天线配置，只需要扩展图2所示的脉动阵列。为了解决传统串行脉动阵列中处理延时随子载波数线性增加的问题，文献[6]提出了分布式脉动阵列处理算法，其中分布式脉动阵列处理算法的核心思想包含以下两部分：

1) 采用新的信道系数输入规律，改变传统的子载波串行输入方式，对不同子载波信道矩阵系数进行分组交织处理后输入脉动阵列。

2) 进行脉动阵列的分布式计算。将分组交织后的信道矩阵按照列延时方式输入脉动阵列，脉动阵列中边界单元和内部单元CORDIC采用流水线计算后，不同子载波信道矩阵的QR分解将分布于脉动阵列中CORDIC流水线运算的不同级。由于边界单元和内部单元流水线级数均是T，而且同一子载波信道系数相邻行以间隔T个周期输入脉动阵列，所以同一子载波信道矩阵在脉动阵列中进行QR分解过程里，每隔T个时钟周期将与本子载波下一行的信道系数相遇，组成的向量在边界单元和内部单元进行CORDIC向量模式和旋转模式的流水线计算。在保证每个子载波QR分解完成的同时，实现不同子载波信道矩阵的QR分解分布于脉动阵列CORDIC流水线的不同级，该方式充分利用了脉动阵列的流水线特性，时间利用率可达到100%，有效减小了处理延时，适合WLAN通信系统应用。

图2 WLAN系统M IMO检测过程

3 分布式脉动阵列结构

3.1 整体结构

分布式脉动阵列处理器架构如图3所示，用于M´M的实数信道矩阵的QR分解。图中圆形单元是脉动阵列的边界单元，方形单元是脉动阵列的内部单元，均采用流水线设计，级数均为T。

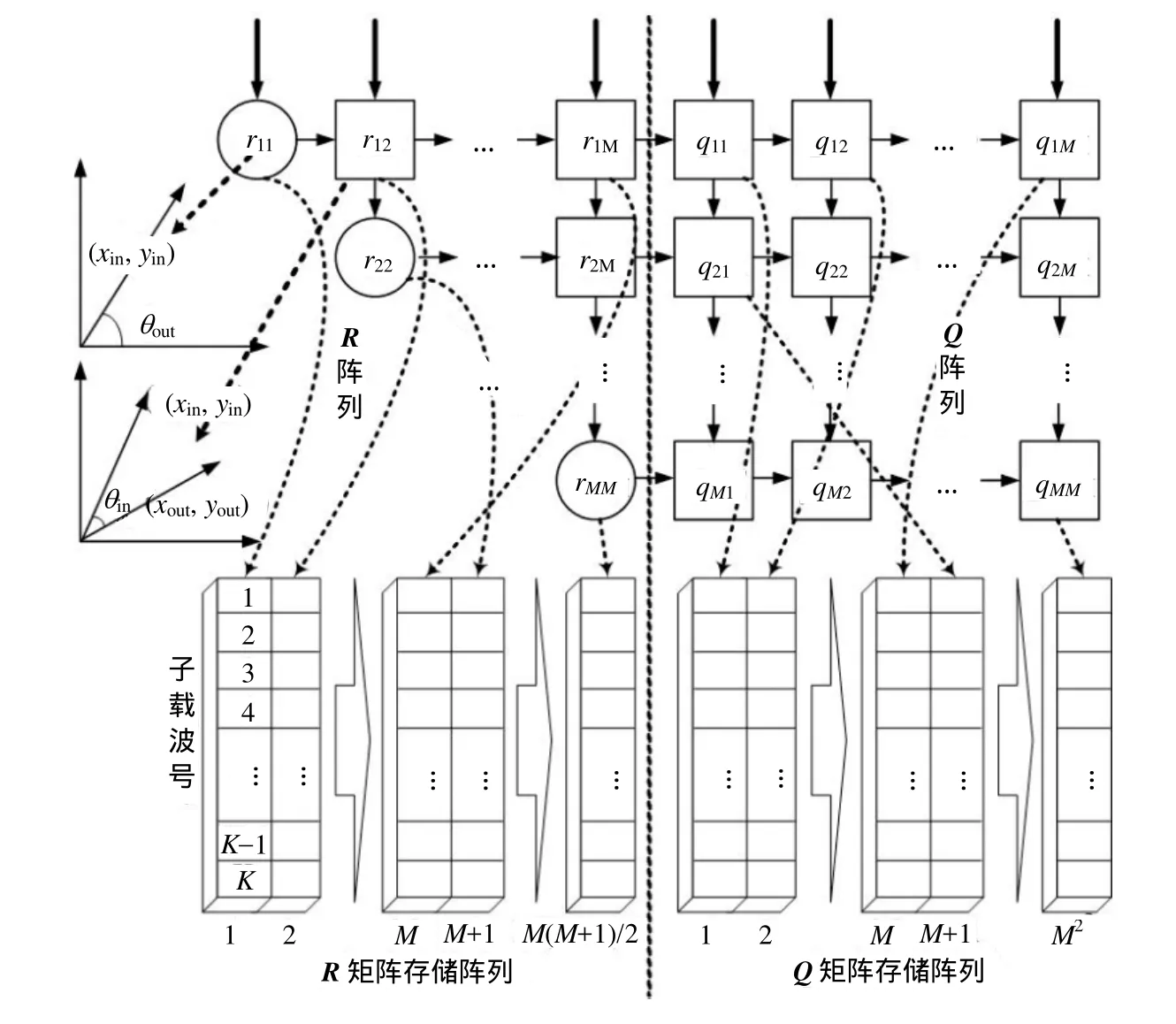
图3 分布式脉动阵列处理器架构

3.2 边界单元和内部单元CORDIC流水线结构

如图4所示，图a是边界单元CORDIC流水线结构，图b是内部单元CORDIC流水线结构。

图4 CORDIC流水线结构

4 FPGA和ASIC实现及结果分析

本文设计采用Verilog HDL描述。首先，使用ModelSim仿真工具进行功能验证；然后，对设计进行FPGA综合并将其加入基于FPGA的2发2收802.11n原型系统中进行系统级验证，通过WLAN专用测试设备IQNXN进行测试，能正确解调发射的数据帧。将通过FPGA验证的2发2收802.11n系统进行ASIC实现，设计了2发2收数模混合M IMO-OFDM SoC，采用SM IC 0.18 mm CMOS工艺，芯片面积为37.5 mm2(7.5 mm´5.0 mm)，如图5所示。采用QFP-176封装，SoC中集成4路ADC、4路DAC和数字基带(面积为19.2 mm2)，支持802.11a/g/n协议，支持20 MHz带宽和52个数据子载波。其中M IMO检测器采用QR-ZF算法，QR分解采用提出的分布式脉动阵列处理器结构，QR-ZF检测器的面积为5.76mm2(其中QR分解面积为3.86 mm2)。图6是通过FPGA验证的2发2收802.11n系统，采用130 Mb/s数据率进行高清视频同步传输。

图5 2发2收M IMO-OFDM SOC

图6 2发2收M IMO-OFDM SoC系统演示图

1) 资源开销分析

表1是使用A ltera Stratix II EP2S180对2´2 802.11n系统芯片进行FPGA综合得到的基带整体资源和QR-ZF检测器资源开销。作为基带芯片中主要的计算模块，分布式脉动阵列预处理单元占用了47%的计算逻辑资源和43%的寄存器资源。本文设计采用全CORDIC计算，避免了复杂的除法、乘法、开方，在资源开销上得到有效减小。

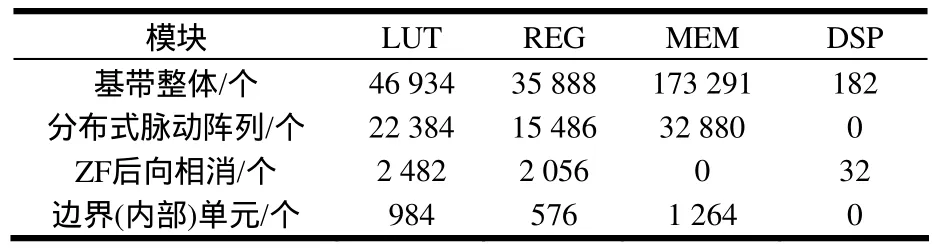
表1 2发2收802.11n基带处理器主要模块硬件开销

2) 延时分析

分布式脉动阵列将进行56个子载波QR分解，从信道系数输入到56个子载波分解处理完成共需要270个时钟周期，在80 MHz工作频率下延时大小为3.375 μs，每个子载波处理平均延时是4.8个时钟周期，而实际每个OFDM符号是320个时钟周期，在数据OFDM符号来时，信道估计和信道系数QR分解预处理已经完成，无需进行缓存处理。与文献[7-9]相比，在延时上均有很大优势。

3) 天线可扩展性分析

采用脉动阵列结构的QR分解单元有很好的天线可扩展性。根据天线数，直接扩展相应数目的边界单元和内部单元就可构造不同天线配置下的脉动阵列。在3´3天线配置下(实数信道矩阵是6´6)，脉动阵列左边是6´6的上三角阵，6个边界单元分布于对角线，上三角阵中其余位置均是内部单元，右边是由内部单元组成的6´6的方阵。在其他天线配置下，可依此规律构造。

5 结 束 语

IEEE 802.11n/ac协议的产品设计及SoC研究实现成为产业和学术界的关注热点，低延时、低复杂度及可扩展性的QR分解预处理器是WLAN接收机中核心部分。本文提出的分布式脉动阵列处理结构有效解决了QR分解预处理器的延时大、复杂度高及扩展性差的问题，该结构的延时是传统串行脉动阵列的8%，避免了大量复杂的乘法、除法及开方等运算，对于具有不同子载波数和天线维数的QR分解，只需扩展脉动阵列的维数即可。此外，本文的分布式脉动阵列思想可扩展至LTE、802.16d/e等通信系统中，具有较好的参考和实用价值。

[1] KIM T H, PARK I C. Small-area and low-energy K-best M IMO detector using relaxed tree expansion and early forwarding[J]. IEEE Transactions on Circuits and Systems-I:Regular Papers, 2010, 57(10): 2753-2761.

[2] SHEN C A, ELTAWIL A M. A radius adaptive K-best decoder w ith early termination: Algorithm and VLSI architecture[J]. IEEE Transactions on Circuits and Systems-I:Regular Papers, 2010, 57(9): 2476-2486.

[3] HUANG Z Y, TSAI P Y. Efficient implementation of QR decomposition for gigabit M IMO-OFDM systems[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers,2011, 58(10): 2531-2542.

[4] MA L, DICKSON K, MCALLISTER J. QR decompositionbased matrix inversion for high performance embedded M IMO receivers[J]. IEEE Transactions on Signal Processing,2011, 59(4): 1858-1867.

[5] HAENE S, PERELS D, BURG A. A real-time 4-stream M IMO-OFDM transceiver: system design, FPGA implementation, and characterization[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(6): 877-889.

[6]朱勇旭, 吴斌, 周玉梅, 等. 用于M IMO-OFDM系统QR分解的分布式脉动阵列处理算法[J]. 电子与信息学报, 2012,34(8): 1968-1973.

ZHU Yong-xu, WU Bin, ZHOU Yu-mei, et al. A distributed systolic array processing algorithm for QR-decomposition in M IMO-OFDM system[J]. Journal of Electronics&Information Technology, 2012, 34(8): 1968-1973.

[7] CHANG R, LIN C, LIN K, et al. Iterative QR decomposition architecture using the modified Gram-Schmidt algorithm for M IMO systems[J]. IEEE Transactions on Circuits and Systems I: Regular Papers,2010, 57(5): 1095-1102.

[8] CHEN D D, SIMA M. Fixed-point CORDIC-based QR decomposition by givens rotations on FPGA[C]//International Conference on Reconfigurable Computing and FPGAs (ReConFig). Cancun, Mexico: [s.n.], 2011.

[9] HWANG Y T, CHEN W D. Design and implementation of a high-throughput fully parallel complex-valued QR factorisation chips[J]. IET Circuits Devices Systems, 2011,5(5): 424-432.

编 辑 张 俊