OFDM系统中的峰值抵消频域噪声分布特性研究

肖 悦，何 旭，冀秋月，马千里，李少谦

(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)

正交频分复用(OFDM)是一种高频谱利用率的多载波调制技术[1]，它具有良好的对抗频率选择性衰落的能力，近年来成为无线通信系统的候选技术之一。但是，多个统计独立的子载波经过OFDM调制后时域信号会存在较大的峰值，造成高峰均功率平比(PAPR)问题。较高的PAPR信号在通过功率放大器时会产生频谱扩展和严重的带内失真，造成子信道间的相互干扰，从而影响OFDM系统的性能。

在现有文献中，已经有大量技术和方法[2-3]用于降低OFDM系统的PAPR。在这些方法中，峰值消除算法[4-5](peak cancellation, PC)以其有效的PAPR控制能力和较低的计算复杂度受到普遍关注。该方法将OFDM信号与特定的抵消信号加权叠加，达到削弱高峰值点的目的。不同于限幅滤波算法，峰值抵消方法选择频域窗函数作为基本抵消信号单元，通过窗函数选择控制抵消噪声分布，并可通过时域截断窗长近一步降低计算复杂度。因此，在峰值抵消过程中该方法不需要额外滤波操作，且计算复杂度低。但是，基于窗函数的峰值抵消过程将引入抵消噪声。已有相关文献对峰值抵消过程的信号衰减和噪声功率进行了研究。文献[6-8]分析了基于脉冲函数的峰值抵消法-限幅滤波的噪声分布及功率估计。文献[9]分析了基于矩形窗函数的峰值抵消信号与数据信号的相关特性，并推导了不同门限下的峰值抵消噪声总功率。上述分析都假设抵消后信号噪声的带外功率泄露可忽略，因此其信号抵消噪声功率比可等效为信号带内干扰比。但实际截断窗函数或过渡带的窗函数(如高斯窗)都将引起噪声频谱展宽，引起带外噪声泄露及各子载波上噪声功率差异[10]。如何预计峰值抵消过程的频域噪声分布对相邻信道干扰估计及接收端噪声去除都至关重要[11-12]。

该文针对正交频分复用系统中基于非理想窗函数的峰值抵消过程，分析了抵消信号的频域功率分布特性。与现有抵消噪声估计方法相比较，基于本文推导的频谱噪声能更好的进行噪声恢复，并提高接收端性能。

1 以往研究结果

1.1 系统模型

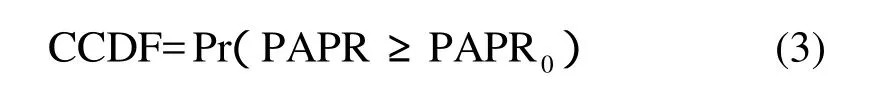
根据中心极限定理可知，当子载波数较高时，OFDM时域信号近似为一个复高斯信号，其功率分布服从2c分布。在奈奎斯特采样率下，OFDM符号周期内各采样值之间是不相关的。这种情况下，OFDM信号的CCDF为：

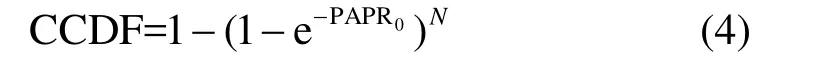
在过采样情况下(过采样因子率J≥3)，各采样点不再满足统计独立的要求。此时可根据信号击穿率，得到一个渐近的OFDM信号的CCDF表达式[8]：

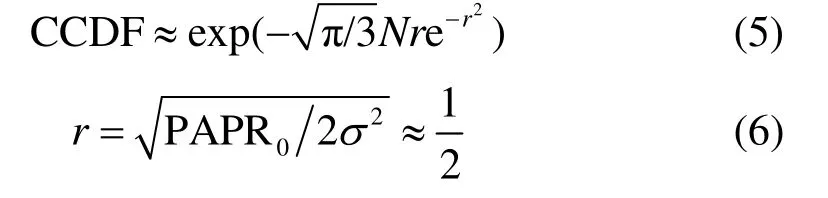
式中，2s表示OFDM符号的方差。本文统一采用CCDF作为PAPR的衡量参数。

1.2 峰值抵消算法及时域噪声功率

峰值抵消法[5]选取带宽受限的频域窗函数作为抵消函数，因此不会引入带外辐射。如图1所示，该方法发送端的处理步骤如下：

1) 频域信号通过JN阶的IFFT变换，得到时域信号sn。

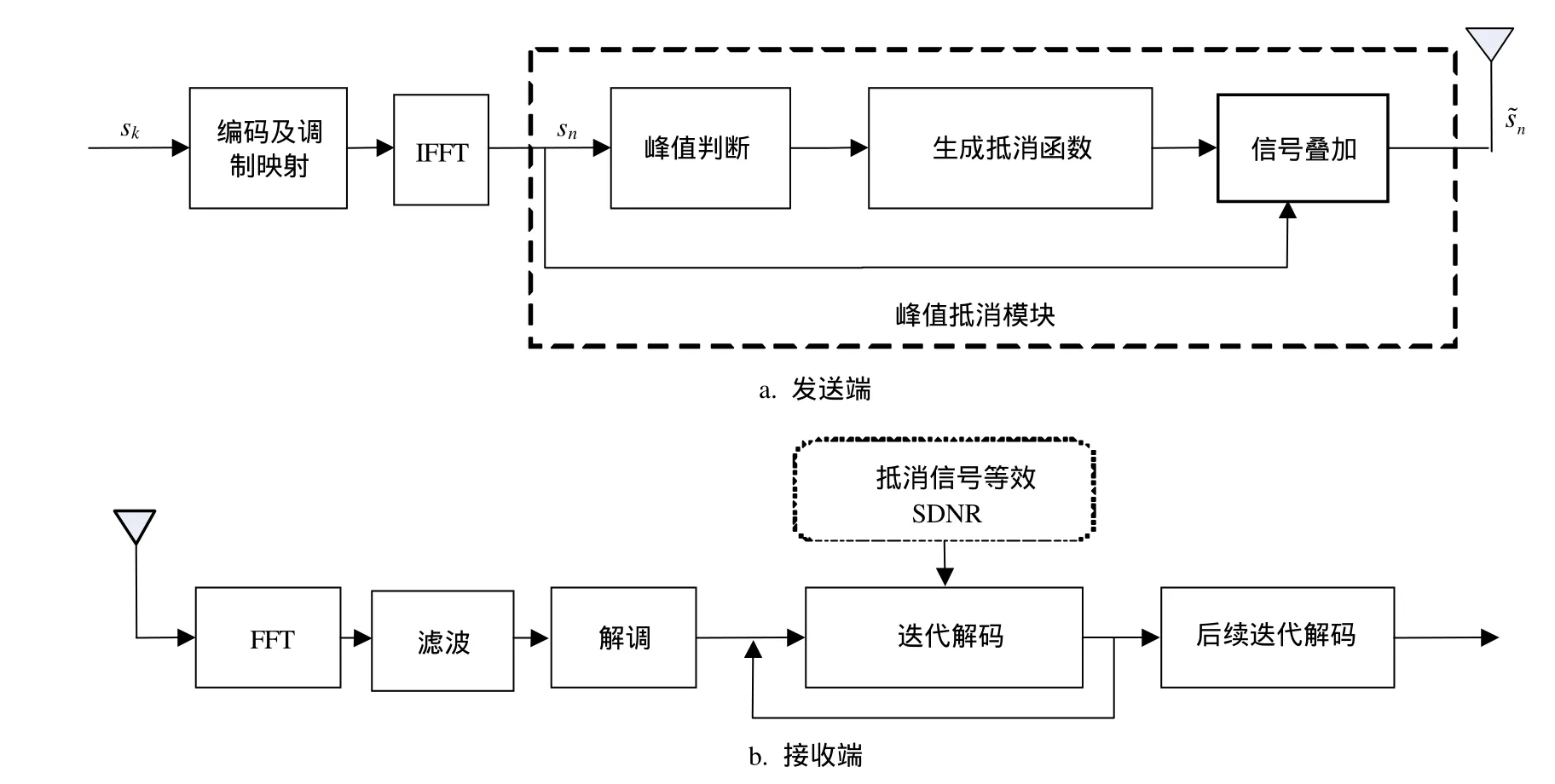
图1 串行峰值抵消OFDM系统框图

2) 将时域信号sn与预设门限A作比较，生成各信号点的加权因子An：

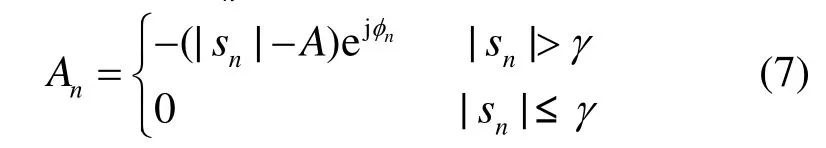
3) 根据加权因子，生成对应抵消函数，并叠加生成时域抵消信号为：

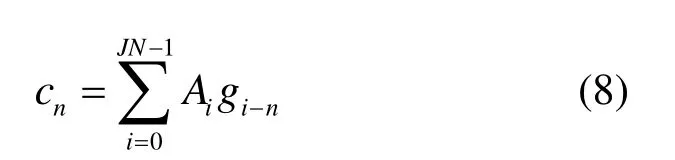
上述分析都是针对时域峰值抵消信号的，其抵消噪声总功率在频域应分为带内和带外两部分，仅带内噪声用于计算SDR，而带外噪声将用于计算信道干扰。因此，利用抵消噪声总功率的噪声恢复与实际不符。该文将在文献[9]基础上继续推导抵消噪声的频域分布，并给出修正的噪声恢复模型。

2 峰值抵消噪声频域分布特性

2.1 抵消噪声的分布特性

类似于式(10)，首先建立抵消过程的频域非线性模型：

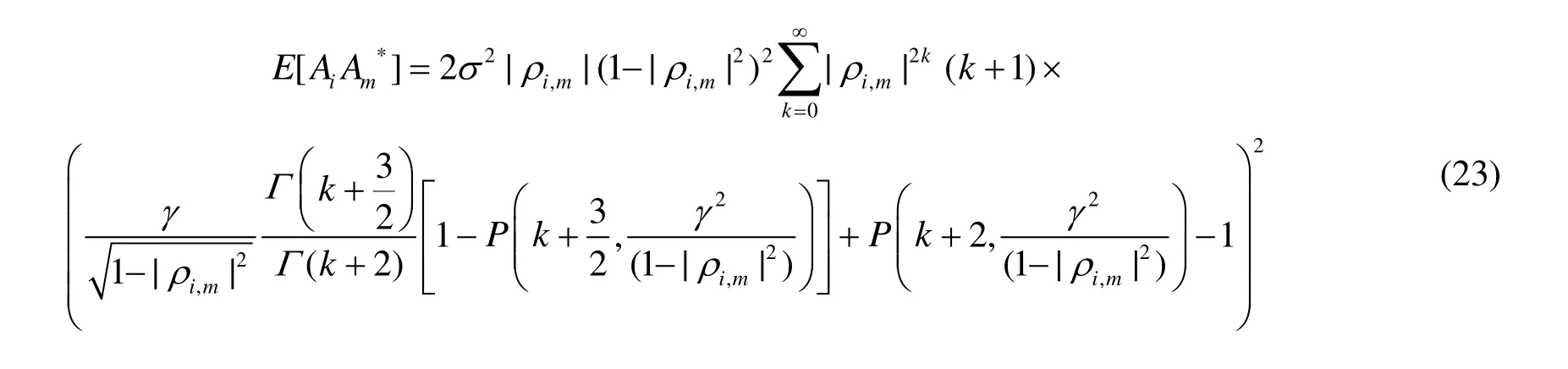
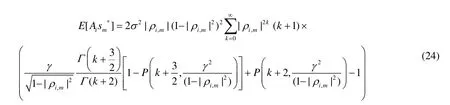
对于输入OFDM信号引入的非线性频域噪声峰值抵消，由过采样因子J、峰值抵消选择的功率门限 、窗函数波形gn及窗函数的宽度Nw共同确定。修正的信号噪声功率比为：

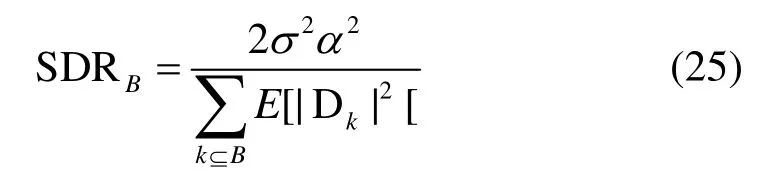
式中，B为传输数据子载波集合。

2.2 抵消噪声估计辅助的收端模型

对峰均比要求很高的OFDM系统，随着门限的降低，收端的峰值抵消操作对信号的峰值抵消程度将加大，从而对接收性能的影响也将加重。根据上述基于峰值抵消的OFDM信号模型，本小节给出一种接收端噪声恢复模型来消除峰值抵消失真对BER性能的影响。如图1b所示，接收信号经过时-频变换及滤波后，经过重新调制得到初始估计值。由于抵消噪声引起发送功率损失，此时的更新信噪比(signal to noise ratio, SNR)为：

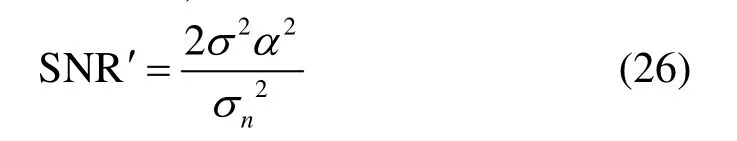
式中，2ns为信道噪声功率。除此之外，接收信号中除了信道噪声还包括峰值抵消引起的带内噪声，因此在初次解码过程中使用修正的接收信号的信号失真噪声比(signal to distortion plus noise ratio, SDNR)代替信噪比，即：

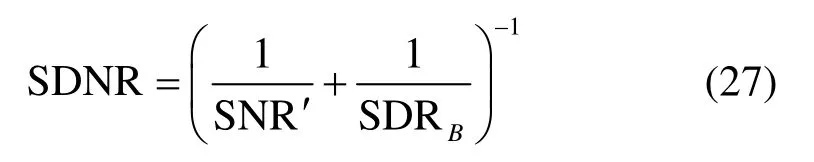
3 仿真结果

本文采用OFDM数据(16 QAM调制)，系统子载波数N=512，过采样因子J=4，即时域采样点及最大窗长为2 048，峰值抵消预设门限为3 dB和5 dB。系统采用(19,69)Turbo编码，发送功率归一化为1。

不同门限及不同截断长度下峰值抵消噪声分布仿真如图2和图3所示。图2中截断长度为1 024，图3的峰值抵消门限为5 dB。可以看出：理论曲线与仿真曲线完全重合，证明前面推导的抵消噪声功率式(27)与实际信号分布相符；增大门限和缩短截断窗长都将引起抵消噪声升高。比较图2和图3可知，峰值抵消噪声引起的带内抵消噪声主要由抵消门限决定(门限越低噪声越大)，而带外噪声则受截断长度影响更大。如图2所示，在1倍等效带宽处，3 dB门限下非线性过程引入的抵消噪声较5 dB门限高9 dB，而在2倍等效带宽处，两者的功率差降低到3 dB。而在相同抵消门限下，如图3所示，不同截断窗长的带内噪声水平几乎一样，而在2倍等效带宽处，两者的功率差约8 dB。

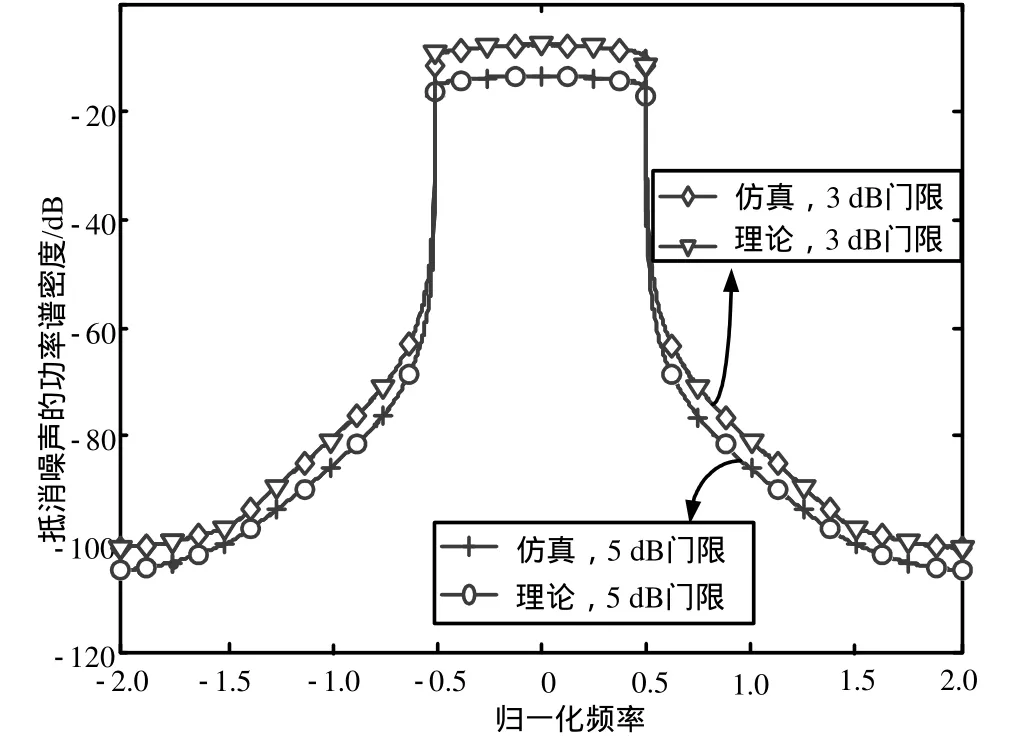
图2 不同门限下峰值抵消噪声分布仿真

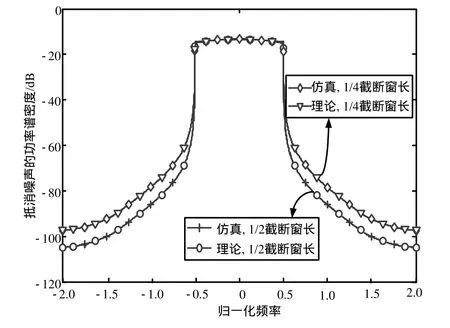
图3 不同截断长度下峰值抵消噪声分布仿真

图4给出了基于高斯窗函数的峰值抵消噪声分布仿真。其中抵消门限为5 dB，时域截断窗长为2 048(即最大窗长)。可以看出，基于高斯窗的抵消噪声分布与其方差取值有巨大关系。如2倍等效带宽处，使用方差为0.04的窗函数抵消噪声较方差为0.01时高约16 dB。但值得注意的是，此时的带内噪声较Sinc窗函数低。当系统对带外信道噪声要求较低时(如60 dB)，高斯窗函数将是一个较好的选择。

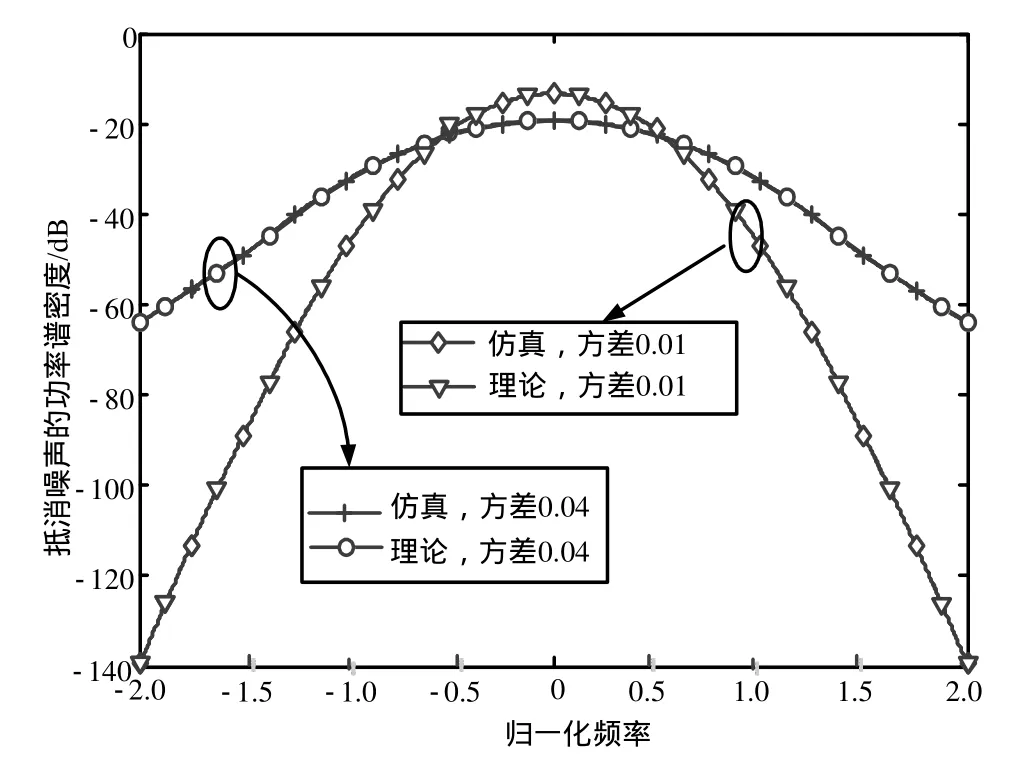
图4 基于高斯窗函数的峰值抵消噪声分布仿真

图5给出了不同抵消噪声估计的收端BER性能仿真，抵消门限为3dB，抵消函数选择截断窗长为1024的Sinc窗函数。可以看出，由于非线性抵消噪声，峰值抵消过程将降低信号的BER性能。采用公式(27)的抵消噪声的收端性能将优于采用公式(13)的传统抵消噪声估计方法。并且，随着迭代次数增加，其优势趋于明显。

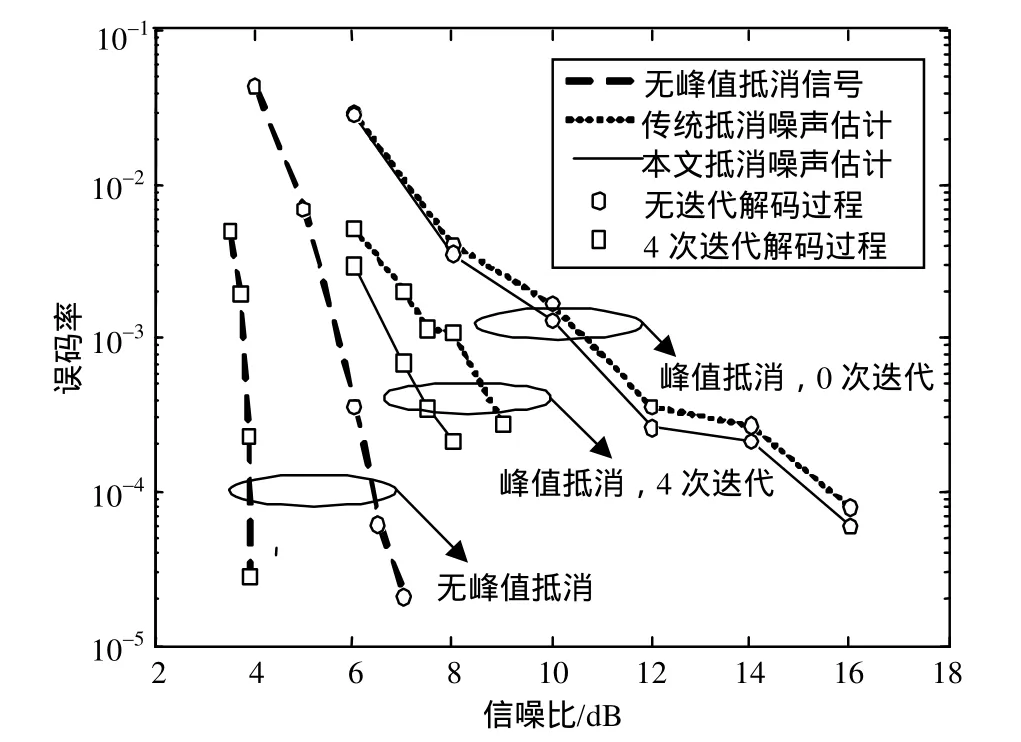
图5 不同抵消噪声估计的收端BER性能仿真

4 结 论

针对峰值抵消的OFDM系统，本文推导了峰值抵消噪声的频域分布特性，并通过数值仿真验证分析了抵消窗函数选择及截断长度对带外泄露的影响，为系统的优化设计提供了依据。此外，本文还给出了基于带内抵消噪声估计的信号检测方法。数值仿真结果表明，与现有抵消噪声估计方法相比，基于本文推导的频谱噪声能更好的进行噪声恢复，提高接收端性能。

[1] SARI H, KARAM G, JEAMCLAUDE I. Transmission techniques for digital terrestrial TV broadcasting[J]. IEEE Communication Magazine, 1995, 33(2): 100-109.

[2] CHEN Guo-guang, ANSARI R, YAO Ying-wei. Improved peak w indow ing for PAPR reduction in OFDM[C]//IEEE Vehicular Technology Conference, Barcelona: IEEE, 2009.

[3] JIANG Tao, WU Yue. An overview: peak-to-average power ratio reduction techniques for OFDM signals[J]. IEEE Transaction on Broadcasting, 2008, 54(2): 257-268.

[4] MAY T, ROHLING H. Reducing the peak-to-average power ratio in OFDM radio transmission systems[C]//IEEE VTC’98, Ottawa: IEEE, 1998.

[5] DAN Li-lin, XIAO Yue, NI Wei, et al. Improved peak cancellation for PAPR reduction in OFDM systems[J].IEICE Transactions on Communications, 2010, E93-B(1):198-202.

[6] WANG Y, LUO Z. Optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J]. IEEE Transactions on Communications, 2011, 1(59): 33-37.

[7] CHEN Hang-jun, HAIMOVICH A. An iterative method to restore the performance of clipped and filtered OFDM signals[C]//IEEE International Conference on Communications (ICC), [S.l.], 2003.

[8] WANG Lu-qing, TELLAMBURA C. A simplified clipping and filtering technique for PAR reduction in OFDM systems[J]. IEEE Signal Processing Letter, 2005, 3(12):453-456.

[9] BAI Wen-lin, DAN Li-lin, XIAO Yue, et al. Attenuation factor analysis for OFDM signals w ith peak cancellation[C]//IEEE VTC 2009-Spring, Barcelona: IEEE, 2009.

[10] DAN Li-lin, LI Teng, XIAO Yue, et al. Performance of peak cancellation for PAPR reduction in OFDM system[C]//International conference on circuit communications and signal (ICCCAS), Fujian: IEEE, 2008.

[11] LANGGLAIS C, HADDAD S, LOUET Y, et al. Clipping noise m itigation w ith capacity approaching FEC codes for PAPR reduction of OFDM signals[C]//The 8th international workshop on multi-carrier systems and solutions, Herrsching: IEEE, 2011.

[12] 雷霞, 赵颖, 唐友喜, 等. OFDM系统中限幅非线性失真迭代对消法性能分析[J].电子与信息学报, 2006, 28(10):1866-1869.

LEI Xia, ZHAO Yin, TANG You-xi, et al. Analysis of the performance of iterative estimation and cancellation of clipping distortion in OFDM[J]. Journal of Electronics &Information Technology, 2006, 28(10): 1866-1869.

[13] PRICE R. A useful theorem for nonlinear devices having Gaussian inputs[J]. IRE Transaction on Information Theory,1958, 4(2): 69-72.

编 辑 叶 芳