基于历史数据的贮存可靠度评价和预测

高军，李小兵，张泽

（1.工业和信息化部电子第五研究所，广东广州510610；

2.广东省电子信息产品可靠性技术重点实验室，广东广州510610；3.广州市电子信息产品可靠性与环境工程重点实验室，广东广州510610）

基于历史数据的贮存可靠度评价和预测

高军1，李小兵2，张泽3

（1.工业和信息化部电子第五研究所，广东广州510610；

2.广东省电子信息产品可靠性技术重点实验室，广东广州510610；3.广州市电子信息产品可靠性与环境工程重点实验室，广东广州510610）

贮存可靠度对弹药装备具有非常重大的意义，而产品全寿命周期内的贮存失效数据多种多样。基于弹药装备的历史贮存信息，应用统计方法建立了贮存可靠度的评价和预测模型，并给出数据处理和模型优选的方法，实现了弹药装备贮存可靠度的评价和预测。

弹药装备；贮存；可靠度；预测

0 引言

弹药装备是典型的长期贮存、一次使用的装备，不仅要求其具有较高的工作可靠性，而且需具有较高的贮存可靠性。长期处于贮存状态的弹药装备，虽然所承受的环境应力远远小于其在工作状态时所承受的量值，但由于产品的贮存时间长，贮存过程对弹药装备的可靠性的影响不容忽视。只有弹药装备具备高的贮存可靠性，才能够可靠地执行作战任务。

贮存可靠性水平的高低用贮存可靠度进行衡量，常用的贮存可靠度评估方法主要分为两大类:工程试验方法和统计分析方法[1]。工程方法利用弹药在研制阶段所能获得的一切信息，给出贮存可靠度评估结论；统计方法一般采用加速贮存试验的方法[2]，得出弹药贮存失效数据的统计规律，得到弹药贮存可靠度评估结论。为了高效、准确地对贮存可靠度进行评估，统计方法和工程试验相结合的方法目前成为了研究热点。庄喜盈等[3]深入到部组件级，考虑到温度和湿度等因素，采用神经网络算法进行了建模；刘秀萍[4]依据TTT-plot法对加速贮存失效数据进行了分析，建立了寿命预测模型秀萍；王军生、童雨等提出了相应的寿命预测贮存可靠度的模型，并给出了评估方法[5-6]；陈迪、周百里等[7]考虑到定检的维修问题，提出了定检修复条件下导弹系统的贮存可靠度模型。

在弹药贮存工程的实际中，由于贮存数量的不断增加，难以对每个贮存样品进行实时的检测，难以获得准确的失效信息，而较多的是获得弹药的定检数据，这导致许多基于精确失效数据的评定方法难以开展。基于此，本文提出了一种基于弹药历史贮存数据的统计评估方法。从弹药的实际贮存数据形式出发，建立可能的寿命分布模型，应用优选方法选择最优模型，最终建立贮存可靠度预测模型，实现了对弹药装备贮存寿命的评价和预测。

1 总体思路

图1 弹药贮存可靠度评价及预测流程

贮存可靠度评价与预测是与弹药装备贮存生命全周期息息相关的一项工作，该工作的开展以贮存期间弹药的各种数据为支持，借助于相应的数学方法，建立评价及预测模型，实现对弹药贮存可靠度的评价及预测。弹药贮存可靠度评价及预测流程如图1所示。

1.1 贮存数据采集及收集

可靠性评价与预测以数据为基础，在做好初始准备工作后，则应进行对所需数据的收集和采集，制定相应的数据采集表格，按照表格详细地记录所需的数据，并保证数据来源的真实性和可靠性。针对不同批次投入贮存的产品，明确每个产品投入贮存的日历时间，详细地记录其评价期内的检测信息与产品的技术状态；记录贮存场所的温度、湿度和光照等应力值，并分析这些应力因素的变化趋势；明确产品的检测周期及检测方式等[8]。

1.2 可靠度的计算

利用收集得到的数据，可以计算产品在各个时间点的可靠度。针对现场收集数据的实际情况，采用如下方法进行可靠度的计算。

假设有n个时段，对应的时间区间为[t0，t1]，[t1，t2]，…，[tn-1，tn]。第i个区间上收集得到产品的危险数为Ni，故障数为Di，则产品在此区间上的不可靠度为:

可靠度为:

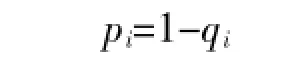
设产品在ti时刻的可靠概率pi为:

在获得定检数据的基础上，可以通过递推的方式算出产品在各个监测时刻的可靠度。

1.3 模型的建立

1.3.1 模型初选

常用的模型有指数分布、威布尔分布、对数正态分布等。

a）指数分布模型

指数分布是产品常用的寿命分布之一，它描述瞬时失效是常数的情况。指数分布常用来描述电子元器件的寿命分布，有许多独立元件组成的复杂系统的寿命分布，也常用指数分布来描述。

其概率密度函数为:式（1）中:λ——产品的失效率。

对于指数分布，除了简单的指数分布，带有位置参数的指数分布也是常用的寿命分布模型之一，即双参数指数分布，其分布函数如下:式（2）中:λ——产品的失效率。

b）威布尔分布模型

威布尔分布是可靠性研究中常用的一种比较复杂的分布，它是瑞典的威布尔在研究钢链的强度时提出的一种分布。这种分布起初多用来研究金属材料的疲劳寿命问题，后来广泛地应用于复杂机电产品的寿命分布模型。

其概率密度函数为:

式（3）中:α——尺度参数；

β——形状参数；

γ——位置参数。

c）对数正态分布模型

对数正态分布是其随机变量的自然对数呈正态分布的一种形式，也是系统常用寿命分布模型之一，尤其是在维修性分析领域被广泛地采用。

式（4）中:μ——对数均值；

σ——对数标准差。

1.3.2 参数评估

利用失效数据对模型中的未知参数进行评估。通常可用的参数估计方法有矩估计法和最小二乘法两种方法。以指数分布为例，说明最小二乘的评估方法。

指数分布的累积分布函数F（t）=1-exp（-λt）。

令，

对累积分布函数变形得y=λx，则有

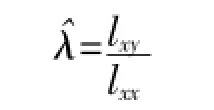
其中

1.3.3 模型检验与优选

对于各个模型评估得出的参数，需要检验数据符合模型的程度，检验拟合优度，选择最佳的模型。可以选择通用的Kolmogorov-Smimov（K-S）检验法。

K-S检验法的检验公式如下；

式（5）中:Fn（t）——采用估计方法得到的累积失效率，如中位秩法；

F0（t）——拟合选用的分布模型；

α——置信水平；

n——样本个数；

Dn，α——临界值，可以查表获得。

1.4 可靠度预测

根据求得的产品贮存可靠度模型，预测产品若干年后的贮存可靠度。

2 案例分析

某产品15年内定检得到的失效数据如表1所示。

表1 产品区间可靠度数据处理表

将各个时间点的可靠度绘制成曲线，其变化趋势如图2所示。

图2 可靠度变化趋势

根据图中产品可靠度的趋势，初步采用指数分布，双参数指数分布，威布尔分布和对数正态分布分别对其拟合。采用最小二乘法估计模型的参数，并采用K-S检验法，检验各个估计值符合寿命模型的程度，结果如表2所示。

表2 各个模型K-S检验结果表

计算结果表明，4种模型的K-S检验均通过，但双参数指数分布的检验量最小。因此，双参数指数分布为最优分布模型。假定预测该批弹药贮存到20年时的可靠性水平，即t=20，产品的可靠度R（t）=0.3 523。

3 结束语

本文利用弹药装备在贮存期间的真实定检数据，通过模型初选和优选，建立了贮存可靠度评价与预测模型。最后，以某产品的实际数据进行了分析，结果表明，该方法能够实现贮存可靠度的评价和预测。

[1]李海波，张正平，黄波，等.导弹贮存试验技术与贮存可靠性评估方法研究[J].质量与可靠性，2006（6）: 20-23.

[2]高军，阳川.性能退化数据的归一化处理[C]//中国电子学会可靠性分会第十四届学术年会论文集.2008.

[3]庄喜盈，孟建新.基于BP神经网络的空空导弹贮存可靠性预测模型研究[J].航空兵器，2008（6）:59-62.

[4]刘秀萍.电子产品的加速贮存可靠性模型及统计分析[D].贵州:贵州大学，2007.

[5]王军生，徐胜红，徐智明.导弹贮存可靠性预测建模方法[J].战术导弹技术，2007（6）:28-32.

[6]童雨，李晓钢.导弹贮存可靠性预测模型[J].装备环境工程，2005（5）:42-50.

[7]陈迪，周百里，费鹤良.导弹系统贮存可靠性预测的数学模型[J].宇航学报，1996，17（3）:51-57.

[8]李青，李宁萍.装备贮存可靠性数据的收集与分析方法[C]//中国系统工程学会第十届年会论文集.1998.

Storage Reliability Assessment and Prediction Based on
History Data

GAO Jun1，LI Xiao-bing2，ZHANG Ze3
（1.CEPREI，Guangzhou 510610，China；
2.Guangdong Key Laboratory of Electronics and Information Technology Product Reliability，
Guangzhou 510610，China；
3.Guangzhou Key Laboratory of Reliability and Environmental Engineering of Electronic Information
Product，Guangzhou 510610，China）

Storage reliability is of great significance to the ammunition equipment，and storage failure data in the whole product life cycle is varied.Based on the history storage data of the ammunition equipment，the storage reliability evaluation and prediction model isestablishedusing the statistics.The method for data analysis and selection of the optimal model is presentedtorealize the assessment and prediction of the storage reliability of a ammunition equipment.

ammunition；storage；reliability；prediction

TB 114.3

：A

：1672-5468（2014）04-0008-04

10.3969/j.issn.1672-5468.2014.04.003

2014-02-19

2014-05-09

高军(1978-)，男，湖南长沙人，工业和信息化部电子第五研究所可靠性与环境工程研究中心高级工程师，在读博士研究生，主要从事质量与可靠性研究工作。