Leader-follower Consensus of Upper-triangular Nonlinear Multi-agent Systems
2014-02-07ChenghuiZhangLeChangXianfuZhang
Chenghui Zhang Le Chang Xianfu Zhang
There are many unsolved problems in the research area of multi-agent systems.One difficult problem is that the structures of many multi-agent systems,especially some nonlinear multi-agent systems,are too complex to deal with.A lot of literature has studied this problem,for example,[2,3,10]studied the linear systems,[5,8,9,11]dealt with the second-order agent systems,[4]presented necessary and sufficient conditions for the consensus of multi-agent systems described by Vicsek′s model.Another difficult problem is that the multi-agent systems greatly differ from each other in the communication topologies.Reference[1]studied the problem that the information received by each agent is corrupted by measurement noises.References[11,12]addressed consensus problems when the information is with or without communication delay.Reference[13]worked on the consensus behavior of multi-agent systems under digital network topology.The consensus problem with input constraints was considered in[14].
A critical problem for coordinated control is the consensus problem,which is to design appropriate protocols and
I.INTRODUCTION
IN recent years,there has been an increasing research
interest in the coordinated control problems of the multi-agent systems[1-11],which have wide applications in many algorithms such that the group of agents can reach a consensus on the shared information in the presence of limited and unreliable information exchange.Recently,the consensus problem has been studied for multi-agent systems in a general form.Reference[2]studied the consensus problem for multi-agent linear dynamic systems.Reference[6]designed the globalH∞consensus algorithms for a class of multi-agent nonlinear systems with Lipschitz non-linearity and directed communication graphs.
Due to the existence of abundant nonlinear physical systems in practical and the need of precise simulation to describe many commonly observed phenomena,the study of nonlinear multi-agent systems is getting more and more important.Because of complexity of nonlinearity,there is no control procedure which can be applied to all nonlinear multi-agent systems.But there are several effective ways to design controllers for some nonlinear systems that can be transformed into specific nonlinear forms.The lower-triangular nonlinear multi-agent systems have been studied in[7,15,16],but to our best knowledge,there is no literature which has handled the upper-triangular nonlinear multi-agent systems.
In our work,the leader-follower consensus problem is studied for the upper-triangular nonlinear multi-agent systems with fixed(time-invariant)communication topologies.The consensus protocols of both the local state and observer-based dynamic output are considered.Compared to the lower-triangular systems studied in[7,15,16],the consensus problem of the upper-triangular nonlinear systems is harder,as the input appears in every nonlinear term.
Inspired by[17-20],we introduce a rescaling transformation and have a new design freedom to stabilize the errors between the leader signals and follower signals.When the full state is not available,observers can be designed such that their signals asymptotically approach the signals of agents.As a result,using the observer-based compensation,dynamic output consensus protocol can be constructed.An example is given to illustrate the proposed consensus algorithms at the end of this paper.
Throughout this work,‖·‖denotes the Euclidean norm for a vector,or the induced Euclidean norm for a matrix.
II.GRAPH THEORY AND PROBLEM STATEMENT
A.Graph Theory
In this section,we present some definitions,notations and lemmas in graph theory,which will be used in our paper.A simple graph is an undirected graph if it has no self-loops and no more than one edge between any two different nodes.The simple graph denoted byG(V,ℑ,A)consists of anNnode setV,an edge setℑand a weighted adjacency matrixA=[aij]∈RN×N.We denote the nodes inVas{s1,s2,···,sN}.
The edge of the graphG,eij=(si,sj),belongs toℑ.The graph is undirected,i.e.,onceeij∈ℑ,theneji∈ℑ.As the graph is a simple graph,the adjacency matrix is defined asaii=0 andaij=aji≥0(i/=j),whereaij>0 if and only ifeij∈ℑ.A path inGbetweens1andsjis a sequence of edges of the form(s1,sk),k=1,2,···,j.The graphGis said to be connected if there exists a path between any two nodes ofG.The neighbor set of nodesiis defined asNi={sj∈V:eij∈ℑ}.The degree ofGis a diagonal matrixD=diag{d1,···,dN},wheredi=Psj∈Niaijfori=1,2,···,N.The Laplacian matrix of graphGis defined asL=D-A.It is apparent that the Laplacian matrixLis symmetric.His a subgraph ofG,i.e.,any two nodes ofHare adjacent inHonly if they are adjacent inG.SubgraphHofGis called component ofGif it is a maximal connected subgraph.
We considerNmodes inVasNagents,whose relationship can be described by the simple and undirected graphG.(si,sj)is an edge ofGif and only if agentiandjare neighbors.Moreover,we have another graph˜Gwhose node set is{s0}∪V.Gis the subgraph of˜G,ands0is considered as the leader.The edgee0j=(s0,sj)exists if and only if agentjconnects to the leader(j=1,2,···,N).The degree matrix of˜Gis denoted byB=diag{b1,···,bN},wherebi≥0 is the adjacency weight between agentiand the leader.bi=0 means that agentidoes not connect to the leader.˜Gis connected if at least one agent in each component ofGis connected with the leader.We defineˆL=L+B,and have the following useful lemma aboutˆL.
Lemma 1[5,7].If graph˜Gis connected,then the symmetric matrixˆLassociated with˜Gis positive definite.
B.Problem Statement
In this paper,we deal with a group ofN+1 agents with identical upper-triangular nonlinear dynamics,where the agent indexed by 0 is referred as the leader and the other agents indexed by 1,2,···,Nare called followers.The communication topology of theN+1 agents is denoted by˜G,while the topology of theNfollowers is denoted byG.For the agents,we have the following assumptions.
Assumption 1.All follower agents know the input of the leader,and the information between the leader and any follower agent is unidirectional,i.e.,the leader receives no information from any follower agent.
Assumption 2.The communication topology of theN+1 agents is connected,i.e.,the graph˜Gis connected.
For agentk(k=0,1,···,N),the system has the following form

wherexk,i∈R(i=1,2,···,n),yk∈Randuk∈Rrepresent the state,output,and input of thekth agent,respectively,and nonlinear functionfi(i=1,2,···,n-1)represents the nonlinear effect within thekth agent,and satisfy the following growth assumption.
Assumption3.Forp,q= 0,1,···,N,and any(t,xp,i+2,···,xp,n,up),(t,xq,i+2,···,xq,n,uq)∈Rn-i+1(i=1,2,···,n-1),there exists a constantc>0,such that

wherexp,n+1=xq,n+1=0.
Remark 1.Reference[7]considered the leader-follower consensus problem of a class of multi-agent systems in the lower-triangular form.Hence,the problem considered here can be viewed as the counterpart of that in[7].In our work,the input of thekth agent can be allowed to be included in all nonlinear terms of thekth agent,which makes our design procedure more complicated,compared with[7].
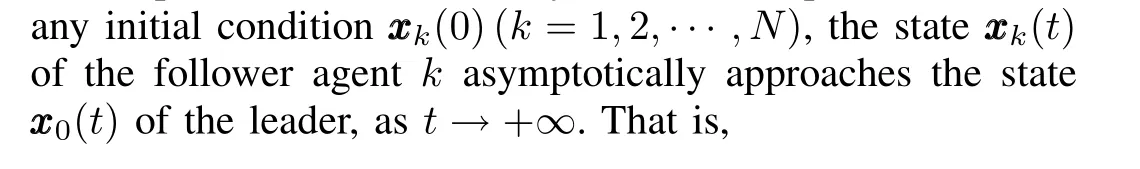

Definition 1[7].The leader-follower consensus problem of the nonlinear multi-agent system(1)can be solved by consensus protocoluk,if and only if under the protocoluk,for

Our objective is to design consensus protocols by both the state and output feedback,which solve the leader-follower consensus problem of the nonlinear multi-agent system(1).
As defined above,˜GandGare the communication topologies of theN+1 agents and theNfollower agents,respectively.We use matrixLandBto denote the Laplacian matrix ofGand the degree matrix of˜G,respectively.We getˆLby ˆL=L+B.According to Lemma 1,ˆLis positive definite.We have the following useful lemma aboutˆL.
Lemma 2[7].IfˆLis positive definite,then there exists a row vectorKsuch that the matrixIN⊗A+ˆL⊗BKis Hurwitz.Furthermore,there exists a positive definite matrixPsatisfying

III.MAIN RESULTS
A.State Feedback Control
Our main result of the state feedback control problem with the full states known,can be summarized as the following theorem.
Theorem 1.Under Assumptions 1~3,the leader-follower consensus problem of the nonlinear multi-agent system(1)can be solved by the consensus protocol of the following form,fork=1,2,···,N,
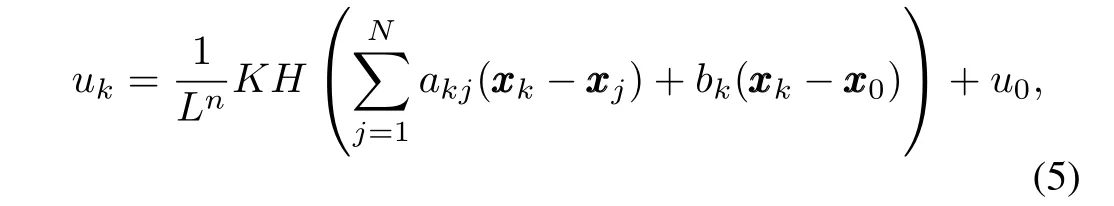
whereKis a row vector given in Lemma 2,and diagonal matrixH=diag{1,L,···,Ln-1},withL≥1 being a constant large enough.
Proof.For the consensus problem,we need to consider the state errors between the leader and followers.
Fork=1,2,···,N,letek,i=xk,i-x0,i(i=1,2,···,n),we have
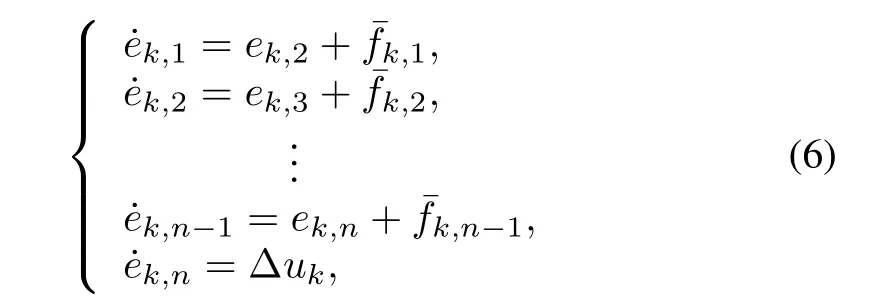
whereΔuk=uk-u0,and¯fk,i=fi(t,xk,i+2,···,xk,n,uk)-fi(t,x0,i+2,···,x0,n,u0),i=1,2,···,n-1.
The consensus error dynamics(6)can be rewritten as
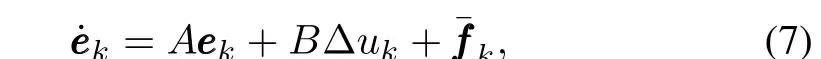
Introducing a transformation of coordinates
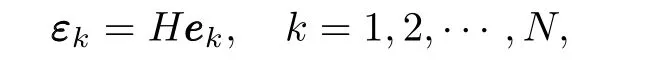
whereH=diag{1,L,···,Ln-1},withL≥1 being a constant to be determined later,system(7)can be converted into
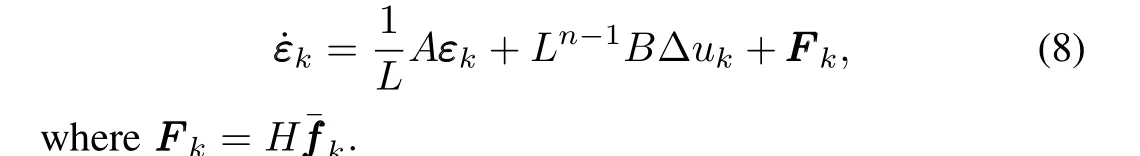
Denotingε=[εT1,εT2,···,εTN]T,and using(5),the consensus error dynamics(8)can be further rewritten in the compact form of

LetV=εTPε,wherePis given in Lemma 2.Th
e derivative ofValong system(9)is given as


Noticing the definition of Δukin(5)and(6),we can get the following derivation

whereAkis defined asAk=αk⊗In,withαkbeing thekth row of matrixˆL.
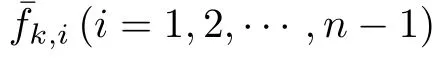


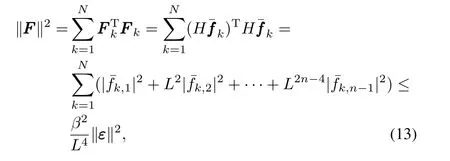
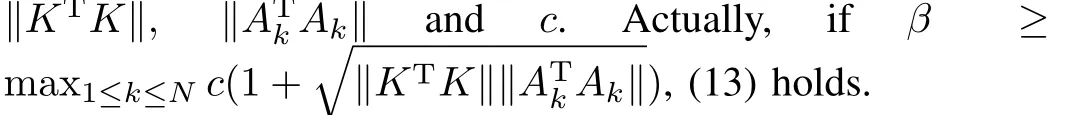
With(13)and(10),we have
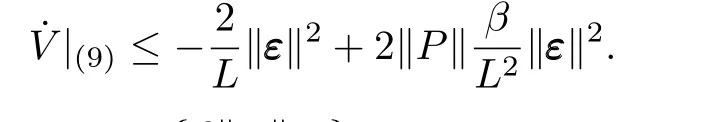
ChoosingL≥max{β‖P‖,1}+α,whereαis any positive constant,we get


Remark 2.BothKTKandATkAkare positive definite matrices,so their norms can be replaced by the maximum of their eigenvalues.
Remark 3.From the definitionAk=αk⊗Inin(11),one can calculate that

Since det(λIN-αTkαk)=λN-1|λ-αkαTk|,all eigenvalues ofATkAkequal 0 orαkαTk.It is easy to get the maximal eigenvalue ofATkAk.
Remark 4.It can be seen that the study of upper-triangular multi-agent systems is more difficult than that of lower-triangular multi-agent systems,as the input is allowed to appear in each nonlinear term of the upper-triangular multi-agent systems.To our best knowledge,there is no literature dealing with the upper-triangular multi-agent systems.Compared with the technologies used to study the lower-triangular multi-agent systems in[7,15,16],the algorithm in our paper is novel and easy to design.
B.Output Feedback Control
In this section,the output feedback protocol problem is considered when the full state is not available.
First,we construct the observers for all agents and the inputs for the follower agents.
Following the ideas of[17-20],the observer of every agent has the following form,fork=0,1,···,N,

whereL≥1 will be determined later,andci≥0(i=1,2,···,n)are coefficients of a Hurwitz polynomial

The input of agentkhas the form of


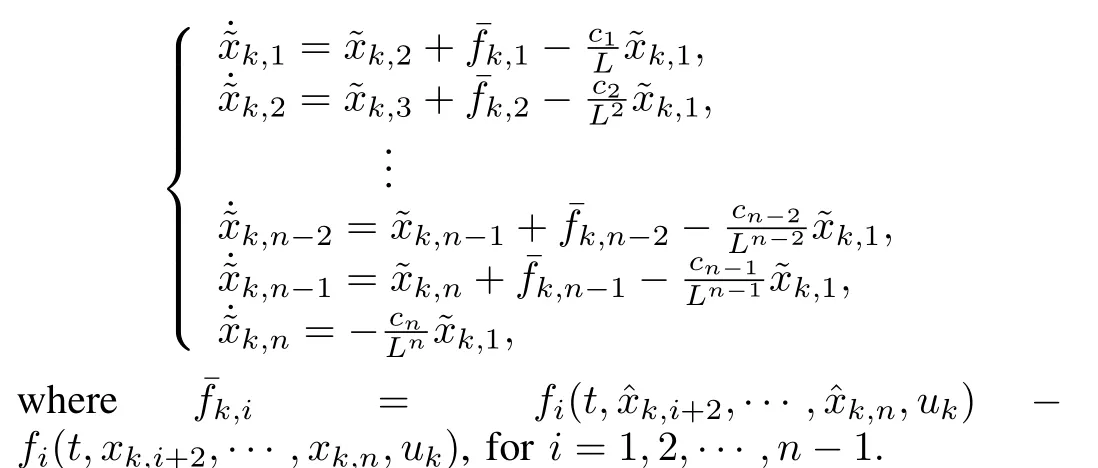




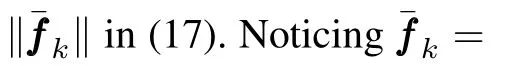
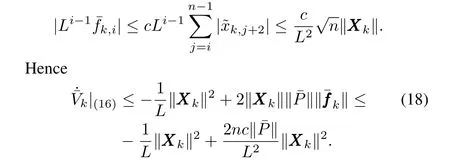


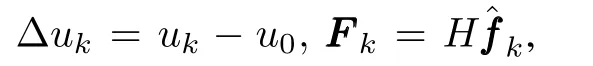
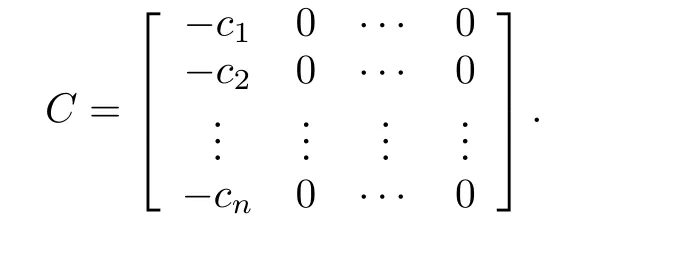
Introducing(15)into(19),we get


From Lemma 2,one knows that there exists a positive definite matrixPsuch that(4)holds.
We consider the Lyapunov functionV1=εTPε ,whose derivative along system(21)is
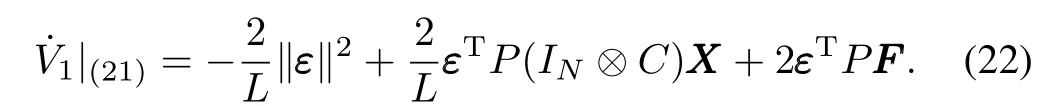

From the definition of Δukin(15)and(19),we can get
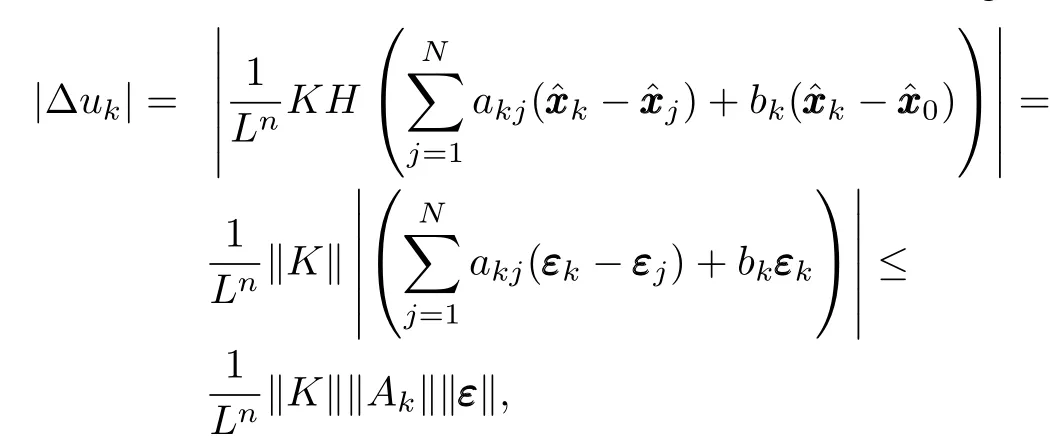


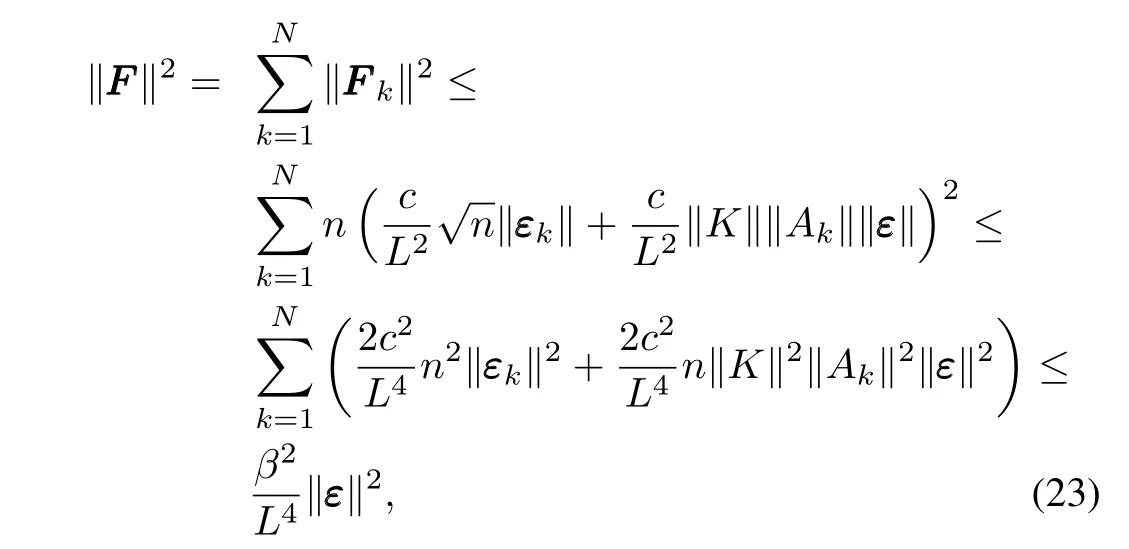
whereβis dependent on the known constants‖Ak‖,‖K‖,c,nandN.
From(22)and(23),one obtains

Theorem 2.Under Assumptions 1~3,the consensus problem of the multi-agent system(1)can be solved by the dynamic output consensus protocol of the form(14)and(15).
Proof.We choose the Lyapunov function as
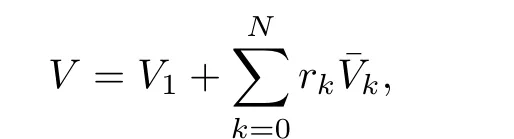
With(18)and(24),the derivative ofVhas the following calculation

then,we can get
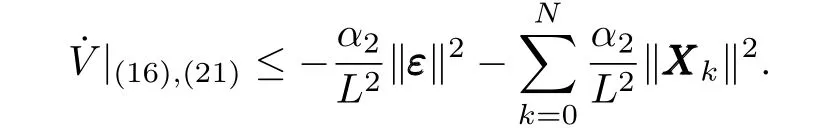
Noticing the fact thatLsatisfiesL≥max{2nc‖¯P‖,1}+α2,and using(22),one can get

Remark 5.It is obvious that the observer of every agent used in our paper can only use the output signal of its own agent.This is much simpler and more efficient to design the observers for multi-agent system.
IV.ANUMERICAL EXAMPLE
To illustrate the designed protocols,the following numerical example is presented.
We consider a group of 3+1 agents with the identical nonlinear dynamics,which are indexed by 0,1,2,3.In this multi-agent system,the agent indexed by 0 is referred as the leader,and the agents indexed by 1,2,3 are called followers.We also assume that all the follower agents know the input of the leader.Fork=0,1,2,3,agentkis described by

The communication topology graph is shown in Fig.1.

Fig.1.Communication topology.
The adjacency matrix and degree matrix of the follower agents are denoted byAandB,respectively.From Fig.1,AandBcan be defined as follows

It is easy to verify that Assumptions 1~3 hold for this multi-agent system,andc=0.2.
First,the state feedback consensus protocol provided in Section III-A has the form of
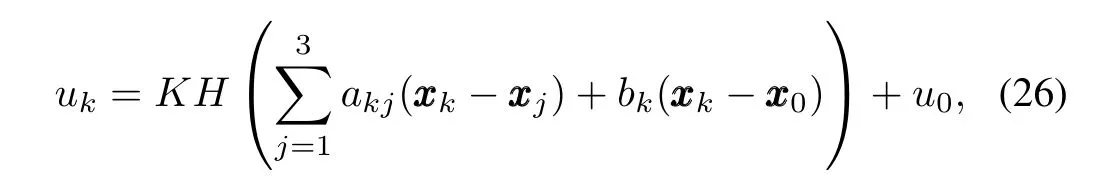
Fig.2 shows the state responses of the closed-loop system consisting of(25)and(26),with the initial condition that

andu0(t)=0.
It can be seen that the signals of all follower agents do asymptotically tend to the states of the leader in Fig.3,which shows the convergence of errors between the signals of the leader and followers.
Second,we consider the output feedback consensus problem.Using the method in Section III-B,the observer for agentk(k=0,1,2,3)can be designed as


Fig.2.The state responses of the closed-loop system with state consensus protocol.
Then,fork=1,2,3,the inputukof each follower agent has the following form
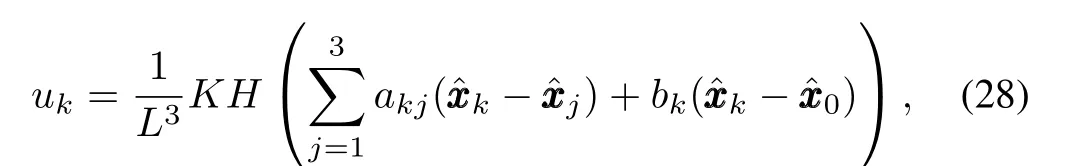

We also set the initial condition as before and the initial observer signals to be zero.Figs.4 and 5 show the states,the errors of the signals between the leader and followers of the closed-loop system consisting of(25),(27)and(28),respectively.
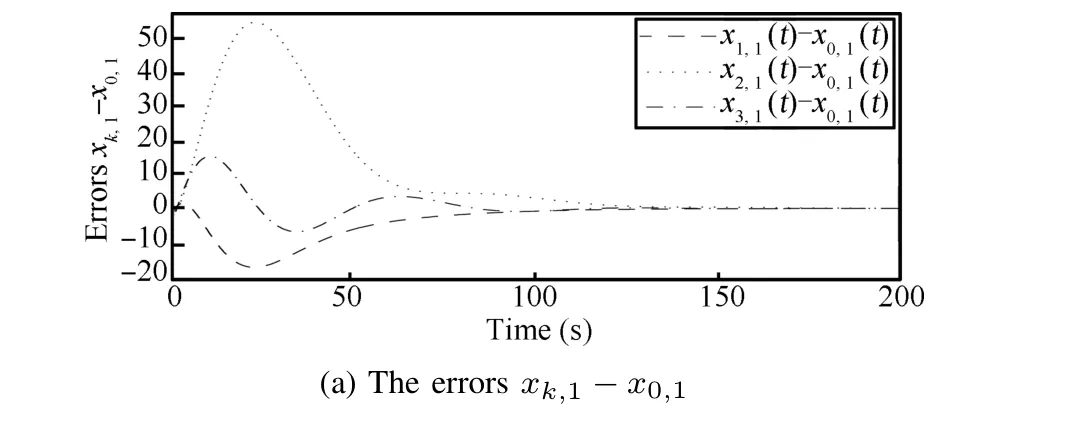
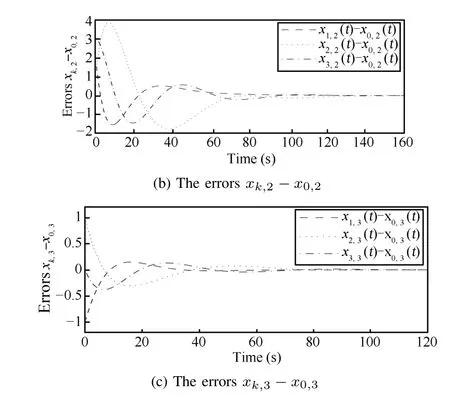
Fig.3. The error responses of the closed-loop system with state consensus protocol.

Fig.4. The states responses of the closed-loop system with output consensus protocol.
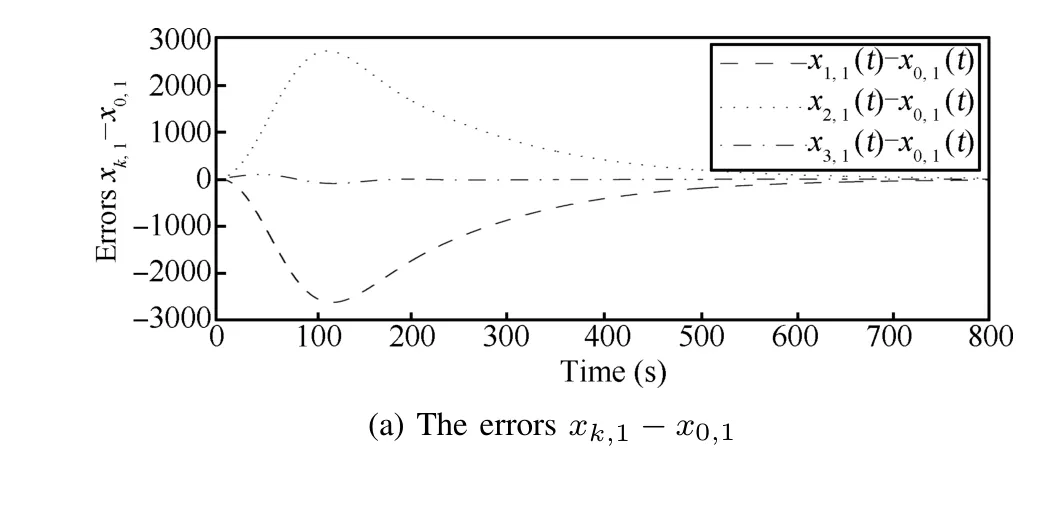

Fig.5.The error responses of the closed-loop system with output consensus protocol.
V.CONCLUSIONS
In this paper,we study the leader-follower consensus problem for a class of nonlinear multi-agent systems.Each agent has the identical nonlinear form and is coupled with an undirected communication topology.Different from[7],in our work,the input of thekth agent can be included in all nonlinear terms of thekth agent.Under the condition of undirected communication,we construct two consensus protocols,full state and dynamic output consensus protocol,for a class of nonlinear multi-agent systems.
[1]Ma C Q,Li T,Zhang J F.Consensus control for leader-following multi-agent systems with measurement noises.Journal of Systems Science and Complexity,2010,23(1):35-49
[2]Seo J H,Shim H,Back J.Consensus of high-order linear systems using dynamic output feedback compensator:low gain approach.Automatica,2009,45(11):2659-2664
[3]Wang J H,Cheng D Z,Hu X M.Consensus of multi-agent linear dynamic systems.Asian Journal of Control,2008,10(2):144-155
[4]Li Q,Jiang Z P.Global analysis of multi-agent systems based on Vicsek′s model.IEEE Transactions on Automatic Control,2009,54(12):2876-2881
[5]Hong Y Q,Hu J P,Gao L X.Tracking control for multi-agent consensus with an active leader and variable topology.Automatica,2006,42(7):1177-1182
[6]Li Z,Liu X,Fu M,Xie L.GlobalH∞consensus of multi-agent systems with Lipschitz non-linear dynamics.IET Control Theory&Applications,2012,6(13):2041-2048
[7]Wang X H,Ji H B.Leader-follower consensus for a class of nonlinear multi-agent systems.International Journal of Control,Automation and Systems,2012,10(1):27-35
[8]Zhu W,Cheng D Z.Leader-following consensus of second-order agents with multiple time-varying delays.Automatica,2010,46(12):1994-1999
[9]Li W X,Chen Z Q.Leader-following consensus of second-order multi-agent systems with time-delay and nonlinear dynamics.In:Proceedings of the 31st Chinese Control Conference.Hefei,China:IEEE,2012.6124-6128
[10]Ma C Q,Zhang J F.Necessary and sufficient conditions for consensus-ability of linear multi-agent systems.IEEE Transactions on Automatic Control,2010,55(5):1263-1268
[11]Qin J H,Gao H J,Zheng W X.Second-order consensus for multi-agent systems with switching topology and communication delay.Systems&Control Letters,2011,60(6):390-397
[12]Huang Q Z.Consensus analysis of multi-agent discrete-time systems.Acta Automatica Sinica,2012,38(7):1127-1133
[13]Yu H W,Zheng Y F,Li D G.Consensus behavior of multi-agent systems under digital network topology.Acta Automatica Sinica,2012,38(3):357-363
[14]Yan J,Guan X P,Luo X Y,Yang X.Consensus and trajectory planning with input constraints for multi-agent systems.Acta Automatica Sinica,2012,38(7):1074-1082
[15]Wang Z,Zhang W L,Guo Y.Adaptive output consensus tracking of uncertain multi-agent systems.In:Proceedings of American Control Conference.San Francisco,CA,USA:IEEE,2011.3387-3392
[16]Yoo S J.Distributed adaptive containment control of uncertain nonlinear multi-agent systems in strict-feedback form.Automatica,2013,49(7):2145-2153
[17]Zhang X F,Boukas E K,Liu Y G,Baron L.Asymptotic stabilization of high-order feed forward systems with delays in the input.International Journal of Robust and Nonlinear Control,2010,20(12):1395-1406
[18]Zhang X F,Baron L,Liu Q R,Boukas E.Design of stabilizing controllers with a dynamic gain for feed forward nonlinear time-delay systems.IEEE Transactions on Automatic Control,2011,56(3):692-697
[19]Zhang X F,Liu Q R,Baron L,Boukas E.Feedback stabilization for high order feed forward nonlinear time-delay systems.Automatica,2011,47(5):962-967
[20]Zhang X,Gao H,Zhang C.Global asymptotic stabilization of feed forward nonlinear systems with a delay in the input.International Journal of Systems Science,2006,37(3):141-148
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Modeling and Hybrid Optimization of Batching Planning System for steel making-continuous Casting Process
- Timesharing-tracking Framework for Decentralized Reinforcement Learning in Fully Cooperative Multi-agent System
- Containment Control of General Linear Multi-agent Systems with Multiple Dynamic Leaders:a Fast Sliding Mode Based Approach
- Bilateral Teleoperation of Multiple Agents with Formation Control
- Distributed Sparse Signal Estimation in Sensor Networks UsingH∞HH-Consensus Filtering
- Adaptive Nonsingular Terminal Sliding Mode Control Design for Near Space Hypersonic Vehicles
