Bilateral Teleoperation of Multiple Agents with Formation Control

Jing Yan Xian Yang Cailian Chen Xiaoyuan Luo Xinping Guan

With the introduction of communication network into tele-operation system,time delays are unavoidable when data information is back and forth between the master robot and

I.INTRODUCTION

BILATERAL teleoperation system has become an active area of research and attracted multi-disciplinary researchers including scientists in system control theory,statistical physicists,biologists,clinicians,etc.A bilateral teleoper-ator is typically composed of five interconnected elements:the human operator,the master robot,the communication network,the slave agent(e.g.,unmanned ground vehicle,unmanned aerial vehicle and unmanned underwater vehicle)and the slave agent.These time delays can affect the whole stability of the system,and therefore many researchers have considered their influence.Based on passivity and input to state stable(ISS)theories,the stability analysis and controller design problems were extensively studied in[4-6].The symmetric and constant time delays were investigated,and an effective stability criteria was presented in[7].Recently,the stability analysis problem with asymmetric and time-varying delays was considered in[8-10].However,these research efforts were well framed under the assumption that the configuration of teleoperation system was single-master-single-slave.Because of the increasing complexity of tasks,“multi-agent systems”[11,12]should be applied to the teleoperation system,i.e.,multiple slave agents are required in the future developments of teleoperation systems.Compared with single-mastersingle-slave system,teleoperation of multiple slave agents can complete multiple tasks in a shorter time,cover larger-scaled areas,and adapt more easily to single point failure.With these abilities,formation of a single-master-multi-slave teleoperation system provides the capacity of cooperatively performing challenging tasks in a team,such as search and rescue,reconnaissance,surveillance and earth magnetic field study.Due to the complexity of modelling and coupling,there are few research efforts on the single-master-multi-slave teleoperation systems.More recently,a multi-slave teleoperation system based on bearing only measurements was developed in[13].In[14],bilateral teleoperation of a formation of car-like planetary rovers under communication delays was addressed.Yet,the detailed stability conditions were not given in these papers.Moreover,[15]designed a passifying proportional-derivative controller and gave the stability conditions.However,the time delays were constant and the gravitational force was omitted in the dynamics formulation.To the best of our knowledge,cooperation control of multi-slave teleoperation system with time-varying delays has been received less attention.

On the other hand,most of the results mentioned above assume that all data transmissions can be performed with infinite precision,but the effect of the data quantization is ignored.Due to the limited transmission capacity of the network and some devices in the closed-loop systems(such as A/D and D/A converters),data transmitted in a practical teleoperation system should be quantized before being sent to the next network node.In the existing literature,to the best of our knowledge,there is yet no serious effort to investigate the quantization problem while considering the multi-slave teleoperation system with variable time delays.

This paper attempts to overcome these limitations by applying “multi-agent systems”to the teleoperation system.Additionally,the configuration of networked teleoperation system is extended to single-master-multi-slave.Then,a novel master-slave formation protocol is proposed for single-master-multi-slave teleoperation system with time-varying delays and quantization.The performance goals are to ensure boundedness of the state tracking error between the master robot and slave agents when slave agents are in hard contact with the environment,and to achieve the formation when slave agents are allowed to move freely.Finally,the sufficient conditions for stability are also given,and the closed-loop multi-slave bilateral teleoperation system is proved to be convergent.By operating the master robot,humans can control the overall behavior of slave agents while perceiving combined environmental forces on them.The main contributions of this paper are twofold.

1)Compared with the previous work,both quantization and time-varying delays are considered.Then,a dynamic quantization measurement is proposed to quantize the output signals.

2)Multi-agent systems are applied to the slave site,then a teleoperation system is considered.Correspondingly,a novel master-slave formation protocol is proposed for master robot and slave agents.

Notation.Rndenotes then-dimensional Euclidean space,Rn×nis the set ofn×nreal matrices,Iis the identity matrix of appropriate dimension,‖·‖stands for the theL2norm,and|·|for the Euclidean norm.The notationX＞0(orX≥0),forX∈Rn×n,means that matrixXis a real symmetric positive definite(or positive semi-definite).

II.PROBLEM FORMULATION

Consider the task of remotely controlling a formation ofN n-degree-of-freedom(DOF)slave agents coupled bilaterally throughNvariable time delayed communication channels to a singlen-DOF master robot.Their corresponding non-linear Lagrangian dynamics is described by

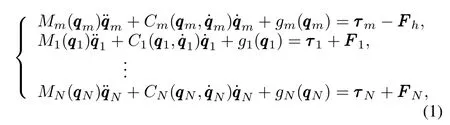
The above model has some important properties[16].

Property 1.The inertia matrix is lower and upper bounded,i.e.,

whereλminandλmaxare the minimum and maximum eigenvalues of matrixMi(qqqi),respectively.

Property 2.The Coriolis and inertia matrices are related as

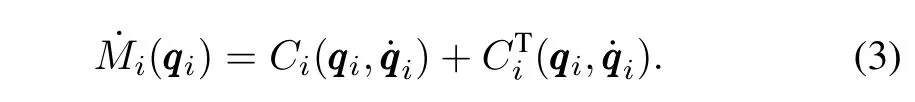
Property 4.For allqqqi, xxx, yyy∈Rn,there exists a positive scalarςisuch that‖Ci(qqqi, xxx)yyy‖≤ςi‖ xxx‖‖ yyy‖.

For stability analysis,the following lemmas and assumptions are used.

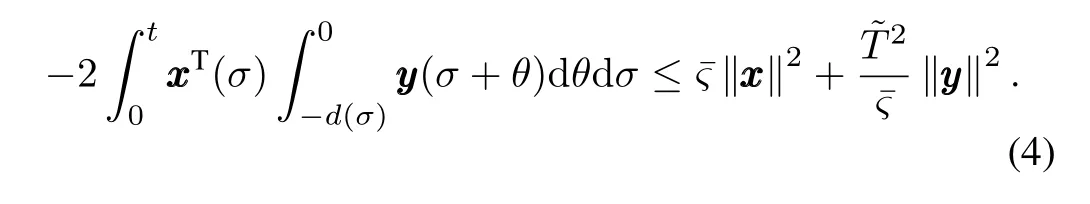
Assumption 1.The human operator and the environment are passive wherei=1,···,N,i.e.,

Measurement and control signals are required to be quantized before transmission.The quantization strategies,which convert a real-valued signal into a piecewise constant one taken from a finite set of values,are generally categorized into static and dynamic ones.The static strategy[17]presumes that data quantization at timekis only dependent on the data at timek.The attraction of static quantizer is simplicity of its coding/decoding schemes.But it requires an infinite number of quantization bits to ensure asymptomatic stability.To relax this restriction,dynamic quantization strategy may be a good choice[18-20].It has the advantage to scale the quantization levels dynamically in order to increase the region of attraction and to attenuate the steady state limit cycle.In some literature,most employed dynamic quantizers use dynamic scaling in conjunction with a static quantizer.

Letzzz∈Rnbe a variable to be quantized.Quantizerf(·)is de fined as a piecewise constant functionf:Rn→Q,whereQis a finite subset ofRn.This leads to a partition ofRninto a finite number of quantization regions in the form of{ zzz∈Rn:f(zzz)=ϑ}, ϑ ∈Q.Whenzzzdoes not belong to the union of a finite number of quantization regions,the quantizer saturates.More precisely,it is assumed that there exist positive real numbersHand Δ such that the following two conditions hold:

The first condition gives a bound of the quantization error when the quantizer does not saturate,and the second condition provides a way to detect the possibility of saturation.Hand Δ are considered as the quantization range and error off(·),respectively.

1In order to keep equations as clear as possible,the argument of all time-dependent signals will be omitted(e.g.,qqq˙≡ qqq˙(t)),except for those which are time delayed(e.g.,qqq˙(t-d(t))for a variable time delay).

In the control strategies to be developed below,quantized measurements have the following form:

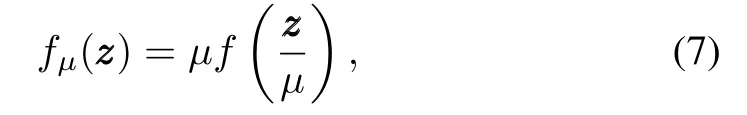
whereµ＞0.The range of the quantizer and the quantization error areHµand Δµ,respectively.µis referred to as the“zoom”variable;increasingµcorresponds to zooming out and essentially obtaining a new quantizer with a larger range and quantization error,whereas decreasingµcorresponds to zooming in and obtaining a quantizer with a smaller range but also a smaller quantization error.

Given the above discussions,the formation control problem can now be stated as follows.

Problem 1.Considering the scenario of remotely controlling a multi-slave bilateral teleoperation system with both quantization and time-varying delays,this paper seeks to design a master-slave formation protocol,such that the master robot can track the centroid of slave agents,while each slave agent can keep a desired relative position vector with the master robot.

Remark1.In single-master-single-slave teleoperation system[4,9,10],the human operator manipulates the master to simulate the motion.The position and velocity signals are then sent to the slave agent so that it can track the motion of the master robot.But it is not simple to track the master′s trajectory,because the effect of environment force is also transmitted back to the master robot,so the teleoperator is said to be controlled bilaterally.In this paper,the singlemaster-multi-slave teleoperation system is considered.In order to track the motion of the master robot,each slave agent should interact with the master robot,while keeping a desired position vector with the master robot.Correspondingly,the master robot is required to control the central location of the formation.Obviously,a simple and effective way is to track the centroid of slave agents for the master robot.Therefore,the above formation objective satisfies the requirement of bilateral teleoperation,and similar formation objective can also be found in[15].

III.MAIN RESULTS

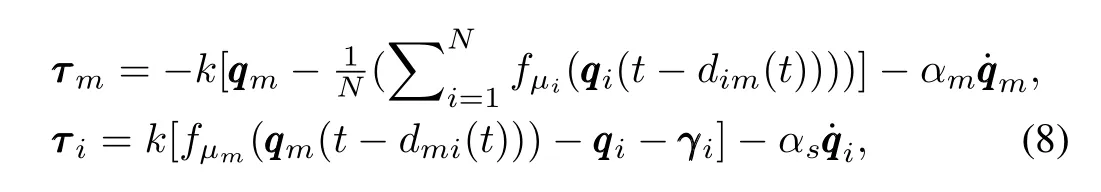
wherek＞0 is the proportional coefficient,αm＞0 andαs＞0 are damping coefficients,fµiandfµmare quantization strategies,andγ i∈Rnis the desired relative position vector.The control framework is shown in Fig.1.

With(1)and(8),the controlled system is rearranged as

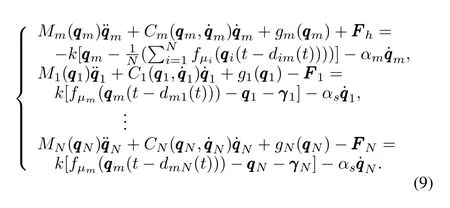
In the following,the stability analysis of the closed-loop system(9)is provided.

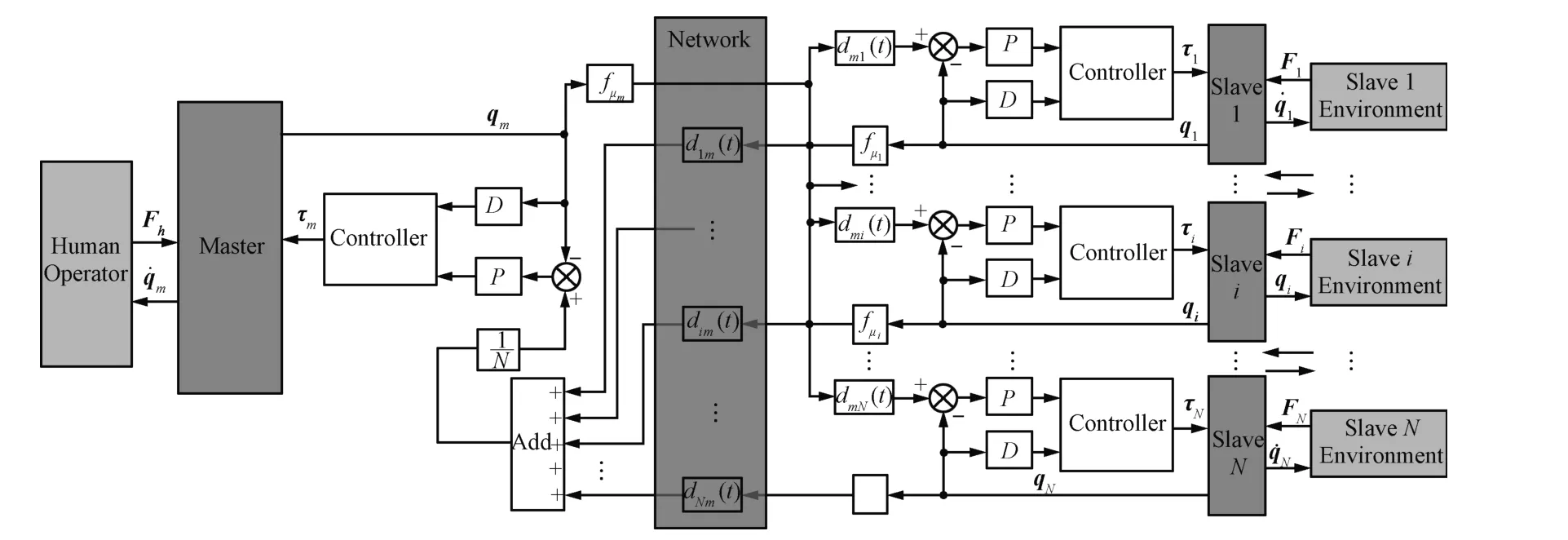
Fig.1. Control framework of the networked teleoperation system.

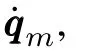
Proof.We choose the following Lyapunov function:

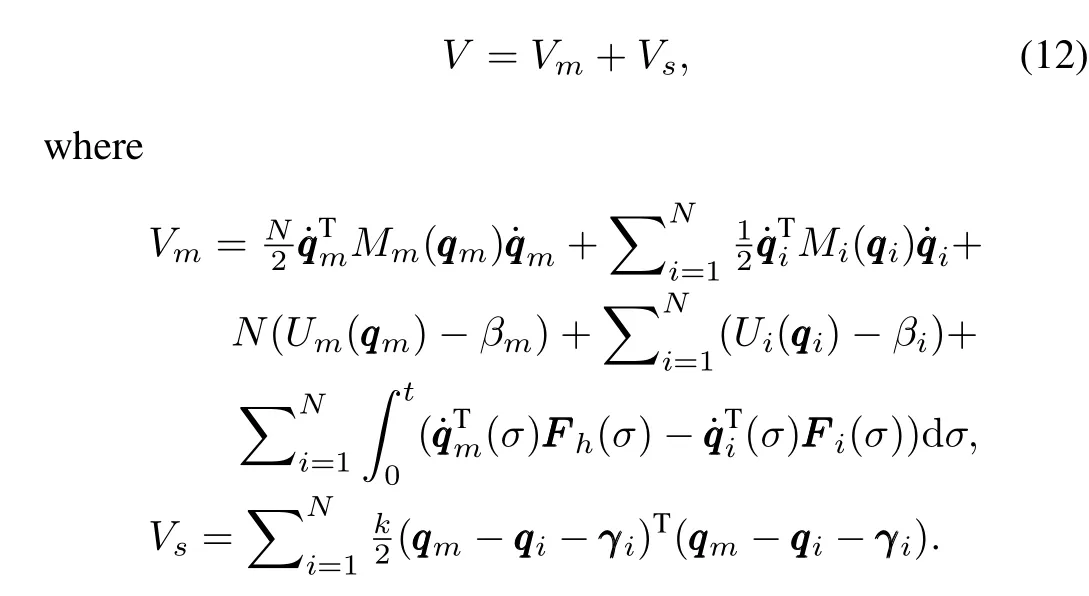
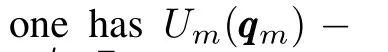
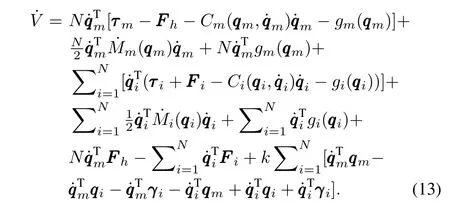
From(6)and(7),one can obtain|(qqqm(t-dmi(t)))/µm|≤Hmand|(qqqi(t-dim(t)))/µi|≤Hi,whereµm＞0 andµi＞0.For the master,the range of quantizer isHmµmand the quantization error is△mµm.For slavei,the range of quantizer isHiµiand quantization error is△iµi.Then,one has

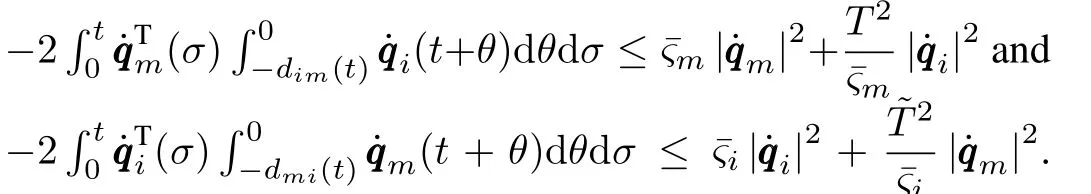
Then,after integrating(17)from zero tot,the derivative ofVis

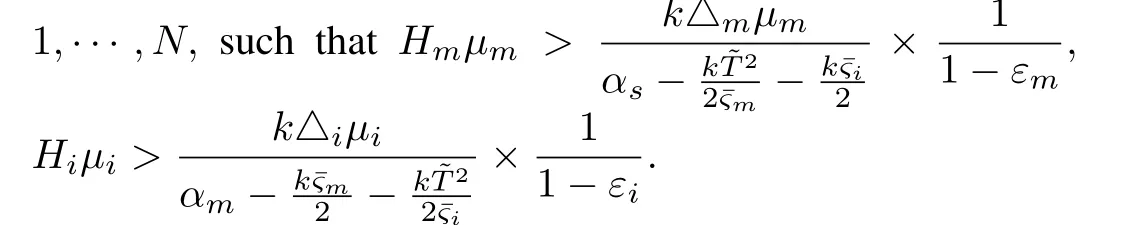
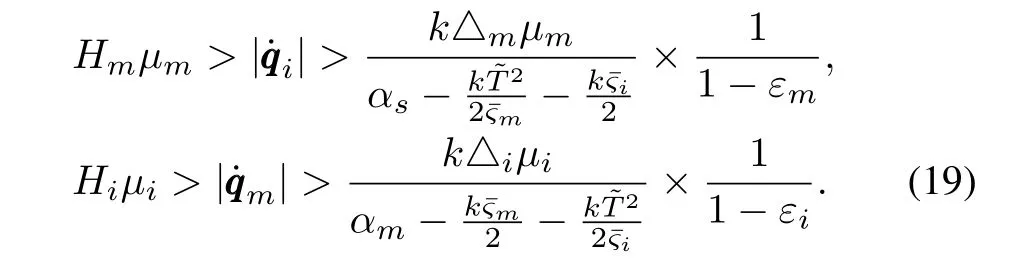
In the following,a special case,where there are no human forceFFFhand environment forceFFFifori=1,···,N,is investigated.Then system(1)is rearranged as

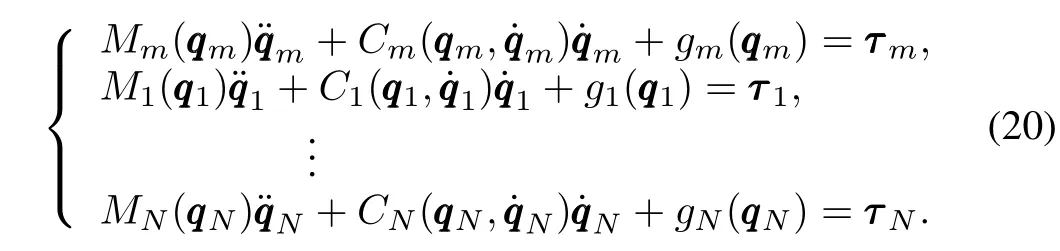
We design the following formation control protocol

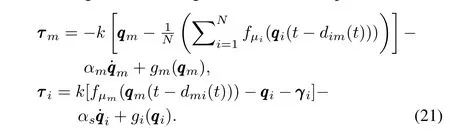
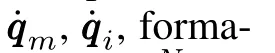
Proof.We choose the following Lyapunov function:

From system(20),one has

A transparent interaction between the operator and environment is need,i.e.,the network contribution of environment should be reflected to the operator under steady-state conditions.

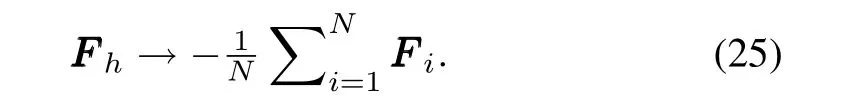
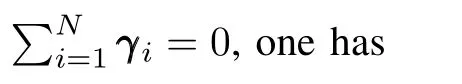
That completes the proof. □

Remark 2.From a theoretic point of view in control,there are two main goals of teleoperation,i.e.,stability and transparency.Different from some previous work,in which only coordination is presented,this paper demonstrates that the teleoperation system satisfies not only synchronization(Theorems 1 and 2)but also transparency(Corollary 1).From Corollary 1,one can see that the human operator senses the torque which exerts on the slave sites by the environment.

Fig.2.Human force input.

IV.SIMULATION RESULTS

The desired formation is a rectangle,and the desired relative position vectors areγ1=(0.5755,0.8178)T,γ2=(-0.8178,0.5755)T,γ3=(-0.5755,-0.8178)Tandγ4=(0.8178,-0.5755)T.Human exerts forceF FFon the master robot inY-direction,which is shown in Fig.2.In the slave site,there is a wall aty= 0.8.When the slave joint reaches the wall and moves further,the feedback force is 4000(y-0.8).With the human force input,the torqueFFFhisJmT(0,1)TFFF,whereJmis the Jacobian matrix of the master manipulator.TorqueFFFiisFFFi=4000(y-0.8)JiT(0,1)T,whereJiis the Jacobian matrix of the salve manipulator fori=1,···,4.The time delays chosen for the simulations aredmi(t)=0.5+0.2sin(t),d1m(t)=0.9+0.5sin(t),d2m(t)=1+0.2sin(t),d3m(t)=0.8+0.7cos(t),andd4m(t)=1+0.6sin(t).

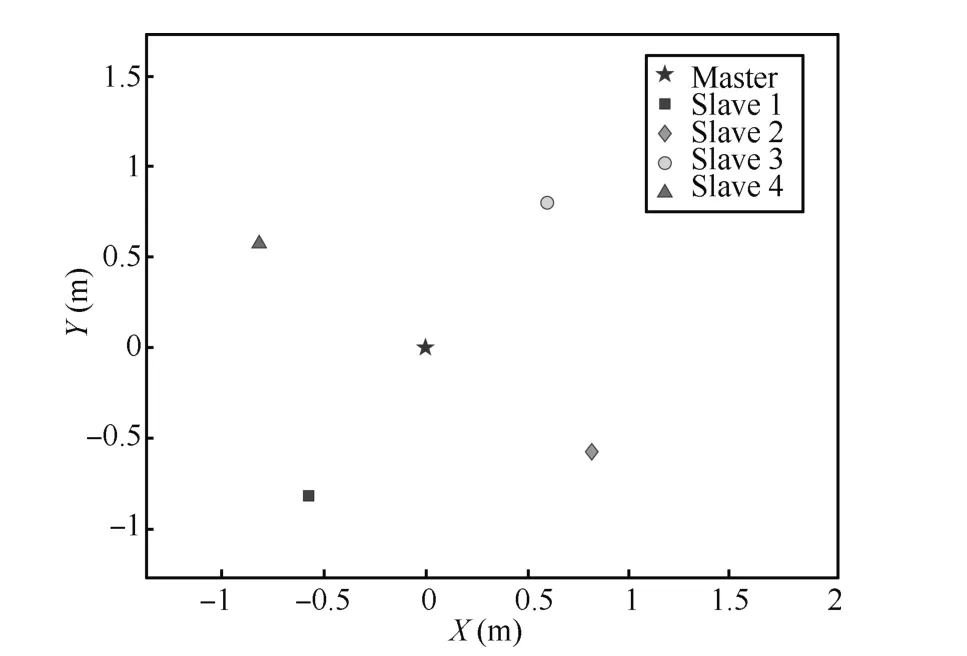
Fig.3.Positions of master and slaves at t=60s.

Fig.4.Position trajectories of master and slaves in X-axis.

Next,it is required to analyze the effect of quantization.Fig.8 shows the original and quantized signals for Joint 1,marked by the dotted and real lines,respectively(to show more clearly,Fig.9 is the enlarged result of Fig.8 from 30 to 40s).Because the quantization error is small,the original and quantized signals look similar.Obviously,the error between the original signal and quantized signal converges to zero with time increasing.

Fig.5.Position trajectories of master and slaves in the Y-axis.

Additionally,the performance comparison for quantization measurements is provided.To facilitate the identification of comparison,the interval ofz8∈[-(H+0.5)Δ,(H+0.5)Δ]is broadened,whereH= 5 and Δ = 0.4.The original signal is designed asz=t-40,t∈[0,8z0].Fig.10 shows the comparison results.In the interval of8∈[-(H+0.5)Δ,(H+0.5)Δ],i.e.,[-2.2,2.2],the quantized signals by using the quantizers in[15-17]are the same as in this paper.However,in the interval ofz8∈(-H,-(H+0.5)Δ)∪((H+0.5)Δ,H),i.e.,(-5,-2.2)∪(2.2,5),the quantization errors in[15-17]are greater than the error in this paper.The smaller error in this paper is attzributed to dynamically adjusted parameterµ,which makesµkeep in the interval of[-(H+0.5)Δ,(H+0.5)Δ].It improves the performance of quantizer and decreases the quantization errors.

Fig.6.Formation errors for master and slaves in X-axis.

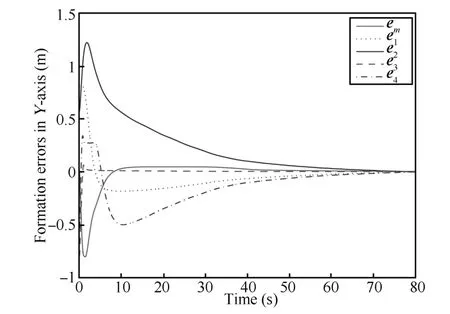
Fig.7. Formation errors for master and slaves in Y-axis.

Fig.8. Original and quantized signals for Joint 1.

Fig.9.Enlarged results of Fig.8 from 30 to 40s.

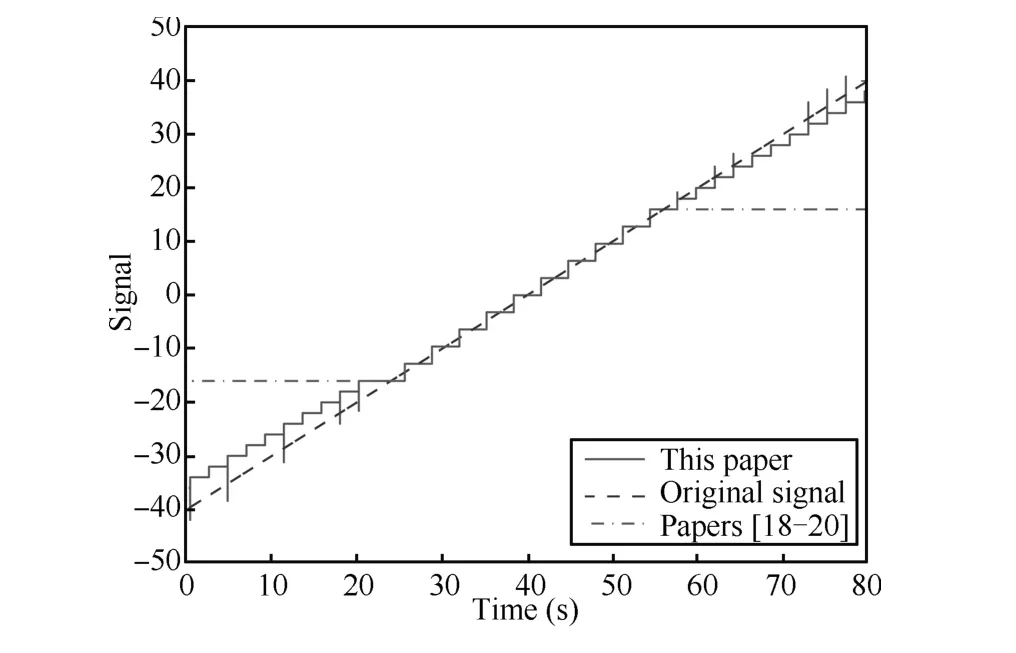
Fig.10.Quantization measurement comparison.

V.CONCLUSION AND FUTURE WORK

In this paper,“multi-agent system”is applied to the teleop-eration system.In addition,a formation controller for singlemaster-multi-slave teleoperation system with time-varying delays and quantization is presented,where the measurement and control signals are quantized before transmission.Sufficient conditions are obtained to show the controller can stabilize the closed-loop single-master-multi-slave teleoperation system.Meanwhile,the formation and tracking tasks can also be achieved with the controller and the sufficient conditions.By operating the master,humans can teleoperate the overall actions of the slave robots while perceiving combined environmental forces on them.Simulation results are provided to show effectiveness of the main results.

Fig.11. Torque error between operator and environment.

Future research directions include motion coordination and stability analysis for delayed collision avoidance control,dynamic flocking and formation.

[1]Pedersen J M,Patel A,Knudsen T P,Madsen O B.Applying 4-regular grid structures in large-scale access networks.Computer Communications,2006,29(9):1350-1362

[2]Chopra N,Spong M W.Bilateral teleoperation:an historical survey.Automatica,2006,42(12):2035-2057

[3]Nuno E,Basanez L,Ortega R.Passivity-based control for bilateral teleoperation:a tutorial.Automatica,2011,47(3):485-495

[4]Ye Y,Liu P X.Improving haptic feedback fidelity in wave-variable-based teleoperation oriented to telemedical applications.IEEE Transactions on Instrumentation and Measurement,2009,58(8):2847-2855

[5]Polushin I G,Liu P X,Lung C H.A control scheme for stable force-reflecting teleoperation over IP networks.IEEE Transactionson Systems,Man,and Cybernetics,Part B:Cybernetics,2006,36(4):930-939

[6]Polushin I G,Liu P X,Lung C H.Projection-based force reflection algorithm for stable bilateral teleoperation over networks.IEEE Transactions on Instrumentation and Measurement,2008,57(9):1854-1865

[7]Nuno E,Ortega R,Barabanov N,Basanez L.A globally stable PD controller for bilateral teleoperators.IEEE Transactions on Robotics,2008,24(3):753-758

[8]Hua C C,Liu P X.Teleoperation over the internet with/without velocity signal.IEEE Transactions on Instrumentation and Measurement,2011,60(1):4-13

[9]Nuno E,Basanez L,Ortega R,Spong M W.Position tracking for nonlinear teleoperators with variable time delay.International Journal of Robotics Research,2009,28(7):895-910

[10]Yang X,Hua C C,Yan J,Guan X P.New stability criteria for networked teleoperation system.Information Sciences,2013,233(1):244-254

[11]Yan J,Guan X P,Luo X Y,Yang X.Consensus and trajectory planning with input constraints for multi-agent systems.Acta Automatica Sinica,2012,38(7):1074-1082

[12]Lin Z Y,Broucke M,Francis B.Local control strategies for groups of mobile autonomous agents.IEEE Transactions on Automatic Control,2004,49(4):622-629

[13]Franchi A,Masone C,B¨uthoff H H,Robuffo P.Bilateral teleoperation of multiple UAVs with decentralized bearing-only formation control.In:Proceedings of the International Conference on Intelligent Robots and Systems.San Francisco,USA:IEEE,2011.2215-2222

[14]Xu Z H,Ma L,Wu Z Y,Schilling K,Necsulescu D.Teleoperating a formation of car-like rovers under time delays.In:Proceedings of the 30th Chinese Control Conference.Yantai,China:IEEE,2011.4095-4101

[15]Rodr´ıguez-Seda E J,Troy J J,Erignac C A,Murray P,Stipanovi´c D M,Spong M W.Bilateral teleoperation of multiple mobile agents:coordinated motion and collision avoidance.IEEE Transactions on Control Systems Technology,2010,18(4):984-992

[16]Kelly R,Santib´anez V,Loria A.Control of Robot Manipulators in Joint Space.London:Springer,2005

[17]Fu M Y,Xie L H.The sector bound approach to quantized feedback control.IEEE Transactionson Automatic Control,2005,50(11):1698-1711

[18]Yang R N,Shi P,Liu G P,Gao H J.Network-based feedback control for systems with mixed delays based on quantization and dropout compensation.Automatica,2011,47(12):2805-2809

[19]Peng C,Tian Y C.NetworkedH∞control of linear systems with state quantization.Information Sciences,2007,177(24):5763-5774

[20]Chun H Y,Fei S M,Yue D,Chen P,Sun J T.H∞quantized control for nonlinear networked control systems.Fuzzy Sets and Systems,2011,174(1):99-113