Distributed Sparse Signal Estimation in Sensor Networks UsingH∞HH-Consensus Filtering

Haiyang Yu Yisha Liu Wei Wang

I.INTRODUCTION

IN recent years,the problems of sparse signal recovery have been widely investigated because of the emergence of new signal sampling theory which is known as compressed sampling or compressed sensing(CS)[1-3].Using less measurements than those required in Shannon sample principle,a sparse signal can be recovered with overwhelming probability by solving a 1-norm minimization problem.This convex optimization problem can be solved by various methods,such as basis pursuit de-noising(BPDN),least absolute shrinkage and selection operator(LASSO),Dantzig selector(DS),etc.Many researchers have attempted to discuss this problem in the classic framework of signal estimation,such as Kalman filtering(KF).In[4],the Dantzig selector was used to estimate the support set of a sparse signal,and then a reduced-order Kalman filter was employed to recover the signal.In[5],the authors presented an algorithm based on a hierarchical probabilistic model that used re-weightedℓ1minimization as its core computation and propagated second order statistics through time similar to classic Kalman filtering.The dual problem of 1-norm minimization was solved in[6]by introducing a pseudo-measurement equation into Kalman filtering,and the Bayesian interpretation of this method was provided in[7].

Distributed sensor network is an important way of data acquisition in engineering,and the distributed estimation or filtering problems have been paid much attention recently[8-10].In[11],three types of distributed Kalman filtering algorithms were proposed.A distributed high-pass consensus filter was used to fuse local sensor measurements,such that all nodes could track the average measurement of the whole network.These algorithms were established based on Kalman filtering in information form,and analysis of stability and performance of Kalman-consensus filter was provided in[12].It is well known that robustness of Kalman filtering is not satisfactory.In[13],a design method of distributedH∞filtering for polynomial nonlinear stochastic systems was presented,and the filter parameters were derived in terms of a set of parameter-dependent linear matrix inequalities(PDLMIs)such that a desiredH∞performance was achieved.AH∞-type performance index was established in[14]to measure the disagreement between adjacent nodes,and the distributed robust filtering problem was solved with a vector dissipativity method.Nevertheless,the distributed sparse signal estimation problem has not been adequately researched yet in the framework ofH∞filtering.

In this paper,we aim to combine the pseudo-measurement method withH∞filtering,and develop a distributedH∞filtering algorithm to estimate a sparse signal sequence using the measurements distributed over a sensor network.Aℓ1-regularizedH∞filter is established at first and the pseudo-measurement equation can be interpreted as a 1-norm regularization term added to the classicH∞performance index.To develop the distributed algorithm,a high-pass consensus filter is embedded intoℓ1-regularizedH∞filter in information form,such that all node filters can reach a consensus on the estimates of sparse signals asymptotically and satisfy the prescribedH∞performance constraint.

The remainder of this paper is organized as follows.Section II gives a brief overview of basic problems in compressed sampling,and introduces the sparse signal recovery method using Kalman filtering with embedded pseudo-measurement.In Section III,the centralizedℓ1-regularizedH∞filtering method is established by means of Krein space Kalman filtering,and the corresponding information filter is derived.A high-pass consensus filter is employed to develop the distributed filtering algorithm in Section IV.Simulation results are given in Section V to demonstrate effectiveness of the proposed method,and Section VI provides some concluding remarks.

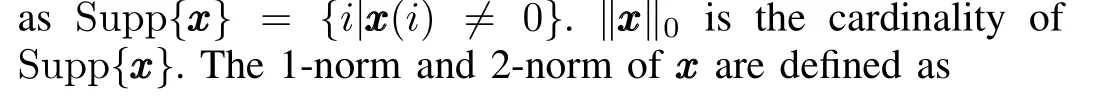
II.SPARSE SIGNAL ESTIMATION USINGKALMAN FILTERING

This section briefly overviews some basic issues in compressed sampling theory,and introduces the pseudo-measurement embedded Kalman filtering method proposed in[6].More details can be found in[1-3,6,7].

A.Sparse Signal Recovery

A signalxxx∈Rnis sparse if‖ xxx‖0≪n,andxxxis calledssparse if‖ xxx‖0=s.Assume{ xxxk}Nk=0is an unknown discretetime sparse signal sequence in Rnandxxxkevolves according to the following dynamic model

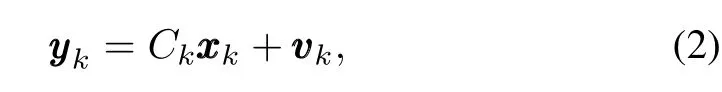
whereCk∈Rm×nis the measurement matrix,and{ vvvk}Nk=0is a zero-mean white Gaussian sequence with covarianceRk≥0.Extracting signalxxxkfrom measurementyyykis an ill-posed problem in general whenm＜n.

As shown in[1-3],xxxkcan be accurately recovered by solving the following optimization problem

But the optimization problem (3)is NP-hard and cannot be solved effectively.Fortunately,the authors of[1]have shown that if the measurement matrixCkobeys the so-called restricted isometry property(RIP),the solution of(3)can be obtained with overwhelming probability by solving the following convex optimization problem

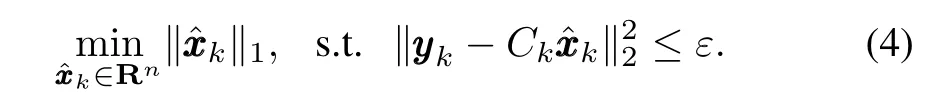
This is a fundamental result in compressive sampling,and one of the deep results is that for as-sparse signal in Rn,only on the order ofm=slognsamples are needed to reconstruct it.

B.Pseudo-measurement Embedded Kalman Filtering

For the system given in(1)and(2),Kalman filtering can provide an estimate ofxxxkwhich is a solution of the following unconstrainedℓ2minimization problem

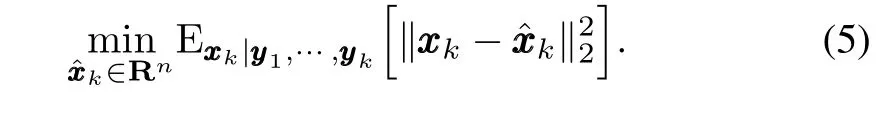
In[6],the authors discussed the stochastic case of(4)

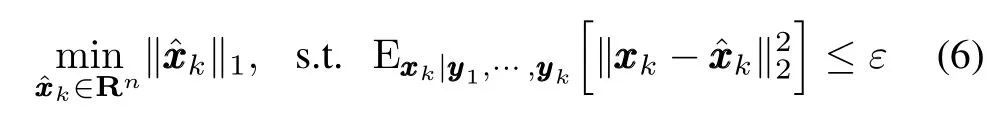
and its dual problem

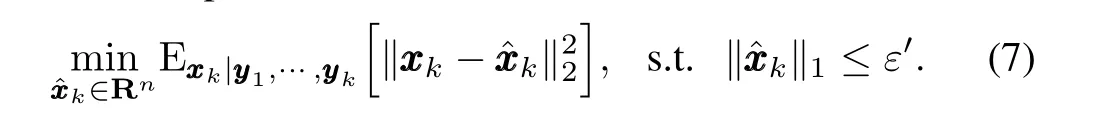
By constructing a pseudo-measurement equation

whereHk=sgn(xxxTk),andε′k～N(0,σk2)serves as the fictitious measurement noise,the constrained optimization problem(7)can be solved in the framework of Kalman filtering and the speci fic method has been summarized as CS-embedded KF with 1-norm constraint(CSKF-1)algorithm in[6].

III.ℓ111-REGULARIZEDHHH∞FILTERING

In this section,the pseudo-measurement equation is combined withH∞filtering,and aℓ1-regularizedH∞filtering is developed for estimating a sparse signal sequence.

Define the augmented measurement equation using(2)and(8)as

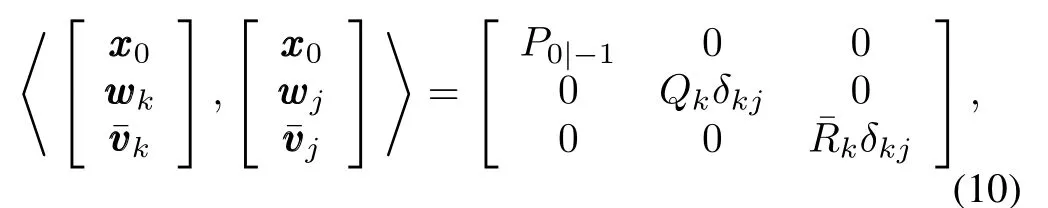
whereδkjis Kronecker delta function.We aim to design a full-order filter in the form of

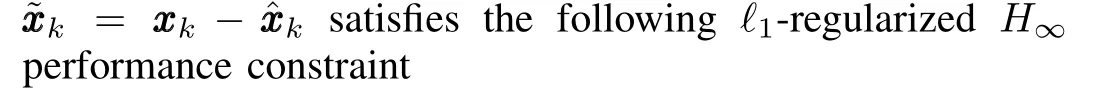
whereγ＞0 is a prescribed scalar.

There exists a filter in the form of(11)achieving the performance(12),if and only if the filtering error covariance matrixPk|ksatisfies

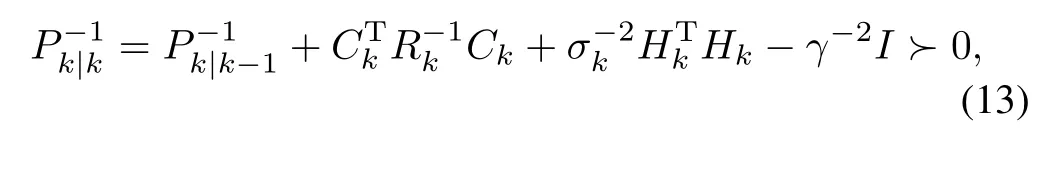
for 0≤k＜N,where the initial value isP0|-1,and the predicted error covariance matrixPk|k-1satisfies the Riccati recursion

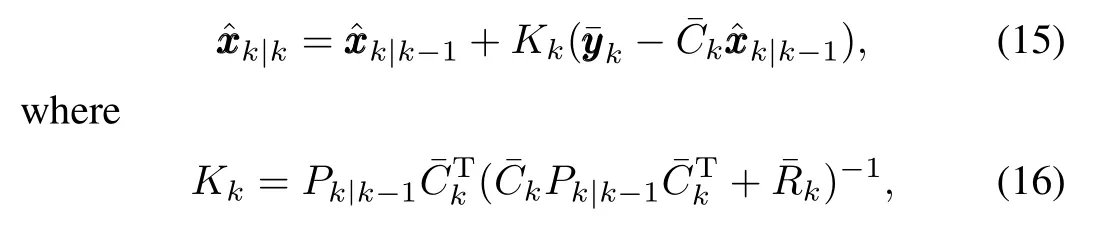
and the predicted estimates

Proof.Define the quadratic performance function

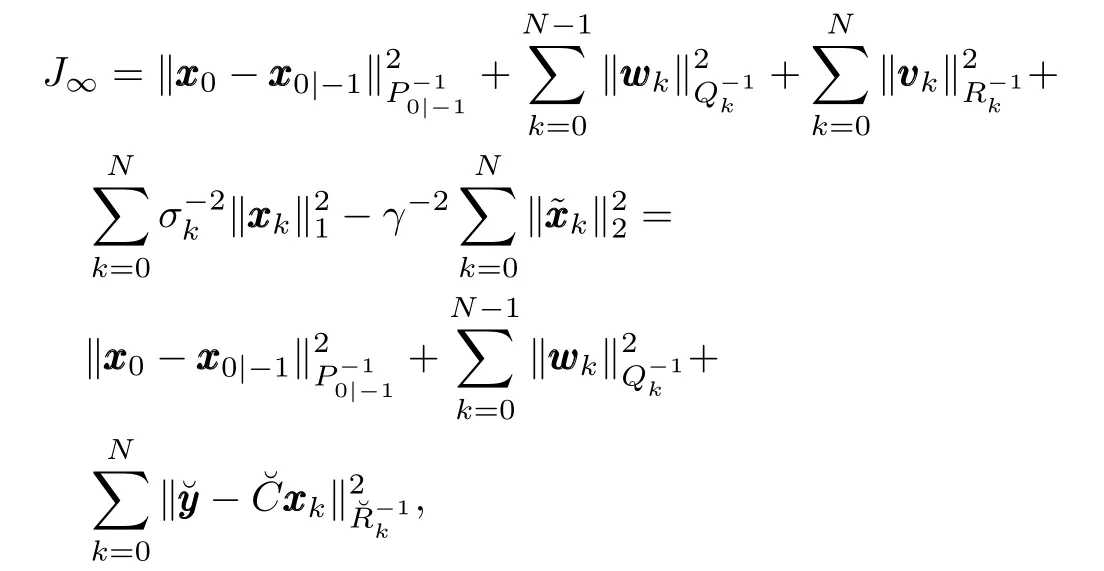
In[7],the pseudo-measurement equation(8)was interpreted in Bayesian filtering framework,and a semi-Gaussian prior distribution was discussed.Here,according to Theorem 1,the pseudo-measurement equation inH∞filtering can be interpreted as a 1-norm regularization term added to the classicH∞performance index.

To establish a distributed filtering algorithm,the result in Theorem 1 will be rebuilt in information form,so by denoting

we can obtain theℓ1-regularizedH∞information filter.

The filter established in Theorem 1 is equivalent to the following information form.

Measurement update:

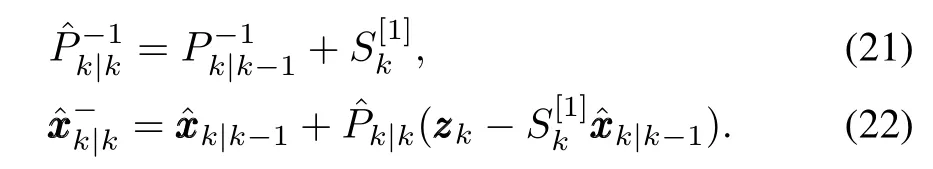
Pseudo-measurement update:

Time update:

Proof.According to matrix inversion lemma,we have

then(15)can be rewritten as

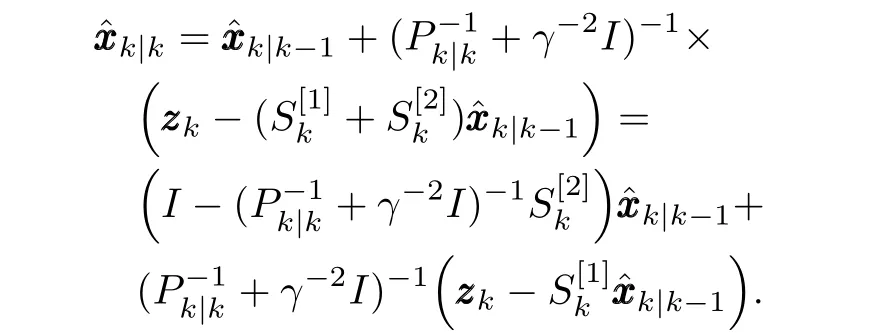
On the other hand,by substituting(22)into(24),we have

It is easy to obtain the following equation

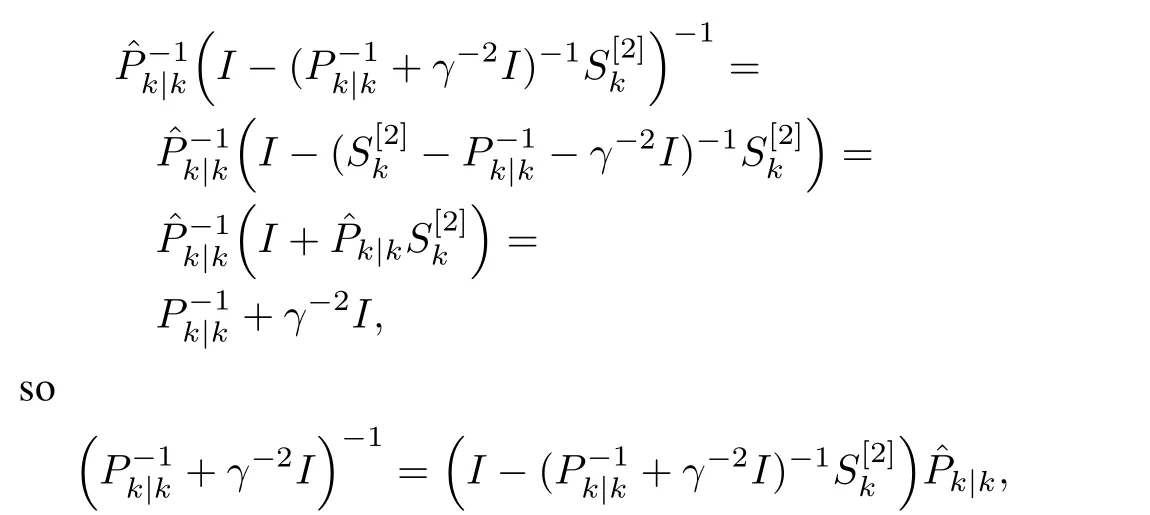
which means(15)is equivalent to(22)and(24).Equation(13)is obtained immediately by combining(21)and(23).□

IV.DISTRIBUTEDH∞HH-CONSENSUS FILTERING WITH PSEUDO-MEASUREMENT

In this section,we will develop a distributedH∞-consensus filtering based on the results presented in Section III.

Consider a sensor network whose topology is represented by an undirected graphG=(V,E,A)of orderrwith the set of nodesV={1,2,···,r},the set of edgesE⊆V×V,and the adjacency matrixA=[aij]r×rwith nonnegative adjacency elementsaij.An edge ofGis denoted by an unordered pair(i,j).The adjacency elements associated with the edges are positive,i.e.,aij＞0⇔(i,j)∈E.Nodejis called a neighbor of nodeiif(i,j)∈Eandj/=i.The neighbor set of nodeiis denoted byNi.AssumeGis strongly connected.

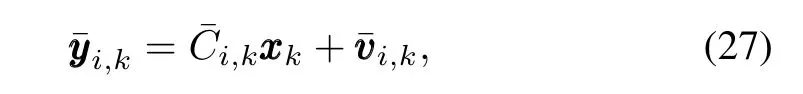
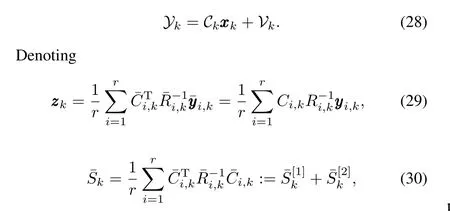
Suppose every node of the network applies the following if lter

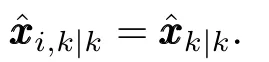
Proof.The proof is a direct combination of Corollary 1 and the result in[11]. □

The distributedH∞filtering can be summarized as the following Algorithm 1.

V.ILLUSTRATIVE EXAMPLE

In this section,we will illustrate effectiveness of the method proposed in Section IV.

Without loss of generality,consider a sensor network with 6 nodes as shown in Fig.1,whose topology is represented by an undirected graphG=(V,E,A)with the set of nodesV={1,2,3,4,5,6},the set of edgesE={(1,1),(1,2),(1,3),(2,2),(2,3),(2,4),(2,5),(3,3),(3,5),(3,6),(4,4),(4,5),(5,5),(5,6),(6,6)},and the adjacency matrix

Fig.1.Topological structure of the sensor network.

Here,we attempt to estimate a 10-sparse signal sequence{ xxxk}inR256and assume the sequence has a constant support set.The dynamics of{ xxxk}can be described by the following linear system

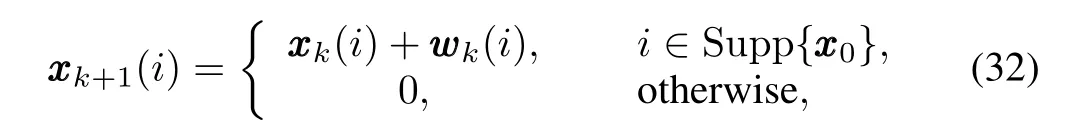
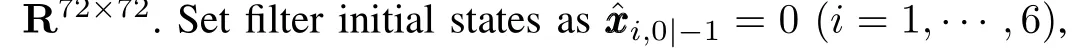
TABLE INMSEs WHEN k=80

Now we are ready to design the distributedH∞filters for system(38).The centralized Kalman filtering and CSKF-1 algorithm proposed in[6]are implemented respectively usingyyycent,CcentandRcent,and we will compare their performances with that of Algorithm 1.The following normalized mean squared error(NMSE)is employed to evaluate the performance,

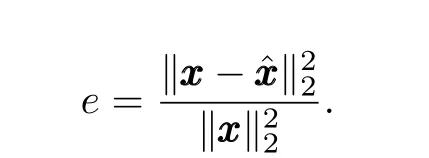
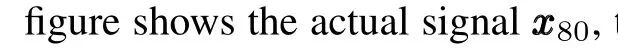
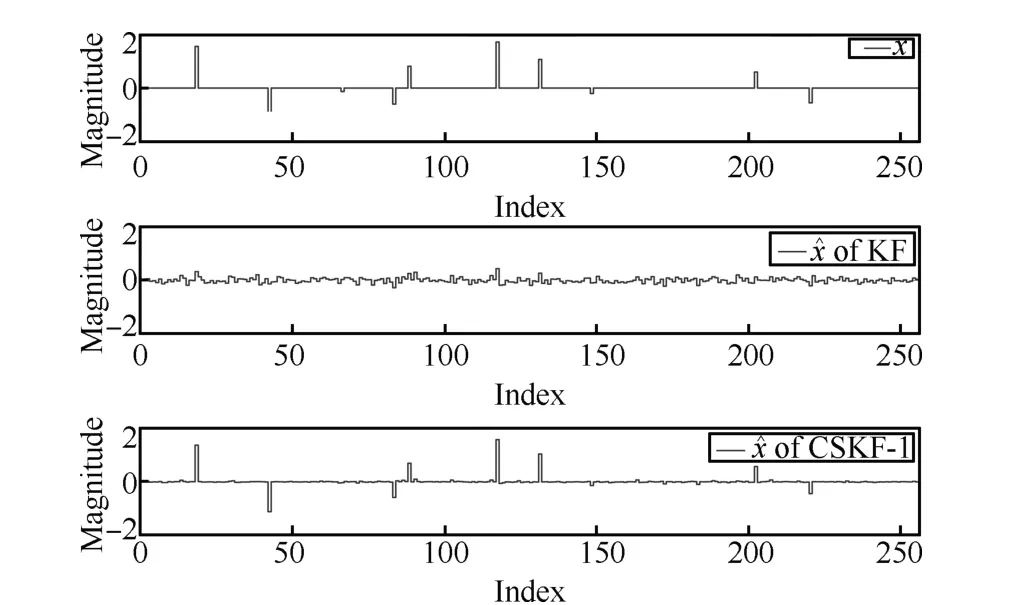
Fig.2. Actual signaland CSKF-1.

VI.CONCLUSION

In this paper,the problem of distributed sparse signal estimation in sensor networks has been considered.The pseudo-measurement equation was interpreted as a 1-norm regularization term in the classicH∞performance index,and theℓ1-regularizedH∞filtering method was proposed.By means of a high-pass consensus filter,the distributedH∞filtering algorithm was established.A numerical example verified effectiveness of the proposed method.However,the algorithm presented in this paper is only suitable to deal with the time varying sparse signal with an invariant or slowly changing support set,and the more general methods need to combine a support set estimator with the filter.The decomposition of sensing matrix needs further research as well.These problems will be discussed in future work.

Fig.3.Estimates of

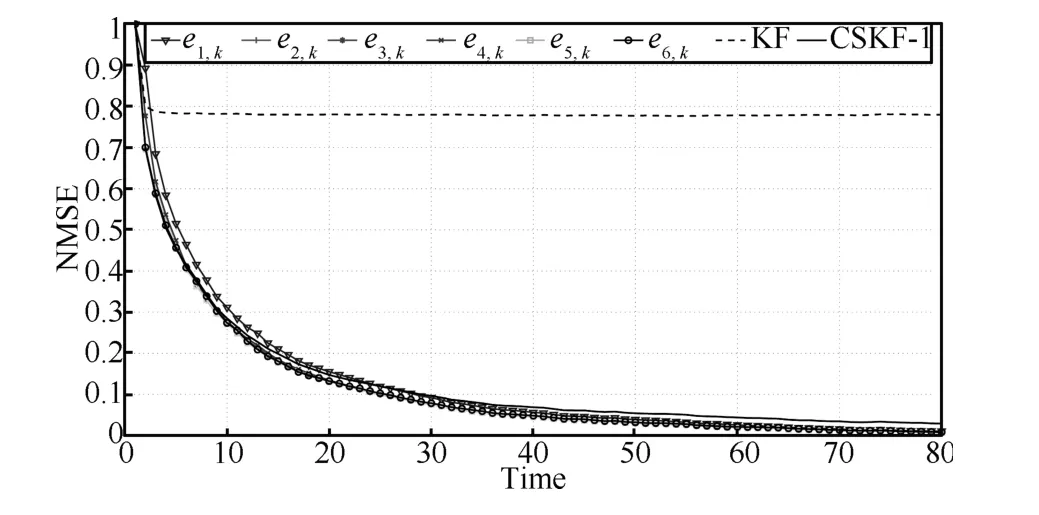
Fig.4.NMSEs of centralized KF,CSKF-1 and Algorithm 1.

[1]Candes E J,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information.IEEE Transactions on Information Theory,2006,52(2):489-509

[2]Candes E J,Romberg J,Tao T.Stable signal recovery from incomplete and inaccurate measurements.Communications on Pure and Applied Mathematics,2006,59(8):1207-1223

[3]Candes E J,Wakin M B.An introduction to compressive sampling.IEEE Signal Processing Magazine,2008,25(2):21-30

[4]Vaswani D.Kalman filtered compressed sensing.In:Proceedings of the 15th IEEE International Conference on Image Processing.San Diego,USA:IEEE,2008.893-896

[5]Charles A S,Rozell C J.Dynamic filtering of sparse signals using reweightedℓ1.In:Proceedings of the 38th International Conference on Acoustics,Speech,and Signal Processing.Vancouver,Canada:IEEE,2013.1-5

[6]Carmi A,Gurfil P,Kanevsky D.Methods for sparse signal recovery using Kalman filtering with embedded pseudo-measurement norms and quasi-norms.IEEE Transactions on Signal Processing,2010,58(4):2405-2409

[7]Kanevsky D,Carmi A,Horesh L.Kalman filtering for compressed sensing.In:Proceedings of the 13th Conference on Information Fusion(FUSION).Edinburgh,UK:IEEE,2010.1-8

[8]Wan Yi-Ming,Dong Wei,Ye Hao.DistributedH∞filtering with consensus strategies in sensor networks:considering consensus tracking error.Acat Automatica Sinica,2012,38(7):1211-1217(in Chinese)

[9]Wang Shuai,Yang Wen,Shi Hong-Bo.Consensus-based filtering algorithm with packet-dropping.Acat Automatica Sinica,2010,36(12):1689-1696(in Chinese)

[10]Feng Xiao-Liang,Wen Cheng-Lin,Liu Wei-Feng,Li Xiao-Fang,Xu Li-Zhong.Sequential fusion finite horizonH∞filtering for Multisenor System.Acat Automatica Sinica,2013,39(9):1523-1532(in Chinese)

[11]Olfati-Saber R.Distributed Kalman filter in sensor networks.In:Proceedings of the 46th IEEE Conference on Decision and Control.Los Angeles,New Orleans,LA:IEEE,2007.5492-5498

[12]Olfati-Saber R.Kalman-consensus filter:optimality,stability,and performance.In:Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference.Shanghai,China:IEEE,2009.7036-7042

[13]Shen B,Wang Z D,Hung Y S,Chesi G.DistributedH∞filtering for polynomial nonlinear stochastic systems in sensor networks.IEEE Transactions on Industrial Electronics,2011,58(5):1971-1979

[14]Ugrinovskii V.Distributed robust filtering withH∞consensus of estimates.Automatica,2011,47(1):1-13

[15]Hassibi B,Sayed A H,Kailath T.Inde finite Quadratic Estimation and Control:a Unified Approach toH2and H∞Theories.Philadelphia:SIAM,1999.