Containment Control of General Linear Multi-agent Systems with Multiple Dynamic Leaders:a Fast Sliding Mode Based Approach
2014-02-07HuiyangLiuLongChengMinTanZengguangHou
Huiyang Liu Long Cheng Min Tan Zengguang Hou
I.INTRODUCTION
IN recent years,there has been an increasing interest in understanding the properties of networked multi-agent systems,which refer to systems of several subunits that exchange information in an effort to perform and carry out a collective task in a decentralized way.It is important to understand the way how these subsystems manage to accomplish a collective behavior,as such phenomena are observed in nature.A large and growing number of researches have been concerned with coordination control of networked multi-agent systems,e.g.,consensus[1-7],formation control[8-11],rendezvous[12,13],coverage control[14,15]and flocking[16,17](more details are referred to[18-20]),partly due to the wide applications of multi-agent systems.
At present,relevant applications utilizing containment control,one type of coordination control,are widespread,e.g.,multi-robot systems and expedition.The study of containment control problems is motivated by numerous natural phenomena and potential applications.For example,the male silkworm moths will end up in the convex hull spanned by all the female silkworm moths by detecting pheromone released by females;a group of heterogeneous robots move from one target to another.Some of the robots do not have the sensing capability to detect obstacles or other robots,while some of the robot team members are highly capable robots that could help to navigate the less capable robots,then a workable strategy would be that the more capable robots guide the less capable robots to deployment positions.Containment control strategies have been investigated a lot[21-30],all of which used traditional approaches.
Sliding mode control is one of the most important approaches in the field of automatic control,and has been widely used in many applications,such as robots,aircrafts,motors,etc.In the multi-agent field,this approach has also drawn some researchers′attention.In[31],distributed coordinated tracking problems of multi-agent systems with single-/doubleintegrator dynamics were proposed and analyzed,where there exists a dynamic virtual leader who is the neighbor of only a subset of a group of followers,all the followers have only local interaction,and only partial measurements of the states of the virtual leader and followers are available.In[32],distributed asymptotic consensus tracking control for linear multi-agent systems with a leader of bounded unknown input was considered.Undirected topologies were considered in all the results above.However,in practice,the network topology might be directed.In addition,the existing terminal sliding mode control may not deliver the same convergence performance when the system state is far away from equilibrium,albeit its finite time convergence lies in its exponentially growing convergence rate when the state is near equilibrium.To get a faster convergence rate,the study on distributed exponential finite time coordination control is necessary.
Motivated by the above discussion,the objective of this paper is to address the following issues.Firstly,under what conditions,a sliding mode control algorithm can be developed to guarantee that the followers converge to the convex hull spanned by the leaders in a finite time exponentially?Secondly,how to design this exponential finite time control algorithm systematically?The main contributions of this paper are listed as follows.
1)A coordination control scheme for multiple linear systems in a general form is studied.Multiple sliding variables are proposed such that all the error trajectories exponentially reach the sliding surfaces in a finite time and then the states of the followers asymptotically converge to the convex hull spanned by the leaders whose control inputs are nonzero and not available to any followers.
2)For both cases of reduced order and non-reduced order,multiple-surface sliding control laws are systematically developed to guarantee the achievement of containment control.
3)The control Lyapunov function for containment control,motivated by the fast terminal sliding mode control,is used to prove reachability of the sliding mode surfaces.
The outline of this paper is as follows.We establish some of the basic notations that will be used in the paper next.In Section II,we list some basic definitions and results.We provide convergence analysis of the underlying network model which can be reduced to the regular form in Section III,and the model which cannot be reduced to the regular form in Section IV,respectively.In Section V,we give some simulation results.Finally,we make a conclusion in Section VI.
Notation.Let0or0m×ndenote an all-zero vector or matrix with compatible dimension,or with the dimension ofm×n.Inis then×nidentity matrix.1nrepresents then-dimensional vector with all the entries being 1.RNandRN×NrepresentN-dimensional real vector space and the set of all theN×Nreal matrices,respectively.Letλ(A)denote one of the eigenvalues of matrixA.sig(x)γ=sgn(x)|x|γ=[sgn(x1)|x1|γ,sgn(x2)|x2|γ,···,sgn(xn)|xn|γ]T,where sgn(·)is the signum function,

and|·|is the absolute value of real numbers.For vectorω=[ω1,ω2,···,ωn]T,letωminandωmaxdenote the minimum and maximum values of{ω1,ω2,···,ωn},respectively.
II.SOME PRELIMINARIES
In this section,we present some definitions and results that will be used in this paper.
Directed graph will be used to model the communication topology between agents[33].LetG=(V(G),E(G),A(G))be a directed graph with the set of verticesV(G) ={v1,v2,···,vn}and the set of edgesE(G)⊆{(vi,vj):vi,vj∈V(G)},where an edge is an ordered pair of vertices inV(G),and the weighted adjacency matrixA(G)=[aij]with nonnegative adjacency elementsaij.An edge ofGis denoted byeij=(vj,vi),wherevjis the parent vertex ofvi,andviis the child vertex ofvj.The adjacency elements associated with the edges are positive,i.e.,eij∈E(G)⇔aij>0.Moreover,we assumeaii=0 for allvi∈V(G).The set of neighbors of nodeviis denoted byNi={vj∈V(G):(vj,vi)∈E(G),j/=i}.
A directed path in a directed graphGis a sequence of vertices,vi1,···,vik,such that(vis,vis+1)∈E(G)fors=1,···,k-1.A directed graphGis strongly connected,if between every pair of distinct verticesvi,vjinG,there is a directed path that begins atviand ends atvj(fromvitovj).
Lemma 1[34].LetA∈Cn×nandA≥0.ThenAis irreducible if and only if the directed graphG(A)is strongly connected.
The Laplacian matrixL=[lij]∈Rn×nofGis defined as

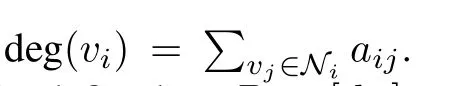
The degree matrix is ann×nmatrix defined asD=[dij],wheredij=deg(vi)fori=j,otherwise,dij=0.Then the Laplacian of the graphGcan be written asL=D-A(G).
Lemma 2[35].A complex matrixM=[mij]∈Cn×nis nonsingular,ifMis irreducible and|mii|≥Pj/=i|mij|for alliwith the inequality strict for at least onei.
Definition 1[36].Communication topologyGis said to satisfy the detail-balanced condition in weights,if there exist some scalarsωi>0,i=1,2,···,n,such thatωjaij=ωiajifor alli,j=1,2,···,n.
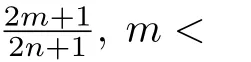

ThenV(x(t))will exponentially reach zero in finite time

Proof.The result can be derived immediately by considering the solution of nonlinear system

The solution of(2)is given below:

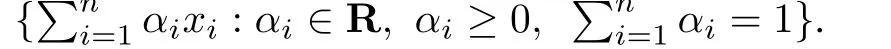
We start with the conventional problem of linear control theory.Suppose that all the agents share a common state spaceRN.Letxi(t)∈RNdenote the state of agentiwhich needs to be coordinated,then the dynamics of agentican be described by

whereA∈RN×N,B∈RN×Mare constant matrices,rank(B)=M,andui(t)∈RMis the control protocol,which can be designed according to the state information available to agenti.The system is assumed to be controllable.
Definition 3[25].For ann-agent system,an agent is called a leader if the agent has no neighbor,and a follower if the agent has at least one neighbor.
In this paper,we assume that there arem(m<n)leaders andn-mfollowers.We denote the set of leaders asRand the set of followers asF.
According to the definitions of leader and follower,Lcan be partitioned as[28]
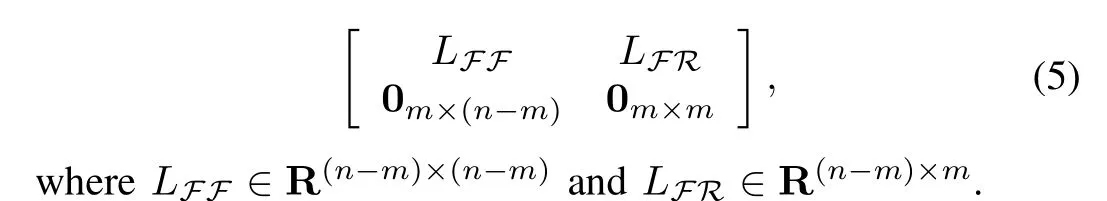
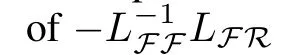
In the two following sections,we will study containment control of multi-agent systems by using the fast sliding mode approach for the reduced order case and the non-reduced order case,respectively.
III.REDUCED ORDER CASE
In this section,we will study containment control of the multi-agent system which can be reduced to the regular form,and show that the containment control problem may be solved in the framework of sliding mode control dealing with a reduced order system.Since rank(B)=M,matrixBmay be partitioned(after reordering the state vector components)as
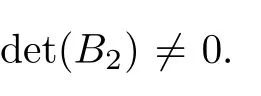

reduces system(4)to the regular form of

wherex1i(t)∈RN-M,x2i(t)∈RM,andAijare constant matrices(i,j=1,2).
We can observe thatx1i(t)in(6)is free of the control inputui(t)which can only influence the dynamics ofx2i(t).The problem of the desired eigenvalue allocation for the original multi-agent system can be transformed after defining the sliding mode motion.The following lemma characterizes this property.
Lemma 4[38].If the pair(A,B)is controllable,the pair(A11,A12)is also controllable.
We list the dynamics of followers and leaders separately in the following:

Here,we assume that all the leaders have the same input,i.e.,uR(t)=1m⊗u0(t),whereu0(t)∈RM,to guarantee that the shape of the convex hull spanned by the leaders is time-invariant.
By handlingx2i(t)as anM-dimensional intermediate control in the first controllable subsystem of(6)with the dimension ofN-Mand choosing proper matrixK∈RM×(N-M),the eigenvalues ofA11may be assigned arbitrarily.That is,by choosing proper feedback gain matrixKin

we can obtain the expected properties ofx1i(t).
Lemma 5.If the pair(A,B)is controllable,then,by choosing an appropriate matrixK,the eigenvalues of matrix in the sliding mode equation
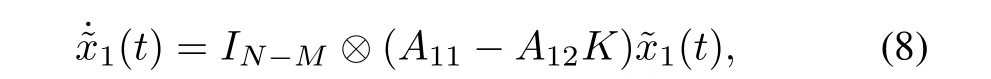
We enforce the sliding mode in the manifold

and its matrix form is

After sliding mode starts,the motion is governed by the reduced-order system(8).Because of controllability of(A11,A12),we can find a control gain matrixK=AT12P,wherePis the unique solution of the following algebraic Riccati equation[39]

We can rewrite(9)as(A11-A12AT12P)TP+P(A11-A12AT12P)+(IN+PA12AT12P)=0,whereby we infer thatIN-M⊗(A11-A12AT12P)is Hurwitz.
How can we bring the error trajectories to the manifolds=0 and maintain it there?The variablessatisfies the equation
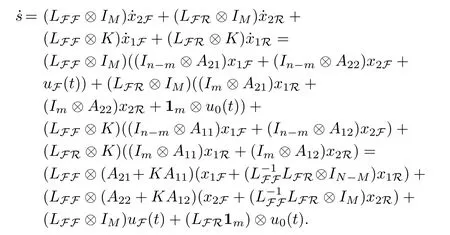
LettingH=LFFΞ,from Lemma 1,Lemma 2 and the definition of detail-balanced condition,we obtain thatHis a positive definite symmetric matrix.The protocol is designed as

which can be written in the matrix form of
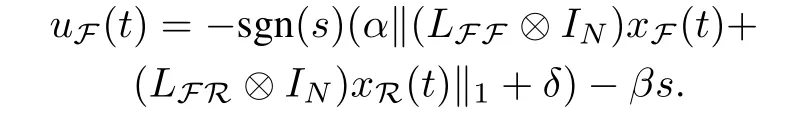
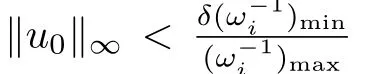
Proof.Calculating the time derivative of the positive definite Lyapunov function

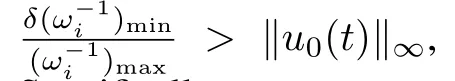

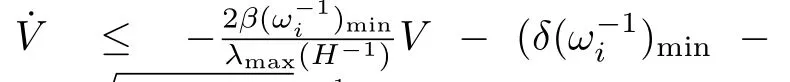
IV.NON-REDUCED ORDER CASE
In this section,we will study containment control of the multi-agent system which cannot be reduced to the regular form,and show that the containment control problem may be solved in the framework of sliding mode control dealing with a non-reduced order system.
For the controllable pair(A,B),the following algebraic Riccati equation[39]
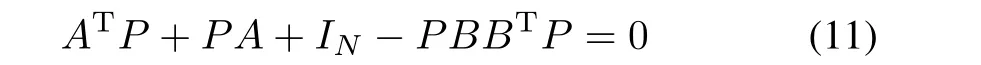
has the unique solutionP=PT>0.
We rewrite the dynamics of leaders and followers in a separate form as

If the system is not reduced to the regular form,we de fine the manifold as

and its matrix form is

Assuming that sliding mode ins=0 has the desired dynamics properties,we have

The fast terminal sliding mode control protocol is designed as

and its matrix form is

Proof.We choose the Lyapunov function as
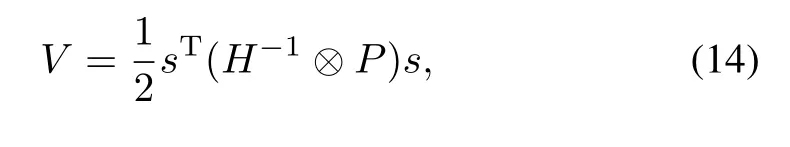
and its time derivative is
V.SIMULATIONS
In this section,we present several simulation results to validate the previous theoretical results.
Example 1.We consider a group of six agents with two leaders,namely,nodes 1 and 2,and four followers,namely,nodes 3~6.The interaction pattern is chosen as Fig.1.The numbers in the circles are the indices of agents,and the numbers near edges are weights.Clearly,the followers′subgraph is strongly connected,and satisfies detail-balanced condition.We choose nodes 3 and 5 as the pinned nodes.
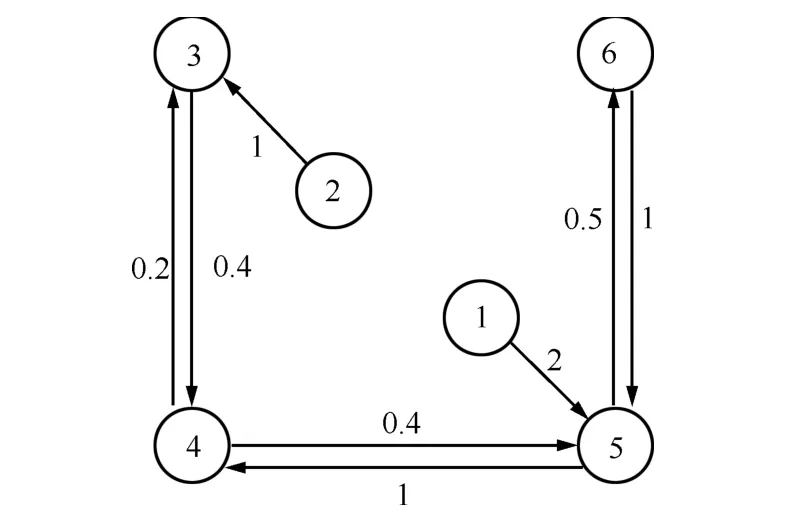
Fig.1.A directed graph with 2 leaders and 4 followers.
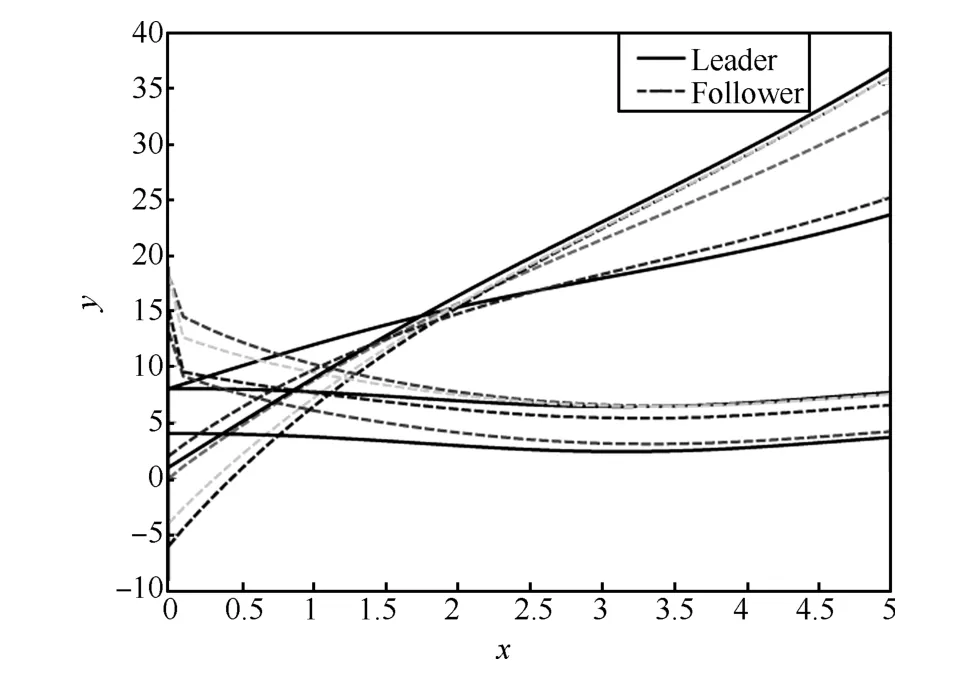
Fig.2.Trajectories of all the agents.

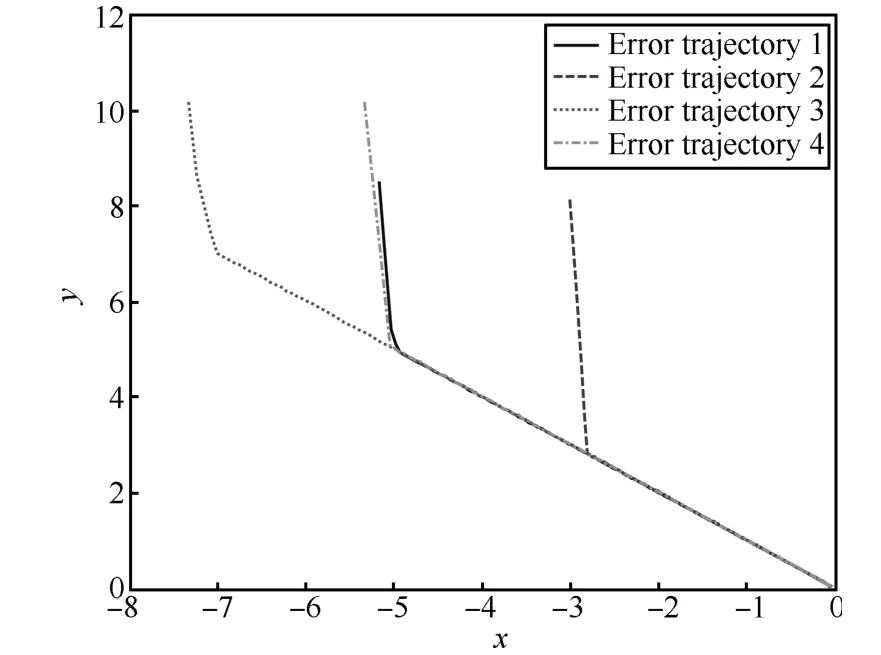
Fig.3.Phase portrait under sliding mode control.
Example 2.We consider a group of six agents with three leaders,namely,nodes 1~3,and three followers,namely,nodes 4~6.The interaction pattern is chosen as Fig.4.
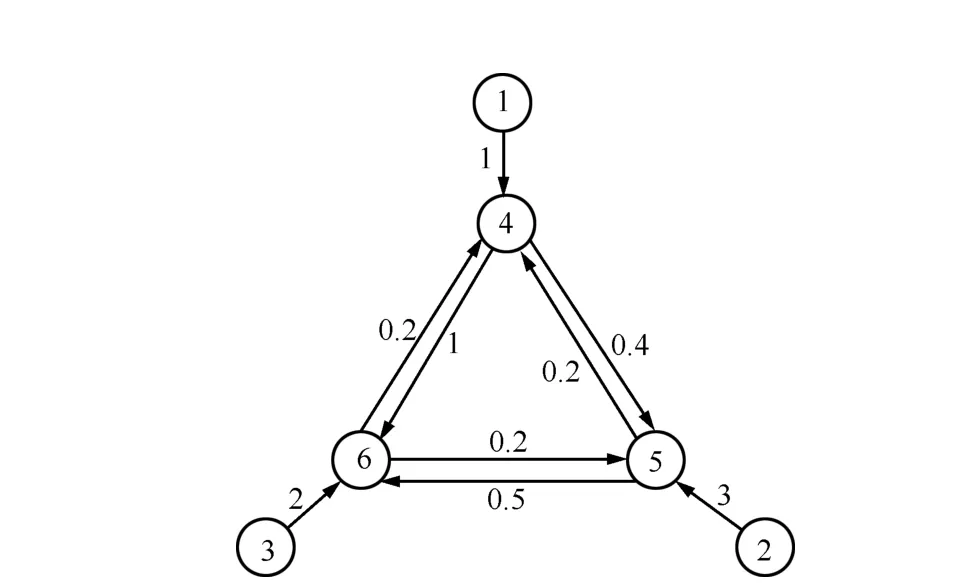
Fig.4. A directed graph with 3 leaders and 3 followers.
Suppose that the leaders and followers have the following dynamics:


Fig.5. Trajectories of all the agents.
From the definition of sliding manifold defined in Section that the followers converge to the convex hull spanned by the leaders.
VI.CONCLUSION
In this paper,containment control problems of general linear multi-agent systems with multiple dynamic leaders have been investigated.The task is to make the followers converge to the convex hull spanned by the multiple dynamic leaders whose control inputs are nonzero and not available to any followers.Based on the relative states of neighboring agents,fast sliding mode controllers have been proposed for both cases of reduced order and non-reduced order.We have shown that the trajectories exponentially reach the sliding mode surfaces if for each follower there exists at least one of the leaders which has a directed path to the follower and the leaders′control inputs are bounded.We have found that the control Lyapunov function for exponential finite time stability is a useful tool to prove reachability of the sliding mode surface.Our future work will focus on discrete-time fast sliding mode control systems.In the future,more efforts will be made on the stochastic containment of general linear multi-agent systems by employing the stochastic approximation technique[40,41].

Fig.6.Phase portrait under sliding mode control.
[1]Jadbabaie A,Lin J,Morse A S.Coordination of groups of mobile autonomous agents using nearest neighbor rules.IEEE Transactions on Automatic Control,2003,48(6):988-1001
[2]Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520-1533
[3]Ren W,Beard R W.Consensus seeking in multi-agent systems under dynamically changing interaction topologies.IEEE Transactions on Automatic Control,2005,50(5):655-661
[4]Cheng L,Hou Z G,Tan M,Lin Y Z,Zhang W J.Neural-network-based adaptive leader-following control for multi-agent systems with uncertainties.IEEE Transactions on Neural Networks,2010,21(8):1351-1358
[5]Hou Z G,Cheng L,Tan M.Decentralized robust adaptive control for the multi-agent system consensus problem using neural networks.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2009,39(3):636-647
[6]Cheng L,Hou Z G,Lin Y,Tan M,Zhang W J.Solving a modified consensus problem of linear multi-agent systems.Automatica,2011,47(10):2218-2223
[7]Yan W S,Li J B,Wang Y T.Consensus for damaged multi-agent system.Acta Automatica Sinica,2012,38(11):1880-1884(in Chinese)
[8]Egerstedt M,Hu X.Formation constrained multi-agent control.IEEE Transactions on Robotics and Automation,2001,17(6):947-951
[9]Lin Z Y,Francis B,Maggiore M.Necessary and sufficient graphical conditions for formation control of unicycles.IEEE Transactions on Automatic Control,2005,50(1):121-127
[10]Yang L,Cao Z Q,Zhou C,Cheng L,Tan M.Formation control and switching for multiple robots in uncertain environments.International Journal of Robotics and Automation,2010,25(3):240-249
[11]Dong X G,Cao X B,Zhang J X,Shi L.A robust adaptive control law for satellite formation flying.Acta Automatica Sinica,2013,39(2):132-141(in Chinese)
[12]Cortes J,Martinez S,Bullo F.Robust Rendezvous for mobile autonomous agents via proximity graphs in arbitrary dimensions.IEEE Transactions on Automatic Control,2006,51(8):1289-1298
[13]Dimarogonas D V,Kyriakopoulos K J.On the rendezvous problem for multiple nonholonomic agents.IEEE Transactions on Automatic Control,2007,52(5):916-922
[14]Gupta P,Kumar P R.Critical power for asymptotic connectivity in wireless networks.In:Proceedings of the 37th IEEE Conference on Decision and Control.Tampa,FL:IEEE,1998.1106-1110
[15]McNew J M,Klavins E,Egerstedt M.Solving coverage problems with embedded graph grammars.In:Proceedings of the 10th International Conference on Hybrid Systems:Computation and Control.Berlin,Heidelberg:Springer-Verlag,2007.413-427
[16]Olfati-Saber R.Flocking for multi-agent dynamic systems:algorithms and theory.IEEE Transactions on Automatic Control,2006,51(3):401-420
[17]Tanner H G,Jadbabaie A,Pappas G J.Flocking in fixed and switching networks.IEEE Transactions on Automatic Control,2007,52(5):863-868
[18]Ren W,Beard R W,Atkins E M.Information consensus in multivehicle cooperative control.IEEE Control Systems Magazine,2007,27(2):71-82
[19]Olfati-Saber R,Fax J A,Murray R M.Consensus and cooperation in networked multi-agent systems.Proceedings of the IEEE,2007,95(1):215-233
[20]Min Hai-Bo,Liu Yuan,Wang Shi-Cheng,Sun Fu-Chun.An overview on coordination control problem of multi-agent system.Acta Automatica Sinica,2012,38(10):1557-1570(in Chinese)
[21]Dimarogonas D V,Egerstedt M,Kyriakopoulos K J.A leader-based containment control strategy for multiple unicycles.In:Proceedings of the 45th IEEE Conference on Decision and Control.San Diego,CA,USA:IEEE,2006.5968-5973
[22]Xiao F,Wang L.Consensus behavior of agents in networked systems under general communication topologies.In:Proceedings of the 2006 IEEE International Symposium on Intelligent Control,2006 IEEE International Conference on Control Applications,Computer Aided Control System Design.Munich,Germany:IEEE,2006.862-867
[23]Liu H Y,Cheng L,Tan M,Hou Z G.Containment control with multiple interacting leaders under switching topologies.In:Proceedings of the 32nd Chinese Control Conference,Xi′an,China:Northwestern Polytechnical University,2013.7093-7098
[24]Ji M,Ferrari-Trecate G,Egerstedt M,Buffa A.Containment control in mobile networks.IEEE Transactions on Automatic Control,2008,53(8):1972-1975
[25]Cao Y C,Stuart D,Ren W,Meng Z Y.Distributed containment control for double-integrator dynamics:algorithms and experiments.In:Proceedings of the 2010 American Control Conference.Baltimore,MD,USA:IEEE,2010.3830-3835
[26]Meng Z Y,Ren W,You Z.Distributed finite-time attitude containment control for multiple rigid bodies.Automatica,2010,46(12):2092-2099
[27]Notarstefano G,Egerstedt M,Haque M.Containment in leader-follower networks with switching communication topologies.Automatica,2011,47(5):1035-1040
[28]Liu H Y,Xie G M,Wang L.Necessary and sufficient conditions for containment control of networked multi-agent systems.Automatica,2012,48(7):1415-1422
[29]Lou Y C,Hong Y G.Target containment control of multi-agent systems with random switching interconnection topologies.Automatica,2012,48(5):879-885
[30]Liu H Y,Xie G M,Wang L.Containment of linear multi-agent systems under general interaction topologies.Systems&Control Letters,2012,61(4):528-534
[31]Cao Y C,Ren W.Distributed coordinated tracking with reduced interaction via a variable structure approach.IEEE Transactions on Automatic Control,2012,57(1):33-48
[32]Li Z K,Liu X D,Ren W,Xie L H.Distributed tracking control for linear multi-agent systems with a leader of bounded unknown input.IEEE Transactions on Automatic Control,2013,58(2):518-523
[33]Biggs N.Algebraic Graph Theory.Cambridge,U.K.:Cambridge University Press,1974
[34]Horn R A,Johnson C R.Matrix Analysis.Cambridge,U.K.:Cambridge University Press,1987
[35]Taussky.A recurring theorem on determinants.American Mathematical Monthly,1949,56(10):672-676
[36]Chu T G,Wang L,Chen T W,Mu S M.Complex emergent dynamics of anisotropic swarms:convergence vs oscillation.Chaos Solutions&Fractals,2006,30(4):875-885
[37]Rockafellar R T.Convex Analysis.New Jersey:Princeton University Press,1972
[38]Utkin V I.Sliding Modes in Control and Optimization.Berlin,Heidelberg:Springer-Verlag,1992
[39]Sontag E.Mathematical Control Theory:Deterministic Finite Dimensional Systems.New York:Springer,1998
[40]Cheng L,Hou Z G,Tan M,Wang X.Necessary and sufficient conditions for consensus of double-integrator multi-agent systems with measurement noises.IEEE Transactions on Automatic Control,2011,56(8):1958-1963
[41]Cheng L,Wang Y P,Hou Z G,Tan M,Cao Z Q.Sampled-data based average consensus of second-order integral multi-agent systems:switching topologies and communication noises.Automatica,2013,49(5):1458-1464
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Modeling and Hybrid Optimization of Batching Planning System for steel making-continuous Casting Process
- Timesharing-tracking Framework for Decentralized Reinforcement Learning in Fully Cooperative Multi-agent System
- Bilateral Teleoperation of Multiple Agents with Formation Control
- Distributed Sparse Signal Estimation in Sensor Networks UsingH∞HH-Consensus Filtering
- Adaptive Nonsingular Terminal Sliding Mode Control Design for Near Space Hypersonic Vehicles
- Distributed Consensus of Multiple Nonholonomic Mobile Robots
