Consensus Robust Output Regulation of Discrete-time Linear Multi-agent Systems

Hongjing Liang Huaguang Zhang Zhanshan Wang Junyi Wang

I.INTRODUCTION

RECENTLY,the study of cooperative control of multi-agent systems has been received much attention from many fields.As an important issue of cooperative control,the agents should be able to reach a common trajectory based on a consensus protocol under the shared information in the presence of information exchange and dynamically changing interaction topologies[1-12].It is widely applied to flocks[1-2],vehicle formations[3]and attitude alignment[4].The central problem is to design a distributed algorithm by which all the agents reach an agreement on their states or outputs,using local information exchange under the communication topologies.The consensus problem of multi-agent systems with leaderless was widely investigated in[5-6].Pioneering contributions to various distributed strategies that achieved consensus were described by[1,3,5].They dealt with consensus problems for networks of dynamic agents under directed networks with fixed and switching topologies and undirected networks with communication time-delays and fixed topology.Diverse applications of consensus problems were discussed in[6]such as fast consensus in small-world networks,and Markov processes load balancing in networked dynamic systems.

In leader-following problems,a subsystem named leader moves along a predefined trajectory,while other subsystems named followers have the same trajectories as the leader[13-19].Reference[15]introduced the optimal tracking problem based on the adaptive dynamic programming method.In many applications,there might exist leaders in the multi-agent networks.However,some variables of an active leader cannot be measured,[16]proposed an “observer”by inserting an integrator into the loop for each agent to estimate the leader′s velocity.Reference[17]considered the leader-following formation problem of multi-robot systems with switching interconnection topologies using dynamic output feedback with the help of a canonical internal model.Kinematics equations of the robots are given in[19]and it uses adaptive control law to solve the robust leader-following formation problem.

A further concept termed output regulation has been introduced to characterize the output consensus of leader-following multi-agent systems.Output regulation theory is to control one or more than one plant so that their outputs can track a reference signal(and/or reject a disturbance)produced by an exosystem.Well-known results about output regulation of linear systems and nonlinear systems have been posed and solved by[20-22].In[23],the tracked signal or rejected disturbance is the same for all the nodes but only partial nodes can access the state information of exosystem and a synchronous manifold method was employed in it.But the majority of existing algorithms use the internal model principle method[24-27].Based on it,a distributed control approach for robust output regulation problem was considered in[24].A general result was given in[27]for linear uncertain multi-agent systems using distributed dynamic state feedback control law and distributed dynamic output feedback control law.Since not all the agents can access the exosystem information,[28-29]gave a dynamic compensator for the un-access part to solve the output regulation problem for heterogeneous agents.

There have been a lot of results about output regulation problem of continuous-time linear or nonlinear multi-agent systems,but few papers dealt with discrete-time multi-agent systems.In view of these issues,this technical note presents a framework on output regulation of discrete-time multi-agent systems.Every subsystem is identical and uncertain.Each agent also has different disturbance.Therefore,we propose an internal model withnadjustable parameters.Then a distributed consensus protocol is given which not only makes the subsystem stable regardless of external disturbance but also regulates the errors to converge to zero.

The outline of this paper is as follows:Section I introduces graph theory and mathematical preliminaries.Then the network models are established.Section II presents the consensus protocols and solves the robust output regulation problem of discrete-time multi-agent systems.An example is given in Section III.Finally,concluding remarks are drawn in Section IV.

Some standard notations of matrix are used throughout this paper.R and C denote the sets of real numbers and complex numbers.The set of positive real numbers is denoted byR+.Rm×nis a set of matrices withmrows andncolumns.For matrixA=[aij]∈Rn×n,A＞0 meansAis a positive definite matrix and the vectorvec(A)is defined byvec(A)=(a11,···,an1,···,a1n,···,ann)T.Givenλ∈C,Re(λ),Im(λ)and|λ|are the real part,the imaginary part and the modulus ofλ,respectively.1n∈Rnis the vector with all entries being 1.

II.PRELIMINARIES AND NETWORK MODELS

A.Basic Knowledge

In this section,some basic concepts and results are introduced.For more details,please refer to[30-31].

1)Graph theory:A weighted digraphG=(V,E,A)of ordernis composed of a vertex setV={v1,v2,···,vn},an edge setE={eij=(vi,vj)}∈V×Vand a weighted adjacency matrixA=[aij]with nonnegative adjacent elementsaij.Moreover,aij＞0 if(vi,vj)∈E,aij=0 if(vi,vj)/∈Eandaii=0 for alli=1,···,n.(vi,vj)∈Eif and only ifith agent can receive information fromjth agent directly.Ni={vj∈V:(vi,vj)∈E}is defined as the set of neighbors of nodevi.In association withG,the in-degree and out-degree of nodeviare defined as follows:

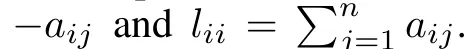
2)Matrix theory:Lemma 1[30].LetA∈Rn×nandλ1,λ2,···,λnbe the eigenvalues ofA.Then forc∈C,λ1+c,λ2+c,···,λn+care the eigenvalues ofA+cIn.

Lemma 2.For any real symmetric matrixQ＞0,there exists real symmetric matrixˇQ＞0 such thatQ=ˇQˇQ.

Proof.From the expression ofQ,there is a real orthogonal matrixUsuch that

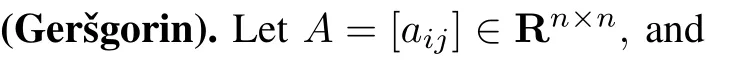
and denote the deleted absolute row sums ofA.Then all the eigenvalues ofAare located in the union ofndiscs

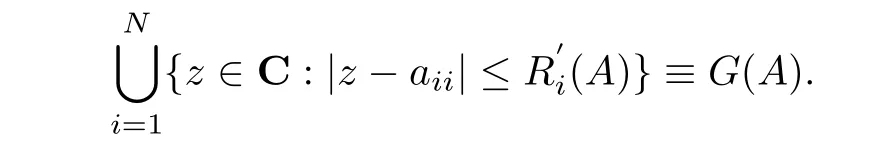
B.Network Models

in whichA0=diag{a10,a20,···,aN0}and¯Asis the adjacency matrix of subgraph¯Gswith vertex set¯Vs=(v1,v2,···,vN).Then the Laplacian matrix¯Lof digraph¯Gis

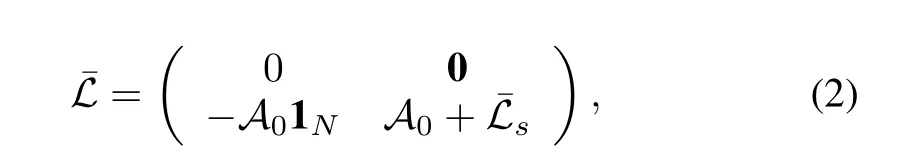
Lemma 4[32].All the eigenvalues ofH=A0+¯Lsdefined in(2)have positive real parts if and only if the digraph¯Gcontains a spanning tree and nodev0as its root.

A group ofNdiscrete-time linear agents with uncertain dynamics are described by

where ΔA, ΔB, ΔCand ΔEiare the perturbations of nominal matricesA,B,CandEi,respectively.It is convenient to identify the system uncertainties with a vector

System(3)with Δ=0 is called a nominal system.

In addition,the reference inputs and the disturbances can be lumped together as the exosystem:

withω†∈Rsdenotingω(k+1)andyr∈Rpthe reference signal.Thus,the consensus output regulation objectives may be prescribed in terms of the tracking errorsei∈Rpas the following form:

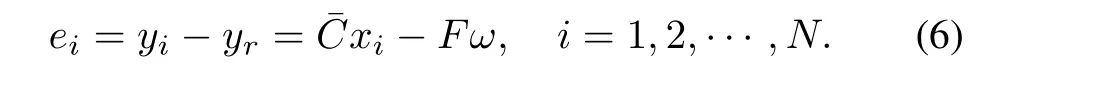
III.CONSENSUS PROTOCOL AND MAIN RESULTS

Assume that each agent can communicate with its neighbor agents and exosystem by sharing their output states.The output-coupling variable relationship between agentiand its neighborsj∈Niis defined as follows:

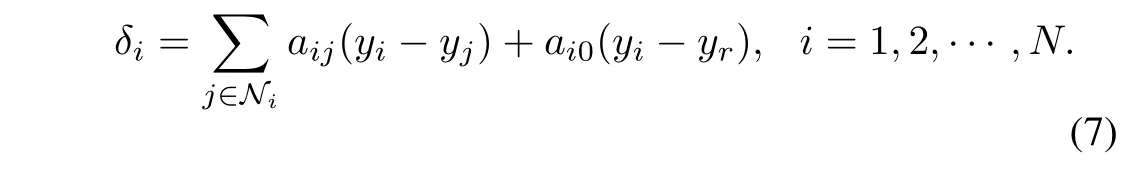
The internal model technique which will be employed to synthesize protocols has important advantages that the parameters of the internal model are not sensitive to the controlled systems[33].It is also necessary to solve the output regulation for uncertain multi-agent systems.Thus,the internal model servocompensatorzi∈Rp(sm)under the network topology is built as follows:

withφi∈R+,i=1,2,···,N.The pair of matrices(G1,G2)is said to incorporate ap-copy internal model of matrixSwith

for alli=1,···,p,andβiis a constant square matrix.σiis a constant column vector such that(βi,σi)is controllable and the minimal polynomial ofSdivides the characteristic polynomial ofβi.

To solve the regulator problem,we give the following distributed consensus protocols:

withi=1,2,···,N,K1∈Rq×n,andK2∈Rq×p(sm)being the gain matrices to be designed later.

Letx=(xT1,xT2,···,xTN)T,z=(zT1,zT2,···,zTN)Tand˜ω=1N⊗ω.Then using protocol(9),the uncertain discrete-time linear dynamics(3)and the internal model servocompensator(8)can be written as

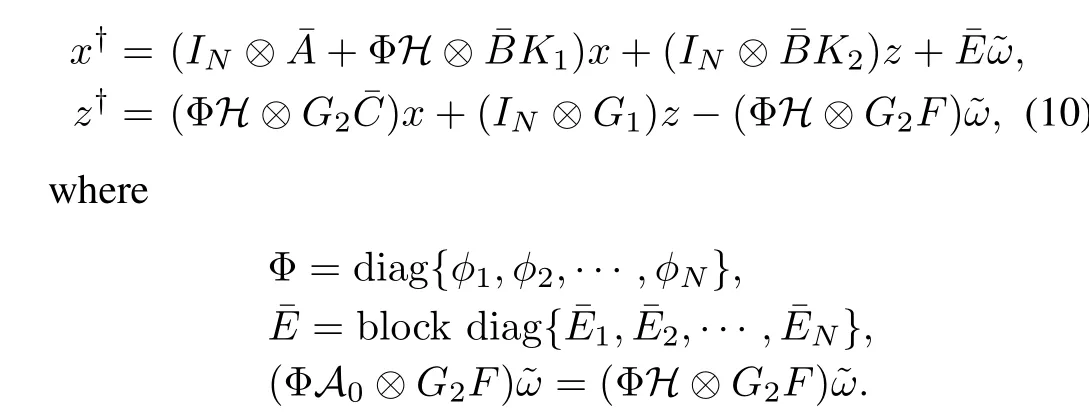
Also,letζ=(xT,zT)T.Then the closed loop system can be written in a compact form as

Problem 1.The robust cooperative output regulation of discrete-time multi-agent systems is solved if there is the consensus protocol(9)such that

2)There exists an open neighborhoodWof Δ=0.For the closed-loop system(11),the local tracking errorei(k)→0 ask→∞,for any initial conditionsxi0∈Rn,ω0∈Rs.

The following basic assumptions and lemmas are necessary to solve the output regulation problem:

Assumption 1.The pair(A,B)is stabilizable.

Assumption 2.Shas no eigenvalues in the interior of the unit circle in thez-plane.

Remark 1.If all the eigenvalues ofSlay in the interior of unit circle in thez-plane,the trajectories ofωwill decay exponentially to zero and not affect the output regulation.Without loss of generality,we assume that all the eigenvalues lay on or out of the unit circle.

Assumption 3.For allλ∈σ(G1),

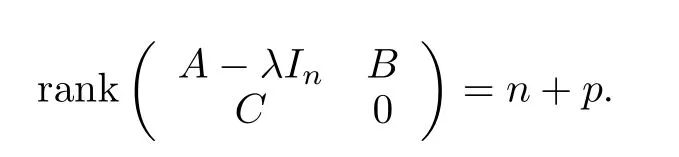
Assumption 4.Digraph¯Gcontains a spanning tree and nodev0as its root.

Lemma 5[33].If Assumptions 1～3 hold,the pair(G1,G2)incorporates ap-copy internal model of matrixS.Let

then pair(A,B)is stabilizable.

Lemma 6[33].Under Assumption 2,assume(G1,G2)incorporates ap-copy internal model ofS.If the matrix equation

has a solution Π2,then Ω =0.

Lemma 7.If(A,B)is stabilizable and the gain matrixKis defined asK=-(BTPB)-1BTPA,then

withP=PT＞0,Q=QT＞0 andQ=ˇQˇQfor symmetric matrixˇQ＞0.Matrix A+sBK,s∈Cis stable if and only ifslies in the stability region

Proof.Since(A,B)is stabilizable,for anyQ=QT＞0,the following discrete-time algebraic Riccati equation:

has a unique solutionP=PT＞0.

Under Lyapunov stability theorem,forP＞0,A+sBKis stable for someKif and only if

Necessity.Since the gain matrixKis defined asK=-(BTPB)-1BTPA,it follows that

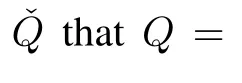
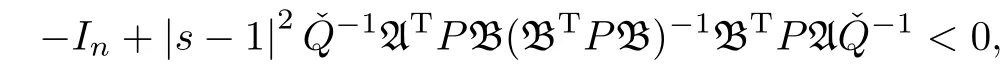
therefore,the stability region is given as

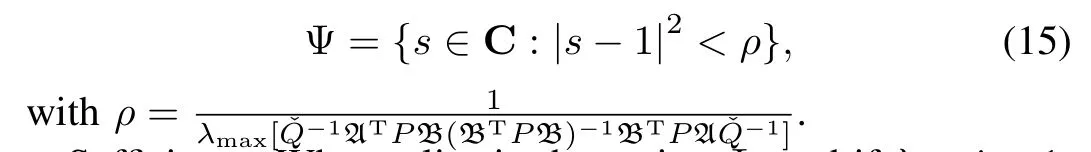
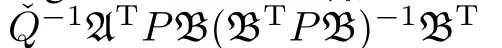
Under Lemma 1,λri|s-1|2-1 are the eigenvalues of

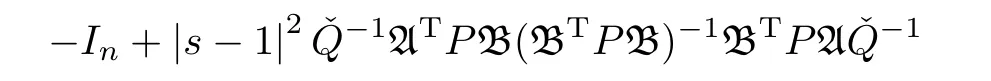
and(16)implies that

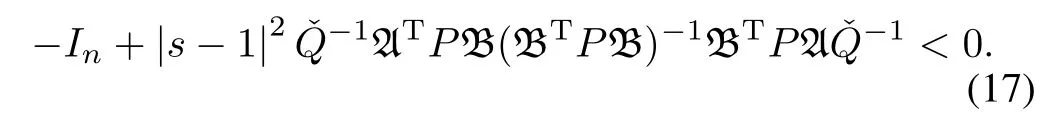
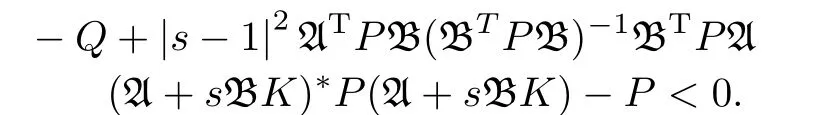
Then A+sBKis stable.

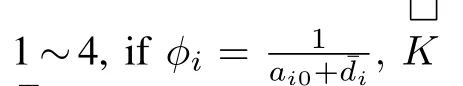
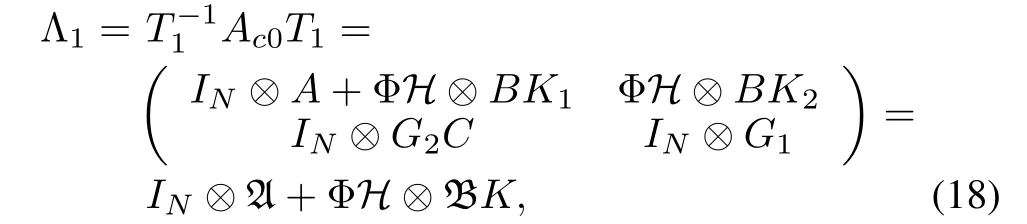
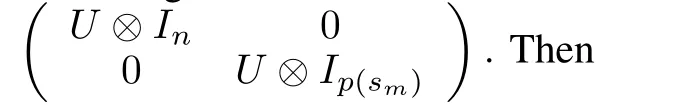
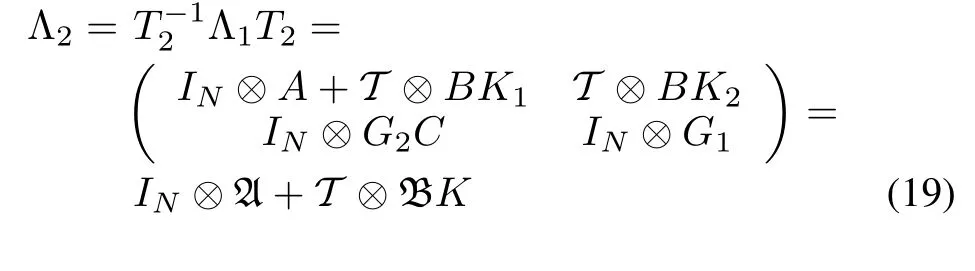
Because the elements of the transformed system matrix Λ2are either block diagonal or block upper-triangular,Λ2is Schur if and only if A+λiBK,i=1,···,Nis Schur.

By the Gerˇsgorin disc theorem,all the eigenvaluesλi,i=1,···,Nof ΦHare located in the union ofNdiscs

which represents that the eigenvalues of ΦHspan in the neighbouring of 1.By Lemmas 5 and 7,the stability region of A+sBKis

If all the eigenvaluesλi,i=1,···,Nare located in Ψ,i.e.,σ(ΦH)⊂Ψ,then A+λiBK,i=1,···,Nis Schur.Therefore,the nominal closed-loop system matrixAc0is Schur.

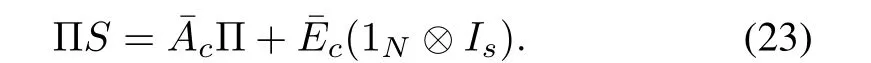
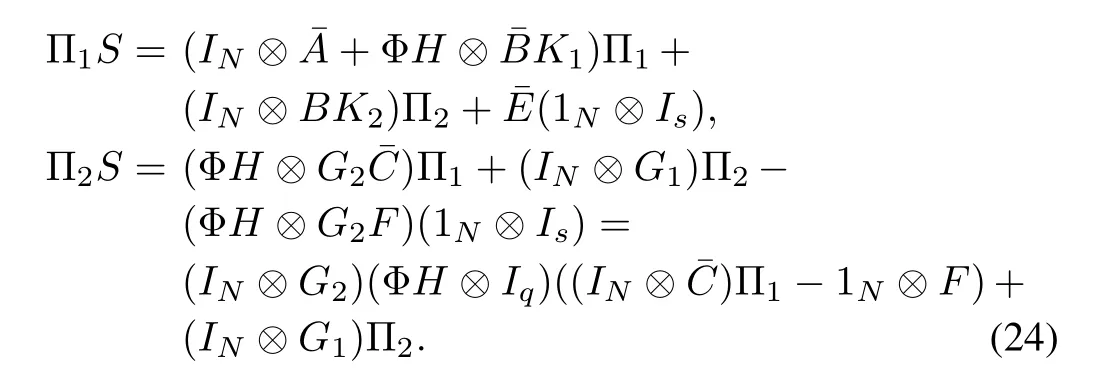
Since(IN⊗G1,IN⊗G2)incorporates apN-copy internal model ofS,under Lemma 6 and by the invertibility of ΦH⊗Iq,one gets

Lete=(eT1,eT2,···,eTN)T.The tracking errors(6)have the following form:

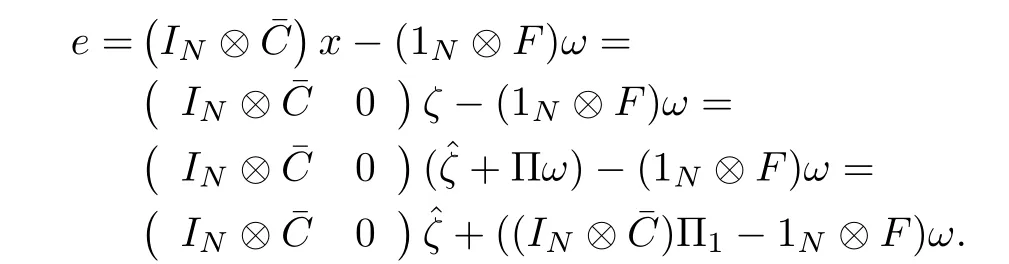
From(25),one gets

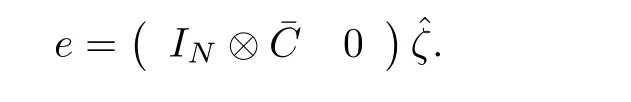
That is,the consensus robust output regulation problem is solved. □

Remark 2.For the system dynamics(3),if Δ=0,robust output regulation problem for uncertain discrete-time multi-agent systems becomes output regulation problem for certain systems.

Remark 3.The robust output regulation for linear multi-agent systems has been deeply studied in[27]and a common gain matrixKcould be found to ensureNnominal closedloop systems stability.We can determine the gain matrix only based on continuous-time algebraic Riccati equation for any system matrix and any information graph.But for discrete-time multi-agent systems,it is hard to find a gainKto make the closed-loop system matrix in the form of A+H⊗BKstable without considering the relationship between system matrix A and Laplacian matrixHof the information graph.Theorem 3.2 in[34]gave the relationship between them that can make the closed-loop system matrix stable.In our paper,parametersφiare used to regulate all the eigenvalues ofHto lie in the neighbor of 1,which can reduce the conservatism.

IV.AN EXAMPLE

In this section,an example is given to validate the effectiveness of the theoretical result.Consider a network of discretetime multi-agent systems described by(3)with

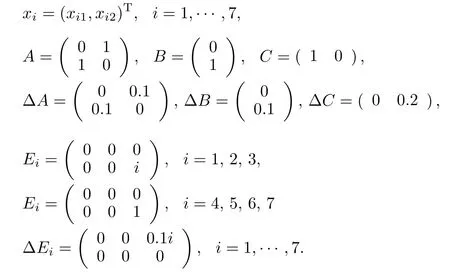
The exosystem is in the form of(5)withω=(ω1,ω2,ω3)Tand

By the exosystem matrixS,we could find a pair of matrices

which incorporate a 1-copy internal model ofS.It is easy to check that Assumptions 1～3 hold.

The system topology is described by the digraph showed in Fig.1 with¯V=(v0,v1,···,v7)and the adjacent weighted values are also showed in Fig.1.Obviously,digraph¯Gcontains a spanning tree and node 0 as its root.The parametric matrix Φ=block diag{1,1,1,1/4,1/2,1,1/4}.By some simple calculations,the stability region is shown as

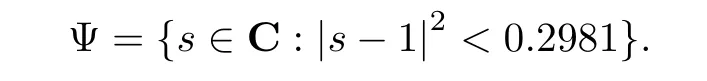
The control gainK1= (-0.4514 0),andK2=(0-0.54860)which can make¯Acstable in an open neighborhood of Δ=0.Thus,we obtain the simulation results as shown in Fig.2.The regulated errors converge to the origin asymptotically.

V.CONCLUSIONS

This paper has investigated the design of distributed consensus protocol for the consensus robust output regulation problem for discrete-time multi-agent systems.A directed graph has been used to describe the information exchange among agents.We assume that the digraph should contain a spanning tree so that all the nodes could communicate with their neighbors and there are no isolated nodes.The internal model method is also used to solve the robust regulation problem.We have also provided an example to illustrate the result.

Fig.1.The communication topology.

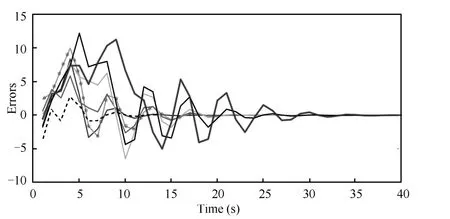
Fig.2.Regulated errors of seven agents.

[1]Jadbabaie A,Lin J,Morse A.Coordination of groups of mobile autonomous agents using nearest neighbor rules.IEEE Transactions on Automatic Control,2003,48(6):988-1001[2]Hong Y G,Gao L X,Cheng D Z,Hu J P.Lyapunov-based approach to multi-agent systems with switching jointly connected interconnection.IEEE Transactions on Automatic Control,2007,52(5):943-948

[3]Fax J A,Murray M R.Information flow and cooperative control of vehicle formations.IEEE Transactions on Automatic Control,2004,49(9):1465-1476

[4]Ren W,Beard R W.Decentralized scheme for spacecraft formation flying via the virtual structure approach.Journal of Guidance,Control,Dynamics,2004,27(1):73-82

[5]Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520-1533

[6]Olfati-Saber R,Fax J A,Murray R M.Consensus and cooperation in networked multi-agent systems.Proceedings of the IEEE,2007,95(1):215-223

[7]Hengster-Movric K,You K Y,Lewis F L,Xie L H.Synchronization of discrete-time multi-agent systems on graphs using Riccati design.Automatica,2013,49(2):414-423

[8]Yang H,Jiang B,Cocquempot V,Zhang H G.Stabilization of switched nonlinear systems with all unstable modes:applications to multi-agent systems.IEEE Transactions on Automatic Control,2011,56(9):2230-2235

[9]Yang H,Jiang B,Zhang H G.Stabilization of non-minimum phase switched nonlinear systems with application to multi-agent systems.Systems and Control Letters,2012,61(10):1023-1031

[10]Hong Y G,Wang X L.Multi-agent tracking of a high-dimensional active leader with switching topology.Journal of Systems Science and Complexity,2009,22(4):722-731

[11]Huang Q Z.Consensus analysis of multi-agent discrete-time systems.Acta Automatica Sinica,2012,38(7):1127-1133

[12]Yan J,Guan X P,Luo X Y,Yang X.Consensus and trajectory planning with input constraints for multi-agent systems.Acta Automatica Sinica,2012,38(7):1074-1082

[13]Wang Y C,Zhang H G,Wang X Y,Yang D S.Networked synchronization control of coupled dynamic networks with time-varying delay.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2010,40(6):1468-1479

[14]Fu J,Zhang H G,Ma T D,Zhang Q L.On passivity analysis for stochastic neural networks with interval time-varying delay.Neurocomputing,2010,73(4-6):795-801

[15]Zhang H G,Liu D R,Luo Y H,Wang D.Adaptive Dynamic Programming for Control-Algorithms and Stability.London:Springer-Verlag,2013

[16]Hong Y G,Hu J P,Gao L X.Tracking control for multi-agent consensus with an active leader and variable topology.Automatica,2006,42(7):1177-1182

[17]Wang X L,Ni W,Wang X S.Leader-following formation of switching multirobot systems via internal model.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2012,42(3):817-826

[18]Hong Y G,Wang X L,Jiang Z P.Distributed output regulation of leader-follower multi-agent systems.International Journal of Robust and Nonlinear Control,23(1):48-66

[19]Liu S C,Tan D L,Liu G J.Robust leader-follower formation control of mobile robots based on a second order kinematics model.Acta Automatica Sinica,2007,33(9):947-955

[20]Francis B A.The linear multivariable regulator problem.SIAM Journal on Control and Optimization,1977,15(3):486-505

[21]Isidori A,Byrnes C I.Output regulation of nonlinear systems.IEEE Transactions on Automatic Control,1990,35(2):131-140

[22]Li R R,Khalil H.Nonlinear output regulation with adaptive conditional servocompensator.Automatica,2012,48(10):2550-2559

[23]Xiang J,Wei W,Li Y J.Synchronized output regulation of networked linear systems.IEEE Transactions on Automatic Control,2009,54(6):1336-1341

[24]Wang X L,Hong Y G,Huang J,Jiang Z P.A distributed control approach to a robust output regulation problem for multi-agent linear systems.IEEE Transactions on Automatic Control,2010,55(12):2891-2895

[25]Wang X L,Han F.Robust coordination control of switching multi-agent systems via output regulation approach.Kybernetika,2011,47(5):755-772

[26]Wieland P,Sepulchre R,Allg¨ower F.An internal model principle is necessary and sufficient for linear output synchronization.Automatica,2011,47(5):1068-1074

[27]Su Y F,Hong Y G,Huang J.A general result on the robust cooperative output regulation for linear uncertain multi-agent systems.IEEE Transactions on Automatic Control,2013,58(5):1275-1279

[28]Su Y F,Huang J.Cooperative output regulation of linear multi-agent systems.IEEE Transactions on Automatic Control,2012,57(4):1062-1066

[29]Su Y F,Huang J.Cooperative output regulation with application to multi-agent consensus under switching network.IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2012,42(3):864-875

[30]Horn R A,Johnson C R.Matrix Analysis.Cambridge,UK:Cambridge University Press,1987

[31]Godsil C,Royle G.Algebraic Graph Theory.New York:Springer-Verlag,2001

[32]Li Z K,Duan Z S,Chen G R,Huang L.Consensus of multi-agent systems and synchronization of complex networks:a unified viewpoint.IEEE Transactions on Circuits and Systems I:Regular Papers,2010,57(1):213-224

[33]Huang J.Nonlinear Output Regulation:Theory and Applications.Phildelphia,PA:SIAM,2004

[34]You K Y,Xie L H.Network topology and communication data rate for consensusability of discrete-time multi-agent systems.IEEE Transactions on Automatic Control,2011,56(10):2262-2275