Distributed Force/Position Consensus Tracking of Networked Robotic Manipulators
2014-02-07LijiaoWangBinMeng
Lijiao Wang Bin Meng
I.INTRODUCTION
DISTRIBUTED control of networked robotic manipulators has gained significant attention in recent years.The motivation of the research is that a multi-robot approach offers several advantages,such as parallel execution of tasks,robustness by adding redundancy,and elimination of the single point of failure that is present in single robot systems[1],etc.The major purpose of distributed control is to achieve a global group behavior with only local interaction.Distributed control scheme performed on multi-robot networks can provide great benefits with lower cost,higher versatility and easier maintenance[2].Consensus,as a fundamental problem in distributed control,means that a group of vehicles reach an agreement on a common value by interacting with their local neighbors.
The robotic agent in this paper is modeled as the fully actuated Euler-Lagrange system.The studies on distributed control of multiple Euler-Lagrange systems mainly focus on the position coordination problems[3-10].The consensus tracking problem with a single or multiple dynamic leaders is considered in[6-8,10].In[6],a unified extended Slotine and Li controller is proposed for both leaderless consensus and consensus tracking in the presence of dynamic uncertainties on directed graphs with a spanning tree.Cascaded framework is introduced which provides a convenient approach to handle the consensus problem.Yet,for the tracking case,the desired trajectory is assumed to be available to all the agents.To remove this assumption,a distributed sliding mode estimator which aims at estimating the desired trajectory in a distributed manner is constructed in[7]for multiple linear agents,and then extended to multiple Euler-Lagrange systems with dynamic uncertainties in[8]for directed graphs containing a spanning tree.The work of[9]develops the cascaded framework in[6],and solves task-space consensus problem on strongly connected graphs.The work of[10]further proposes an adaptive task-space position observer such that task-space velocity-free synchronization on directed graphs containing a spanning tree can be achieved.
Nevertheless,the above literature concentrates on the distributed position control in free space without considering the case when the robots interact with the environment.In practical applications,such as inspection,assembly,polishing,grinding as well as scribing,the end-effectors of the robot manipulators are usually required to be in contact with the environment,which involves the interactive force between the manipulators and the environment.In order to realize safe and elaborate operation in the presence of uncertainties,various adaptive force/position control laws are developed for single robotic agent[11-15],aiming at controlling both the position of the end-effector in the unconstrained direction and its contact force with the environment in the constrained direction.Adaptive force control is proposed in[11]to estimate unknown environment stiffness with exact environment position when the robot inertia matrix is constant.In[12],adaptive control is also used to deal with stiffness uncertainties after fully linearizing and decoupling system dynamics.The work of[13]proposes a passivity-based adaptive law to cope with stiffness uncertainties of the environment by use of a scalar factor,while the robot model and surface position are required to be exactly known.The work of[14]takes both stiffness uncertainties and surface kinematic uncertainties into account,and devises a new adaptive force/position tracking controller for a soft robot finger in compliant contact with a rigid flat surface when the dynamic parameters of the robot are exactly known.
When it comes to large-scale assembly tasks in modern manufactures and space applications,multiple robot manipulators may perform tasks in a common environment and the research of distributed force control becomes as significant as distributed motion control in these cases.Another example is that when multi-robots push or carry a common flat object,they must coordinate both position and force to realize movement of the object without rotating or tumbling.Therefore,it is necessary to consider the force synchronization problem in many applications due to the requirement of a balanced movement.The work of[15]considers multiple mobile manipulators grasping a common object in contact with a rigid surface,and proposes an adaptive robust control law in a cooperative manner,but not in a distributed manner.In addition,when the environment is compliant,the methods in rigid condition are no longer applicable,since the bouncing effect caused by the contact force can eventually lead to instability of the manipulators[16].To our best knowledge,no work has focused on distributed compliant force control of networked robotic manipulators.When the information topology is directed with a spanning tree and uncertain environment and robotic dynamics are considered,due to the asymmetric Laplacian matrix,the nonlinearities and uncertainties of the robot-environment model,the distributed force control scheme is not a straightforward extension of the single agent case.
In this paper,we consider the force synchronization problem in constrained space,where multiple robotic manipulators on directed graphs interact with uncertain compliant environment.We propose a distributed adaptive hybrid controller such that force and free-space position asymptotically synchronize to the convex hull constituted by the leaders under directed graphs containing a spanning tree.A novel adaptive force observer is constructed to achieve force synchronization in the presence of environment uncertainties,which further removes the requirement to measure force derivatives.In addition,by defining an appropriate force reference signal,our strategy eliminates the reliance on the estimation of surface distance,thus avoiding overparamterization in the kinematic loop design.The proposed scheme has a quite simple and direct form in a cascaded framework.
Notation.In the subsequent sections,if there are no special illustrations,(ˆ·)denotes the estimation of(·),(˜·)=(ˆ·)-(·),and Δ(·)=(·)-(·)dwith(·)dbeing the desired value of(·).In addition,1mand0mdenotem×1 column vector containing all ones and all zeros respectively,andImdenotes them×midentity matrix.
II.PRELIMINARIES AND PROBLEM DESCRIPTION
A.Robotic Dynamics and Kinematics
We considermrobotic followers labeled as agents 1 tom,interacting with flat compliant environment.The single-agent model is illustrated in Fig.1.The dynamic model of theith follower in joint space ignoring friction forces can be written as[14]
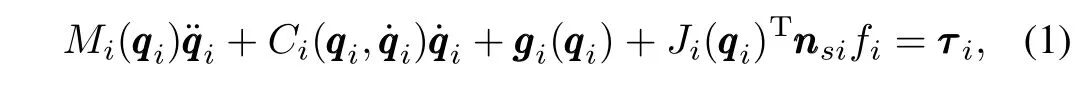


Fig.1.A robot manipulator interacting with a flat compliant surface.
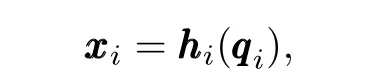


We proceed to get the deformation of the compliant environment as[14]

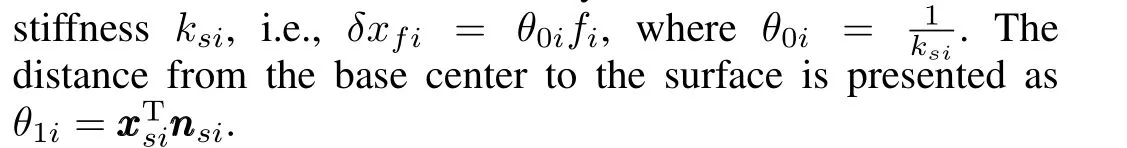

and the task-space velocity

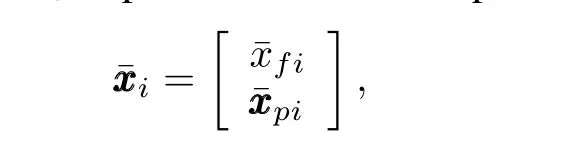
As a result,(1)can be reformulated as

It is well known that the dynamics(4)have the following properties[18].



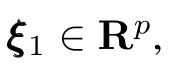
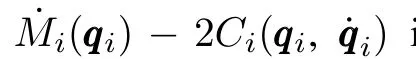
B.Graph Theory
We assume there areNagents withmrobotic followers andN-mvirtual leaders.Let the vertexidenote theith agent and the vertex setV={1,···,N}.The edge(i,j)denotes the information flow between agentsiandj.LetEdenote the edge set.An edge(j,i)∈Emeans that agentican obtain information from agentj.The vertex sets for the followers and leaders are denoted byVF={1,···,m}andVL={m+1,···,N},respectively.The following assumption is made for the information topology.
Assumption 2.For each follower,there exists at least one leader that has a directed path to the follower.
The adjacency matrixW=[wij]∈RN×Nassociated with the interaction graphEis defined aswij>0 if(j,i)∈E,andwij=0,otherwise.We assume the self edges do not exist,i.e.,wii=0.Then we define the Laplacian matrixL=[ℓij]∈RN×Nas
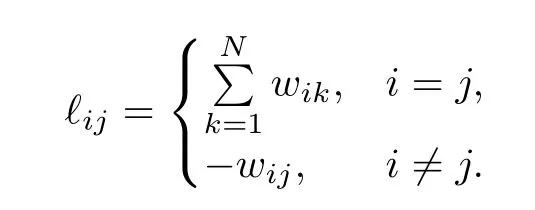
Here,Lhas the form of[8]

whereL1∈Rm×mandL2∈Rm×(N-m)satisfy the following lemma.
Lemma 1[8].The matrixL1is non-singular,and all eigenvalues ofL1have positive real parts,if and only if Assumption 2 holds.Moreover,each entry of-L-11L2is nonnegative,and all row sums of-L-11L2equals to one,if Assumption 2 holds.

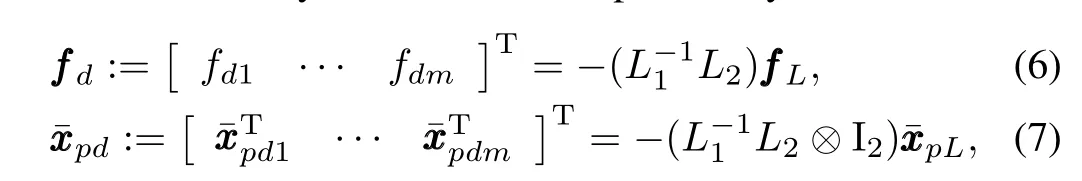
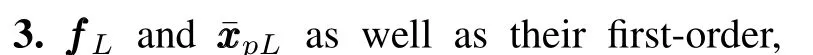
III.THE DESIGN OF FORCE/POSITION CONSENSUS TRACKING CONTROLLER
In this section,we give the cascaded structure design scheme,which divides the overall system into kinematic module and dynamic module.The kinematic loop is first constructed to achieve force/position synchronization and to get a reference joint-space velocity for the controller,while the dynamic loop is to pose the control law such that the conditions required for the kinematic loop design are satisfied.
A.Kinematic Loop Design
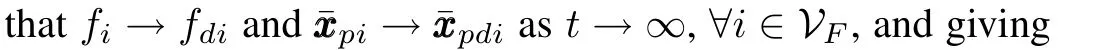
We first construct the sliding mode estimators to estimate the desired trajectory in a distributed manner[7],i.e.,
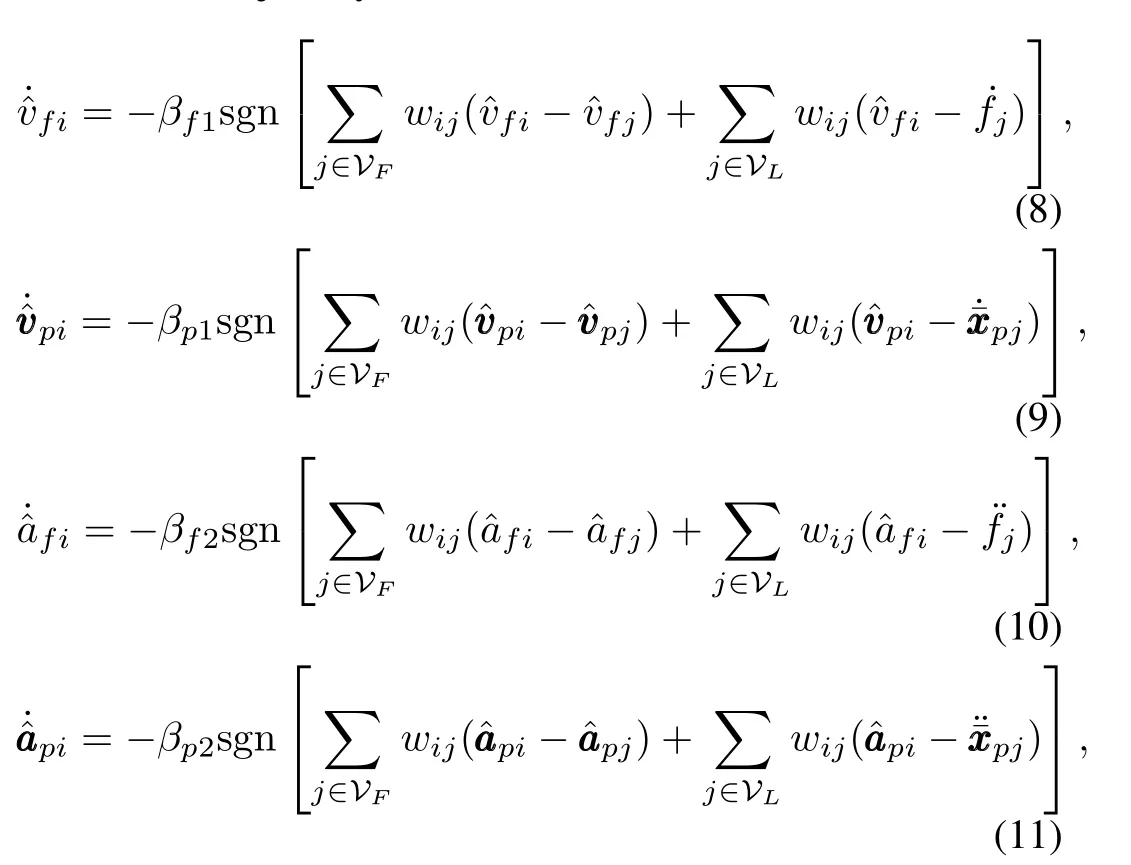
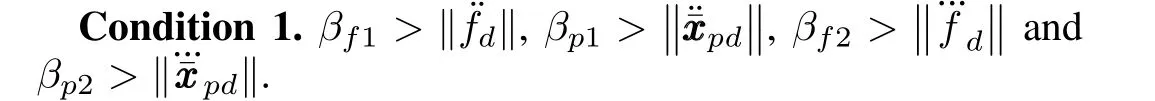

Then,fori∈VF,we design the estimated joint-space reference velocity based on the estimated desired trajectory
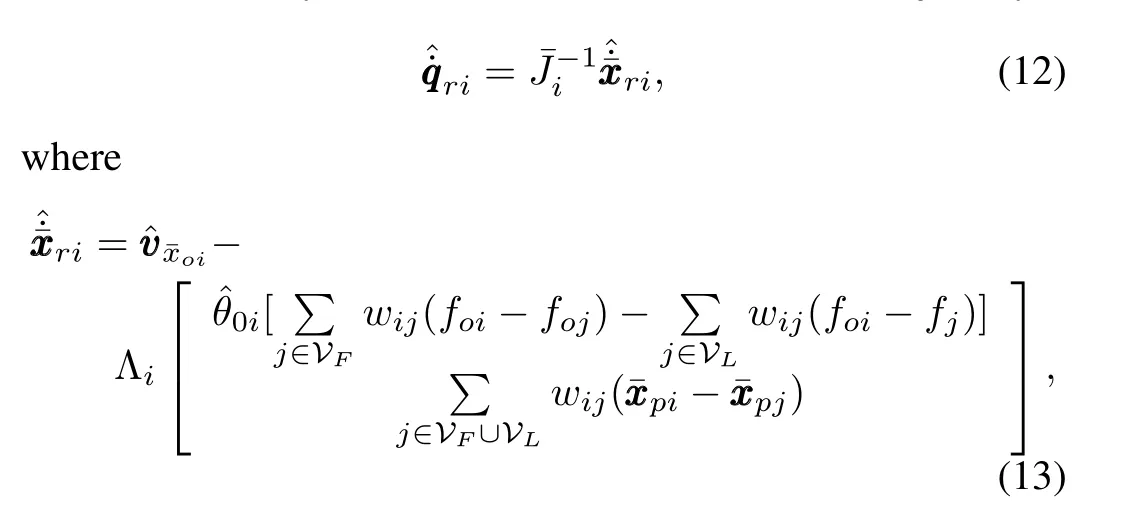


Now,we proceed to analyze quality of the kinematic loop.The following lemmas will be adopted.


Denote the estimated joint-space sliding mode vector and the estimated task-space sliding vector respectively as

Obviously,from(3),(12),(17)and(18),we have

Substituting(13)and(16)into(15),we get

Let Δfoi=foi-fdi.Then,(20)can be rewritten as

Quality of the kinematic loop is given in the following theorem.




The Lyapunov functionVfiis then constructed for the observer dynamics as

DifferentiatingVfiwith respect to time and substituting(15)and(22)into it,we obtain


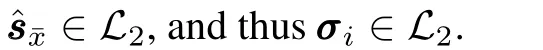

Remark 1.Our construction of the decentralized force observer(16)not only removes the requirement for the measurements of force derivatives,but also provides a simple and direct solution to the force synchronization problem with environment uncertainties under directed graphs containing a spanning tree.In fact,if we do not introduce(16),the reference task-space velocity is still constructed as(13)withfoireplaced byfi,i.e.,
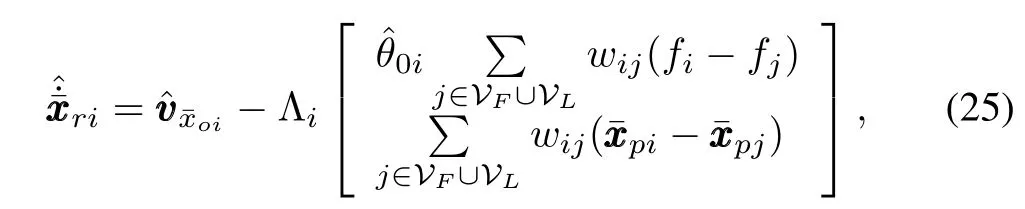
Substituting(25)into(18),we get the closed-loop kinematic equation
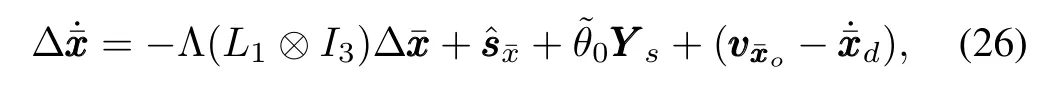
B.Dynamic Loop Design
In this part,we will devise the control lawτifor(3)such that not only Condition 2 for the kinematic loop design is satisfied,but the velocity tracking errors of all the robotic followers are also driven to zero,i.e.,

Now,it is time for us to design the adaptive control law.On the basis of(12)and(13),we define the estimated task-space reference acceleration as
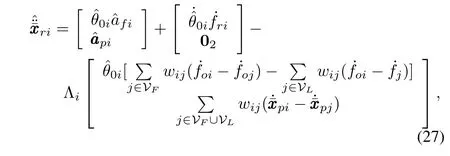
the estimated joint-space reference acceleration as
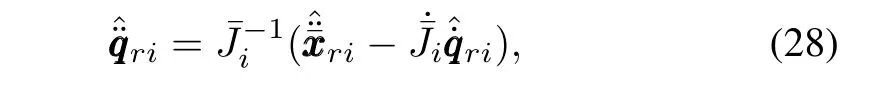
and the dynamic regressor matrixYdias
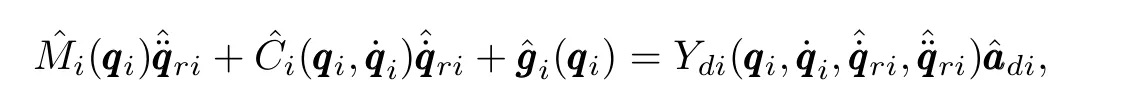
Then,we propose the following adaptive control law
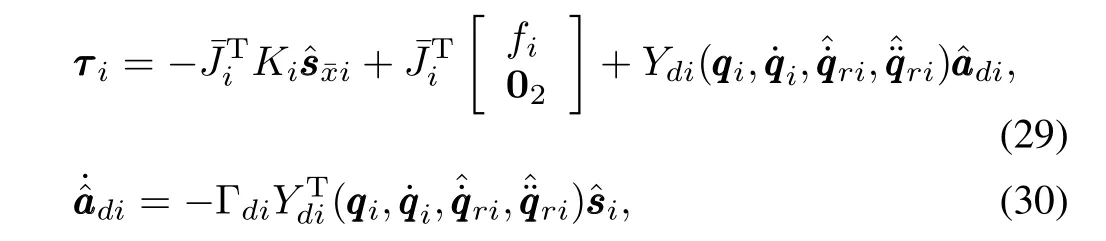
whereKiand Γdiare the adjustable positive definite matrices.
Now,for the overall system constituted by kinematic loop and dynamic loop,we present the following theorem.
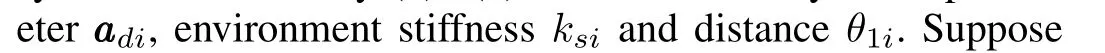
Proof.We first substitute(29)into(4)to get the closed loop dynamics
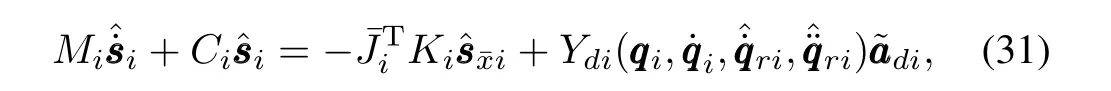
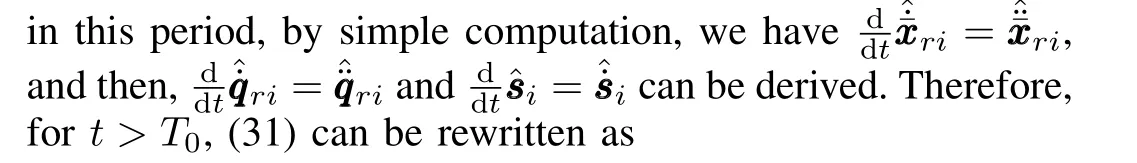

Let us take the Lyapunov-like function as
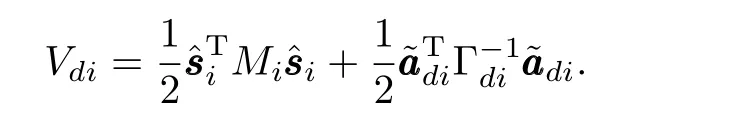
We differentiateVdiwith respect to time and substitute(30)into it.Due to the skew symmetry property of˙Mi-2Ci,we have




IV.SIMULATION
In this section,we use six two-link planar robotic manipulators to validate our control algorithm.For theith manipulator,physical parameters of the two links are selected as



Fig.2.Interaction graph of the agents.
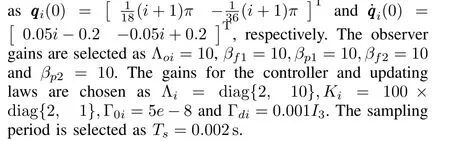
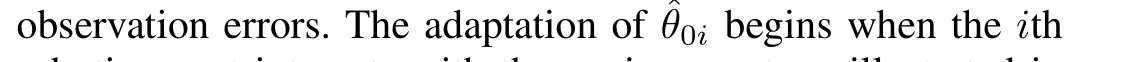

Fig.3.Force tracking errors of the agents.
V.CONCLUSION
In this paper,we consider force/position consensus tracking of multiple robotic manipulators under directed graphs,where the end-effectors of the robots are in contact with flat compliant surfaces with uncertain stiffness and distance.We propose a distributed adaptive hybrid controller to realize both force and task-space position tracking to the convex hull spanned by the leaders.A novel decentralized force observer is constructed to achieve consensus tracking in the force direction with environment uncertainties,which also helps to get rid of the reliance on the measurements of force derivatives.A decentralized stiffness estimator is constructed to estimate environment parameters online.Our scheme removes the requirement for the estimation of surface distance,and offers a simple and direct solution to force synchronization problem in a cascaded framework.Simulations are also performed to examine effectiveness of the proposed strategy.Our future work will focus on investigating the feasibility of extending our strategy to the case when the surface-orientation uncertainties as well as the robotic kinematic and dynamic uncertainties are involved.
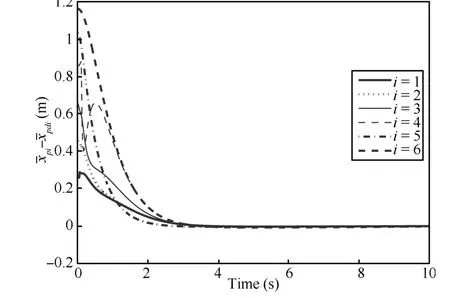
Fig.4.Position tracking errors of the agents.

Fig.5.Observation errors of the force observers.

Fig.6.The updating process ofˆθ0i.
[1]Jones C V,Mataric M J.Behavior-based coordination in multi-robot systems.Autonomous Mobile Robots:Sensing,Control,Decision-Making and Applications.United States:Marcel Dekker,Inc.,2005
[2]Bullo F,Cortes J,Martinez S.Distributed Control of Robotic Networks.Princeton:Princeton University Press,2009
[3]Ren W.Distributed leaderless consensus algorithms for networked Euler-Lagrange systems.International Journal of Control,2009,82(11):2137-2149
[4]Chopra N,Spong M W,Lozano R.Synchronization of bilateral teleop-erators with time delay.Automatica,2008,44(8):2142-2148
[5]Sun D,Shao X Y,Feng G.A model-free cross-coupled control for position synchronization of multi-axis motions:theory and experiments.IEEE Transactions on Control Systems and Technology,2007,15(2):306-314
[6]Nuno E,Ortega R,Basanez L,Hill D.Synchronization of networks of nonidentical Euler-Lagrange systems with uncertain parameters and communication delays.IEEE Transactions on Automatic Control,2011,56(4):935-941
[7]Cao Y,Ren W,Meng Z.Decentralized finite-time sliding mode estimators and their applications in decentralized finite-time formation tracking.Systems&Control Letters,2010,59(9):522-529
[8]Mei J,Ren W,Ma G.Distributed containment control for Lagrangian networks with parametric uncertainties under a directed graph.Automatica,2012,48(4):653-659
[9]Wang H.Task-space synchronization of networked robotic systems with uncertain kinematics and dynamics.IEEE Transactions on Automatic Control,to be published
[10]Wang L J,Meng B,Wang H T.Adaptive task-space synchronisation of networked robotic agents without task-space velocity measurements.International Journal of Control,DOI:10.1080/00207179.2013.835173
[11]Careli R,Kelly R,Ortega R.Adaptive force control of robot manipulators.International Journal of Control,1990,52(1):37-54
[12]Chiaverini S,Siciliano B,Villani L.Force and position tracking:parallel control with stiffness adaptation.IEEE Control Systems Magazine,1998,18(1):37-54
[13]Villani L,de Wit C C,Brogliato B.An exponentially stable adaptive control for force and position tracking of robot manipulators.IEEE Transactions on Automatic Control,1999,44(4):798-802
[14]Doulgeri Z,Karayiannidis Y.Force/position tracking of a robot in compliant contact with unknown stiffness and surface kinematics.In:Proceedings of IEEE International Conference on Robotics and Automation.Roma,Italy:IEEE,2007.4190-4195
[15]Li Z,Li J,Kang Y.Adaptive robust coordinated control of multiple mobile manipulators interacting with rigid environment.Automatica,2010,46(12):2028-2034
[16]Cortesao R,Coutinho F.Environment stiffness estimation with multiple observers.In:Proceedings of IEEE 35th Annual Conference on Industrial Electronics.Porto,Portugal:IEEE,2009.1537-1542
[17]Craig J J.Introduction to Robotics:Mechanics and Control.Upper Saddle River,NJ:Prentice Hall,2005.135-139
[18]Kelly R,Santibanez V,Loria A.Control of Robot Manipulators in Joint Space.London:Springer,2005.113-116
[19]Lozano R,Brogliato B,Egeland O,Maschke B.Dissipative Systems Analysis and Control.London:Springer-Verlag,2000.182-186
[20]Slotine J J E,Li W.Applied Nonlinear Control.Englewood Cliffs,NJ:Prentice Hall,1991.397-409
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Modeling and Hybrid Optimization of Batching Planning System for steel making-continuous Casting Process
- Timesharing-tracking Framework for Decentralized Reinforcement Learning in Fully Cooperative Multi-agent System
- Containment Control of General Linear Multi-agent Systems with Multiple Dynamic Leaders:a Fast Sliding Mode Based Approach
- Bilateral Teleoperation of Multiple Agents with Formation Control
- Distributed Sparse Signal Estimation in Sensor Networks UsingH∞HH-Consensus Filtering
- Adaptive Nonsingular Terminal Sliding Mode Control Design for Near Space Hypersonic Vehicles
