Formation Control for Nonlinear Multi-agent Systems with Linear Extended State Observer

Wen Qin Zhongxin Liu Zengqiang Chen

I.INTRODUCTION

RECENTLY,distributive cooperative control of multi-agent systems,including unmanned underwater vehicles and multi-robot systems,has been a hot research topic in many if elds,such as formation control[1-3],congestion control in communication systems, flocking[4,5]and distributed sensor networks[6].

As a kind of consensus-associated problems[7-10],formation control of multi-agent systems has been primarily investigated in many domains,such as unmanned air vehicles,cooperative transportation and surveillance.Compared with consensus issue,which requires the states of all agents to reach an agreement,the main objective of formation control is to design appropriate protocols that can make the agents achieve consensus of their states as well as preserve a desired geometrical shape with or without a group reference.There are many control methods raised to achieve the control targets,for instance,the leader-following approach[11-13],the behaviour based method[14-16],and the virtual architecture approach[17,18].

Most existing work of formation control for multi-agent systems focuses on local rules using distributed sensing and

Wen Qin and Zhongxin Liu are with the College of Computer and Control Engineering,Nankai University,Tianjin 300071,China,and also with the Tianjin Key Laboratory of Intelligent Robotics,Nankai University,Tianjin 300071,China(e-mail:qinwen.wts@163.com;lzhx@nankai.edu.cn).

Zengqiang Chen is with the College of Computer and Control Engineering,Nankai University,Tianjin 300071,China,with the Tianjin Key Laboratory of Intelligent Robotics,Nankai University,Tianjin 300071,China,and also with the College of Science,Civil Aviation University of China,Tianjin 300300,China(e-mail:chenzq@nankai.edu.cn).controlling.In practice,some information of the agents in a multi-agent system,such as velocity,may not be obtained.For example,the agent may not be equipped with velocity sensors or the velocity measurement is not precise.Thus,the design of controller based on observers becomes a main trend in the research of multi-agent systems.Hong et al.[19,20]studied the leader-follower consensus problem for multi-agent systems with an unknown velocity of variable leader,in which certain neighbour-based rules including distributed controller algorithm and observers were developed.In addition,many physical models in reality are nonlinear and have many uncertain terms.Several types of disturbance evaluating techniques are unknown input observer[21,22],perturbation observer[23],disturbance observer[24,25],and extended state observer(ESO)[26-28].Different from other observers,ESO is designed distinctively to evaluate both extrinsic disturbance and inner uncertainty of the system itself.The total uncertain part is regarded as an augmented state which can be estimated via observer.ESO,working as an estimator,plays a key role in the active disturbance rejection control.Active disturbance rejection control(ADRC)was put forward based on ESO by Han in 1995,which was designed to estimate the total uncertainties on-line using ESO[26].Besides,the nonlinear extended state observer could be simplified into a linear ADRC(LADRC)which is mainly discussed in this paper.

Motivated by the aforementioned statements,the formation control for a class of nonlinear multi-agent systems with a virtual leader to be tracked by followers is investigated in this paper.The followers respond to the virtual leader as they respond to their neighbours.We emphasize that there is no real leader among the followers.The introduction of a virtual leader increases robustness of the group in case of any single vehicle′s failure.A distributed linear extended state observer(LESO)for second order multi-agent systems is proposed in the circumstance that velocities of an agent′s neighbors cannot be measured.Furthermore,some local laws based on LESO are devised to track the active virtual leader,and the followers can shape the desired group formation by switching topology at the same time.The asymptotic stability for closed systems is guaranteed by a given model of the nonlinear couplings and the boundary of tracking error is obtained without a specific model of the plant.

The organization of this article is as follows.In Section II,some preliminary knowledge is outlined.In Section III,by designing a distributed control based on LESO,some sufficient conditions are proposed to ensure that the agents achieve the desired configuration with given or unknown nonlinear functions under the switching topology situation.Illustrative examples are presented to show validity of the theoretical results in Section IV,and the concluding statements are given in Section V.

II.PRELIMINARIES AND PROBLEM FORMULATION

A.Notations

We first review some knowledge of graph theory and matrix analysis that we will use in the following sections.Consider a system containing one virtual leader andnagent-followers depicted by graph¯G.Graph¯Gincludesnfollowers,which are related to graphG,and a virtual leader,which sends information to some follower agents via directed edges.The graphG(V,E,A)without self-loops is composed of the node setV={v1,···,vn},the edge setE∈V×V,whose element is denoted byeij=(vi,vj)(i/=j),and the adjacency matrixA=[aij](i,j=1,2,···,n),whereaij＞0 if(vi,vj)∈E,aij=0 if(vi,vj)/∈Eandaii=0.The Laplacian matrix associated with the graph is expressed asL=D-A,whereD=[dij]is the diagonal degree matrix,with diagonal elementsdii=Pnj=1aij.The set of neighbours of agentiis denoted byNi(t)={vj∈V:eij=(vi,vj)∈E}at timet.B=diag{b1,···,bn}is a diagonal matrix with the elements denoting the connection between the virtual leader and the follower agents,wherebi＞0 if the virtual leader is a neighbour of agenti,and otherwise,bi=0.

The maximal connected subgraphG1induced fromG,is named as a component ofG.We call graph¯Gconnected graph if at least one agent of each component ofGis linked to the virtual leader via a directed edge.

In addition,to describe the variation of the relationship between agents,we define a piecewise-constant switching signalσ:[0,∞)→Π ={1,2,···,N}.p=σ(t)∈Π switches in different time intervals[tj,tj+1),wheretj+1-tj≤τ1(τ1＞0,j=0,1,···).The time intervals are bounded,nonoverlaying and continuous.Therefore,Ni(t),aij(i,j=1,2,···,n),LpandBprelated with the switching interconnection graph¯Gpare time-varying(p∈Π).

B.Linear Extended State Observer for Multi-agent Systems with Total Uncertainty

We consider a team ofnagents moving with a virtual leader operating in the same workspace.

The virtual leader is described as

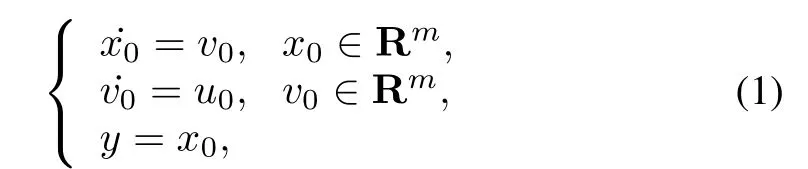
wherex0,v0∈Rmare the virtual leader′s position and velocity state,respectively.Inputu0is known to all agents.The moving virtual leader we set is a known group reference to some followers representing a common interest of all the agents.

The following second-order system ofnagents is modeled as

wherexi,vi∈Rmare the position and velocity states of agenti(i=1,2,···,n),respectively.f(xi,vi,ω)∈Rmis a nonlinear function to portray the inner dynamics of agenti,whereωis exterior disturbance.ADRC is developed to deal with this problem.Presuming thatfis differentiable,and setting

Considering thatfis an extended state in model(3),LESO for(3)is designed and the evaluation error of LESO is revealed in the next part.

Remark 1.In system(3),f(xi,vi,ω)is the total uncertainty function which includes internal uncertain dynamics and external disturbance,and thus it is not easy to obtain the exact model off(xi,vi,ω).In the following section,the total uncertain partfwill be seen as an augmented state,and can be estimated using the designed LESO.

C.Convergence of LESO

1)Convergence of LESO with the given model of the plant:We first consider the case that the model offis known.

The following decentralized LESO for(3)is proposed with the given functionh,

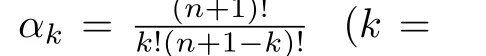
which makesω0turn out to be the only adjustable parameter of LESO.

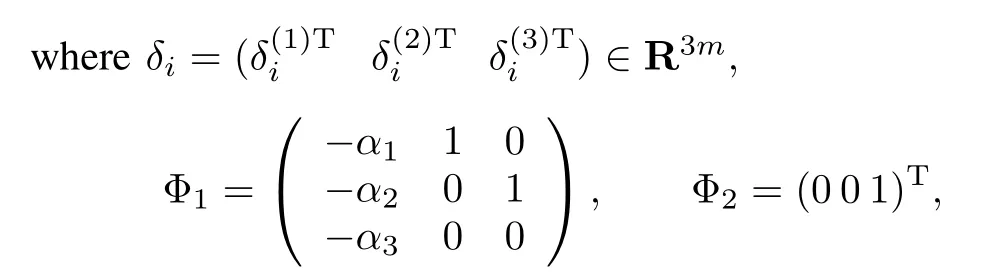
where Φ1is Hurwitz according to the selection ofαi(i=1,2,3).

Considering the above analysis,the following lemma quoted from[29]will be useful.

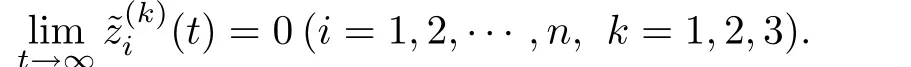
Remark 2.In this subsection,LESO for system(3)is presented,where the model offis completely known.Consequently,the derivative of functionfis added in LESO(4).

Remark 3.Compared with the nonlinear extended state observer in[27]and other kinds of observers,ω0turns out to be the only adjustable parameter of LESO according to(5).In addition,parameterω0can be determined byω0＞1+‖PΦ2c′‖2,wherePis a positive definite matrix satisfying ΦT1P+PΦ1=-I,c′is the Lipschitz constant related toh[29].

2)Convergence of LESO with the unknown function model:In this part,we will study the case that the nonlinear function including uncertainty,i.e.,the dynamics of plantfis largely unknown.Different from(4),LESO in(4)now takes the form of

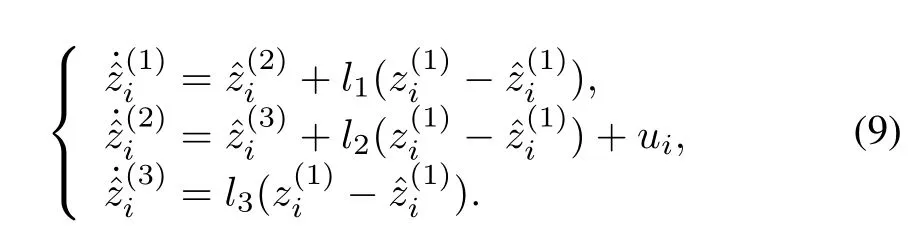
The observer estimation error in(7)becomes

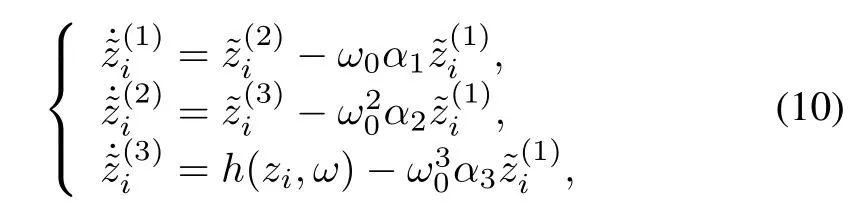
and(8)can be expressed as

Similar to the above analysis,we can get Lemma 2.

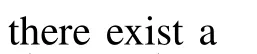
Remark 4.Different from the case that the model of plant is given in Section II-C-1,LESO(9)for system(3)is presented in the face of unknown nonlinear function in Section II-C-2.Therefore,the derivative of functionfdoes not appear in LESO(9).

III.MAIN RESULTS

A.ADRC for Multi-agent Systems with Given Model of Plant

Our control goal here is to coordinate all the agents to achieve the prescribed spatial pattern,and to maintain the consistent pace of the virtual leader with the velocity of all agents converging tov0,i.e.,z(1)i-x0→ci,z(2)i →v0ast→∞,whereci(i=1,2,···,n)is the expected constant relative position vector between agentiand the virtual leader.

With the assurance that our LESO is convergent,the LESO-based local law will have the form of fori=1,2,···,n,with constantsk1,k2＞0 to be determined,along with LESO(4).

The lemmas used in the proofs of the following theorems are given hare.

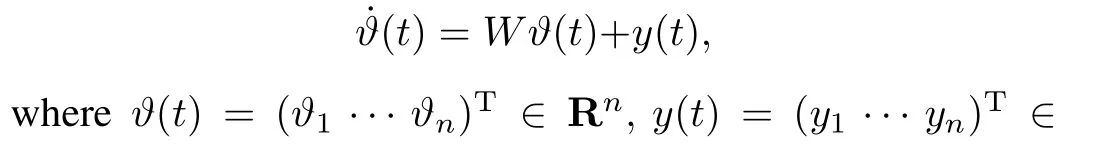
ConsiderRn,andWis ann×nmatrix.

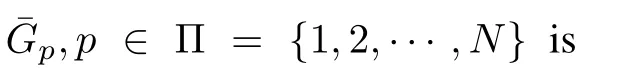
Considering system(3)and LESO(4),we have Theorem 1.

Theorem 1.Assuming thath(zi,ω)is globally Lipschitz regarding tozi,if the entire graph¯Gp(p∈Π={1,2,···,N})is connected in each time interval[tk,tk+1),there exist constantsω0＞0 andk1,k2＞0,such that controller(12)with LESO(4)together yields

namely,the agents can attain and preserve pre-described formation,and reach velocity consensus under arbitrary switching rule among the possible topologies.

Proof.e1ande2are set as

From Lemma 4,we getLp+Bp(p∈Π)is positive definite,thenk1,k2can be selected such that Ωeis Hurwitz.

In the above theorem,the connected condition in each time interval[tk,tk+1)(k=0,1,···)is somehow strong.Then we will discuss the case with jointly connected condition.

Assume that in each interval[tk,tk+1)(k=0,1,···)there is a sequence of bounded,nonoverlapping subintervals

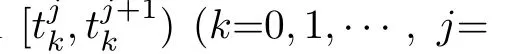
Assumption1.The graphs over each time interval[tk,tk+1)(k=0,1,···)are jointly connected.

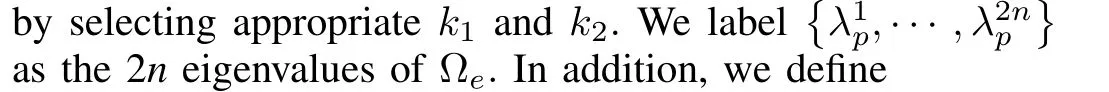
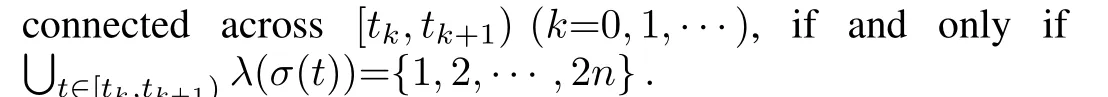
With the previous discussion,we will give the following theorem.

Theorem 2.With the assumption thath(zi,ω)is globally Lipschitz regarding tozi,if the interaction graph satisfies Assumption 1,then there exist constantsω0＞0 andk1,k2＞0,such that controller(12)with LESO(4)together yields

namely,the agents can attain and preserve desired formation,and reach velocity consensus.

Next,we will prove Theorem 2.

Proof.Consider the Lyapunov functionV(t)=eT(t)e(t)based on(14).

1)We will first show that˙V≤0.Without losing generality,we assume that thepth graph is active at timet,then

Since ΩeT+Ωeis symmetric and we label its 2nnonpositive eigenvalues asµ(p)={µ1p,µ2p,···,µ2np},there exists an orthogonal matrixWpsuch that

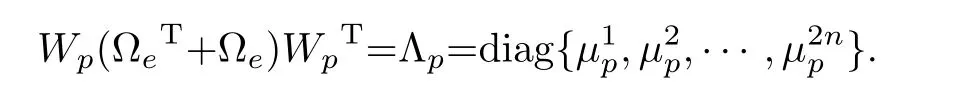
Then we can obtain by translation¯e=Wpe,

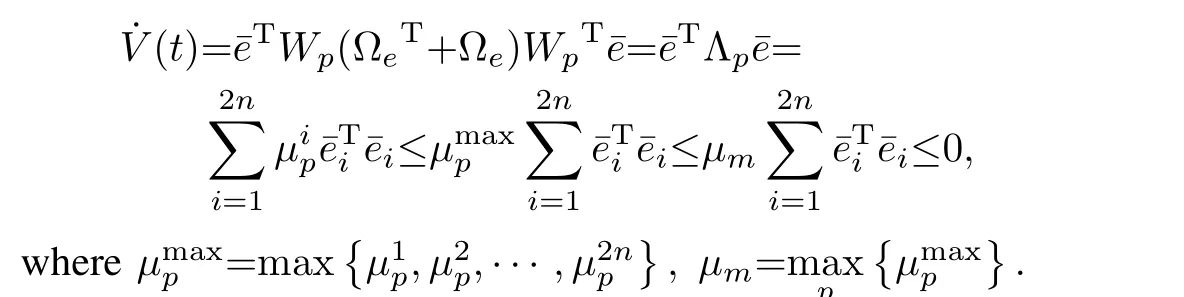
For arbitraryε＞0,there exists a constantKsuch that∀k≥K,

Thus,for nonnegative integerk＞K,we have

From 1)and 2),the proof is completed. □

Remark 6.It should be noted that the formation control problem in Theorem 1 is studied with the condition that the graphs in each interval[tk,tk+1)are connected,which is somehow strong,while switching between all the possible topologies is random without restriction.However,in Theorem 2,we relax the condition to jointly connected graphs across[tk,tk+1),which imposes certain requirements on designing the rule of switching among the possible topologies.

B.ADRC for Multi-agent Systems with Function Model Mostly Unknown

In the following,we investigate the problem without detailed model of nonlinear function by LESO(9).

Theorem 3.With the assumption thath(zi,w)is bounded,if the entire graph¯Gp(p∈Π={1,2,···,N})is connected in each time interval[tk,tk+1),there exist constantsξi＞0,ω0＞0 andk1,k2＞0 such that controller(12)with LESO(9)together yields

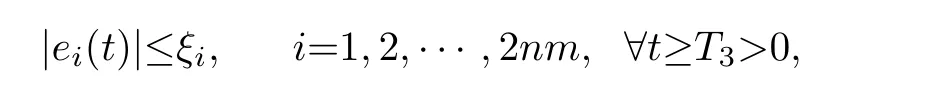
namely,the tracking error is bounded.

Proof.Solving(14),we get

From(14)and Lemma 2,we can get for anyt≥T1,

is theith element ofϕ(t),and

Since Ωeis Hurwitz,we have

fort≥T2,i,j=1,2,···,2nm.LetT3=max{T1,T2}.It follows that

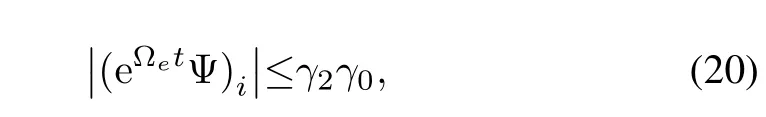
fort≥T3,i=1,2,···,2nm,and

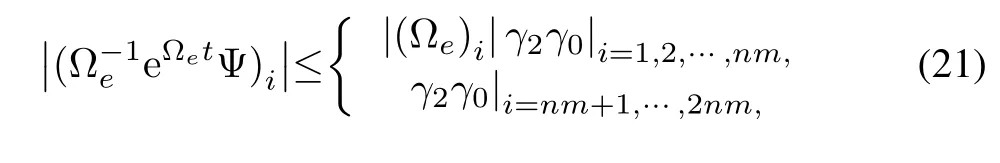
fort≥T3.According to(17),(18)and(21),we have

for allt≥T3.Letesum(0)=|e1(0)|+|e2(0)|+···+|e2nm(0)|.The following inequality is obtained

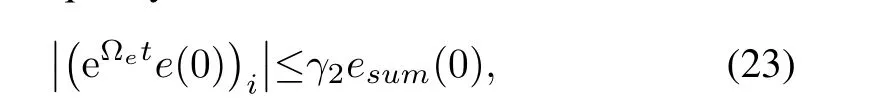
fort≥T3,i=1,2,···,2nm.From(15),it follows that

According to(15),(22)～(24),we have

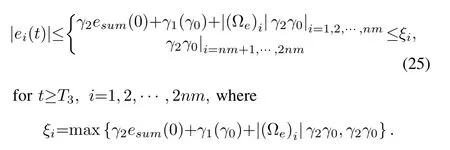
This completes the proof. □

Remark 7.In Section III-A,ADRC based on LESO(4)is put forward for the exact model of the plant which is completely known.Differently,in Section III-B,ADRC based on LESO(9)is designed when the nonlinear uncertain function model is mostly unknown.

Remark 8.Since the strong estimation and compensation ability,ADRC based on LESO is widely applied due to its marvellous merits,especially in engineering projects.

1)In practice,the uncertainties are usually derived from two sources,internal uncertainty(including parameter and structure uncertainty)and external disturbance.There are many control methods aiming at these two issues,such as proportion integration differentiation(PID),robust control and disturbance observer.However,owning to less dependence on system model,as the estimation mechanism in ADRC,LESO is used to not only estimate all the system states but also evaluate the total uncertainty online.

2)According to real-time estimated values as stated in 1)above,ADRC can compensate the internal and external disturbance actively.

In sum,ADRC method,which depends on less information of system model,can estimate and offset the total uncertainty coming from internal and external disturbance.Combining with the distributed control idea,it has the advantage of strong robustness against many kinds of uncertainty.

IV.NUMERICAL SIMULATIONS

In the rest of the paper,numerical simulations are given to verify effectiveness of the protocols proposed above.

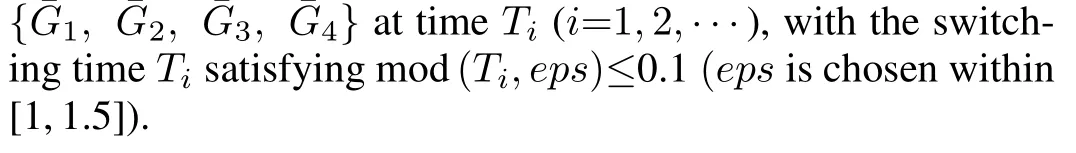
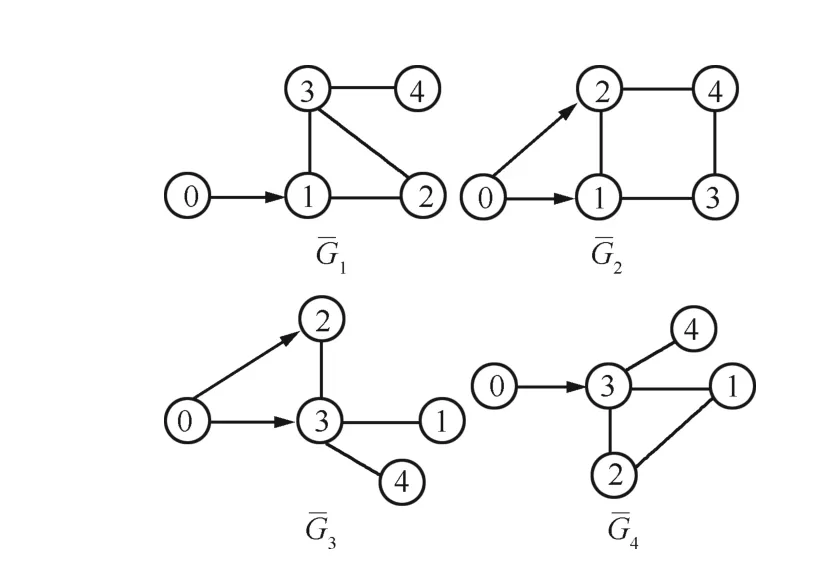
Fig.1. Four possible network topologies associated with graphs¯Gp(p=1,2,3,4).

Case 1(a).The multi-agent system with the given plant model satisfies the conditions of Theorem 1 and the topologies are shown in Fig.1.Here,

We choosec1=(-6-3)T,c2=(6-3)T,c3=(6 3)T,c4=(-6 3)T,ω0=8 andk1=k2=1.The original positions are chosen within[-5,5]at random,the initial velocities arev1=v2=v3=v4=(0.1 0.1)T.It can be easily verified that the conditions of Theorem 1 are satisfied.The position errors and the velocity errors of simulation results are shown in Figs.2～6,respectively.We can see that the followers have achieved the desired formation and velocity consensus has been reached,where the final positions of the followers and the virtual leader are marked by ‘◊’and ‘o’,respectively,in Fig.2.Fig.2 shows that the followers asymptotically form the pre-described formation and reach velocity consensus.

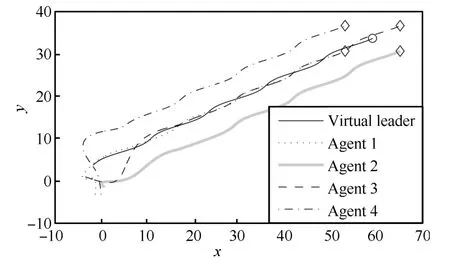
Fig.2. Trajectories of agents in Case 1(a).

Fig.3 shows that the relative distances between the virtual leader and followeri(i=1,2,3,4)are

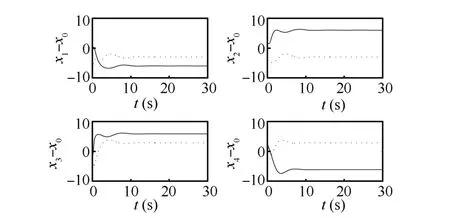
Fig.3.Trajectories of relative distance between the virtual leader and follower i(i=1,2,3,4)in Case 1(a).

Fig.4 Trajectories of position errors e1in Case 1(a).

Fig.5. Trajectories of velocity errors e2in Case 1(a).

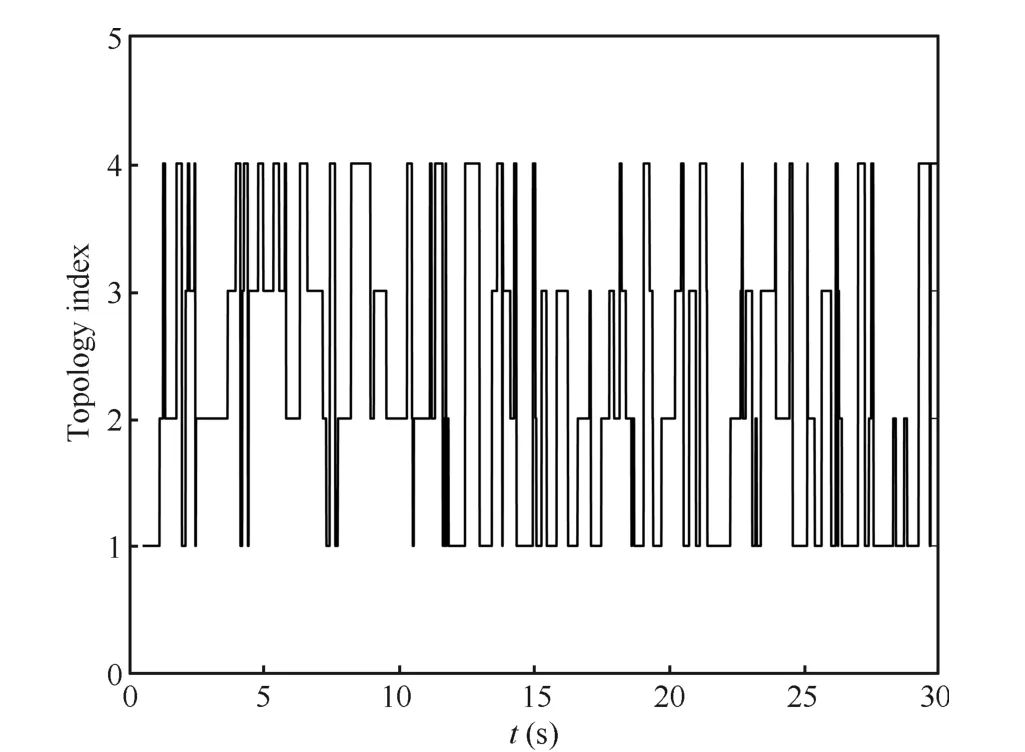
Fig.6.Random switching among 4 possible topologies in Case 1(a).

Case 1(b).The multi-agent system with the given plant model satisfies the conditions of Theorem 2,and we use the same parameters as in Case 1(a).Four possible topologies of the multi-agent system are shown in Fig.7.

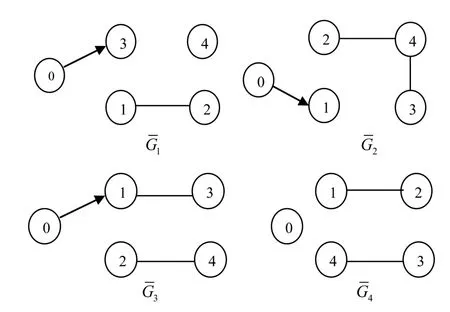
Fig.7.Four possible network topologies associated with graphs

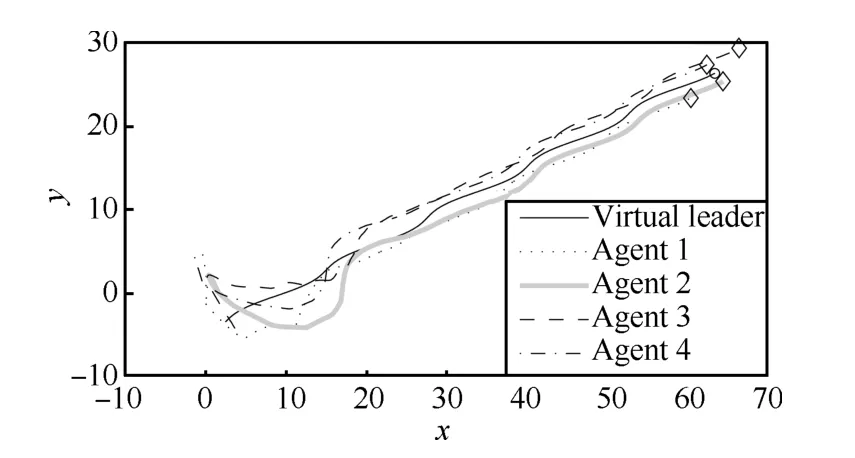
Fig.8. Trajectories of agents in Case 1(b).

Fig.9. Trajectories of relative distance between the virtual leader and follower i(i=1,2,3,4)in Case 1(b).

Fig.10. Trajectories of position errors e1in Case 1(b).

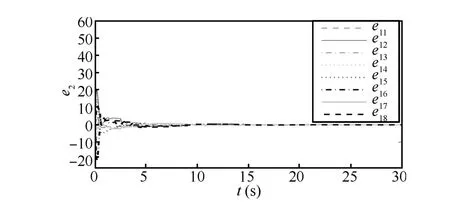
Fig.11. Trajectories of velocity errors e2in Case 1(b).

Fig.12. Designed switching signal among 4 possible topologies in Case 1(b).

Case 2(a).The formation control for multi-agent system with plant dynamics largely unknown is studied in this case where the observer bandwidthω0=8.

We use the same parameters as Case1 and the topologies used are shown in Fig.1.Then we can choosec1=(0-3)T,c2=(8 0)T,c3=(0 3)T,c4=(-8 0)T,ω0=8,andk1=k2=1.Thus it is easy to show that the conditions of Theorem 2 are satisfied.The simulation-based results presented in Figs.13～16 show that the tracking error is bounded with LESO(9).

Case 2(b).The formation control for multi-agent system with plant dynamics largely unknown is investigated in this part where the observer bandwidthω0=50.

The topologies used are shown in Fig.1.We choosec1=(0-8)T,c2=(3 0)T,c3=(0 8)T,c4=(-3 0)T,andω0=50,then we can see that the follower agents can form the desired formation and the tracking error will be decreased in Figs.17～20.

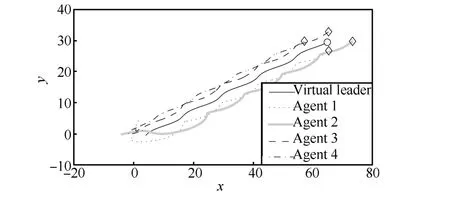
Fig.13 Trajectories of agents in Case 2(a).

Fig.14.Trajectories of relative distance between the virtual leader and follower i(i=1,2,3,4)in Case 2(a).

Fig.15. Trajectories of position errors e1in Case 2(a).

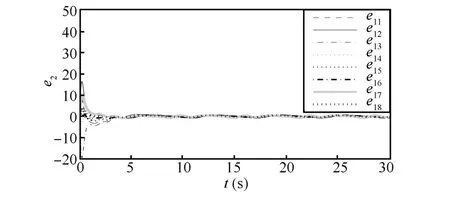
Fig.16.Trajectories of velocity errors e2in Case 2(a).

Fig.17. Trajectories of agents with ω0=50 in Case 2(b).

Fig.18.Trajectories of relative distance between the virtual leader and follower i(i=1,2,3,4)with ω0=50 in Case 2(b).

Comparison between Figs.15,16 and Figs.19,20 demonstrates that if the parameter is selected appropriately,the tracking errors will be decreased.

V.CONCLUSION

The paper investigated formation control for a class of nonlinear multi-agent systems with a virtual leader.Based on LESO,an active disturbance rejection control is developed that can make the followers achieve and preserve the desired formation under two situations.The sufficient condition is that the graph is connected with the given nonlinear function,which is then relaxed to the case that the graphs are jointly connected.However,in the face of large model uncertainties,the tracking errors are shown to be bounded.For some condition restrictions,it is somehow difficult to apply the jointly connected condition to the model with large uncertainty,thus further research will be considered in future.Finally,simulation examples are provided.

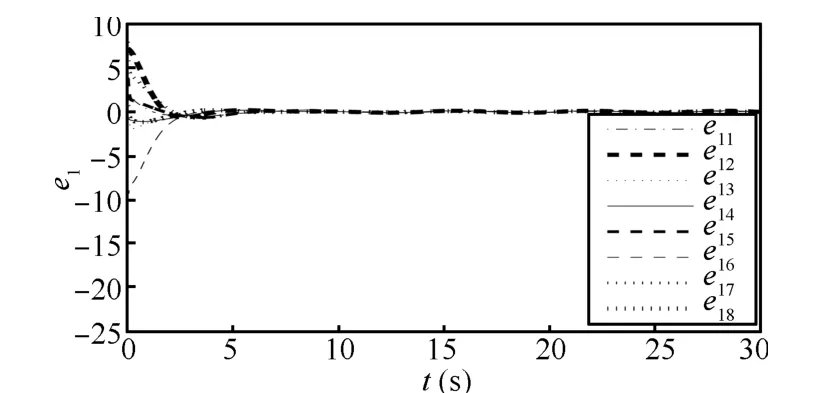
Fig.19. Trajectories of position errors e1with ω0=50 in Case 2(b).

Fig.20. Trajectories of velocity errors e2with ω0=50 in Case 2(b).

ACKNOWLEDGEMENT

The authors acknowledge Mingwei Sun for the valuable suggestions on the theory and application of active disturbance rejection control(ADRC)and the anonymous reviewers.

[1]Zheng Jun,Yan Wen-Jun.A distributed formation control algorithm and stability analysis.Acta Automatica Sinica,2008,34(9):1107-1113(in Chinese)

[2]Xiao F,Wang L,Chen J,Gao Y P.Finite-time formation control for multi-agent systems.Automatica,2009,45(11):2605-2611

[3]Chen F,Chen Z Q,Liu Z X,Xiang L Y,Yuan Z Z.Decentralized formation control of mobile agents:a unified framework.Physica A:Statistical Mechanics and its Applications,2008,387(19-20):4917-4926

[4]Wen G H,Duan Z S,Li Z K,Chen G R.Flocking of multi-agent dynamical systems with intermittent nonlinear velocity measurements.International Journal of Robust and Nonlinear Control,2012,22(16):1790-1805

[5]Chen Z Y,Zhang H T.Analysis of joint connectivity condition for multi-agents with boundary constraints.IEEE Transactions on Cybernetics,2013,43(2):437-444

[6]Tu Zhi-Liang,Wang Qiang,Shen Yi.A distributed simultaneous optimization algorithm for tracking and monitoring of moving target in mobile sensor networks.Acta Automatica Sinica,2012,38(3):452-461(in Chinese)

[7]Yan J,Guan X P,Luo X Y,Yang X.Consensus and trajectory planning with input constraints for multi-agent systems.Acta Automatica Sinica,2012,38(7):1074-1082

[8]Su Y F,Huang J.Cooperative output regulation of linear multi-agent systems by output feedback.Systems and Control Letters,2012,61(12):1248-1253

[9]Li Z K,Liu X D,Ren W,Xie L H.Distributed tracking control for linear multi-agent systems with a leader of bounded unknown input.IEEE Transactions on Automatic Control,2013,58(2):518-523

[10]Ren W.Consensus based formation control strategies for multi-vehicle systems.In:Proceedings of the American Control Conference.Minneapolis,MN:IEEE,2006.4237-4242

[11]Dong Y,Huang J.Leader-following rendezvous with connectivity preservation of a class of multi-agent systems.In:Proceedings of the 2012 31st Chinese Control Conference(CCC).Hefei,China:IEEE,2012.6477-6482

[12]Qin W,Liu Z X,Chen Z Q.Impulsive formation control algorithms for leader-following second-order nonlinear multi-agent systems.In:Proceedings of the 13th IFAC Symposium on Large Scale Complex Systems:Theory and Applications.Shanghai,China:IFAC,2013.172-177

[13]Wang J L,Wu H N.Leader-following formation control of multi-agent systems under fixed and switching topologies.International Journal of Control,2012,85(6):695-705

[14]Arkin R C.Behavior-Based Robotics.Cambridge,MA:MIT Press,1998

[15]Balch T,Arkin R C.Behavior-based formation control for multirobot teams.IEEE Transactions on Robotics and Automation,1998,14(6):926-939

[16]Lumelsky V J,Harinarayan K R.Decentralized motion planning for multiple mobile robots:The cocktail party model.Autonomous Robots,1997,4(1):121-135

[17]Lewis M A,Tan K H.High precision formation control of mobile robots using virtual structures.Autonomous Robots,1997,4(4):387-403

[18]Hernandez-Martinez E G,Aranda Bricaire E.Non-collision conditions in multi-agent virtual leader-based formation control.International Journal of Advanced Robotic Systems,2012,9:100

[19]Hong Y G,Hu J P,Gao L X.Tracking control for multi-agent consensus with an active leader and variable topology.Robotics and Autonomous Systems,2006,42(7):1177-1182

[20]Hong Y,Chen G R,Bushnell L.Distributed observers design for leader following control of multi-agent.Automatica,2008,44(3):846-850

[21]Basile G,Marro G.On the observability of linear,time-invariant systems with unknown inputs.Journal of Optimization Theory and Applications,1969,2(6):410-415

[22]Chen J,Patton R J,Zhang H Y.Design of unknown input observers and robust fault detection filters.International Journal of Control,1995,63(1):85-105

[23]Kwon S,Chung W K.Combined synthesis of state estimator and perturbation observer.ASME Journal of Dynamic Systems,Measurement,and Control,2003,125(1):19-26

[24]Yang H Y,Guo L,Han C.Tracking trajectory of heterogenous multi-agent systems with disturbance observer based control.In:Proceedings of the 2012 10th World Congress on Intelligent Control and Automation(WCICA).Beijing,China:IEEE,2012.2352-2357

[25]Yang H Y,Guo L,Zou H L.Robust consensus of multi-agent systems with time-delays and exogenous disturbances.International Journal of Control,Automation and Systems,2012,10(4):797-805

[26]Han Jing-Qing.A class of extended state observers for uncertain systems.Control and Decision,1995,10(1):85-88(in Chinese)

[27]Gao Z Q,Han Y,Huang Y Q.An alternative paradigm for control system design.Decision and Control,2001.In:Proceedings of the 40th IEEE Conference on Decision and Control.Orlando,FL:IEEE,2001.5:4578-4585

[28]Gao Z Q.Scaling and bandwidth-parameterization based controller tuning.In:Proceedings of the 2003 American Control Conference.Denver,USA:IEEE,2003.6:4989-4996

[29]Zheng Q,Gao L Q,Gao Z Q.On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics.In:Proceedings of the 2007 46th IEEE Conference on Decision and Control.New Orleans,LA:IEEE,2007.3501-3506

[30]Ni W,Cheng D Z.Leader-following consensus of multi-agent systems under fixed and switching topologies.Systems and Control Letters,2010,59(3-4):209-217