一类二阶哈密顿系统的无穷多同宿轨
2014-02-05张申贵
张申贵,李 琰
(1 西北民族大学数学与计算机科学学院,甘肃 兰州,730030;2 兰州市第八中学)
哈密顿系统所描述的运动是运动中最简单的周期运动,天体的周期轨道就对应于非线性哈密顿系统的同宿轨。哈密顿系统周期解和同宿轨一直是数学家和物理学家所关心的重要课题。考虑二阶哈密顿系统
(1)
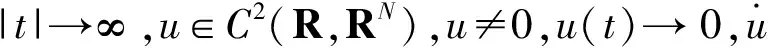
当B≡0时,一些学者开始利用临界点理论对系统(1)的同宿轨进行研究[1~8], 得到了一些同宿轨存在的结果,如次线性条件[1],次二次条件[2],超线性条件[3~5],变号位势[6],渐进线性[7,8]等。
当B不恒等于0时,文献[9]在超线性条件研究了系统(1)同宿轨的存在性。
当B不恒等于0时,具有线性增长非线性项时,本研究将分析系统(1)无穷多同宿轨的存在性。
1 准备知识
记H为H1(R,RN)为Hilbert空间,定义算子J:H→H为Ju,v

λ1≤λ2≤…≤λk≤…,当k→+∞时,λk→+∞。
对应的特征函数{ek}k∈N,即Aek=λkek。记E=E-⊕E0⊕E+, 其中E0为零特征值对应的特征函数组成,E-为负特征值对应的特征函数组成,E+=(E0⊕E-)⊥。
对∀u∈E,有u=u-+u0+u+,其中u-∈E-,u0∈E0,u+∈E+,

假设L(t)满足以下条件:
(L1)存在常数β>1使得meas{t∈R:|t|-βL(t)

在条件(L1)和(L2)之下,空间E紧嵌入Lp(R,RN),p≥1,从而
‖u‖Lp≤C‖u‖
(2)
在E上定义泛函:
则u∈E为φ的临界点等于u是系统(1)的同宿轨[6]。
引理1[7]:设E为无穷维Banach空间,φ∈C1(E,R)为偶泛函且满足(PS)条件,φ(0)=0。若E=E1⊕E2,其中E1为有限维空间。泛函φ满足以下2个条件:
(i)φ在E2中上方有界。



其中,Bρ={x∈E;‖x‖≤ρ},则泛函φ有无穷多个非平凡临界点。
2 主要结果及其证明
2.1 主要结果
定理1设存在常数M1>0,使得
|Wu(t,u)|≤M1(|u|+1)
(3)
2M1C2<1
(4)
对∀(t,u)∈R×RN成立。且
(5)
对∀(t,u)∈R×RN成立。及
(6)
对t∈R一致成立。若W(t,0)≡0,W(t,-u)=W(t,u),则系统(1)有无穷多个同宿轨。
例如令W(t,x)=|x|2+|x|,则非线性项W(t,x)是关于变量x线性增长的,W(t,x)满足定理1中条件,但不满足文献[1~9]中定理的条件。
2.2 结果证明
证明通过验证泛函φ满足引理1的所有条件,则φ有无穷多个临界点,从而系统(1)有无穷多个同宿轨。以下用c表示常数。
第1步 验证泛函φ满足(PS)条件.设{uj}为(PS)序列, 则
|φ(uj)|≤c,φ′(uj)→0,(j→∞)
(7)

由(2)式、(3)式、Hölder不等式,有
(8)
由(7)式、(8)式,有
‖uj‖≥φ′(uj),≥‖‖2-R(Wu(t,uj),)dt≥‖‖2-(M1C2‖uj‖‖‖+M1C‖‖),
由上式推得:
(9)
同理可证:
(10)
反设当j→∞时‖uj‖→∞,即{uj}在E中无界。
由(9)式、(10)式,并注意到2M1C2<1,当n→∞时,故有
(11)
由(11)式,∀ε>0,当1-2M1C2-ε>0,有
(12)
由(9)式、(10)式,有
(13)
由(2)式、(3)式、Hölder不等式、(13)式有
(14)
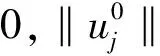
(15)
由(13)式、(14)式、(15)式有

第2步 证明泛函φ在E+中是上方有界的。
由(2)式、(3)式, 对u+∈E+有
注意到2M1C2<1,当‖u‖→∞时,φ(u)→-∞,从而泛函φ满足引理1中条件(i)。
‖u‖∞≤C0‖u‖
(16)

(17)
W(t,u)≥C2|u|2
(18)
对|u|≤M2和t∈R成立。由(16)式、(17)式和(18)式,有

至此, 引理1所有条件均满足,则φ有无穷多个临界点,问题(1)有无穷多个同宿轨。
[1] Yang Minghai,Han Zhiqing.Infinitely many homoclinic solutions for second order Hamiltonian systems with odd nonlinearities[J].Nonlinear Anal,2011,74: 2 635-2 646.
[2] Gui Bao,Han Zhiqing,Yang Minghai.Multiplicity of homoclinic solutions for second order Hamiltonian systems[J].Electronic Journal of Differential Equations,2013,151:1-11.
[3] Yang Jie,ZHang Fubao.Infinitely many homoclinic orbits for the second order Hamiltonian systems with super-quadratic potentials[J].Nonlinear Anal,2009,10:1 417-1 423.
[4] Wan Lili,Tang Chunlei.Existence of homoclinic orbits for second order Hamiltonian systems without (AR) condition[J].Nonlinear Anal,2011,74(16):5 303-5 313.
[5] Lv Yin,Tang Chunlei.Homoclinic orbits for second-order Hamiltonian systems with subquadratic potentials[J].Chaos,Solitons & Fractals,2013,57:137-145.
[6] Deng Xiaoqing,CHeng Gong.Homoclinic orbits for second order discrete Hamiltonian systems with Potential Changing Sign[J].Acta Applican Mathematics,2008,3:301-314.
[7] Ding Yanheng.Existence and multiplicity results for homoclinic solutions to a class of Hamiltonian systems[J].Nonlinear Anal,1995,25(1):1 095-1 113.
[8] Su Y,Feng Z.Homoclinic orbits and periodic solutions for a class of Hamiltonian systems on time scales[J].Journal of Mathematical Analysis and Applications,2014,411(1): 37-62.
[9] Sun Juntao,Nieto J.On homoclinic orbits for a class of damped vibration systems[J].Advances in Difference Equations, 2012,102:10-21.
