一维六方压电准晶材料中双周期裂纹反平面问题

崔江彦, 安震海, 王亚星

(1宁夏大学数学与计算机学院,宁夏 银川，750021;2 银川唐徕回民中学)

准晶是1984年在实验Al-Mn合金中发现的一种固体, 结构与晶体明显不同, 其弹性也不同于晶体。准晶弹性除了普通的位移场和声子场之外, 还存在另一位移场和相位子场。目前准晶材料主要应用于表面改性材料和结构材料增强相, 但是准晶材料在常温环境下呈脆性, 这大大限制了准晶材料的应用, 因此研究其断裂力学行为对材料的制作有着及其重要的理论意义。长期以来, 学者对材料断裂力学的研究都集中在裂纹和夹杂中，自准晶材料被发现以来, 关于准晶各方面问题的研究已经取得了许多重要的成果, 尤其是用复变函数的方法研究准晶材料中一系列微观与宏观缺陷问题[1,2], 目前对准晶材料中的裂纹和位错等问题已有较系统的研究[3,4]. 双周期裂纹的相关问题在经典弹性力学中的研究比较多[5～10], 而准晶材料的双周期裂纹问题至今还未见相关报道。本研究利用椭圆函数和解析函数理论讨论了一维压电六方准晶材料中一类裂纹中心位于矩形顶点呈双周期排列的反平面问题, 得到问题的封闭解。

1 问题分析

一维六方压电准晶材料, 裂纹中心位于矩形顶点上并呈双周期分布的横截面图如图1所示。

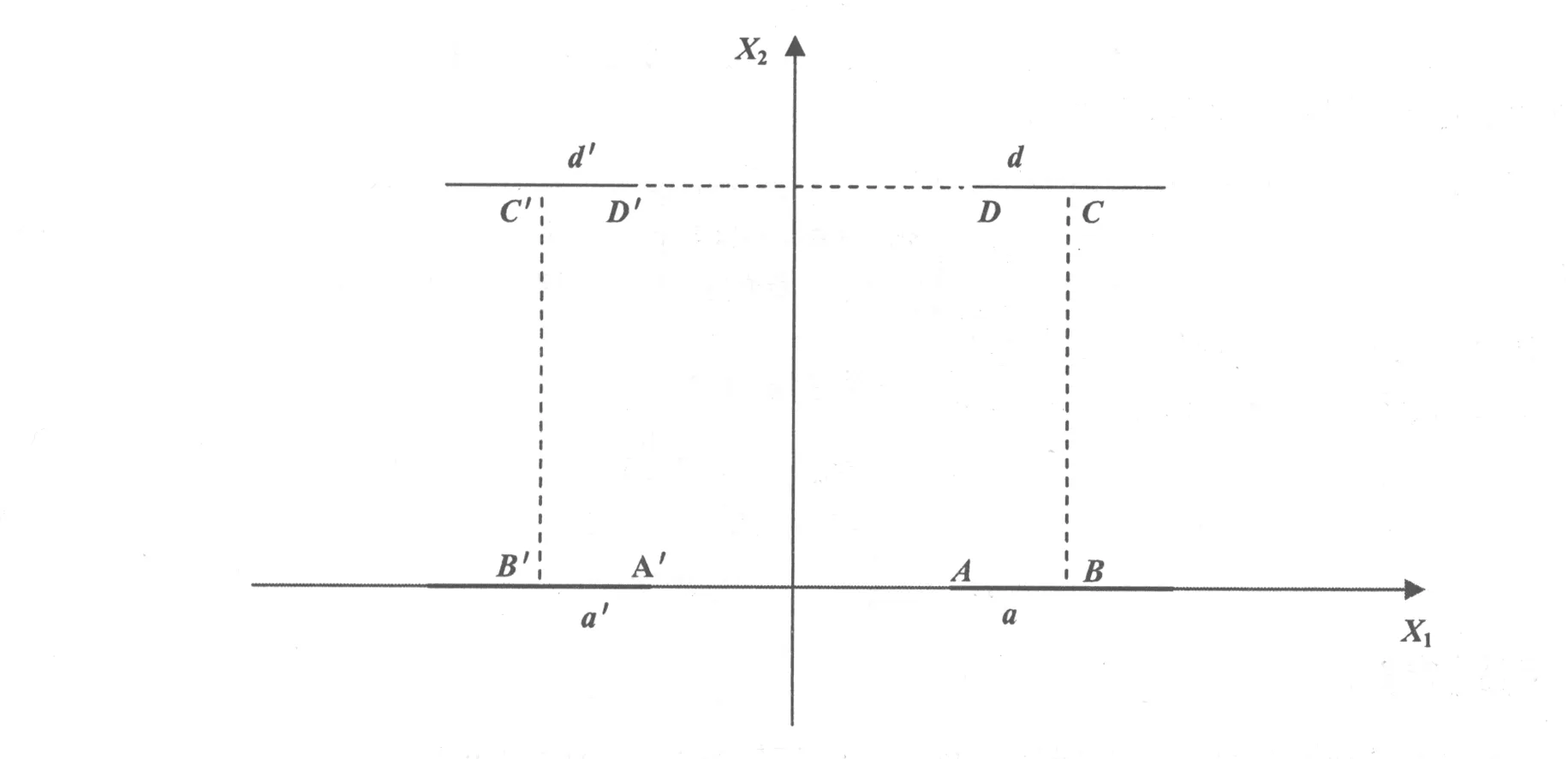
图1 裂纹中心位于矩形顶点

准晶材料的反平面问题, 其反平面应变u3和反平面位移w3以及电势φ可表示为[5]：

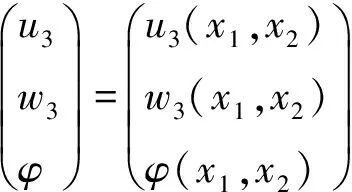
其中，

(1)

本构方程[5]为：

(2)

控制方程为：

(3)

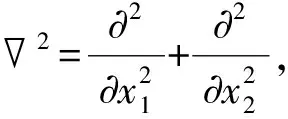
(4)

由于材料参数矩阵行列式L不为零, 有2u3=2w3=2φ=0。这样u3,w3,φ均为调和函数, 可分别用复变量的解析函数的实部表示, 即

(5)

其中z=x+iy为复变量,i为虚数单位。

将(5)式代入(2)式并作复数运算可得，

(6)

2 问题求解

基于对称性和周期性, 可在半胞元ABCDA′B′C′D′(图1)上求解此问题。

对应的边界条件为：

在裂纹AB,CD,A′B′,C′D′上，

σ32=0,H32=0,D2=0

(7)

在AA′,DD′上，

σ31=0,H31=0,D1=0

(8)

在BC,B′C′上

σ31=0,H31=0,D1=0

(9)

利用(6)式, 边界条件(7),(8),(9)转化为

在裂纹AB,CD,A′B′,C′D′上

Im[F′(z)]=0,Im[G′(z)]=0,Im[Φ′(z)]=0,

(10)

在AA′,DD′,BC,B′C′上

Re[F′(z)]=0,Re[G′(z)]=0,Re[Φ′(z)]=0,

(11)

根据裂纹的边界条件知, 在AA′或DD′上的剪应力与远场在周期长度的值一致, 即

(12)

引进保角变换, 将此矩形区域变换到ζ平面的上半平面(图2)。利用施瓦兹克里斯多夫公式有

(13)

式中，A为常数,k为椭圆函数Sn的模数，有关系式

(14)

上述保形映照将物理平面z平面(图1)上的半胞元ABCDA′B′C′D′映成像平面ζ平面的上半平面, 半胞元的边界映射成实轴,映射时特征点的对应关系如图2所示。

图2 保角变化

设BB′=ω1,BC=ω2,则B,C的坐标分别为

则

(15)

(16)

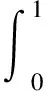
(17)

记

(18)

利用(18)式,(15)与(17)转化为

(19)

从而由(19)式可以确定常数A和模数k。

设AB=a,A′B′=a′,CD=d,C′D′=d′,则

设F1(ξ)=F′(z),G1(ξ)=G′(z),Φ1(ξ)=Φ′(z), 进一步边界条件(10)与(11)转化

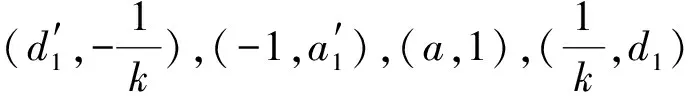
Im[F′(z)]=0,Im[G′(z)]=0,Im[Φ′(z)]=0

(20)

在实轴的其余部分，

Re[F′(z)]=0,Re[G′(z)]=0,Re[Φ′(z)]=0

(21)

利用凯尔狄什-谢多夫公式可得此边值问题的解为

(22)

于是，将(6)式与(22)代入到(12)式得

(23)

这里

(24)

从而

(25)

3 应力强度因子

对压电载荷下含有裂纹的准晶材料, 裂纹尖端的强度因子定义为

(26)

其中

(27)

4 结论与讨论

本次研究给出了压电载荷下无限大一维六方准晶材料中一类裂纹中心位于矩形顶点且呈双周期分布的反平面问题, 并得到了裂纹尖端的应力强度因子。因为几何参数变化的依赖性，需要用数据图表，也就是要做出数值解，但是，对于准晶双周期反平面问题的数值解目前还没有可行的程序，没有相关的文献数据参考，有待于以后进一步研究。

[1] Liu G T, Fan T Y.Governing equations and general solutions of plane elasticity of one-dinensional quasicrystals[J]. International Solids and Structures，2004,41(14): 3 949-3 959.

[2] Fan T Y.A Study on the Specific heat of a one-dinensional quasicrystals[J].Phys Condensed Mater，1991,11(45): 513-517.

[3] Fan T Y.Mathematical theory of elasticity of quasicrystals and its applications[M].Beijing:Science Press,2010.

[4] Fan T Y.Crack and indentation problems for one-dimensional hexagonal quasicrystals[J].The European Physical Journal B,2001,1(1):39-44.

[5] Li X.Application of doubly quasi-periodic boundary value problems in elasticity theory[D].Berlin: Berlin Free Unversity,1999.

[6] 郑可.带裂缝的双周期各向异性平面弹性基本问题[J].应用数学与计算数学学报，1993, 22(1): 16-22.

[7] 郝天护.双周期裂纹反平面问题的一个闭合解[J].清华大学学报，1979,19(3):11-18.

[8] Tong Z H, Jiang C P.A closed form solution to the antiplane problem of doubly periodic cracks of unequal size in piezoelectric materials[J].Mechanics of Materials，2006,38(4):357-360.

[9] Xiao J H,JIANG C P.Exact solution for orthotropic materials weakened by doubly periodic cracks of unequal size under antiplane shear[J].Acta Mechanica Solida Sinica，2009,22(1):53-63.

[10] 常莉红,崔江彦,时朋朋.正交弹性材料中双周期裂纹反平面问题的封闭解[J].应用力学学报，2013, 30(4): 475-479.

[11] 崔江彦. 一维六方准晶的周期问题[D].银川:宁夏大学，2013.