应用Bernstein多项式求解一类分数阶微分方程

李宝凤

（唐山师范学院 数学与信息科学系，河北 唐山 063000）

数学与应用数学研究

应用Bernstein多项式求解一类分数阶微分方程

李宝凤

（唐山师范学院 数学与信息科学系，河北 唐山 063000）

给出了基于Bernstein多项式求解分数阶微分方程的配置方法。首先，在Bernstein级数的截断式中用tα（0＜α＜1）代替t得到分数阶Bernstein级数截断式，采用Caputo分数阶导数构建分数阶Bernstein级数截断式的矩阵形式。其次，把方程中的每一项用分数阶Bernstein级数截断式转换成矩阵形式，选取配置点，得到相应于非线性代数方程的基本矩阵方程。最后得到由条件矩阵形式和基本矩阵方程构成的新方程组，其解给出了截断项为N的近似解，同时给出了基于残余函数的误差分析。举例说明了这种方法的有效性和可行性。

分数阶微分方程；分数阶导数；Caputo分数阶导数；配置方法；Bernstein多项式

1 Introduction

Fractional differential equations are generalized from integer order ones, which are obtained by replacing integer order derivatives with fractional ones. In the last few decades fractional calculus and fractional differential equations have found applications in several differential disciplines. Moreover, a large class of dynamical systems appearing throughout the field of engineering and applied mathematics are described by differential equations of fractional order[1,2]. The fractional differential equations have been solved by means of the numerical and analytical methods such as the Adomian’s decomposition method[3,4], the He’s variational iteration method[5], the Taylor polynomials method[6,7], the Jacobi operational matrix method[8], the homotopyperturbation method[9], the homotopy analysis method[10], the interpolation functions[11], the operational matrix method based on the Legendre polynomials[12], the second kind Chebyshev wavelet method[13], the Bessel collocation method[14]and the Tau method[15].

Recently, the operational matrices of fractional order integration for the SCW[16], Haar wavelet[17], Legendre wavelet[18-19]and Chebyshev wavelet[20]have been developed to solve the fractional differential equations. In this paper, by using good properties of Bernstein polynomials, we shall consider the following initial value problem

WhereLis a linear operator,Nis a nonlinear operator andβDis the Caputo fractional derivative of orderβ.

2 Basic definitions

In this section, we first give some basic definitions and some properties of fractional calculus in[21-26].

Definition 1A real function y(t), t＞0, is said to be in the spaceCu, u∈Rif there exists a real number p＞u, such that y(t )=tpy1(t ), where y1(t )∈C[0,∞). Clearly, Cu⊂Cv, if v＜u.

Definition 2A function y(t), t＞0, is said to be in the spaceif y(n)∈,n∈N.

Definition 3The Riemann-Liouville fractional integral operator of order α≥0 of a functiony,y∈Cu, u≥-1 is defined as

The properties of the operator can be found in [21] and [22]; we mention only the following.

For y∈Cu, u≥-1, α, β≥0, and γ＞-1,

The Riemann–Liouville derivative has certain disadvantages when trying to model real-world phenomena using fractional differential equations. Therefore, we will introduce a modified fractional differential operatorproposed by Caputo on the theory of viscoelasticity[23].

Definition 4The fractional derivative of y(t ) in the Caputo sense is defined as

We note that the approximate solutions will be found by using the Caputo fractional derivative and its properties in this study.

3 Bernstein polynomials and their some properties

The Bernstein basis polynomials of degree n[27,28]are defined by

By using the binomial expansion of (1-t)n-k, it can be written as

Also, the Bernstein basis polynomials of degree n in [0, R] are given by the formula[27]

By using the binomial expansion of (R-t)n-k, we have the formula

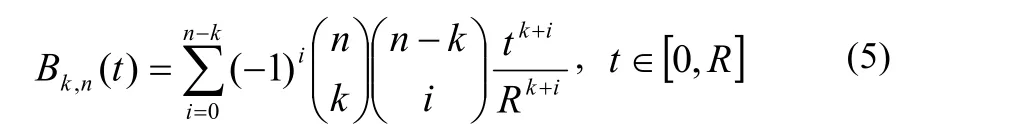
The Bernstein basis polynomials given by Eq. (5) can be written in the matrix form[29-31]

4 Description of the method

By developing the Bernstein polynomial approximation[29-31]with the help of the matrix operations, the collocation method and the Caputo fractional derivative, we obtain an approxi- mate solution of the problem (1)-(2) in the form

Here, 0＜α＜1; ak,k=0,1,2,…,Nare the unknown Bernstein coefficients; Nare any positive integers and

are obtained by putting tαas t in Bernstein polynomials[27]defined by

and clearly, it becomes

We convert the desired solution (6) to the matrix form

By using the matrix form (7), the collocation points and the Caputo fractional derivative (3), we construct the matrix forms for each term of Eq. (1) and the conditions (2). Hence, we transform the problem into a matrix equation which is a system of nonlinear algebraic equations. This system corresponds to a system of the (N+1) nonlinear algebraic equations with unknown coefficients ak,k=0,1,2,…,N. Finally, the approximate solution will be obtained by solving this system.

5 Solution of the problem (1)

To obtain an approximate solution in the form of Eq. (6), we suppose β=kα,0＜α≤1,k∈N+, then Eq. (1) is changed into

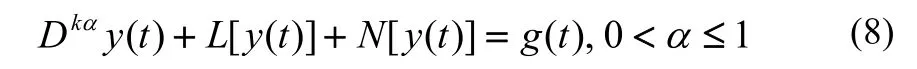
Firstly, let us write the matrix form (7) as

where

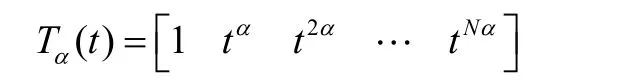
By using the Caputo fractional derivative (3), we write theα-th order fractional derivative of Tα(t) as

where

The kα-th order fractional derivative of Tα( t) is given by the recurrence relation

From (9) and (10), the matrix form of kα-th order fractional derivative of yN,α(t ) is written as

By substituting the collocation points defined by

into Eq. (9), we obtain the system of matrix equations as

In compact form, the above system is written as follows where

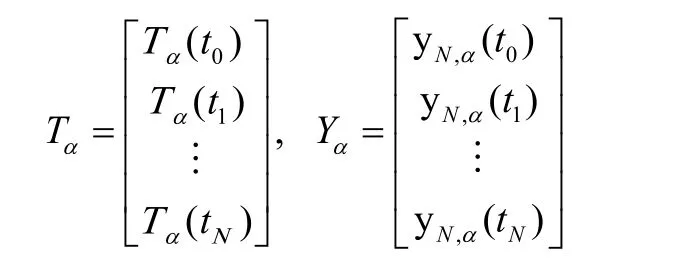
Now, we put the collocation points into Eq. (11) and thus we have the system of matrix equations as below

and the compact form of this system is

Similarly, by substituting the collocation points intoand by using Eq. (13), we obtain

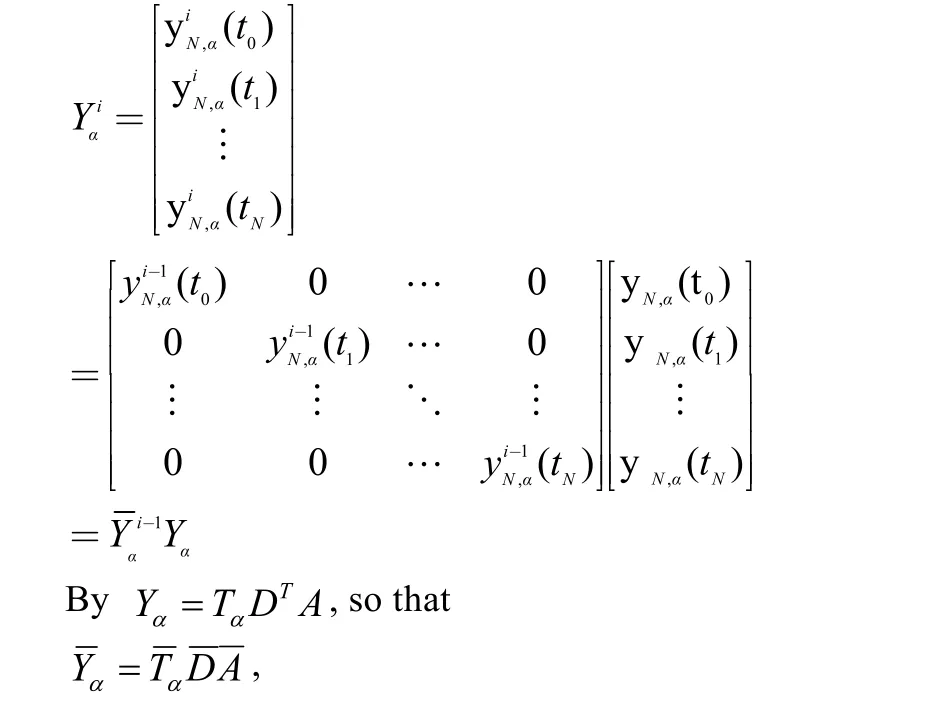
where

We substitute the relation (6) in Eq. (8) and thus we have

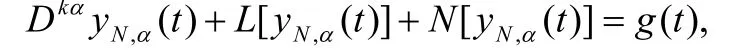
Now, let us put the collocation points into the above equation as below

where

and L is a linear operator matrix of the matrix, N is a nonlinear operator matrix of the matrix.

We place the relations (13)-(14) into Eq. (15) and then we have the fundamental matrix equation

To obtain the matrix form of the mixed conditions (2), let us take t=0 in Eq. (11). Then, the matrix form of the conditions (2) becomes

To obtain the approximate solution of the problem (1) under the conditions (2), we replace the rows of the augmented matrix of Eq. (16) by the row matrices of the augmented matrix of Eq. (17). As a result, the coefficients are determined by solving this system. Hence, by substituting the determined coefficients into Eq. (6), we obtain the Bernstein polynomial solution. Error analysis of the method is established by Theorem 1.

Theorem 1Let yN,α(t ) and y(t) be the Bernstein series solution and the exact solution of the equation (1), respectively. If∈C( a, b], k=0,1,2,…,n +1, then

Proof.Since∈C( a, b], k=0,1,2,…,n +1, By generalized fractional Taylor expansion,

6 Illustrative Example

Here we present an example to illustrative the method, which was performed all numerical computations by a computer program written in Matlab. We consider the following initial value problem in the case of the inhomogeneous Bagley-Torvik equation[32]

where g( t)=1+t subject to the following initial value states y(0)=1,y'(0)=1and β=1.5. The exact solution of this problem is y( t)=1+t. If let β=kα, 0＜α≤1, then k=3,α=0.5.

In this problem, α=0.5. We take N=4 in the form

The collocation point points from (12) are computed as

From Eq. (16), the fundamental matrix equation of the problem is written as

where

From Eq. (17), we compute the augmented matrix form of the initial condition as

New augmented matrix based on the condition is found. Hence, by solving this system, the coefficients matrix are obtained as

The determined coefficients are substituted into Eq. (19) and thus we have

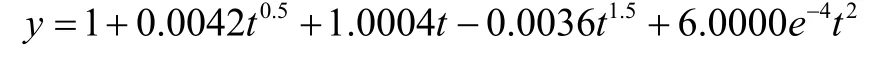
In Tables1, the numerical solutions of our method are compared with the solutions of the exact solution

Table 1 Absolute error of the numerical results with the exact solution forN=4

7 Conclusion

The aim of this paper is to develop an effective and accurate method for solving fractional differential equations, including linear and nonlinear equations. An example is given to demonstrate the powerfulness of the proposed method. Moreover, the method in this paper can also be used for fractional integral- differential equations and other type of equations.

[1] R L Bagley, R A Calico. Fractional order state equations for the control of viscoelastically damped structures[J]. J Guid Control and Dyn, 1991, 14(2): 304-311.

[2] Y A Rossikhin, M V Shitikova. Application of fractional derivatives to the analysis of damped vibrations of viscoelastic single mass systems[J]. Acta Mech, 1997, 120(1-4): 109-125.

[3] V D Gejji, H Jafari. Solving a multi-order fractional differential equation[J]. Appl Math Comput, 2007, 189(1): 541-548.

[4] S S Ray, K S Chaudhuri, R K Bera. Analytical approximate solution of nonlinear dynamic system containing fractional derivative by modified decom- position method[J]. Appl Math Comput, 2006, 182(1): 544-552.

[5] Z Odibat, S Momani. Application of variational iteration method to nonlinear differential equations of fractional order[J]. Int J Nonlinear Sci Numer Simul, 2006, 1(7): 271-279.

[6] Y Keskin, O Karaoğlu, S Servi, G Oturanç. The approximate solution of high-order linear fractionaldifferential equations with variable coefficients in terms of generalized Taylor polynomials[J]. Mathematical and Computational Applications, 2011, 16(3): 617-629.

[7] Y Çenesiz, Y Keskin, A Kurnaz. The solution of the Bagley-Torvik equation with the generalized Taylor collocation method[J] J Frank Inst, 2010, 347(2): 452-466

[8] E H Doha, A H Bhrawy, S S Ezz-Eldien. A new Jacobi operational matrix: An application for solving fractional differential equations[J] Appl Math Model, 2012, 36(10): 4931-4943

[9] N H Sweilam, M M Khader, R F Al-Bar. Numerical studies for a multi-order fractional differential equation [J]. Phys Lett A, 2007, 371(1-2): 26-33.

[10] I Hashim, O Abdulaziz, S Momani. Homotopy analysis method for fractional IVPs[J]. Commun Nonlinear Sci Numer Simul, 2009, 14(3): 674-684.

[11] P Kumar, O P Agrawal. An approximate method for numerical solution of fractional differential equations[J]. Signal Processing, 2006, 86(10): 2602-2610.

[12] A Saadatmandi, M Dehghan. A new operational matrix for solving fractional-order differential equations[J]. Comput Math Appl, 2010, 59(3): 1326-1336.

[13] Y Wang, Q Fan. The second kind Chebyshev wavelet method for solving fractional differentail equations[J]. Appl Math Comput, 2012,218 (17): 8592-8601.

[14] Ş Yüzbaşı. Numerical solution of the Bagley-Torvik equation by the Bessel collocation method[J]. Math Meth Appl Sci, 2012, 36(3):300-312.

[15] S K Vanani, A Aminataei. Tau approximate solution of fractional partial differential equations[J]. Comput Math Appl, 2011, 62(3): 1075-1083.

[16] Y X Wang and Q B Fan. The second kind Chebyshev wavelet method for solving fractional differential equations[J]. Appl Math Comput, 2012, 218(17): 8592-8601.

[17] Y L Li and W W Zhao. Haar wavelet operational matrix of fractional order, integration and its applications in solving the fractional order dierential equations[J]. Appl Math Comput, 2010, 216(8): 2276-2285.

[18] M Rehman, R A Khan. The Legendre wavelet method for solving fractional differential equations[J]. Commun Nonlinear Sci Num Sim, 2011, 16 (11): 4163-4173.

[19] H Jafari, S A Youse, M A Firoozjaee, S Momanic, C M Khalique. Application of Legendre wavelets for solving fractional differential equations[J]. Comp Appl Math 2011, 62(3):1038-1045.

[20] Y L Li. Solving a nonlinear fractional differential equation using Chebyshev wavelets[J]. Commun Nonlinear Sci Num Sim, 2010, 15(9): 2284-2292.

[21] K S Miller, B Ross. An Introduction to the Fractional Calculus and Fractional Differential Equations[M]. New York: Wiley, 1993.

[22] K B Oldham, J Spanier. The Fractional Calculus[M]. Academic Press, New York, 1974.

[23] M Caputo. Linear models of dissipation whose Q is almost frequency independent part II[J]. J Roy Aust Soc, 1967, 13(5): 529-539.

[24] K Diethelm, N J Ford, A D Freed, Yu Luchko. Algorithms for the fractional calculus: A selection of numerical methods[J]. Comput Math Appl Mech Eng, 2005, 194 (6): 743-773.

[25] I Podlubny. Fractional Differential Equations[M]. New York: Academic Press, 1999.

[26] S Momani, Z Odibat. Numerical approach to differential equations of fractional order[J]. J Comput Appl Math, 2007, 207(1): 96-110.

[27] M I Bhatti, P Bracken. Solutions of differential equations in a Bernstein polynomial basis[J]. J Comput Appl Math, 2007, 205(1): 272-280.

[28] E W Cheney. Introduction to Approximation Theory(2nded.)[M]. Providence, RI: Chelsea Publishers, 1982.

[29] O R Işık, Z Güney, M Sezer. Bernstein series solutions of pantograph equations using polynomial interpolation[J]. J Diff Equ Appl, 2012, 18(3): 357-374.

[30] O R Işık, M Sezer, Z Güney. A rational approximation based on Bernstein polynomials for high order initial and boundary values problems[J]. Appl Math Comput, 2011, 217(22): 9438-9450.

[31] O R Işık, M Sezer, Z Güney. Bernstein series solution of a class of linear integro-differential equations with weakly singular kernel[J]. Appl Math Comput, 2011 217(16): 7009-7020.

[32] A Saadatmandi and M Dehghan. A new operational matrix for solving fractional-order differential equations [J]. Comput Math Appl, 2010, 59(3): 1326-1336.

（责任编辑、校对：赵光峰）

The Numerical Solutions of a Class of Fractional Differential Equations by Means of the Bernstein Polynomials

LI Bao-feng
(Department of Mathematics and Information Science, Tangshan Teachers College, Tangshan 063000, China)

A collocation method based on the Bernstein polynomials is presented for a class of fractional differential equations. By replacing t withαt(0＜α＜1) in the truncated Bernstein series, the truncated fractional Bernstein series is obtained and then it is transformed into the matrix form. By using Caputo fractional derivative, the matrix forms of the fractional derivatives are constructed for the truncated fractional Bernstein series. We convert each term of the problem to the matrix form by means of the truncated fractional Bernstein series. By using the collocation points, we have the basic matrix equation which corresponds to a system of nonlinear algebraic equations. Lastly, a new system of nonlinear algebraic equations is obtained by using the matrix forms of the conditions and the basic matrix equation. The solution of this system gives the approximate solution for the truncated limited N. An error analysis technique based on residual function is developed and applied to an example to demonstrate the validity and applicability of the proposed method.

Fractional differential equations; fractional derivative; Caputo fractional derivative; collocation method; Bernstein polynomials

O175.6

A

1009-9115(2014)02-0001-06

10.3969/j.issn.1009-9115.2014.02.001

唐山师范学院团队支撑重点项目（2014D09）

2013-06-03

李宝凤（1971-），女，河北唐山人，硕士，副教授，研究方向为计算数学。