追根究因 方能明理——一道中考选择题的错因分析

☉浙江省宁波市宁波东海实验学校 陈明儒

追根究因 方能明理
——一道中考选择题的错因分析

☉浙江省宁波市宁波东海实验学校 陈明儒

一、缘起

暑假初中数学教师培训会上，其中区内有位Z教师发言，主题是关于2013年宁波市中考数学卷的评价，在讲到第12题（选择题）时，介绍了两种解法，实录如下.

题目：7张如图1所示的长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示，设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a、b满足（ ）.

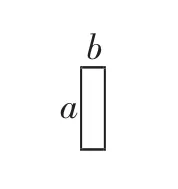
图1

图2

解法1：如图2，记左上角阴影部分的面积与右下角阴影部分的面积分别为S1、S2，AG=x.S=S1-S2，AD=BC=x+a，EC=x+a-4b.S1=3bx，S2=a（x+a-4b）.因此，S=S1-S2=3bx-a（x+a-4b）.由题意知：当BC的长度变化时，x也随之改变，现不妨取x=a，x=2a，因为S始终保持不变，所以，3ab-a（a+a-4b）=6ab-a（2a+a-4b），整理得a2-3ab=0，解得a=0或a=3b.

因为a≠0，则a、b必须满足a=3b.因此，选B.

解法2：前面部分同解法1，不妨取x=a，x=4b，则3ab-a（a+a-4b）=12b2-a（4b+a-4b），整理得a2-7ab+12b2=0，解得a=3b或a=4b.所以，问题的答案是：B或D.而试卷的标准答案是B，Z教师发现解法2有问题，但问题究竟出在哪里呢？他就征询下面听课的老师：“解法2错在哪里？”

二、探究

读者不难发现，解法1与解法2一脉同源，那么问题究竟出在哪里呢？这个问题引起了笔者的思考与探究.首先，想到将两个答案中的等量关系分别代入图2检验.

当a=3b时，将左上角阴影部分平移至右上角（如图3），发现上下两个黑色矩形一边相等且都为3b，另一边长始终相差b，则对应的面积之差为3b2，为定值，符合题意.

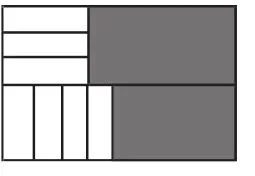
图3

再看，当a=4b时，同样将左上角阴影部分平移至右上角（如图4），上下两个黑色矩形一边相等都为x，另一边长DF与CF相差b，则对应的面积之差为-bx.因此，当BC的长度变化时，x也随之改变，即S=S1-S2=-bx发生改变.所以，a=4b不符合题意.至此可以肯定，解法2是有问题的.

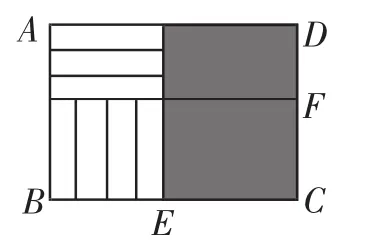
图4

那么，错误究竟在哪里呢？让我们回头看解法1与解法2，发现解题方法一样，但变量x选取的实数值不一样.在解法1中，因为a≠0，所以a≠2a，也就是说，变量x取了两个不同的实数，即在这个过程中线段BC确实发生了变化；在解法2中，a与4b的大小关系不确定，因此，有两种情形，即a=4b与a≠4b.若a=4b，则变量x表面上取了两个实数，实际上只取了一个值，即线段BC的长没变，不合题意.错误的原因找到了，就是解法2犯了一个逻辑错误：把要求证的结论，先进行假设，是一个典型的循环论证.那如何改进、完善解法2呢？其实，只要将假设“不妨取x=a，x=4b”改为“不妨取x=a，x=4b（a≠4b）”即可.

三、再探究

问题找到并解决了，如果作为一个教学的素材，是否本题有更好的解决方案？问题本身还蕴含哪些数学价值？有哪些教学启示？之后笔者对此问题进行了再探究.回顾上述两种方法，本质是变量x取两个不同的正实数，得到一个等量关系，而后化简、整理，导出关于a与b的关系式.那么x取1、2，化简、整理的过程不是更简单吗？

解法3：（前面同解法1）不妨取x=1，x=2，则3b-a（1+a-4b）=6b-a（2+a-4b），整理得a=3b.

解法3中不会出现关于a、b的二次方程，无需因式分解，变形过程简捷，显然，比前面的方案更好.

再回到题目中的题设：“当BC的长度变化时，按照同样的放置方式，S始终保持不变”，因为线段GD为定值，上述题设等价于“当AG的长度变化时，按照同样的放置方式，S始终保持不变”，用函数的视角说明S是关于x的函数.由解法1，可以整理得：

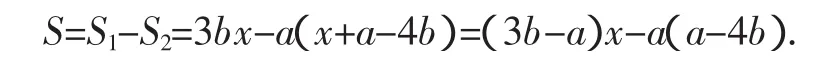
初看，发现S是关于x的一次函数，依据一次函数的性质，S随着x的增大而增大（或增大而减小）.而实际问题是：“当x的长度变化时，S始终保持不变”，因此，一次函数y=kx+b中的k=0，所以，3b-a=0，即S是一个常量函数.至此，就找到了解决本题的一般的代数方案.

解法4：记左上角阴影部分的面积与右下角阴影部分的面积分别为S1、S2.设AG=x.AD=BC=x+a，EC=x+a-4b.S1=3bx，S2=a（x+a-4b）.因此，S=S1-S2=3bx-a（x+a-4b）=（3b-a）x-a（a-4b）.由题意知：当BC的长度变化时，按照同样的放置方式，S始终保持不变.即当x取任意正实数时，S=（3b-a）x-a（a-4b）为定值.因为-a（a-4b）为定值，所以3b-a=0，即a、b必须满足a=3b.

到目前为止，上述想法都纠结在代数领域，所涉及知识不外乎整式、方程及函数，即数与代数的范畴.再看原题目的背景，是个几何图形，提醒笔者从形的角度思考问题的解决方案，经过探究，就有了解法5.

解法5：因为矩形HBEM、矩形FDGN的面积均为定值，当S为定值时，矩形AHFD与矩形HBCF的面积之差也为定值，而公共边HF是变化的，所以，边AH=BH，即a、b必须满足a=3b.

这就是整体的解决方案（即数学中的整体思想）.具体的解题过程如下.

因为矩形HBEM和矩形FDGN的面积分别是4ab、3ab，为定值，所以它们的面积差ab也为定值.因此，当S为定值时，矩形AHFD与矩形HBCF的面积之差也为定值，而实际上矩形AHFD与矩形HBCF的面积之差为AD×AH-BC×BH=3b（x+a）-a（x+a）=（x+a）（3b-a）.当x取任意正实数时，要使代数式（x+a）（3b-a）为定值，3b-a=0，即a、b必须满足a=3b.

考试时学生估计不会想那么多、那么深刻，因为本题是个选择题，那就用解选择题的常用方法：排除法.

当a=3b时，S=S1-S2=3bx-3b（x-b）=3b2，为定值，故选B.

四、几点启示

1.小题目，大价值

2011年版的义务教育数学课程标准新定义“数学是研究数量关系和空间形式的科学”，“整个数学始终围绕‘数’与‘形’这两个概念的抽象、提炼而发展”，这两句话很好地阐释了数学的本质.因此，我们的数学教学、解题研究及命题备考要始终抓住这条主线.本题虽小，是道选择题，但解题过程中时时都需要进行数和形的思维转化.本题的命题意图非常明显：体现数学的本质，体现数学教学的教育价值，考查学生的数学素养，是道难得的好题，再一次让我们体验了“数借形直观，形借数入微”的真谛.

2.小题目，好素材

现在普遍的教师教学生态：忙于备课、上课、批改作业、订正作业（或个体辅导）；教研活动是应付参加的多，有时参加学校的教研活动时还带着作业；教研文章五年内没发表一篇的教师占绝大多数.另一方面，学校及上级主管部门对教师的专业发展都非常重视，其中把教科研的能力作为重要的考核指标.这些教师都说没时间写，最主要的还是说没写作素材.正如裴光亚老师说的：“素材从教学活动中来，这些包括解题、备课、上课、批改作业、教研活动及读书”.笔者的亲身感受是从这些活动中去留意，勤积累，利用休息时间整理，就可以写出包含真情实感的好文章，本文就是一个好的范例.因此，没有理念，无以致远.

3.小题目，大考验

本文中的考题，虽说是道选择题，有些试卷的分类解析把它归结为整式运算，其实从代数知识去深入分析，发现实质上是有关函数的问题；若从形的角度去审视，借助研究几何的重要方法：图形平移，实质上是图形中的整体与部分的关系.这样理解，有助于培养学生的数学素养，提升教师的专业水准.作为一名数学教师，在解题时要站在数学的高度去俯视那些简单问题，做到浅入深出，在教学时又要做到深入浅出，只有这样，才能引领学生进行更高水平的探究.没有知识的高度和厚度，更是无法前行的.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.裴光亚.数学教师的专业发展：在书房与教室间穿行的教研人生［M］.西安：陕西师范大学出版总社有限公司，2013.

3.陈明儒.突出过程孕育 借助推理催化——《锐角三角函数》教学实录与思考［J］.中学数学（下），2013（7）.

4.陈明儒.揆情度理 拒绝平庸——以一道填空题的解题分析为例［J］.中学数学（下），2013（12）.