台湾、英国初中数学教材比较研究*——以英国AQA数学GCSE课本和台湾“部编”初中数学课本为例

☉海南省琼州学院理工学院 王奋平

☉海南省琼州学院理工学院 王冰玉

☉海南省海南中学 王湛卓

台湾、英国初中数学教材比较研究*
——以英国AQA数学GCSE课本和台湾“部编”初中数学课本为例

☉海南省琼州学院理工学院 王奋平

☉海南省琼州学院理工学院 王冰玉

☉海南省海南中学 王湛卓

前言

我国台湾地区自上世纪末开始的基础教育阶段课程改革为岛内数学教育带来了很大变化，九年一贯制数学教材是台湾教育主管部门组织专家统一编写的建议全岛统一使用的教材，吸收了基础与课程改革新课程标准的基本理念和内容要求，很有特色；英国第四学段后的GCSE考试相当于中国的“中考”，所以第四学段和台湾地区国中相当.台湾地区国中每个年级数学教材分为学生用教科书和学生用练习书两本；英国第四学段数学教材一般根据不同学生的数学基础分为基础水平数学教材、中等水平数学教材、高级水平数学教材三类，供不同数学基础的学生选择使用.英国中小学教材编写出版来源很多，教材五花八门，即使是AQA考试委员会也有很多版本的GCSE教材，本文就英国AQA考试委员会使用的由Harper Collns Publisher Limited2007年出版的高级水平数学教材和我国台湾地区九年制义务教育国中阶段数学教材，从内容、知识编排顺序和知识呈现方式几个方面加以比较.

一、台湾、英国初中数学教材内容比较

台湾国中阶段数学教材学生用教科书按照不同年级分为六本，每个年级两本，六本书共20章1084页；英国初中数学教材就用一本书，共27章641页.表1就两地初中数学内容加以列举比较.

表1：台湾和英国初中数学内容

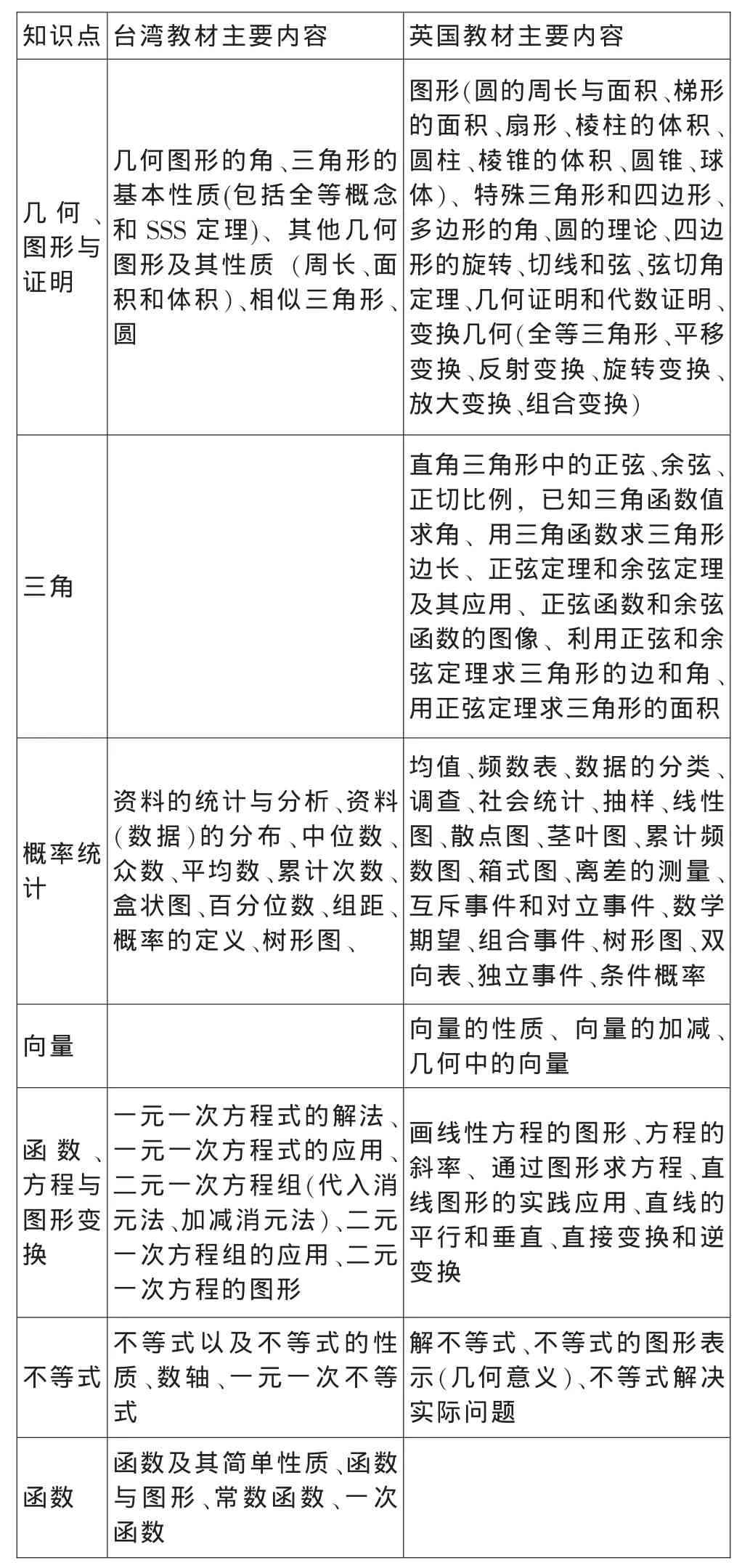
知识点台湾教材主要内容 英国教材主要内容几何、图形与证明几何图形的角、三角形的基本性质(包括全等概念和SSS定理)、其他几何图形及其性质 （周长、面积和体积）、相似三角形、圆三角图形（圆的周长与面积、梯形的面积、扇形、棱柱的体积、圆柱、棱锥的体积、圆锥、球体）、特殊三角形和四边形、多边形的角、圆的理论、四边形的旋转、切线和弦、弦切角定理、几何证明和代数证明、变换几何（全等三角形、平移变换、反射变换、旋转变换、放大变换、组合变换）概率统计直角三角形中的正弦、余弦、正切比例，已知三角函数值求角、用三角函数求三角形边长、正弦定理和余弦定理及其应用、正弦函数和余弦函数的图像、利用正弦和余弦定理求三角形的边和角、用正弦定理求三角形的面积均值、频数表、数据的分类、调查、社会统计、抽样、线性图、散点图、茎叶图、累计频数图、箱式图、离差的测量、互斥事件和对立事件、数学期望、组合事件、树形图、双向表、独立事件、条件概率向量 向量的性质、向量的加减、几何中的向量函数、方程与图形变换资料的统计与分析、资料（数据）的分布、中位数、众数、平均数、累计次数、盒状图、百分位数、组距、概率的定义、树形图、不等式一元一次方程式的解法、一元一次方程式的应用、二元一次方程组（代入消元法、加减消元法）、二元一次方程组的应用、二元一次方程的图形函数画线性方程的图形、方程的斜率、通过图形求方程、直线图形的实践应用、直线的平行和垂直、直接变换和逆变换不等式以及不等式的性质、数轴、一元一次不等式解不等式、不等式的图形表示（几何意义）、不等式解决实际问题函数及其简单性质、函数与图形、常数函数、一次函数

从表1内容可以看到，不管是台湾教材还是英国教材，上述内容基本可以分为四个模块内容：数与量、代数、几何、概率统计.英国教材中“数”的学习比较细致，内容较多，前面三章的内容分别是：数、分数与百分数、比率与比例，第一章主要内容又分为解决实际问题、小数的除法、估算、倍数和因数以及质数、质因数、负数等.英国教材没有专门针对代数式的学习，台湾教材中，代数式的学习却是一个重点.台湾和英国教材中“数”的内容基本相似.台湾教材中没有向量、数列和三角函数，这三项内容在中国大陆数学教材中也在高中才学习，英国教材中却已经开始学习其基本概念和简单性质，对三角函数的学习范围相对更加宽广，包括正弦定理和余弦定理及其应用，高中再继续深入学习，时间跨度很大.英国教材中没有二元一次方程组，令人诧异的是台湾教材中仍然保留了繁分数的概念和运算，繁分数在大陆地区已经作为“繁难偏旧”内容而不再学习.英国教材中没有函数概念和性质，留在高中（第五学段）来学习，而台湾教材中很明确地学习函数，且有常数函数的定义，通过二元一次式和一次函数之间的关系给出线性函数与图形之间的对应关系、二元一次方程组与图形之间的对应关系等.英国教材中没有不等式及其性质，而在台湾教材中，不等式及其性质是重点.几何内容中，英国教材主要学习立体几何和圆的知识，而台湾教材中不学习三角形及其性质、向量及其性质，台湾教材的内容和我国大陆地区各个版本新教材内容比较接近，台湾教材中的证明只针对几何证明，证明方法的学习融合在几何概念和性质的学习中，而英国教材中的证明却有代数和几何证明两种，而且专门有一章内容来学习证明，代数证明在台湾教材中没有专门学习.

英国和台湾教材对欧式几何内容的学习各有侧重，台湾教材继承了中国的传统特点，以学习平面几何中包括三角形全等、圆的性质等中国初中数学传统几何内容为主，而英国教材中平面几何内容很少，除了圆、梯形、扇形的面积外，基本上都是立体几何内容再加上现代几何中的几何变换内容，能明显感受到几何发展的现代步伐.

数列和级数在台湾和英国初中教材中均出现，台湾教材中还专门学习等差数列，英国教材中学习通项公式，这些内容在中国大陆属于高中数学学习的范畴.

二、台湾、英国初中数学知识点编排顺序比较

英国初中数学教材内容基本顺序：数与代数1（多项式、解方程、用解方程的方法转换代数式）→简单三角1→几何与图形→统计1（平均数、频数表、频数图、条形图表示频数、社会调查、抽样）→代数2（展开括号、二次多项式、利用求根公式解二次方程、用完全平方法解二次方程）→三角2（平面和立体图形中的三角、解三角形、特殊角三角函数、求三角形面积）→统计2（折线图、茎叶图、散点图、累计频数图、箱式图、离差测量）→概率→代数3（代数分数、线性和非线性方程组、二次数列）→变量→向量→图形变化→证明，由此可见，英国数学教材各个知识点的安排顺序是按照难度螺旋式上升的，同一个知识点不断地出现，难度逐步增加，这种按照知识难度螺旋式上升安排的模式在全世界各个国家的教材编写方式中比较常见.还有一种叫“块状式”（台湾称为“直线式”）教材，就是一本书中集中一章或几章一次性学完一个知识点所有内容.英国也有很多这样的“直线式”教材，比如，很多出版社出版的高中用微积分教材、三角教材、概率统计教材等，都是本模块内容独立编写成一本书，一次性学习完该模块所有内容.

台湾教材中各个知识点编排顺序：数（倍数、因数）→一元一次方程→二元一次方程组→函数与坐标系→一元一次不等式→多项式及其运算→勾股定理→数列与级数→几何图形及其性质→二次函数→概率统计.

台湾教材中简单的代数知识在倍数、因数、质数、负数等概念之前出现，而英国教材中代数内容均在数的各种概念之后，台湾教材把代数式和方程安排在一起学习，和中国大陆数学教材的安排模式相似，而英国直接学习方程，几乎没有代数式内容作为前奏和铺垫.

对于概率统计内容的学习，英国教材和台湾教材一样，统计学在前，概率在后，第十一章和第十八章分别学习统计学1和统计学2，到第十九章才开始学习概率，台湾教材中虽然概率和统计内容在同一章学习，但是安排顺序仍然是统计内容在前，概率内容在后，这样的安排顺序和中国大陆大学阶段各个版本概率统计教材的知识点安排方式相反.

三角函数的学习顺序：先通过勾股定理学习直角三角形的性质，再通过直角三角形中三边的不同比例来定义正弦、余弦、正切，接着学习用三角函数求三角形的边长，再到平面图形中的三角函数、立体几何图形中的三角函数、求任意角大小、特殊角的三角函数、利用正弦函数求三角形的面积，用两章的容量学习三角函数，难度螺旋式上升.

三、台湾、英国初中数学教材知识呈现方式比较

1.英国教材引导—总结型知识呈现结构有利于提高学习效率

英国教材每章知识内容呈现模式基本相同，章首知识导入：列出本章主要内容概要（overview）→列出本章知识点结构图→列出与本章内容相关的已学知识→通过一个或几个简单的问题帮助学生回忆已学相关知识→进入新知识学习.每节新知识呈现方式也基本相同：本节主要内容和学习目标列举→基本概念或基本定理陈述→相应的例题→相应的练习题→下一个基本概念或定理陈述→相应的例题→相应的练习题，如此反复，最多一节一般不会超过三个基本概念或性质、定理的学习.

台湾初中数学教材数学知识呈现方式和大陆北师大版新数学教材相似，章首没有提前为学生展示本章知识引导或学习目标，直接开门见山进入新知识学习，基本结构如下：以一两个与本节新知识有关的设问引导学生进入新概念、新定理、新性质的思考→新概念呈现→相应的例题→相应的随堂练习→下一个新概念或新定理呈现→相应的例题→相应的随堂练习，如此反复，每节学习的新概念、新定理或性质相对英国教材而言较多，有时候达到五六个概念、性质或定理，有些相对简单的概念，不需要经过例题的学习理解，只需要用一道“动脑筋”的简单思考题来引导学生探究思考后就开始练习；每一节结束后都有一份测试题，题型一般有选择题、填空题、计算题、应用题等四种类型，题量在6～8个左右不等.

由此可见，英国数学教材更加重视学生学习前期的引导，台湾数学教材更加重视后期的检测.相对而言，笔者认为，英国教材更加有利于学生较高效率的学习，尤其是本章知识结构图和每节学习目标的展示，有利于学生一开始就一目了然把握本章的知识脉络和各个知识点之间的逻辑关系.

英国教材代数1中章首就有这样的知识结构图：

同时在第三节“解线性方程”列出学习目标：

在这一节你将会学到：

●解未知数作为分数分子的方程；

●解带有括号的方程；

●解等式两边都带未知数的方程；

●根据已知信息建立方程并解方程.

同时列出与该章内容相关的已学知识内容：

●基本的代数语言；

●合并同类项的方法；

●两项代数式的乘积2m×3n.

每节节首也都列出本节的学习目标，同时学习目标旁边也列出本章学习内容的关键词（Key words），例如在代数1第五章第三节解线性方程中就列举出其学习目标和关键词.

学习目标：

●解分数的分子中含有变量的方程；

●解含有括号需要展开的方程；

●解等式两边均含有指数的方程；

●根据已知条件建立方程并解这个方程.

同时在学习目标右侧列出关键词：括号、两边同时进行相同的运算、方程、方程的解、解决问题.

英国教材每章章末还有一个总结或概括（Summary），概括分为两部分，其一是学习效果分级，其二是应该掌握的知识，例如在线性图像和方程一章就有这样的两部分内容.

对你评级（Grade yourself）：

D.能够通过描点绘制直线图像；

C.能够用点斜式的方法绘制直线；

B.能够绘制一个方程组两个方程对应的图像；

A.能够根据通过一些特殊点的相互平行或相互垂直的两直线确定对应的图像的方程.

你应该知道的知识（What you should know now）：

●如何绘制直线图形；

●通过应用方程组两个方程对应的两条直线的交点求方程组的解；

●如何利用斜率来求出相互平行和相互垂直的直线的方程.

学生根据章首的知识结构图和学习目标，结合每节的学习目标、关键词，能够层层有脉络、步步有指引，有的放矢地学习，按图索骥，根据已经给出的知识脉络学习，同时学生在学习过程中也可以不断地按照知识结构图领会本章数学知识点之间的逻辑关系，复习过程中也能够按照知识结构图来组织各个知识点，有利于加深对整体知识内容的理解，能提高学习效率.因此英国教材的知识呈现方式应该比台湾教材更加有利于学生学习数学，值得借鉴.

2.英国教材中数形结合思想贯穿各个知识点

数形结合思想的合理应用有利于小学和初中等年龄较小、抽象思维能力尚未成熟的学生学习数学，英国教材中有大量数形结合思想渗透在数学知识的学习过程中，例如，在学习一元一次方程时，一开始就学习绘制直线在坐标系内的图形，让学生了解直线和一元一次方程之间的对应关系，再学习根据直线图形来确定方程，接着学习应用数形结合方法解二元一次方程组的方法，最后学习平行直线和垂直直线对应的方程的斜率之间的关系并会求这两种特殊关系的直线对应的直线方程，紧接着继续学习二次函数对应的图像以及其他函数的图像.在学习解不等式时也用数形结合的方法，一元不等式用数轴上有方向的箭头图形表示不等式范围，二元不等式采用直角坐标系内的直线上、下方彩色区域来表示不等式表示的范围，一方面形象而生动，有利于学生正确理解不等式的实质，另一方面也为今后学习线性规划奠定了基础.数形结合思想在英国教材中大量使用，但是在台湾教材中很少看到，解一元一次方程还是用典型的消元法思想，这和我国两岸传统的数学教学思想有关，大陆原来使用的旧大纲教材基本上看不到数形结合解决问题的内容，新课程标准颁布后出版的各版本新教材有所改观，有部分内容用数形结合思想处理，是一个好的开端.

四、例题、习题的结构和配置比较

1.两种教材均根据知识点学习需要随时配置例题和习题

英国和台湾教材例题、习题配置模式基本相同：新概念呈现→相关例题→相关练习题→下一个新概念→相关例题→相关练习题……，如此反复，直到一节所有新概念和新性质、新定理学习结束.英国教材中每个新概念、新性质、新定理配置2个左右的例题，台湾教材中每个新概念、新性质、新定理配置4个左右的例题，但是英国教材例题的解题过程非常详细，同时配以文字解说，有时甚至增加形象的图解说明，而台湾教材中的例题基本上局限于形式化的推理步骤，没有对解题步骤进行过多的文字解释说明，台湾相关练习题称为“随堂练习题”，而英国的新概念相关练习题称为“练习（exercise）”，不同之处是：台湾教材中每节都有一个测试卷，称为“自我评量”，题型有选择题、填空题、计算题、证明题等，而英国教材中只是每章有一个考试卷，称为“考试题（examquestions）”，一般都是计算题和证明题，没有选择题、填空题这样的客观题.

2.两地教材例题、习题数量各有特色

总体上看，台湾教材中每个知识点配置的例题数量比英国教材多，但是英国教材中习题数量远多于台湾教材，台湾每节的“自我评量”，题量在10个以内，英国的“考试题（exam questions）”大题题量一般在10个左右，部分大题包含几个小题，小题题量在20个左右.以两种教材均有的“负数的乘法和除法”一节为例，英国教材中有4个例题，负数乘法和除法各有2个例题，而台湾教材中仅负数乘法就有9个例题，负数除法有6个例题，英国教材中复数乘法和除法的练习题数量为41个，本章最后“考试题（exam questions）”中没有关于负数乘法和除法的习题，而台湾教材中有关负数的乘法和除法的练习题有21个，再加上本节的“自我评量”试卷中包含的5个关于负数乘法和除法考试题，一共26个练习题，远远少于英国教材中相同知识点的练习题.英国教材中习题数量多的特点恰恰体现了中国数学教学中经常提到的“精讲多练”的理念.

五、结论

1.台湾和英国教材都很重视知识点之间的结构和逻辑联系

在台湾教材中，各个知识点的安排顺序非常重视相关知识点之间的逻辑联系.例如，台湾教材中把学习二元一次方程和二元一次方程组的解法放在同一章中来学习，先学习二元一次函数及其图形特征，然后根据二元一次函数的图形特点来学习二元一次方程之间的几何性质，接着再通过两个二元一次函数在坐标系中的图形之间的关系学习二元一次方程组的解法；英国教材中在利用方程对应的线性函数图形交点的方法解二元一次方程组时，也是先学习直线图形与二元一次方程的对应关系，再学习通过图形确定二元一次方程，接着学习利用两个二元一次方程对应的函数图像的交点来求二元一次方程组的解，学完线性函数与它的图像的对应关系后，再学习二次函数、双曲线、三次函数、不规则函数等各类函数的图像及其简单性质，层层推进，难度逐步螺旋上升，前者是后者的基础，后者是前者的延伸和升华，知识面广泛而且符合初中学生的学习心理.

2.英国教材比台湾教材更加“形式化”

从两地教材知识点呈现方式看，台湾教材比英国教材中有更多的现实生活和生产情境例题和背景知识来支持相关知识点的学习，而英国教材中很少见到现实情境的例题.例如，台湾教材中学习坐标系中的点的坐标时，就举了教室里各位同学座位的纵向和横向位置符号数组来说明点的坐标的意义，用投篮时篮球抛出后的轨迹来说明抛物线的几何意义，学习相似形时，是通过讲述古埃及流传的科学家与哲学家泰利斯（Thales）通过测量自己的影子的长度来度量金字塔的高度的故事来学习的.总体上看，不管是台湾教材还是英国教材，都比大陆各个版本的数学新教材更加“形式化”.

3.英国教材比台湾教材更加体现出“精讲多练”的教学思想

从两种教材中配置的例题和习题的数量比较看，英国教材更加注重学生对相关问题的练习，英国教材设计出的练习题不但数量多，而且体现出“变式”训练思想，各种练习题题型多样，通过多次习题的训练不断强化学生对概念的理解.这种模式值得我国教材在完善过程中思考.

六、对我国教材改革的启示

1.英国教材引导和总结结构模式有利于学生自学和提高学习效率

英国教材中每章、每节都有学习目标、关键词等，章末有总结和概括，有利于引导学生自学，同时也有利于学生在学习过程中参照学习目标和概括，掌握各个知识点之间的逻辑关系，加深对各个相关知识点之间基础和递进关系的理解，提高学习效率.我国各个版本数学教材一般均有章末总结和概括，但是缺乏章首、节首学习目标的列举和引导，如果能够学习英国教材模式，增加章首和节首的引导，应该会有更好的学习效果.

2.教材中生活、生产实际情景与数学理论知识结合要恰当和适时

英国教材部分章节结束后有“问题解决（solving problem）”一节，专门培养学生应用数学知识解决实际问题的能力，台湾教材中也有很多数学与实际问题结合的例子.对照我国大陆地区各个版本的数学教材，实际情景与数学理论结合的程度要远高于台湾和英国教材，实际情景的例子也更多，对于初中学生而言，能结合实际问题情境来学习数学有利于学生对数学知识的理解，但是要恰当地选择合适的实际问题，不能牵强附会，也不能数量过多，毕竟，“形式化”是数学的基本特征之一，不能为情景化而情景化，过犹不及.

3.英国教材中的学习内容知识面宽广的特点值得借鉴

从英国教材内容看，英国教材中专门有“证明”一章，而且分为代数证明和几何证明两类，三角函数的学习中，英国教材知识面比较宽泛，不但有平面几何图形中的三角函数，而且也同时学习立体几何图形中的三角函数、正弦函数和余弦函数的图像、正弦定理和余弦定理及其应用等，而且学习数列及其通项公式，英国教材的做法可以让学生开阔视野，了解到三角函数宽广的使用范围，让初中学生从总体上一次性领略三角函数的各种性质，虽然可能容量过大，但是如果学习方法得当，应该会对数学功底较扎实、数学兴趣较高的同学有很大帮助，为他们今后的持续学习奠定宽广的基础.

*该文是全国教育科学 “十二五”规划2012年度单位资助教育部规划课题：“高中数学教科书整体知识结构国际比较研究（FDB20423）”的成果之一.