经验打底画板助力——八年级《13.4 课题学习最短路径问题》教学设计<br/>

经验打底画板助力——八年级《13.4 课题学习最短路径问题》教学设计

2014-02-01山东省滨州市北镇中学初中部邢成云

中学数学杂志 2014年4期

关键词：饮马画板轴对称

☉山东省滨州市北镇中学初中部邢成云

经验打底画板助力
——八年级《13.4 课题学习最短路径问题》教学设计

☉山东省滨州市北镇中学初中部邢成云

一、前提

1.学情分析

（1）认知基础.

在七年级已经研究过“两点之间，线段最短”、“垂线段最短”等最短路径问题以及有关平移的基本知识，在本章的前面学生也初步掌握了作点关于某直线的对称点，所有这些内容构成了本节课的认知基础.

（2）活动经验.

通过初中学段一年多的学习，学生已经有了图形变换以及模型构建的意识，获得了初步的数学化之思维转化这一数学活动的经验，具备了一定的主动参与、合作交流的意识和初步的观察、分析、归纳、猜想和解决问题的能力.

2.教材分析

本节是“课题学习最短路径问题”，是本章的最后一节.教科书在这一节中安排了两个问题，分别是“牧马人饮马问题”和“造桥选址问题”，解决这两个问题的关键是通过轴对称和平移等变化把问题转化为关于“两点之间，线段最短”的问题，在解决这两个问题的过程中渗透了“化归”的思想.

3.教学目标

通过探究1、探究2进一步熟悉轴对称作图以及平移变换作图等基本技能，体会如何以这些素材为载体，利用本章所学的轴对称等知识解决一类实际问题——选择最短路径问题，在观察、操作、想象、论证、交流的过程中，获得解决此类问题的基本套路及经验，发展空间观念，激发内在兴趣.

4.教学重点与难点

重点：探究1的思路获取及问题解决是重点.

难点：探究2的解决是难点.

5.教学方法

问题——探究教学法（几何画板辅助）.

通过史料创设问题情景，给学生提供了广阔的思考空间.引导学生在动手（作图）操作中调整自己的思路、想法，探寻出解决问题的思维路径，在几何画板的支持下，增进体验，帮助学生探索、发现、验证等，然后在拓展活动中迁移使用所获得的基本经验，力求达到深入领会其应用价值的目的.

二、教学过程设计

1.以史创境，引趣入题

设计意图：通过“将军饮马”问题，烘托问题情境，在历史经典中唤起学生的兴趣，激发学生探寻的欲望.不求学生能立即获得答案，主要定位于鼓舞斗志及问题的取向，把学生引领到研究的航道上来.

传说在古罗马时代的亚历山大城有一位精通数学和物理的学者，名叫海伦.一天，一位将军专程去拜访他，向他请教一个百思不得其解的问题.将军每天都从军营A出发（如图1），先到河边l饮马，然后再去河岸的同侧B开会，他应该怎样走才能使路程最短？据说当时海伦略加思索就解决了它.同学们，你知道问题的答案吗？你能想象出海伦当时是怎样解决的吗？

教学说明：一般来说，学生不会张口就能回答，除非已经预习.因此，不论学生怎样回答，我们都要作积极地回应，如适切的评点、激励等，把学生的好奇心给撩拨起来，然后让学生在这种积极心下展开探究，发挥好其助推作用.

2.问题引领，层级递进

设计意图：为了落实好两个核心探究，通过设置基本问题作为先行组织者，在温故中实现引新，为展开探究提供知识、方法及经验的支持.

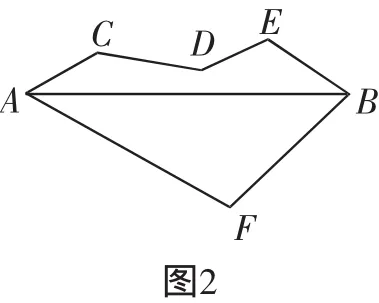
问题1：如图2所示，从A地到B地有三条路可供选择，选择哪条路路程最短？你的理由是什么？

共识：线段AB，因为“两点之间，线段最短”.

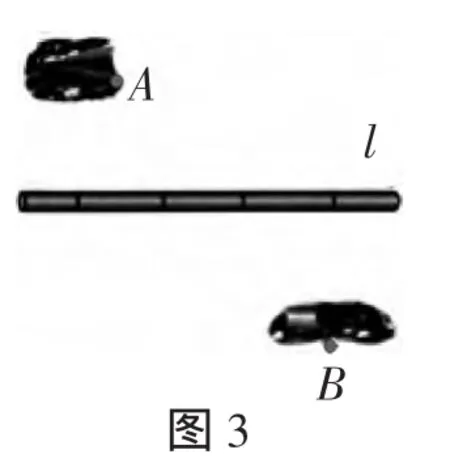
问题2：如图3，要在燃气管道l上修建一个泵站，分别向A、B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？原因是什么？

共识：连接AB，交直线l于点C，点C即为泵站的位置.原因仍然是“两点之间，线段最短”.

教学说明：问题1的回答估计没有问题，但对于问题2可能会出现一类错误：由A向直线l作垂线段，垂足为C，认为C是泵站的位置.此时可通过追问缘由的方式引起学生对最短的探寻，实际上这个状态对应的管线长为AC+CB，而连接AB交直线l于点C时的管线长为线段AB，很显然，根据“两点之间，线段最短”或“三角形中，任意两边之和大于第三边”，可以推翻原有的错误认识.总之，要关注现场的生成资源并有效利用，以保预设与生成的和谐.

三、画板支持，手脑并用

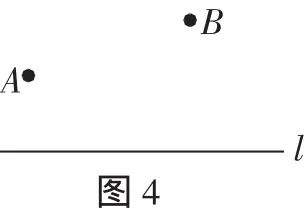
探究1：如图4，牧马人从A地出发，到一条笔直的河边l饮马，然后回到B地.牧马人到河边的什么地方饮马，可使所走的路径最短？

设计意图：设置问题1增进迁移，实现同侧最值问题向异侧最值问题的转化，问题2通过验证与证明实现合情推理向逻辑推理的过渡，期间需要几何画板的功能支持.

问题1：前面我们已经解决了A、B两点在直线两侧的最短问题，下面请同学们思考并尝试，若这两点居于直线的同侧，该怎样找到那样的点P，使得AP与BP的和最小？

分析：在河边饮马的地点有无穷多处，把这些地点与A、B连接起来的两条线段的长度之和，就是从A地到饮马地点，再回到B地的路程之和.现在的问题是怎样找出使两条线段长度之和为最短的那个点来.

预设思路：（化异侧为同侧）先作点A关于直线l的对称点A′，连接BA′，交l于P，则P点即为所求.

问题2：若找到了那样的点，请证明结论的正确性.

教师用几何画板验证后再展开证明的探索.

证明如下.

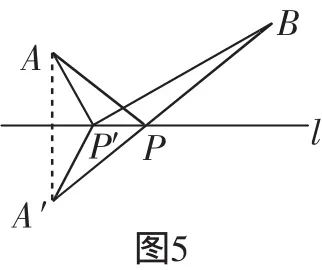
证明：如图5，在直线l上取一点P′（异于点P）.

根据轴对称的性质，可知AP′= P′A′，AP=PA′.

则AP′+P′B=A′P′+P′B＞A′P+ PB=AP+PB.

由此可知：A到B经P点距离最短.

教学说明：通过学生的尝试，提出大胆的猜想，而后利用几何画板的测量功能，度量出AP+BP，然后拉动点P，记作点P′，度量出AP′+P′B ，呈现它们的大小，印证AP+BP最短.最后通过师生交流，形成两条基本经验：（1）此类问题的解答，实际上就是通过轴对称变换，把A、B在直线同侧的问题转化为在直线的两侧，从而可利用“两点之间线段最短”加以解决；（2）在证明最大或最小问题时，往往需要另找一个量与要求证的最大或最小量进行比较来证明.

同步练习：

（1）对课始的问题来说，你知道海伦是怎样解决的吗？

（2）八年级某班同学做游戏，在活动区域边放了一些球，如图6，则小明按怎样的路线跑，去捡哪个位置的球，才能最快拿到球跑到目的地A处？

答案：（1）如图7所示的方案.

（2）如图8所示：路线为小明—P—A.

教学说明：有了探究1的引路，要求学生独立完成两个练习，然后交流结果，以印证解题的基本套路，巩固刚刚获得的基本经验.

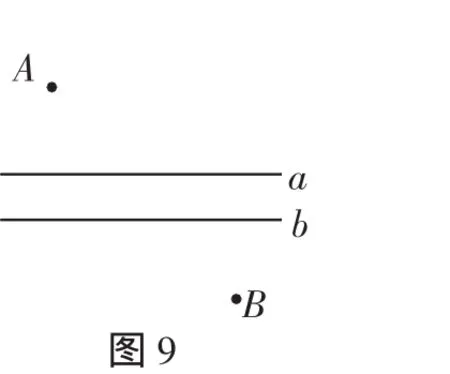
探究2：（造桥选址问题）如图9，A和B两地在一条河的两岸，现要在河上造一座桥MN，桥应造在何处，才能使从A到B的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直）

设计意图：通过设置问题3、4，在探究1获得的经验基础上，把问题引向深入，使得平移变换自然呈现，进一步体现图形变换在最短路径问题中的价值.

问题3：本问题又变成了点在直线两侧的问题，但一条直线拓宽成了一条河，请同学们思考，要在河上造一座桥MN，桥应造在何处，才能使从A到B的路径AMNB最短？

分析：由于河岸宽度是固定的，造的桥要与河垂直，因此路径AMNB中的MN的长度是固定的.可用几何画板探测这样的最小值是否存在.若存在，探测在哪里取得.现场具体操作如下.

（1）画直线a，过a外一点画直线b∥a，用a、b表示河两岸，在河岸的两侧各取一点A、B ，在a上任取一点M，作MN⊥直线b，垂足为N，MN即可表示桥的位置，连接AM、NB，则AMNB可表示A到B的路径，如图10；

（2）度量线段AM、MN、NB的长度，并计算它们的和；

（3）拖动点M，可以发现AM+MN+NB的值会发生变化，且有一个最小值.

获得结论：确实存在一个位置，使得AM+MN+NB的值最小，此时对应着路径AMNB最短.

方案探索：从几何画板呈现的数据以及刚才的分析可知，无论桥建在何处，其长度是固定的，因此要使AM+ MN+NB的值最小，只需AM+NB的值最小即可，关键是这一段如何体现.实际上可把这段宽度看作是一条直线变宽形成的，如此一来就和平移挂起钩来，这样方案就有了.

既成画法：（1）将点A沿与河垂直的方向平移MN的距离到A1；

4.反观课堂，提炼小结

问题清单如下所示.

（1）将军饮马类问题解决的基本套路？

达成共识：就是通过轴对称变换，把两点在直线同侧的问题转化为在直线两侧的问题，从而可利用“两点之间，线段最短”加以解决.

（2）通过探究2和拓展练习，我们在造桥选址问题上已经获得了哪些经验？

达成共识：对于造桥选址问题，要使所得到的路径最短，就是要通过平移变换，使除桥长不变外所得到的其他路径经平移后在一条直线上.

（3）解决路径最短问题时，我们常用的图形变换是什么？目的何在？

达成共识：通常借助轴对称变换、平移变换等，把问题转化为“两点之间，线段最短”的模型去解决.

5.布置作业

略.

6.拓展练习

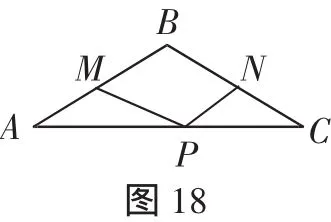
（1）如图18，在等腰三角形ABC中，∠ABC=120°，点P是底边AC上一个动点，M、N分别是AB、BC的中点，若PM+PN的最小值为2，则△ABC的周长是（）.

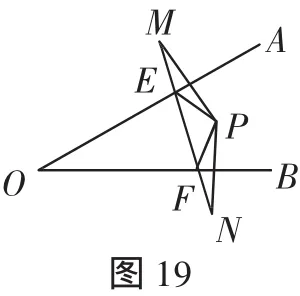
（2）如图19，点P在∠AOB的内部，点M、N分别是点P关于直线OA、OB的对称点，线段MN交OA、OB于点E、F，若△PEF的周长是20cm，则线段MN的长是________.

三、评价与反思

本节课通过经典史料设问，创设认知冲突，而后利用“线段公理”这一先行组织者，从学生已有的知识出发，通过问题引路，借助几何画板，进行了两个探究活动的教学设计，整节课充满学生的尝试、辩驳，合情与逻辑携手、预设与生成和声，现代技术的支持为课堂增色.整体观之，有三大特色.

1.已有经验的先行组织

数学基本活动经验充实了与时俱进的新“四基”，要展开探索与研究，学生已有的知识经验起着先导的作用，有效利用能发挥它们的引领作用.引桥的搭建、思维缺口的弥合都离不开经验的策动力，大胆的猜想源于借助已有经验的认知分析，数学活动经验涉及数学活动中的体验、理解和感悟等，活动经验的迁移，也是厚积薄发的过程，这种能迁移的活动经验，是凭借已有经验，在解决数学问题的过程中，把经验转化为新情景下的思路，通过往复“留痕”及反复强化、沉淀形成的，这样的数学活动经验，其迁移性能才会好.三个教学环节中的问题解决过程设计，就充分展现了已有经验不断迁移应用的历程，有浓浓的课题学习的味道.