将探究进行到底——由角的分割引发的三角形相似问题的探究

☉江苏省东台市实验中学 邹施凯

将探究进行到底
——由角的分割引发的三角形相似问题的探究

☉江苏省东台市实验中学 邹施凯

一、引言

2013年11月，江苏省教研室网络教研平台——“教学新时空”栏目邀请了几位资深嘉宾，对“数学探究”教学做了一次专题研讨，旨在通过对数学探究的深入研究，进一步促进广大教师对探究教学的思考，增强大家对探究教学的认识，笔者有幸全程参与了这次活动，感触颇深.下面就让我们从本次活动的开场白出发，结合角的分割引发的三角形相似问题，谈谈探究性教学.

主持人：请问邹老师，你选择“数学探究”为今天研讨的主题，原因是什么？

笔者：从事数学教育二十多年，最让我对数学教育充满感情的是“三维数学思想”，它是我通过多年实践所积淀的教学主张，“数学探究”式学习正符合这样的思想理念.在“三维数学思想”的指引下，我和我的同事都尝到了“数学探究”的甜头，它打开了学生的思维空间，提高了学生解决问题的能力.另外，“新课标”将课程目标分为“知识技能”、“数学思考”、“问题解决”和“情感态度”四个方面.目前，虽然大家对以上四个目标都已经有了一定的认识，但并不代表对每一个标准和每一个标准的支撑点的理解都很到位.因此，我想借助今天这个平台，就这个话题与大家进行交流，共同提高对“数学探究”教学的认识.

嘉宾A：从数学探究课的本质研究看，数学探究具有一定的挑战性，往往解决一个探究性问题并不困难，但如何设计探究情境、组织问题串却大有文章可做.

嘉宾B：从数学探究课的实施现状看，在实际教学过程中，由于数学探究式教学所用时间与常规用时的矛盾，使得实际探究课有很大的“机动性”，常常有说起来重要，但忙起来却顾不到的现象发生，所以认真研究“数学探究”教学很有必要.

主持人：下面先让我们一起来观看“由角的分割引发的三角形相似问题的探究”的教学视频.

二、教学片段实录与点评

1.新课的导入

师：同学们，数学是一种冰冷的美丽，今天我将和大家一起通过角的分割来探究这样的美丽，在探究之前我们一起来回忆课前讨论的问题.

花圃问题：如图1，校园内有一块等腰直角三角形和一块正三角形的空地，现打算把它们分别种植成三种不同颜色的花圃，且使得每种颜色的花圃所形成的图形为相似的三角形，你能帮忙设计一下吗？

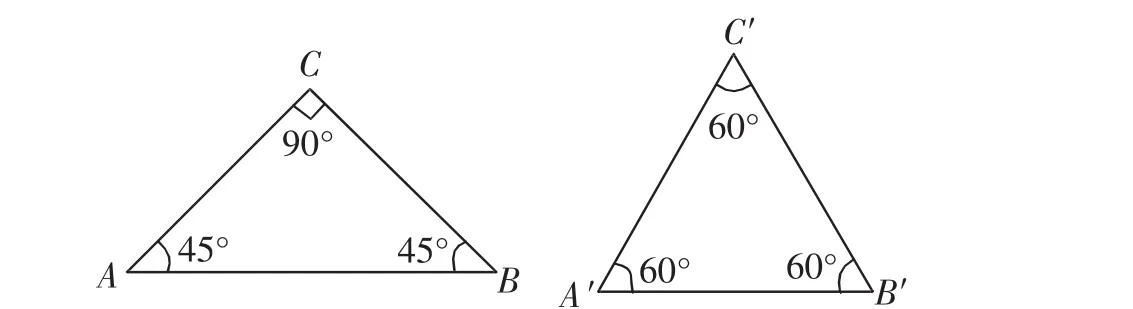
图1

生1（代表）：看起来似乎无从下手，我们小组的同学还没有想到可行的办法.

生2：我们小组也是.

师：通过今天这节课的探究，我们就可以解决此类问题了！

点评：教者在课前先抛出问题，让学生有充分的思考时间，使学生基本处于思考，多数处于迷茫，部分处于“绝望”之中，充分激发学生的求知欲望，使其产生探究问题、解决问题的迫切愿望，为探究做心理上的准备.

师：如图2，（PPT出示）在△ABC中，∠A=50°，∠B=60°，△A′B′C′中，∠B′=60°，∠C′=70°，这两个三角形相似吗？为什么？

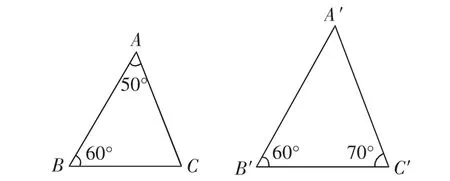
图2

生3：相似，因为在这两个三角形中能找到两对角相等.

师（追问）：能具体一点吗？

生3：在△ABC中，运用三角形内角和定理可求得∠C=70°，结合条件可知∠B=∠B′，∠C=∠C′，所以两三角形相似.

师：回答得很好！

点评：设计如此简单的题目的目的是让所有学生熟悉两个知识点：①三角形内角和定理；②判断两个三角形相似的最常用的方法之一——找两组角对应相等.这两个起点低、发散性强的基础知识，能增强所有同学积极参与问题探究的自信心，为探究问题做知识上的准备.

2.建模的思想

师：下面，让我们一起看看课本上的问题（八年级下册课本P123第15题）：如图3，有两个分别涂有黄色和蓝色的△ABC和△A′B′C′，其中∠C=∠C′=90°，且两个三角形不相似.问：能否分别用一条直线分割这两个三角形，使△ABC所分割成的两个黄色三角形与△A′B′C′所分割成的两个蓝色三角形分别对应相似？如果能，请设计出多种分割方案；如果不能，请说明理由.

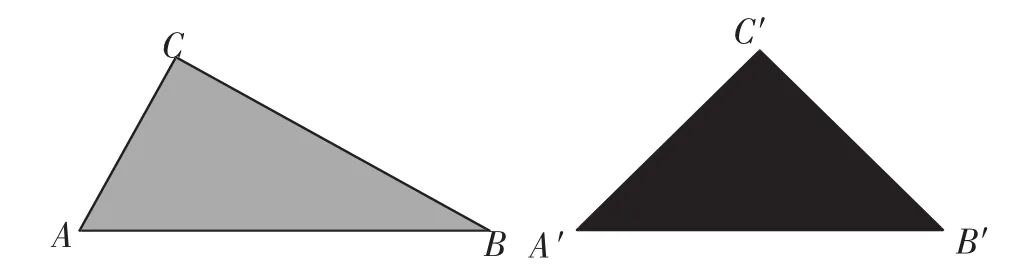
图3

师：假设∠A=60°、∠B=30°，∠A′=∠B′=45°，现在就请大家分组合作，用不同的方法对图形进行分割，并完成在导学案中.

小组1分割图形展示（如图4）.

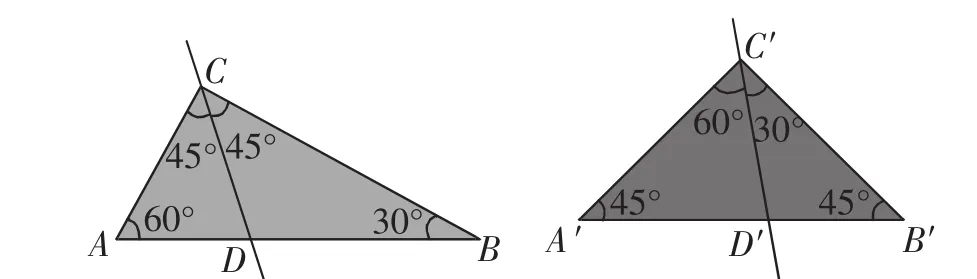
图4

小组2分割图形展示（如图5）.

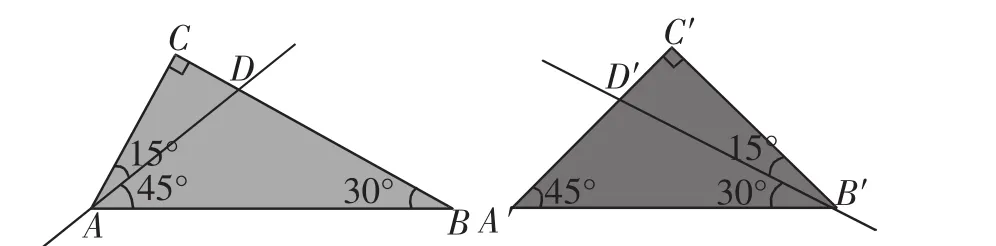
图5

师：请这两个小组的同学对各自的分割方法作适当的说明.

生4：我们在一个三角形最大的角中割出另一个三角形的最小角.具体思路为：如图4，在∠ACB中割出一个45°角，在∠A′C′B′中割出一个30°角，“生产”出的都含有45°和30°的两个三角形必然相似，剩下的两个三角形经验证也相似.

生5：我们先分别找出两个三角形中的最小角30°和45°，然后在两个三角形的次小角中分别割出45°角和30°角，形成如图5所示的△ABD与△A′B′D′，这两个三角形相似，△ACD与△B′C′D′也相似.

师：说得都很好！你们的分割有一个共同的特点：（稍停顿）“割大出小”.请大家继续思考：如果我们抓住△ABC和△A′B′C′中的∠A+∠B=∠A′+∠B′（板书），即60°+30°=45°+45°，移项后就得到60°-45°=45°-30°=15°，你能结合图形解释分割的依据吗？

生6：“60°-45°”就是在△ABC的60°角中割出45°角；“45°-30°”就是在△A′B′C′的45°角中割出30°角，从而形成△ABD中有45°角，△A′B′D′中有30°角，并且其差均为15°，再结合∠C=∠C′=90°，可得所分割成的两对三角形分别对应相似.

点评：确定好三角形锐角的度数后，学生的探究容易上手，同学们几乎都能看出“-”的几何意义，在分割的过程中体会数形结合的思想方法.另外，从课本习题出发，让学生分组展开探究，从中发现、归纳分割图形的方法，为后续探究积蓄技能，体会“我中有你、你中有我”的分割思路.

师：归纳得很好！请大家用这样的分割思路来探究下面的问题.

探究1：把课本习题中的条件改为：如图6，在两个锐角三角形中，如果∠C=∠C′=60°，其余条件不变，是否可以分割？

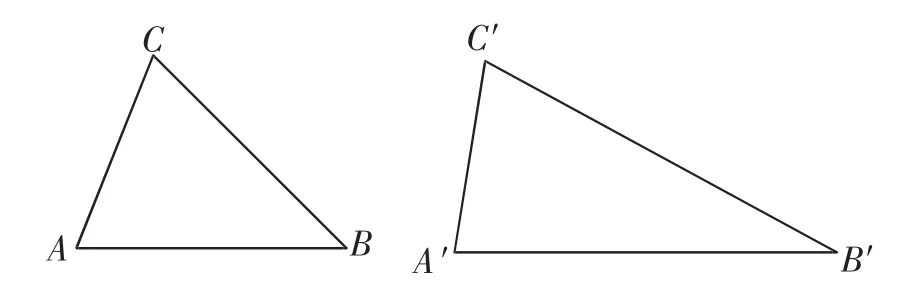
图6

师：同学们，为了便于分割，我们仍然可以假设两个三角形中未知角的度数.

生7：假设∠A=70°、∠A′=85°，则∠B=50°、∠B′=35°.

师：好！请大家在这位同学的假设前提下进行探究.

教学说明：一会儿工夫，各小组纷纷完成自己的作品，其中某小组作品展示如图7所示.

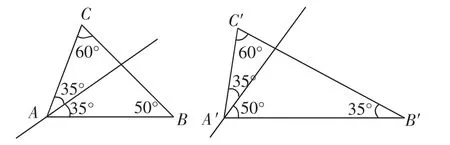
图7

生8：由条件可知：∠A+∠B=∠A′+∠B′=120°，即70°+50°=85°+35°，然后找出较小角度数：35°和50°，移项得：70°-35°=85°-50°.其意义就是在70°角中割出一个35°角，在85°角中割出一个50°角，且使得割出的35°角和50°角在同一个三角形中.

师（追问）：如果不给出两个三角形中另外4个角的度数，你还能分割吗？

生8：能.

师（追问）：为什么？

生8：因为原来的两个三角形不相似，所以不可能出现第二组角对应相等，无论角的大小如何变化，我们都可以在较大角中割出较小角.

生9：老师，我还有一种不同的分割方法，就是把50°角和85°角进行分割.

师：请展示一下你的作品，并作简单的说明.

生9：由70°+50°=85°+35°，可以得到：50°-35°=85°-70°=15°，如图8，就是在50°角中割出一个35°角，在85°角中割出一个70°角，且使得割出的35°角和70°角在同一个三角形中即可.

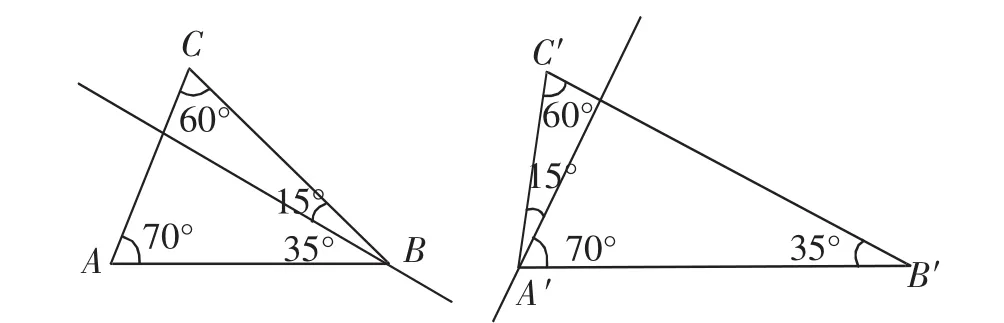
图8

师：太棒了！同学们，这位同学已经完全掌握了分割的方法：“找小割大”，真不简单！有了这次分割的经验，请大家继续探究下面的问题.

探究2：如图9，在两个钝角三角形中，如果∠C=∠C′=120°，其余不变，是否可以分割？

图9

点评：当学生归纳出分割的思路“先找小角，后割大角”后，学生品味到了成功的喜悦，探究的信心更足了！很多同学面露喜色，跃跃欲试！

一会儿工夫，不少小组已经分割成功，现选两小组作品展示如下.

A组：

图10

生10：如图10，我们假设∠A=40°、∠A′=50°，则∠B=20°、∠B′=10°.由∠A+∠B=∠A′+∠B′，即40°+20°=50°+10°，移项得：40°-10°=50°-20°=30°，所以在40°角中分割出10°角，在50°角中分割出20°角，且使得分割出的10°角、20°角在同一个三角形中，分割剩下的30°角和120°角在同一个三角形中，形成两对三角形分别对应相似.

生11：也可以利用三角形的外角分别计算出∠1、∠2均为30°.

B组：

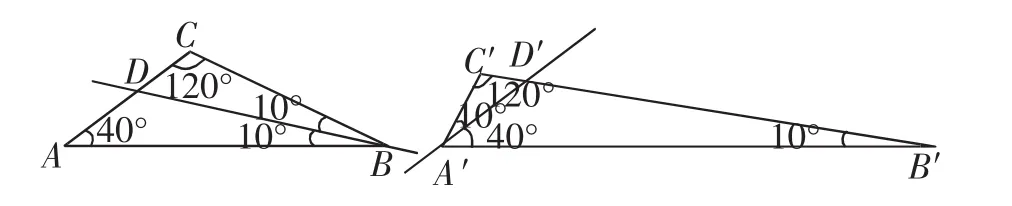
图11

生12：如图11，我们小组也假设∠A=40°、∠A′=50°，则∠B=20°、∠B′=10°.由∠A+∠B=∠A′+∠B′，即40°+20°=50°+10°，移项得：20°-10°=50°-40°=10°，所以在20°角中分割出10°角，在50°角中分割出40°角，且使得分割出的10°角、40°角在同一三角形中，分割剩下的10°角和120°角在同一三角形中，形成的两对三角形分别对应相似.

师：两组同学的分割方法都是正确的，同学们能先抓住小角再移项，用“数”的运算去指挥“形”的分割，太好了！请大家接着思考.

探究3：就以上直角、锐角、钝角三角形，你能否分别总结出一般性结论？

生13：这三种三角形都能分割…….

教学说明：学生叙述的同时，老师边补充边板书，使大家形成共识，归纳出阶段性的结论.

结论1：任意两个三角形不相似，只要有一组角对应相等，都可分别用一条直线分割这两个三角形，使分割得到的两对三角形分别对应相似.

师：同学们，我们正行走在美丽花圃的途中，离解决花圃问题已经不远了，请大家接着探究下面的问题.

点评：在成功分割两个直角三角形后，接着分割两个锐角三角形和两个钝角三角形，学生在已有经验的基础上，运用已有方法，运用类比思想进行探究，为进一步推广分割的方法进行有效的验证，形成技能，也为后续探究再做准备.另外由直角三角形到锐角三角形，再到钝角三角形，体现了由特殊到一般的数学思想方法.

3.辩证的思维

探究4：对探究2中的两个钝角三角形，如果∠C=∠C′=120°，能否分别用两条直线分割这两个三角形，使得被分割成的三对三角形分别对应相似？

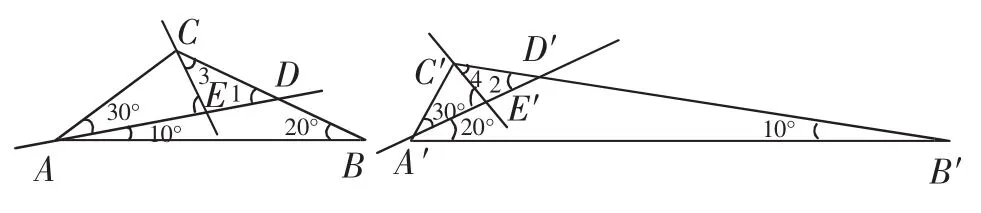
图12

生14：如图12，在探究2中A组分割的基础上再作直线CE和C′E′，使得∠3=∠4，即可得到三对三角形分别对应相似，它们分别是：△ABD与△A′B′D′、△CDE与△C′D′E′、△ACE与△A′C′E′.

师：此时△ACE与△A′C′E′为什么相似？

生15：∠CAE=∠C′A′E′，∠ACE=∠A′C′E′.

师：有道理，请大家接着探究下面的问题.

点评：学生在探究2的基础上，进一步对△ACD与△A′C′D′进行分割，设置了合理的探究台阶，让学生拾级而上，能增强学生的信心，体验成功的快乐，也为后面的进一步探究再做铺垫.

探究5：如果两个钝角三角形中∠C≠∠C′（如图13），能否分别用两条直线分割这两个三角形，使得被分割成的三对三角形分别对应相似？

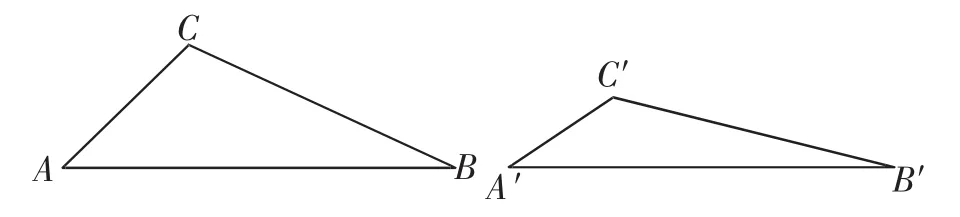
图13

师：为了便于分割，我们可以先假设两个三角形各内角的度数.

生16：设∠C=110°、∠C′=125°，同时令∠A=40°、∠B=30°、∠A′=35°、∠B′=20°.

师：请大家首先在两个三角形中分割出一对相似三角形.

生17：用“割大出小”的思路，在∠A中割出20°角，在∠A′中割出30°角，使得△ABD与△A′B′D′相似（如图14）.

图14

师（追问）：接着怎么分割？

生17：剩下的问题就是在△ACD和△A′C′D′中进行分割，由于这两个三角形中有∠CDA=∠C′D′A′=50°，所以剩下的问题就是我们熟悉的问题，用结论1即可解决.

师：具体怎么解决？请大家在导学案上画出分割线.

生18：如图14，在△ACD和△A′C′D′中，因为20°+110°=5°+125°，所以20°-5°=125°-110°，即在∠CAD中分割出5°角，在∠A′C′D′中分割出110°角，此时△ACE与△A′C′E′、△ADE与△C′D′E′相似，结合前面得到的△ABD与△A′B′D′相似，共有三对三角形相似.

师：请大家归纳一下分割的思路.

生19：主要分两步，第一步，分别找两个三角形中的最小角，以“你中有我、我中有你”的方式进行分割，构造出一对相似三角形和另一对只有一组角相等的三角形；第二步，在只有一组角相等的三角形中运用结论1再分割即可.

师：由上面的5个探究，你能归纳出什么结论？说给小组其他成员听听.（给学生充分的时间，学生归纳的同时，老师边补充边板书）

结论2：任意两个不相似的三角形都可分别用两条直线分割，使分割得到的三对三角形分别对应相似.

师：现在我们能不能解决课前提出的花圃问题？

生（齐）：能.

探究6：校园内有一块等腰直角三角形和一块正三角形的空地，现打算把它们分别种植成三种不同颜色的花圃，且使得每种颜色的花圃所形成的图形为相似的三角形，你能帮忙设计一下吗？

部分学生作品展示：

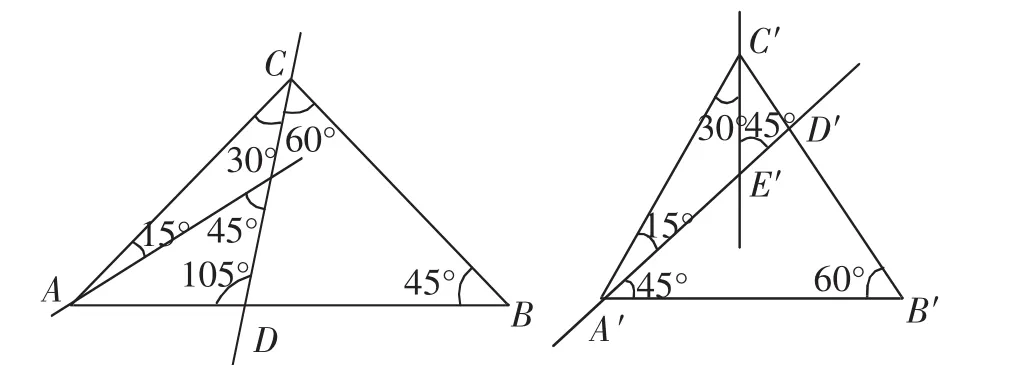
图15

点评：经历了前面循序渐进、步步深入的探究和结论1、结论2的归纳，学生已经基本掌握了分割图形的方法，对于花圃问题的解决自然水到渠成.

师：在课本原题中，两直角相等，我们不仅可以看成相等，还可以看成互补，对不对？

生（齐）：对.

师：请问，如果两个三角形有一对角互补，我们是否可以分别用一条直线把它分割成两个三角形，使所得的两对三角形分别对应相似？如果能，你还能归纳出什么结论？请大家课后继续钻研，将探究进行到底！

三、教学内容的简略分析

数学探究，是一种发现式学习，是让学生在数学学习的情境中，通过观察、操作，发现问题，形成解释并获得答案，从而发现一些数学的规律.在本课例中，教者的任务就是激发和调动学生的探究欲望，使学生一直处于一种积极探究的冲动之中.

在设计问题情境时，笔者给出两条探究线索.一是指导学生学的明线：即“校园里有两个三角形空地，要分割成三对对应相似的三色花圃，如何分割？”在教学设计上，先提出这一问题，并最终解决这一问题，步步深入、环环相扣、指向鲜明；二是指导教师教的暗线：“原教材八年级下册P123第15题”，它既是本节课探究教学的源头，又是教材给出的一个通过探索研究需要解决的问题.

在实施探究活动时，笔者又设计两大探究板块.一是有条件分割出两对三角形相似得出结论1，二是无条件分割出三对三角形相似得出结论2.两大探究板块，阶梯式设计若干可探问题，层层深入地让学生在自主合作探究中享受问题解决的乐趣.在结论1的探究板块，为激发学生探究的兴趣，增强学生探究的信心，关注学生对问题的思考，笔者设计了分割花圃、相似判定、问题探究、构建模型四个环节，让学生在合作探究的基础上得出结论1.为得出结论2，先在钝角相等的两钝角三角形中，提出用两条线分割，得到三对三角形相似，让学生从分得两对三角形相似，到分得三对三角形相似，实施简单的辩证思维训练，然后对两钝角三角形中钝角不相等，提出用两条线分割得三对三角形相似，引导学生实施步步转化的策略解决问题.在探究过程中，不仅得出结论2，而且还引导学生通过探究掌握了分割图形的方法.

另外，结论1、2的得出，都是用“分不等角”的办法来实施的.可能会有同学提出这样的疑问，如果用“分相等角”的办法，我们还会得出什么结论？因此，在本节课最后，笔者布置这样一个作业留给学生课后探究.请问：如果两个三角形有一对角互补，我们是否可以分别用一条直线把它分割成两个三角形，使所得的两对三角形对应相似？学生通过课后的探究，可把结论1拓展成：任意两个不相似的三角形，只要有一对角相等或互补，都可分别用一条直线分割这两个三角形，使所分割得到的两对三角形分别对应相似.

四、教学方法的理论依据

探究教学的思想渊源可以追溯到20世纪初.当时，针对脱离儿童生活经验、纯知识灌输的美国传统教育，著名实用主义教育家杜威提出以儿童为中心、从做中学的主张.笔者理解的初中数学探究，就是以“探索研究”中问题解决为由头，让学生自主体验、探索研究的学习过程，从而培养学生的创新精神和实践能力.如果说创新是有点空的，探究就是实的.对数学学科而言，图形的研究、定理的得出、问题的展开，都是很好的探究载体.按照笔者提出的三维数学思想的理念，学生“学会”数学知识都是暂时、被动和有限的，而“会学”数学知识才是长远、主动和无限的，通过“数学探究”促使学生会学习，才是教育的根本目的.

从“课标”所提出的培养学生发现和提出问题、分析和解决问题的能力来讲，数学探究贯穿于发现、提出、分析和解决问题的整个过程当中，没有“数学探究”就没有“问题解决”，更没有广泛深刻的“数学思考”.数学探究，既是目的，更是手段.通过数学探究，我们不仅可以对教材中“探索研究”问题有一定认识，更重要的是在问题解决的过程中提升学生的学习能力.笔者还想就教学中彰显的三维数学思想中的“三思学习法”做一点解释.一是“建模的思想”.要提升自己的探究能力，就必须对所探究的问题，构建一定的数学模型.本节课结论1、2的得出，以及解决问题的方法的总结，给人以清晰的数学模型，让学生感觉到数学模型的建构，不是高不可攀，而是触手可及.二是“辩证的思维”.辩证的观点是智慧的象征，学力的提升依赖辩证的思维.本课例中的探究由特殊三角形到一般三角形，由有相等角到没有相等角，由分割少到分割多，这些都是辩证思维的结晶.三是“化归的思路”.数学问题的解决过程，就是问题转化的过程，学力的提升都融合在问题转化的过程中.本课例探究的终极目标，就是导学线索中花圃分割的问题，其解决的过程就是将分割得三对三角形相似的问题先化归成两对，进而再使用结论1转化成三对.可以这样说，三思学习法是我们在数学探究中提升学力的重要方法.

五、随感随想

数学探究是一种“主动”的学习方式，实践证明，它有助于学生初步理解结论产生的过程，体验创造的激情，建立严谨的科学态度和不怕困难的科学精神.事实上，我们应该注意到，在教材中，不仅章节最后的“探索研究”是数学探究的良田，而且在数学问题呈现的过程中，教材中所没有的若干“探索”问题，也是数学探究的沃土.

在实际教学中，要完成正常的教学任务，老师们很少有时间对教材中的“探索研究”问题进行剖析与延伸.但是，我们完全可以在一段时间内，搞一两个这样的示范，筛选一些学生感兴趣的问题来探究，让学生在探究的过程中，觉得数学好玩、数学很有意思.当然，一个成熟的探究问题，必定是教者专心研究的成果，为提高数学探究的质量，教者必须先行研究，致力于提升自己的修为，不断追求问题解决的最高境界.每个孩子都是有待开采的“金矿”，教者要努力把本领显在学生潜能的充分挖掘上.要努力把内功下到对探究问题的深度掌控中，体现教师的主导作用.更为重要的是，学生是主体，精心预设的目的，是要构建一个灵活的生成空间，以最大化激发学生的生命活力和智慧的潜力，要相信学生的潜能，坚信给他们一个机会，学生一定会还我们一个奇迹！所以，兴趣是老师，教师是主导，学生是主体.

需要说明的是，本节课对最后一个引发继续探究思考的铺垫做得还不够，留给学生思考的空间不足.通过这节课的录制，以及近年来的教学研究，笔者有一个强烈的感受，探究问题不能满足于几节课，应把探究贯穿于学习的始终，甚至学生学习的一生.如何生成学生的“数学探究”空间，对于我们数学教师来说，任重而道远.

1.喻平.著名特级教师教学思想录［M］.南京：江苏教育出版社，2012.

2.曹才翰，章建跃.中学数学教学概论［M］.北京：北京师范大学出版社，2008.

3.涂荣豹，季素月.数学课程与教学论新编［M］.南京：江苏教育出版社，2007.