解读苏科版数学教材中“数轴”的意义

☉江苏省宿迁市宿豫区教育局教研室 胡 滨

解读苏科版数学教材中“数轴”的意义

☉江苏省宿迁市宿豫区教育局教研室 胡 滨

关于数轴的意义，义务教育数学课程标准（2011年版）没有提出明确的教学要求，只是提出“能用数轴表示……”与“借助数轴理解……”等用数轴解决问题的一些具体要求.那么在教学过程中，数轴概念意义的形成与获得过程是否就应该“弱化”处理呢？其实不然，经教育部审定后的最新苏科版义务教育教科书七年级（上册）中的《2.3数轴》教材中，数轴意义的内容呈现比修订前更加细化、深化、强化了许多环节与内容.对此，我们解读如下.

一、细化数轴意义的引入内容，突出数学基本观念的把握

试一试（摘自原教材）：

在小学里，我们会根据直线上一个点的位置写出合适的数，也会在直线上画出表示一个数的点.

试把图1中直线上的点所表示的数写在相应的方框里.

图1

这里的“试一试”有两个作用，一是回顾经验，二是激活经验.因为我们的一切知识都是建立在经验之上，而且最后是导源于经验的.在已有的小学数学经验上，我们认识到的数学对象有：根据直线上的一个点的位置写出合适的数；这种直线上的点是依次排列的；可以在直线上画出表示一个数的点；这样的直线帮助我们认识自然数的大小关系.当借助数学经验感知这些有一定层次的数学对象时，三个数学基本观念——“直线”、“点”、“数”就随即直观地传达于我们心中.再深入反思这三个基本观念时，我们便获得了清晰的“数轴”初步概念意义的层次：

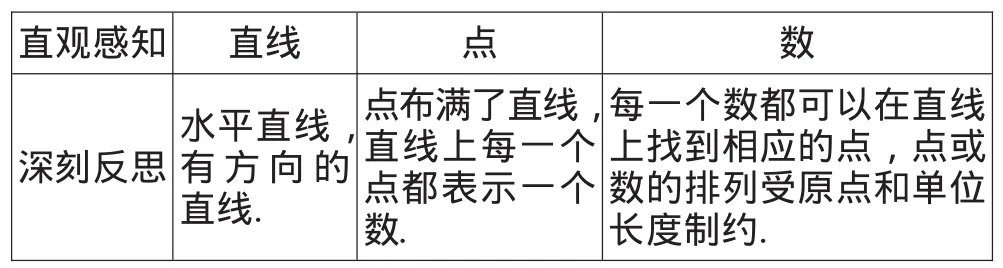
直观感知 直线 点 数深刻反思水平直线，有方向的直线.点布满了直线，直线上每一个点都表示一个数.每一个数都可以在直线上找到相应的点，点或数的排列受原点和单位长度制约.

所以，在这里的“试一试”数学活动过程中，回顾已有数学经验是认识数轴的基础，感知数学对象、获得基本观念是数轴概念形成的核心，深刻反思是形成清晰数轴概念层次的关键.可以说，数轴概念的形成，得益于能从已有的数学经验中获得三个数学基本观念——“直线”、“点”、“数”，直观感知与深刻的心理活动是数学基本观念形成的两个重要途径.因此，引入教材内容教学的重点在于，首先能从已有数学基本经验中提炼出基本数学观念，其次是能够深入思考、记忆、整理与使用这些基本观念，使得“数”在“形”上呈现出可见对象与直观支撑，最后才能形成完整的数轴概念图式.这就启示我们的教学设计应当关注以下几点：

1.由于图形的实质是将相对抽象的“数”的思考对象“图形化”，因此在激活小学数学经验时，能画图时要尽量安排学生画.

2.刚刚进入初中学习的小学生往往都把注意力消耗在观察图形（图1）上，很少能仔细反省心中对数学对象的感知、以及对数学观念的剖析上，要加强学习方面的引导与针对性的知识小结.

3.给学生做出“数学书应该这样阅读”的示范.即能理解数学对象、数学观念、数学方法、数学经验事实的精确含义，特别是隐藏在文字背后的含义，能善于在课文内容的字里行间中发现问题，并就这些问题的提出、分析、抽象、解决和引申作适当的探索.

二、深化数轴概念的表述，突出数轴的“表示”要义

在数轴上，我们看到了“点”可以表示“数”，如“数轴”上的点可以表示数-1，-2，-3，…可以表示数0，可以表示数1，2，3，…可以表示数-2.5，3.5，-1.5，-，，…这说明两个道理，一是凡能写成分数形式（m、n是整数，n≠0）的数，都在数轴上；二是数轴上表示有理数的点有“很多”.例如，数轴上两点A、B，它们所对应的数分别是a、b，那么A、B的中点所对应的数值是，同理可以知道其他两点的中点所对应的数值，这样继续找下去，虽然距离越来越小，但每两点之间总有一个中点，而且这个中点所对应的数值可以计算出来，它也可以是分数形式.显而易见，这些点是很稠密的排列在数轴上.

“数轴”上“点”与“数”的关系是相互对应的.这种对应表现为一种意识——面对数学问题能想到利用图形来思考；其次表现为掌握一定的几何直观的画图技巧，能画出数轴并借助数轴图形进行思考的经历和经验，表现为一种能力；想不想画出数轴、会不会画数轴图的问

做一做（摘自原教材）：

1.画一条水平直线，并在这条直线上取一点表示0，我们把这个点称为原点.

2.规定直线上从原点向右为正方向（画箭头表示），向左为负方向.

3.取适当长度（如1cm）为单位长度，在直线上，从原点向右每隔一个单位长度取一点，依次表示1，2，3，…从原点向左每隔一个单位长度取一点，依次表示-1，-2，-3，…

如图2，像这样规定了原点、正方向和单位长度的直线叫做数轴.

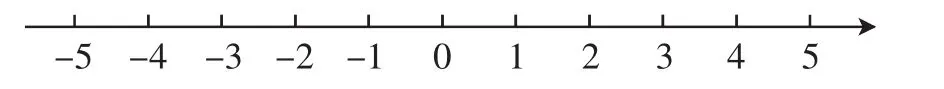
图2

在数轴上，用原点右边且到原点的距离是1.5个单位长度的点表示1.5，用原点左边且到原点的距离是2.4个单位长度的点表示-2.4.

通过具体的“做一做”，得到了“像这样规定了原点、正方向和单位长度的直线叫做数轴”的带有操作程序性的意义.当你接受数轴意义内容就是数轴的三要素——原点、正方向、单位长度时，后来关于数轴的一切观念，就会永远建立在这个基础上，至于对数轴意义的深刻理解，则可能是被动的.人类理解理论相关研究指出，人类智力的第一种能力，就在于接受印象，然而就在接受简单的观念时，大部分理解是被动的.因此，若想得到数轴的深刻意义，必须借助已经接受的简单观念来增进自己的思想能力，以增加自己的知识储备，以便使自己在回忆、想象、推理和思考时，更能顺利地使用数轴的意义图式.

“数轴”的意义与“直线、点、数”三个数学观念是相符合的，它的基本特征就是依托、利用图形进行数学思考和想象.先把研究的“数”抽象为“图形（点）”，再把“直线、点、数三个数学观念之间的关系”转化为“数与形之间的关系”，这样就把研究“数”的问题转化为“图形的数量或位置关系”的问题，加以思考分析.这就是说，数轴知识是直觉的知识，直觉知识是最明白、最确定的，这种确定性完全依赖于直觉.因此，不需要记住它的什么意义、什么三要素，只要求能切实感知到它的直观，深刻反思它的意义，灵活使用它来解决数学问题.

在这一段课文内容中，出现频率最高的词就是“表示”，就是说，数轴的重要作用在于“表示”.“表示”有“表述、表明、标记、借某种事物显出某种意义”等含义，因此，把握数轴意义的重点在于，借助数轴的“表示”作用不仅能直接看到想要知道的东西，而且还能依托看到的东西进行思考、想象，即不仅看到了什么，而是通过数轴思考到了什么，联想到了什么.这是一种十分重要而有价值的思维方式.题解决之后，不断地运用，形成正向的动力定型，逐步会形成一种当遇到抽象理性的问题时，主动地退到适合的层面上去推动思维展开的思维方式.

要使得在具体的教学环节设计上产生预想的教学效果，应当关注以下几点：

1.准确完成数轴的画图，既知道画数轴的方法，更有娴熟画数轴的技能.

2.在数轴上能领悟到数的对立统一规律与数的排列规律.

3.欣赏数轴的和谐美，它把直线、射线、线段有机统一于一体，使有理数与无理数共存于其中，体现了数与形的完美结合.

三、强化无理数的引入过程，突出几何直观的重要作用

议一议（摘自原教材）：

面积为2的正方形的边长a是无理数，如何在数轴上画出表示a的点？

以原点为一个端点，在数轴上向右画一条长为a的线段.

a应位于1.41与1.42之间.

做一做：

将边长为a的正方形放到数轴上（如图3），以原点为圆心、a为半径，用圆规画出数轴上的一个点A，点A表示的数就是无理数.

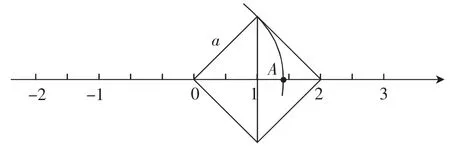
图3

怎样用数轴上的点表示圆周率π？

做一个直径为1个单位长度的圆片，它的周长为

如图4，把圆片上的点放在原点，并把圆片沿数轴滚动1周，点A到达点A′的位置，点A′表示的数就是π.

图4

议一议、做一做两段教材内容揭示了“数轴”与“实数”的关系，其主要内容有：

“数轴”上表示有理数的点，并未布满整个数轴.数轴上的点还可以表示哪些数呢？如图3中的点A和图4中的圆周率π，它们都是无理数.我们若参照图3，还可以构造出对角线长分别为1，1.5，3，3.5，…无数个正方形来，它们的边长都是无理数，都可以在数轴上找到相对应的点来表示.就是说，数轴上表示无理数的点也有“很多”，它和有理数一起共同布满了整个数轴.正如课文内容所表述的那样：有理数和无理数都可以用数轴上的点表示；反过来，数轴上的任意一点都表示一个有理数或无理数.

“数轴”上并非有理数“多于”无理数.我们若以任一有理点为起点，向右移动与以单位长为边所作的正方形对角线等长的距离，就可以得到和所有有理点“一样多”的无理点.但是，我们还可以找出任意多的其他无理点，如以1与2分别为长和宽作一个矩形，其对角线的长为距离的点就是一个无理点，这样的点还可以按照这种办法找出很多.每找出这样一个无理点，又可以再产生与有理点“一样多”的无理点.这就是说，在数轴上，并非有理数“多于”无理数.

“数轴”上的点可以表示的数有两类：一类是可以写成分数形式的有理数，另一类是形如图3中的点A与图4中的圆周率π所表示的无理数，即数轴上点可以表示有理数和无理数，表示有理数的点是稠密的，表述无理数的点也是稠密的，它们共同布满了整个数轴.至此，有关“实数”意义的基本观念已十分清晰地呈现在我们的面前.对这段教材内容的分析，启示我们的教学设计应关注这样几点：

1.计算无理数值的一般思想，是用有理数逐步逼近的.

2.从有理数出发，用作图的方法可以得到庞大的无理数家族.有一个无理数a，就可以造出无穷多个无理数来，如2a，a+2等；有一个无理数π，同样可以造出无穷多个无理数来.这些无理数不过是庞大无理数家族中小小的一支而已.

3.用“作图”的方法在数轴上找到表示无理数的点，表明两层意思：一是这种“实验”是在想象中做的、是设想着做的、是在思想中进行的实验，在数学中，我们常常使用思想实验；二是这样的点只是示意性的，其示意性突出表现在无理数形成的内在机理的数量关系，随着学习不断深入，我们会逐渐明白这种示意图的准确意义.

1.杨裕前，董林伟.义务教育教科书数学·七年级上册［M］.南京：江苏科学技术出版社，2013.

2.王国生，张强.中学数学里的数轴［J］.数学通报，1957（2）.

3.［英］洛克.人类理解论［M］.北京：商务印书馆，2012.