改进非支配排序进化算法在下料问题中的应用

阚方，刘林，2，方昶，裴军，郑明月

KAN Fang1,LIU Lin1，2,FANG Chang1,PEI Jun1,ZHENG Mingyue1

1.合肥工业大学管理学院，合肥230009

2.合肥工业大学管理学院过程优化与智能决策教育部重点实验室，合肥230009

1.School of Management,Hefei University of Technology,Hefei 230009,China

2.Key Laboratory of Process Optimization and Intelligent Decision-making,Ministry of Education,School of Management,Hefei University of Technology,Hefei 230009,China

1 引言

一维下料问题是一个在企业生产过程中普遍存在的问题，有效的下料方法可以使企业按照最优的方式切割，提升企业的经济效益。近年来，随着各种新的优化算法的提出，对于一维下料问题的研究也越来越深入，例如，文献[1]将顺序启发式算法和分支定界法相结合；文献[2]提出并实现了非定长优化和定长优化相结合的两阶段优化的下料方法；当问题规模大到一定程度时，一些元启发式算法得到了应用，文献[3]引入变异操作对蚁群算法进行改进；文献[4]提出了一种多级混合式启发算法MHA（Mixed Heuristic Algorithm）；文献[5]提出的模拟退火算法、文献[6]提出的一种多目标的改进禁忌搜索算法等都是这方面的研究成果；近两年的研究还倾向于采用多种方法复合[7-10]。以上的研究成果多是以算法改进为研究目标，而在实际生产中更迫切地需要考虑原料使用与加工及余料回收的整体优化问题，本文以马钢车轮公司的优化下料决策系统的研究为背景，以减少废料、减少下料设置时间和减少可回收余料为优化目标，通过一种改进的快速非支配排序进化算法和多属性决策方法构建适用于多目标优化下料问题的算法并将其应用于实际中的生产优化。

2 下料模型

马钢车轮公司车轮、轮箍生产过程的第一道工序是将原材料切割成料坯，再进行加热、轧制成型和机械加工。为了提高原材料的利用率，切割必须按一定的优化方案进行。本文假定原料等长、数量充足，且不同下料方式间的切换时间是相等的，确定了以下三个优化目标并建立数学模型：

xij≥0，且为整数，∀i，j；βi≥0，且为整数，∀i；T≥0；Li≥0。

参数定义：N表示待切坯料的种数；M表示下料方案中包含的下料方式数；L表示原料的长度；lj表示第j种坯料的长度；j=1，2，…，N；Lmin表示可收回再利用的余料的最小长度；Li表示在第i个下料方式下配切一根原料所产生的余料长度；i=1，2，…，M；λi表示按第i个下料方式产生的余料是否可再利用（如果Li≥Lmin，则λi=1；否则λi=0）；βi表示按第i个下料方式重复下料的次数；qj表示第j种坯料的需要量；xij表示第i个下料方式中配切第j种坯料的数目；T表示下料方式间切换的单位时间。

式（1）为目标函数，3个目标分别是：（1）不可再利用的余料（浪费）最少；（2）下料切割时，下料方式的设置时间（加工成本）最少（原因是不同下料方式之间切换时，需要对刀具等重新进行设置）；（3）可回收再利用的余料最少（原因是回收需要增加运输和库存费用）；式（2）为原料长度约束；式（3）为坯料的需求约束。

3 一维下料决策过程

3.1 算法

3.1.1 编码方法

用pi=(ai1，ai2，…，aij，…，aiN)表示第i种下料方式，其中aij表示在第i种下料方式中切第j种坯料的数目。例如有待切坯料6种，下料方式（2，1，0，3，2，1）就表示在原料上切2个1号坯料，1个2号坯料，0个3号坯料，3个4号坯料，2个5号坯料和1个6号坯料。

再用βi表示需要用第i种下料方式的重复使用次数（即所用原料的根数），则下料方案S就可表示为：S={p1*β1，p2*β2，…，pi*βi，…}。

3.1.2 初始种群

因为刀缝宽度是事先确定的，本文设计下料时将刀缝宽度加在坯料长度上，以简化计算。按照下面方法生成下料方式，直到坯料的需求都被满足，即形成一个下料方案。具体步骤如下：

步骤1初始化：将待切割的坯料放入集合π1中；

步骤2取一根原料L，从π1中随机选择一种坯料，在满足L够用和不超过该种坯料需求量的前提下随机生成一个整数xj作为在该下料方式中该个坯料将要配切的数目。更新原料的剩余长度L′，从π1中再次随机选择长度小于L′的坯料进行配切，重复上述步骤直至L′不可再用，判断L′不可用后需要考虑一种特殊情况，即L′和π1中减去刀缝宽度的某种坯料lx长度一致，则配切一个lx（因为此时所剩的余料正好被利用，不再产生刀缝宽度）。即得到第一个下料方式p1，将p1重复下料β1次，（K为此下料方式中所配切的坯料种数，qj为此下料方式中第j种坯料此时的剩余需求量，xj为此下料方式中配切第j种坯料的个数，为下取整函数），更新π1中还有需求量的坯料，将qj≤∂j的坯料从π1中取出，放入集合π3中，∂j=[L/lj]，j=1，2，…，N。其中[]为取整函数，该式表示每种坯料最多可在一根原料上切割的数目，当坯料的需求量小于或等于其对应的∂值时，该种坯料就有可能在一根原料上切割以达到需求量，这会大大增加下料方式数。

步骤3取原料L，将π1中的坯料放入集合π2中，取出长度最大的坯料lmax进行配切（因为最长的坯料较难与其他坯料进行组合配切，故优先考虑），配切的数量记为xmax，在满足xmax小于或等于该坯料的需求量的前提下，使xmaxlmax≤L＜(xmax+1)lmax。更新π1中还有需求量的坯料，将qj≤∂j的坯料从π1中取出，放入集合π3中，判断π1是否为空，如果为空，转步骤5，如果不为空，继续下一步。

步骤4更新原料的剩余长度L′，（1）若L′小于π2中最小长度的坯料，结束配切（判断时仍需考虑步骤2提到的特殊情况），即生成下料方式pi，将pi重复下料。（2）若L′大于π2中最小长度的坯料，把π2中的坯料按需求量进行降序排序（如果需求量一样，则按坯料的长度降序排列），其对应的坯料长度分别为lm，lm-1，…，l1。从lm开始和已配切的坯料进行组合配切（因为需求量较大的坯料优先配切可以有效减少下料方式数，需求量一样时较长的坯料较难与其他坯料进行组合配切，故优先考虑），在满足xm小于或等于该坯料的需求量的前提下，使xmlm≤L′＜xm+1lm，其中xm≥0。更新π1中还有需求量的坯料，将qj≤∂j的坯料从π1中取出，放入集合π3中，将配切过的坯料从π2中除去，如果π1、π2都不为空，返回步骤4；如果π2为空且π1不为空，输出下料方式pi=xmaxlmax+xmlm+xm-1lm-1…，将pi重复下料βi次，2，…，K)，返回步骤3；如果π1为空，转步骤5。

步骤5将π3中的坯料按上述算法配切生成下料方式，直至π3为空。输出下料方案，结束算法。

初始种群算法如图1所示。

图1 初始种群生成方法

3.1.3 快速非支配排序和拥挤度计算

采用文献[11]的方法对种群进行快速非支配排序并计算个体的拥挤度，这时种群中的每个个体i都得到非支配排序等级和拥挤度这两个属性。如果两个个体的非支配排序等级不同时，优先选择等级低的个体；如果两个个体的非支配排序等级相同，优先选择拥挤度较低的个体。用选出的个体构造新群体。

3.1.4 进化算子

步骤1对于生成的每个下料方案，将其中的下料方式按值由大到小排列，比例相等的按余料长度由小到大排列（式中Δ为一个较小的正数，目的是为了防止分母为0）。

步骤2对于按步骤1排序完成的一个下料方案，随机生成一个基因位。保持该基因位及其前面的基因不变，把该基因位后面的基因删除，将删除的基因数据还原成待配切的坯料数据。

步骤3对还原成待配切的坯料，运行上述的算法，重新生成新的下料方式，将相同的下料方式合并。

3.1.5 精英策略

为避免进化过程中优良个体的丢失，提高优化结果的精度，将父代种群与所产生的子代种群合并，共同竞争产生新一代种群。

3.1.6 算法整体流程

步骤1初始化，生成规模为Npop的初始种群P。

步骤2执行进化算子，产生规模为Npop的子代种群Q。

步骤3将P与Q合并，计算合并后的种群中个体的多目标适应值。

步骤4对合并后的种群进行快速非支配排序，确定Pareto解集的层次{F1，F2，F3，…}。

步骤5计算个体的拥挤度。

步骤6执行拥挤选择操作，产生规模为Npop的新父代种群P。

步骤7判断终止条件是否满足（是否达到迭代次数），如果满足，结束算法，输出Pareto最优解集，否则返回步骤2。

3.2 基于理想点法的多目标下料决策

通过以上算法得到一个Pareto解集，决策者还面临如何从这个解集的多个解中选出满意方案的问题。在这里将解集当作备选方案集F={f1，f2，…，fm}，为了消除各指标间的不可公度性以及统一各指标的趋势，在进行评价前对其进行规范化处理；将优化目标集作为评价属性集Z={z1，z2，z3}，运用CRITIC法[12]计算客观权重；最后用逼近理想解法选出一个满意解作为下料方案。

4 算例

本文用提出的算法对随机产生的实例进行了实验测试，算法使用Delphi 7语言编程，在英特尔奔腾2.4 GHz处理器上运行。下料所使用的原料钢锭长度L=2 000 mm，可再利用余料的最小长度设为当前下料规模中坯料长度最小值，下料方式间的切换时间为20 min，进化算法的种群规模取2N，进化代数为100，各坯料的长度和需求量如表1所示。本文实验设计分别对不同坯料规模的下料问题进行运算，10种下料规模为a1～a10，20种下料规模为a1～a20，以此类推，算法运行结果如表2所示。

表1 坯料重量与需求量

表2 算法运行结果

图2显示了下料规模为30时，Parteo最优解对应的个体数在群体中所占比例在迭代过程中的变化情况。本文设定的迭代次数为100，由图可知实际运行到40代左右时，Parteo最优解对应的个体数已基本保持不变，收敛速度较快，运行到100代时，Parteo最优解的个数为17。

图2 Pareto解集中解的个数所占比例

表3显示了下料规模为30时，运行该算法求出的Parteo最优解集，其中的11号下料方案为运用多属性决策方法选出的最终下料方案；图3显示了未运行算法前的初始种群的解空间分布；图4显示了初始种群经过100次迭代后，Pareto最优解集的分布（即表3中的17个下料方案的分布），通过比较可以发现，该算法具有良好的优化效果。f1表示废料（值均经过归一化处理）；f2表示下料设置时间（值均经过归一化处理）；f3表示返回余料根数（值均经过归一化处理）。

表3 Pareto最优解集

5 结束语

（1）本文研究的是多目标一维下料问题，建立了减少废料、减少下料设置时间和减少可回收余料三个目标的优化下料模型，针对该问题的特点，设计了一种多目标启发式进化算法来求Pareto解集，再采用多属性决策方法对Pareto解集中的解进行评估排序，以获取满意的下料决策方案。

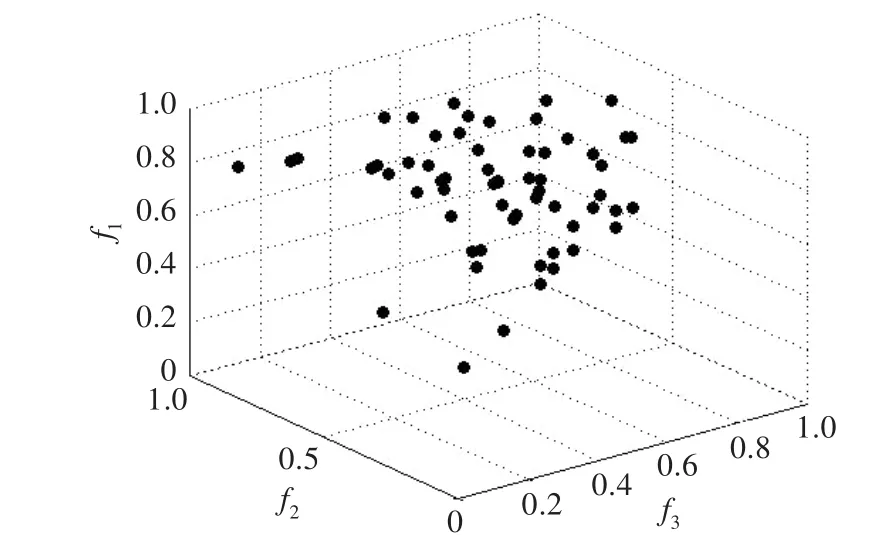
图3 初始种群的解空间分布情况

图4 迭代100次后Pareto最优解集的分布情况

（2）实验结果表明，本文算法对中等规模的下料问题是可行有效的，在种群规模合适的情况下，其迭代次数和所用时间是较优的，且保证了较高的原料利用率，运用多目标优化和多属性决策相结合的方法可以有效地解决多目标下料的决策问题。

（3）此方法现已被应用于马钢车轮公司的下料决策系统，与公司原来使用的下料系统相比，不仅可以提高钢材的利用率，缩减编制下料方案的工作时间，而且还大大简化了下料决策过程和复杂程度。但随着下料规模的持续扩大，如何提高该算法的优化质量和运行时间，是需要进一步研究的课题。

[1] Gradisar M，Trkman P.A combined approach to the solution to the general one-dimensional cutting stock problem[J].ComputersandOperationsResearch，2005，32：1793-1807.

[2] 阎春平，宋天峰，刘飞.面向可制造性的两阶段一维下料优化下料方法[J].计算机辅助设计与图形学学报，2009，21（12）：1785-1790.

[3] Lu Qiang，Wang Zhiguang，Chen Ming.An ant colony optimization algorithm for the one-dimensional cutting stock problem with multiple stock lengths[C]//Fourth International Conference on Natural Computation，ICNC’08，2008：475-479.

[4] Huo Yingyu，He Kejing，Zhang Rengui，et al.MHA：a mixed heuristic algorithm for the cutting stock problem[C]//International Conference on Information and Automation，ICIA’09，2009：460-465.

[5] Chen Chuen-Lung，Hart S M，Tham W M.A simulated annealing heuristic for the one dimensional cutting stock problem[J].European Journal of Operation Research，1995，32：522-535.

[6] Yang C T，Sung T C，Weng W C.An improved tabu search approach with mixed objective function for one-dimensional cutting stock problems[J].Advances in Engineering Software，2006，37：502-513.

[7] Gradisar M，Resinovic G，Kljajic M.A hybrid approach for optimization of one-dimensional cutting[J].European Journal of Operational Research，1999，119（3）：719-728.

[8] Vasko F J，Newhart D D，Kenneth L，et al.A hierarchical approach for one-dimensional cutting stock problems in the steelindustry that maximizes yield and minimizes overgrading[J].European Journal of Operational Research，1999，114（1）：72-82.

[9] Paolo T.Optimization engineering techniques for exact solution of NP-hard combinatorial optimization problems[J].European Journal of Operational Research，2000，125（2）：222-238.

[10] 包奇金宝，姜静清，宋初一，等.基于粒子群与模拟退火算法的板材优化下料[J].计算机工程与应用，2008，44（26）：246-248.

[11] Deb K，Pratap A，Agrawal S，et al.A fast and elitist multi objective genetic algorithm：NSGA II[J].IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197.

[12] Diakoulaki D，Mavrotas G，Papayannakis L.Determining objective weights in multiple criteria problem：the CRITIC method[J].Computers and Operations Research，1995，22：763-770.