一类带阶段结构的捕食-食饵扩散系统的稳定性

曹怀火，李海燕，张永2，

CAO Huaihuo1，3,LI Haiyan3,ZHANG Yong2，3

1.陕西师范大学数学与信息科学学院，西安710062

2.兰州大学数学与统计学院，兰州730000

3.池州学院数学与计算机科学系，安徽池州247100

1.School of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China

2.School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,China

3.Department of Mathematics and Computer Science,Chizhou University,Chizhou,Anhui 247100,China

1 引言

文献[1]讨论了三次捕食者-食饵扩散系统：

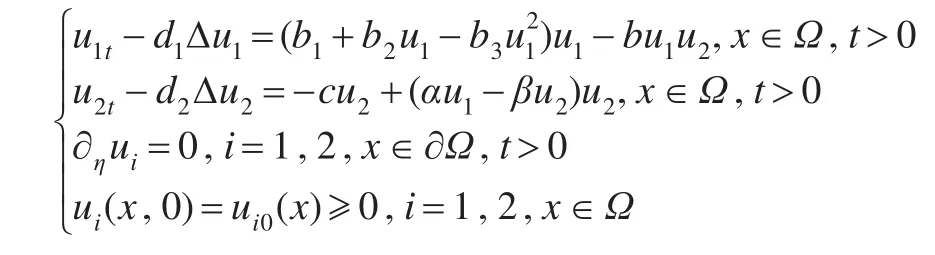
解的整体性态，其中Ω是Rn(n≥1)中具有光滑边界的有界区域，∂η=∂/∂η，η是∂Ω上的单位外法向量，u1(x，t)，u2(x，t)分别是食饵种群和捕食者种群的密度函数，扩散系数d1，d2及生命系数b3，b4，c，α，β都是正常数，b1非负，b2的符号不定，b1表示食饵种群的内禀增长率，c是捕食者的净死亡率，捕食者的生存依赖于食饵的生存状况，b2u1-b3与βu2分别为食饵与捕食者的密度制约项，b4u1表示捕食者对食饵的捕食率，αu1表示食饵转化为捕食者自身的增长率，ui0(x)(i=1，2)是非负且不恒为零的光滑函数。最近，文献[2]讨论了简化反应项与边界条件情形下系统：

平衡态正解的存在性。

本文着重研究如下带有阶段结构和空间扩散的三次捕食者-食饵模型：

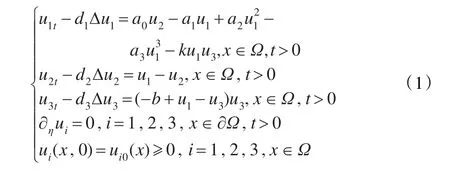
非负平衡解的稳定性，其中u1(x，t)，u2(x，t)分别是食饵种群的幼年种群和成年种群的密度函数，u3(x，t)是捕食者种群的密度函数，扩散系数d1，d2，d3及生命系数a0，a1，a3，k，b都是正常数，a2的符号不定，ui0(x)(i=1，2，3)是非负且不恒为零的光滑函数。模型详细的生态学意义可参见文献[3-9]。

2 平衡点分析

经计算，式（1）有平凡平衡点O(0，0，0)；若a2＞0，，则有半平凡平衡点；若a2≤0，a1-a0＜0；或a2＞0，a1-a0≤0，则有半平凡平衡点：

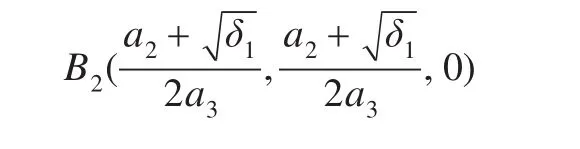
若

或

或

则有唯一正平衡点：

其中δ2=(a2-k)2-4a3(a1-a0-kb)；若

则有两个正平衡点，即

3 一致有界性

本章主要讨论问题式（1）古典解的整体存在性和一致有界性。在建立问题式（1）的解关于时间一致的L∞(Ω)先验估计时文献[10]（Exercise 4 of Section 3.5）起重要作用，下面的定理表明了式（1）的解是整体存在和一致有界的。

定理3.1设(u1(x,t),u2(x,t)，u3(x，t))∈[C(Ωˉ×[0，T))∩C2，1(Ω×(0，T))]3是式（1）具初值ui(x，0)=ui0(x)≥(≠)0(i=1，2，3)的解，其中T是解的最大存在时间，则0＜ui(x，t)≤Mi(i=1，2，3)，t∈(0，T)，其中

证明注意到f1，f2，f3在R3上光滑，初值ui0(x)(i=1，2，3)是非负且不恒为零的光滑函数，由抛物型方程的强极值原理知，ui(x，t)＞0(i=1，2，3)，∀t＞0。

下面将问题式（1）中前两个方程两边分别在Ω上积分后线性组合，得

结合文献[10]（Exercise 4 of Section3.5），得有两个半平凡平衡点，即

又注意到：

则根据比较原理，可得：

显然M1，M2，M3不依赖于T，从而式（1）的解(u1(x，t)，u2(x，t)，u3(x，t))在上是一致有界的，进而整体存在，这就完成了定理3.1的证明。

4 局部稳定性

易知，对相应于反应扩散问题式（1）的常微分系统亦有相应的平衡点。由文献[11]知，其相应的半平凡平衡点B32和正平衡点E32都是不稳定的。注意到常微分系统的解是反应扩散问题式（1）的特解，所以对应常微分系统的不稳定平衡点B32，E32分别是相应反应扩散问题式（1）的不稳定平衡点。

下面首先讨论问题式（1）的正平衡点Ej(j=1，2，31)的局部稳定性。设0=μ1＜μ2＜μ3＜…是齐次Neumann边界条件下算子-Δ在Ω上的特征值，E(μi)是与特征值μi相应的H1(Ω)中的特征子空间。记X=[H1(Ω)]3，Xij={c·φji:c∈R3}，其中{φij;j=1，…，dim E(ui)}是E(μi)的一组正交基[12]，则

系统式（1）在Ej(j=1，2，31)处的线性化方程为ut=Lu。对于任意i≥1，Xi是算子L的不变子空间。λ是算子L在Xi上的特征值当且仅当λ是矩阵-μiD+Fu(Ej)的特征值。而-μiD+Fu(Ej)的特征方程为φi(λ)=λ3+Aiλ2+Biλ+Ci=0，其中

由Routh-Hurwitz准则知，它的每个特征值（记作λi，1，λi，2，λi，3）的实部为负的充要条件是Ai＞0，Ci＞0，Hi＞0，于是有

（1）当a2≤0时，注意到a11，a33＜0，a31＞0，所以它的每个特征值的实部为负的一个明显的充分条件是a11+a0＜0。

（2）当a2＞0时，注意到a11＜0蕴涵于a11+a0＜0，所以它的每个特征值的实部为负的一个明显的充分条件也是a11+a0＜0。

现将Ej(j=2，31)分别代入a11+a0＜0，得

定理4.1（1）设式（2）成立，且同时满足下列条件之一：①则式（1）的唯一正平衡点E2局部渐近稳定。（2）设式（2）成立，且同时满足a2-k＞0，0＜a1-a0-kb＜，则式（1）的正平衡点E31局部渐近稳定。

再讨论问题式（1）的半平凡平衡点Bj(j=1，2，31)的局部稳定性。类似上述方法，系统式（1）在Bj(j=1，2，31)处的线性化方程为：

其中

而-μiD+Fu(Bj)的特征方程为ϕi(λ)=λ3+Aiλ2+Biλ+Ci=0，其中

于是类似地可知，

（1）当a2≤0时，注意到a11＜0，所以它的每个特征值的实部为负的一个明显的充分条件是a11+a0＜0，a33＜0。

（2）当a2＞0时，注意到a11＜0蕴涵于a11+a0＜0，所以它的每个特征值的实部为负的一个明显的充分条件也是a11+a0＜0，a33＜0。

现将Bj(j=2，31)分别代入a11+a0＜0，a33＜0，得综上所述并结合B2，31存在的充要条件，可得结论：

定理4.2（1）若满足下述条件之一：

①a2≤0，a1-a0＜0且式（4）成立；的半平凡平衡点B2局部渐近稳定。

最后讨论问题式（1）的平凡平衡点O(0，0，0)的局部稳定性。类似上述方法，系统式（1）在O(0，0，0)处的线性化方程为ut=Lu，L=DΔ+Fu(O)=DΔ+{aij}，其中

注意到a11＜0，a33＜0，所以它的每个特征值的实部为负的一个明显的充分条件是a11+a0＜0，这等价于a0＜a1，进而有结论：

定理4.3若a0＜a1，则式（1）的平凡平衡点O(0，0，0)局部渐近稳定。

5 全局稳定性

本章通过构造Lyapunov函数讨论问题式（1）的各个平衡点的全局渐近稳定性，为此先引入下述引理（文献[13]引理2.5.3的特殊情形）。

引理5.1设a，b为正常数，φ，ϕ∈C1([a,∞))，ϕ(t)≥0，ϕ有下界。如果ϕ′(t)≤-bϕ(t)，ϕ′(t)≤K(∀t≥a)，K为正常数，则

设(u1，u2，u3)是问题式（1）的唯一正解，由定理3.1知，存在与x∈，t≥0无关的正常数C，使得||ui(·，t)||∞≤C(i=1，2，3)，∀t＞0。由文献[14]中定理A2知，对∀t0＞1有

其中α∈(0，1)，C是与t无关的正常数。

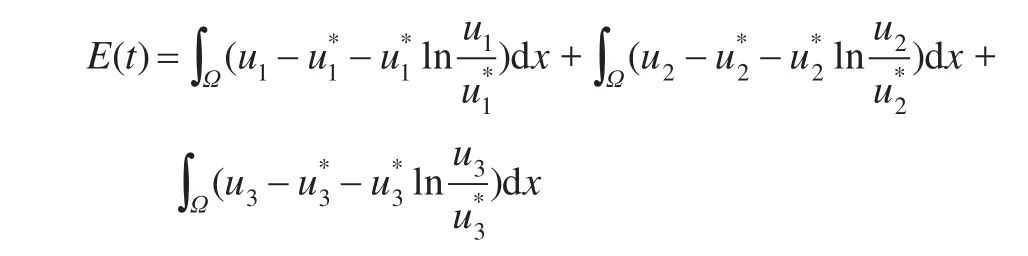
由定理3.1知，在初值取不恒为0的非负函数且t＞0时，问题式（1）的解是严格正函数，故E(t)对式（1）的任意正解有意义。对任意t＞0有E(t)≥0，且E(t)=0当且仅当u=u*。由式（1）得

注意到-a2+＞0等价于：故式（6）成立时，存在正常数，使得又由定理3.1知ui有界，由式（5）知的导数亦有界，从而由引理5.1得

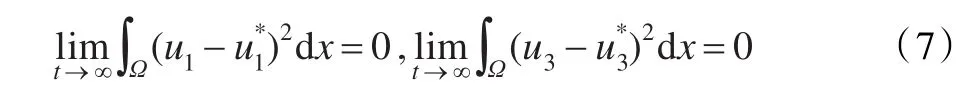
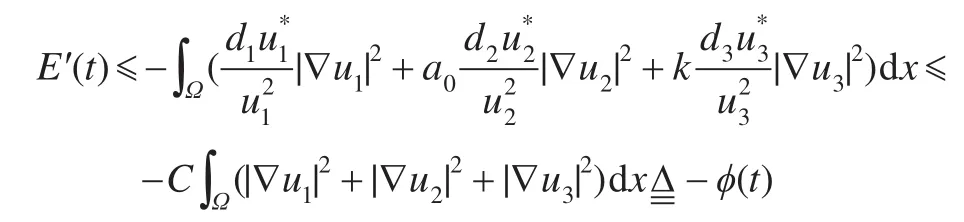
仍由式（5）知ϕ′(t)在[t0，∞)有界，t0＞0。由引理5.1知，当t→∞时ϕ(t)→0，即由Pioncare不等式得：

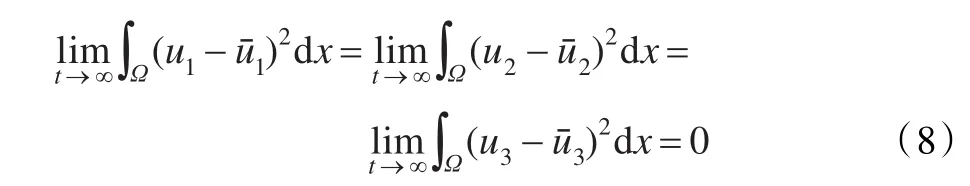
由式（7），（8）得从而存在{tm}，当tm→∞时'(tm)→0。

另一方面：

由式（5）知，存在子列，仍记为{tm}和非负函数ωi∈C2()，使得

定理5.1设式（2），式（6）成立，且同时满足下列条件之一：的正平衡点

则E(t)对式（1）的任意正解有意义。

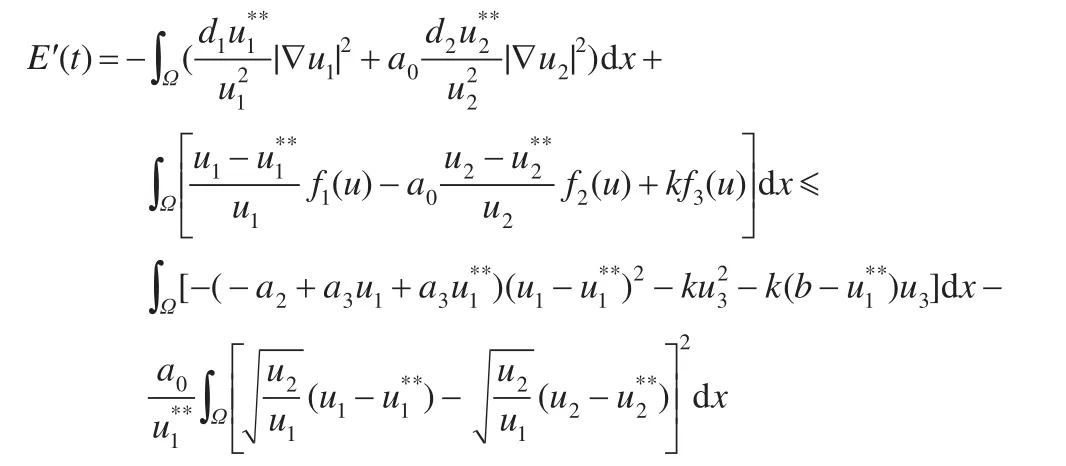
故式（11）成立时，存在正常数：

使得

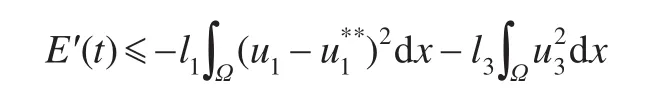
类似于定理5.1的证明，有：

定理5.2（1）设式（4），式（11）成立，且满足下述条件之一：

最后讨论式（1）的平凡平衡点O(0，0，0)的全局渐近稳定性。定义Lyapunov泛函：

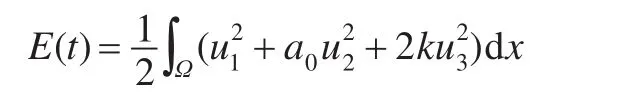
则E(t)对式（1）的任意正解有意义。

注意到a0＜a1，a2≤0时，存在正常数

进而有结论：

定理5.3若a0＜a1，a2≤0，则式（1）的平凡平衡点O(0，0，0)全局渐近稳定。

6 结束语

本文考虑了一类食饵种群带有阶段结构的三次捕食者-食饵扩散模型解的稳定性。文中通过建立关于时间一致的L∞(Ω)先验估计得到模型正解的整体存在性，同时应用二阶抛物型偏微分方程理论以及非线性分析方法得到模型非负平衡解的渐近稳定性。

致谢第一作者对在陕西师范大学访学期间得到导师吴建华教授悉心指点与帮助表示衷心的感谢。

[1] 曹怀火，伏升茂.一类三次捕食者-食饵扩散系统的稳定性[J].兰州大学学报：自然科学版，2008，44（4）：135-138.

[2] 贾云峰，王莹.一类带有扩散的Lotka-Volterra竞争系统的共存态[J].计算机工程与应用，2013，49（11）：35-37.

[3] Lin Z G.Time delayed parabolic system in a two-species competitive model with stage structure[J].J Math Anal Appl，2006，315：1347-1361.

[4] Xu R，Chaplain M A J，Davidson F A.Modelling and analysis of a competitive model with stage structure[J].Mathematical and Computer Modeling，2005，41：159-175.

[5] Al-Omari J F M，Courley S A.Stability and travelling fronts in Lotka-Volterra competitive models with stage structure[J].SIAM Appl Math，2003，63：2063-2086.

[6] Zhang X，Chen L S，Neamann A U.The stage-structured predator-preymodelandoptimalharvestingpolicy[J].Math Boisci，2000，168：201-210.

[7] Shen Cong，Shen Boqian.A necessary and sufficient condition of the existence and uniqueness of the limit cycles for a class of prey-predator system with sparsing effect[J].Journal of Biomathematics，2003，18（2）：207-210.

[8] Takeuchi Y.Global stability in generalized Lotka-Volterra diffusion systems[J].J Math Anal Appl，1986，116（1）：209-221.

[9] Takeuchi Y.Diffusion effect on stability of Lotka-Volterra model[J].Bull Math Biol，1986，46（5/6）：585-601.

[10] Henry D.Geometric theory of semilinear parabolic equations[M].Berlin：Springer-Verlag，1993.

[11] Cao H，Fu S.Global existence and convergence of solutions to a cross-diffusion cubic predator-prey system with stage structure for the prey[J].Boundary Value Problems，2010，2010.

[12] Fu Shengmao，Zhang Lina，Hu Ping.Global behavior of solutions in a Lotka-Volterra predator-prey model with prey-stage structure[J].Nonlinear Analysis：RWA，2013，14（5）：2027-2045.

[13] 王明新.非线性抛物型方程[M].北京：科学出版社，1993.

[14] Brown K J，Dume P C，Gardner R A.A similinear parabolic system arising in the theory of superconductivity[J].Journal of Differential Equations，1981，40：232-252.