IFOC感应电动机分岔混沌的单双时滞反馈控制

王东东， 陆益民， 张波

(1.华南理工大学电力学院，广东广州510641;2.广西大学电气工程学院，广西南宁530004)

0 引言

基于间接磁场定向控制(indirect field－oriented control，IFOC)的感应电动机系统由于动态性能优越而在实际中广为应用，然而因转子电气时间常数估计误差的存在，使系统容易产生不规则振荡现象，严重影响了IFOC感应电动机系统的运行性能。文献［1－2］研究了IFOC感应电动机系统的Hopf分岔及其在不同PI调节器参数情况下的分岔特性，从定量分析的角度对感应电动机的Hopf分岔条件进行了理论推导，获得Hopf分岔的解析表达式。文献［3－4］通过对感应电动机系统进行动力学分析，得到了系统产生混沌振荡的参数范围。

自1990年混沌控制的思想提出以来，混沌控制的研究逐渐成为热门的研究领域，其中时滞反馈控制简单可操作，只需加入适当的延迟即可实现混沌振荡的有效控制。Michiels等人分析了时滞反馈系统的稳定性，并利用时滞反馈对Lorenz系统进行混沌控制［5］。文献［6］中，利用单时滞反馈对IFOC感应电动机系统进行Hopf分岔振荡的抑制［6］。文献［7］中对几种变时滞反馈控制进行稳定性分析，推导出稳定性条件［7］。文献［8］中研究了IFOC感应电动机中的混沌现象，采用0－1混沌判别法对混沌区域进行量化［8］。文献［9］中研究讨论了IFOC感应电动机系统的混沌同步控制［9］。文献［10］中利用庞加莱截面等技术分析了IFOC感应电动机系统中的混沌现象并进行了实验验证，证实在实际的感应电机系统中混沌振荡的存在性［10］。在IFOC感应电动机系统中，由于转子电气时间常数估计不准确从而导致系统在轻载或空载时原有PI控制器失效，使系统失去稳定性而产生混沌现象。本文首先对IFOC感应电动机系统进行分岔分析，由分岔图获取其动力学特性从而得知，系统可以经由倍周期分岔进入混沌态，并产生不规则振荡。为抑制这种振荡，通过在IFOC感应电动机系统中加入时滞控制项从而实现对感应电动机系统的混沌抑制，使系统能够稳定运行，同时分析了延迟控制作用下系统的分岔行为，从分岔图和最大李雅普努夫指数中给出合适的控制器参数的选择范围。

1 IFOC感应电动机分岔混沌行为

假定感应电动机系统由电流逆变器供电，控制量为电流，则系统在同步旋转坐标系上的状态方程为［1－2］

其中:δ=npLm/Lr;ψrd，ψrq和 ωr分别为转子d、q 轴磁链和电气角速度;isd、isq为定子d、q轴电流;Tr=Lr/Rr为转子电气时间常数;Lr为转子自感;Rr为转子电阻;np为极对数;ωe=－ωr转子转速与给定值的误差。上标“*”表示相应变量的给定值。Lm为定转子互感;TL为负载转矩;J为电机转子和联接负载的转动惯量;D为粘滞摩擦系数。根据文献［3－4，10］可知在IFOC感应电动机系统中的粘滞摩擦系数数值通常较小，为单独研究转子电气时间常数对感应电动机系统稳定新的影响，文中粘滞摩擦系数均取为0。

系统(1)的平衡点为［2］

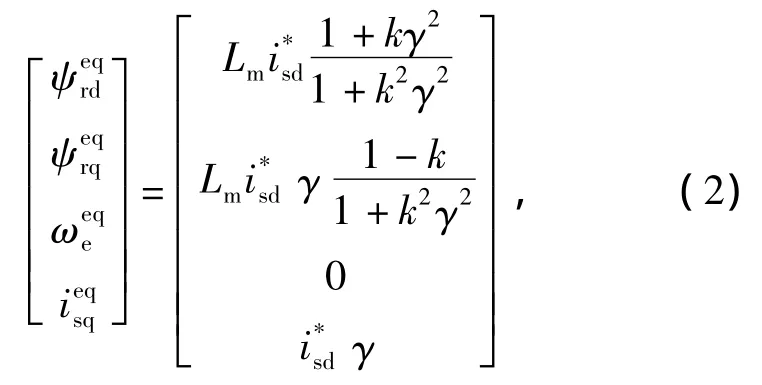
其中，γ由方程(3)确定，即

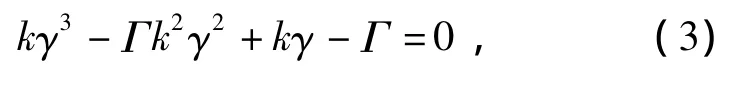
其中

电磁转矩Te=TL+D/np。由式(2)可以看出系统平衡点第三个分量为0。根据文献［3－4］，感应电动机系统参数取为:Lm=69 mH;Lr=71 mH;J==np/Tr。系统分岔图如图1所示，从图1(a)中可以看出当取负载TL为分岔参数时，随着负载TL数值的不断增加，转子直轴磁场由周期1→周期2，…，混沌，即历经倍周期分岔进入混沌态，并经历若干个周期窗口，最后由倒分岔退出混沌并进入稳态，从分岔图中可以较为清晰地观察到IFOC感应电动机系统的周期数，即转子直轴磁场时间响应的周期数目。当np=1，负载TL取不同数值时，感应电动机系统在相图上的周期数表现为1，2，4，如图2所示。图3为感应电动机系统的典型混沌吸引子。图4为np=1，2时的最大李雅普诺夫指数图，它与分岔图中的混沌区域相对应。

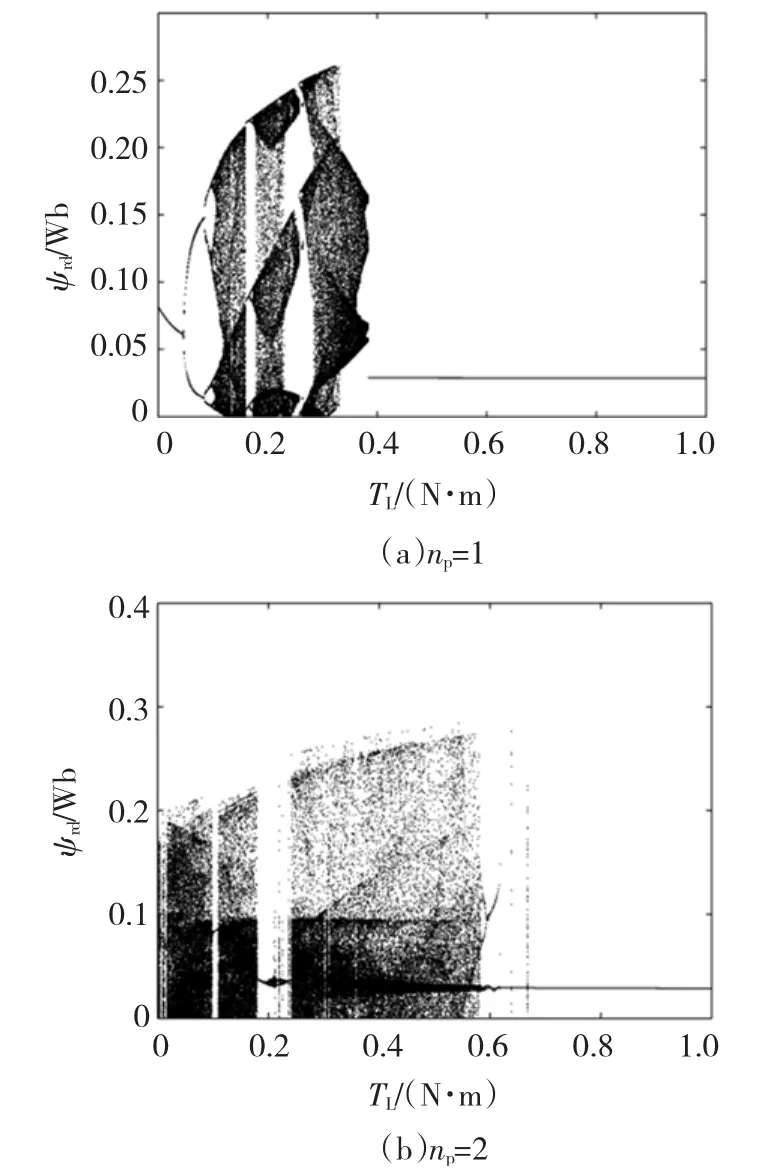
图1 ψrd的分岔图Fig.1 Bifurcation diagram of ψrd

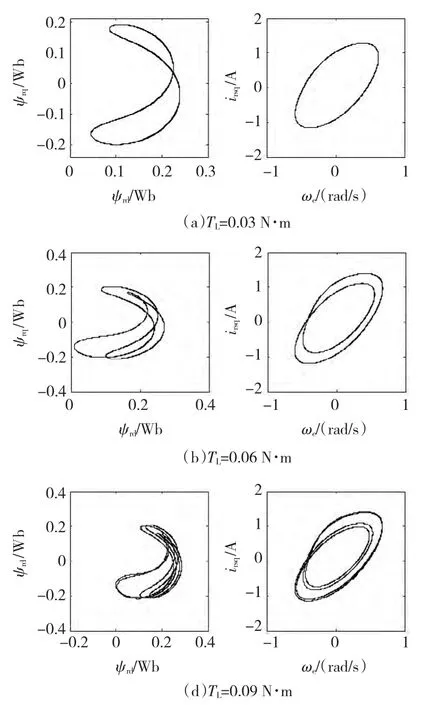
图2 np=1时的相轨迹Fig.2 Phase trajectories for np=1

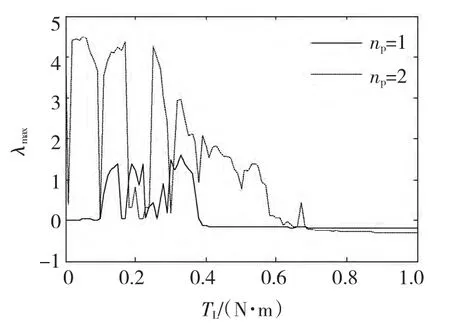
图4 最大李雅普诺夫指数Fig.4 Largest Lyapunov exponent

2 分岔混沌的时滞反馈抑制

假定有一非线性混沌系统

将系统(5)在平衡点x*=(x1，x2，…，xn)处进行线性化，则系统变为

在其中加入时滞控制项

那么，系统变为

其中，τ(t)=τ0+εf(Ωt)，f:R →［－1，1］是一个周期2π 的函数，ε ＜ τ0，取一可积函数 w:［－1，1］→ R+由下式定义

对于每一个连续函数都有α:［－1，1］→ R。

如果有系统

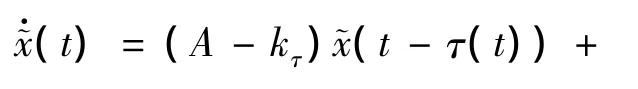
是渐进稳定的，那么，系统(7)是全局一致渐进稳定的。它的特征方程为

其中，

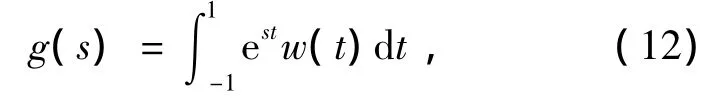
假定系统(8)的最右特征值是简单的且在虚轴上，且记为 jωi，i=1，m。如果

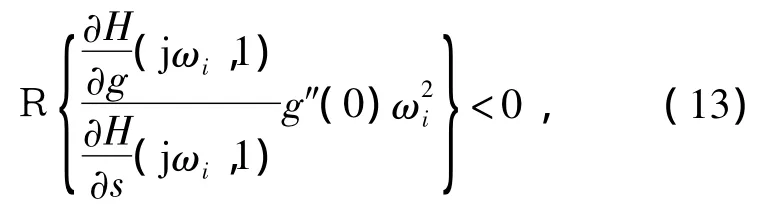
那么，当ε值较小时，系统(8)是渐进稳定的［4］。文中，将延迟时间取为常数，即取ε=0。

当IFOC感应电动机系统产生混沌振荡时，将时滞反馈项式(7)(单时滞)加入系统(1)状态方程的第四项，则得时滞状态方程为

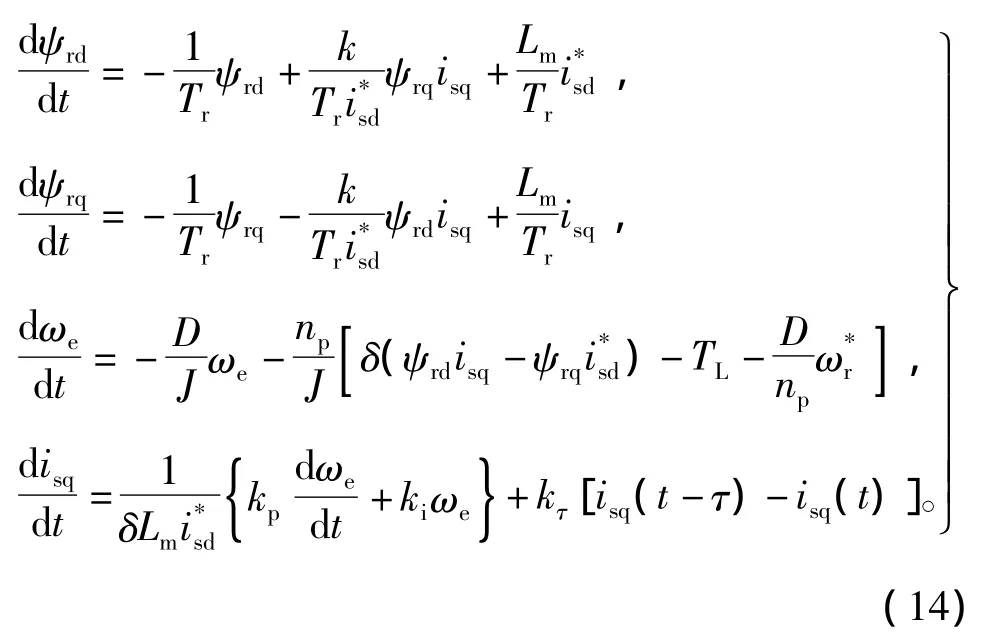
当kτ=10，TL=0.35 N·m时，感应电动机系统随τ变化的分岔图如图5所示。

在系统进入混沌态第10 s加入时滞控制项，系统时间响应如图6，控制器参数可由分岔图稳态区域中选取。由图6可见混沌现象消失，暂态时间如表1所示。

表1 暂态性能Table 1 Transient performance

对于双时滞情形，即将时滞反馈项加入状态方程第三、第四项，可得

图5 单时滞反馈系统分岔图Fig.5 Bifurcation diagram of the single time-delayed feedback

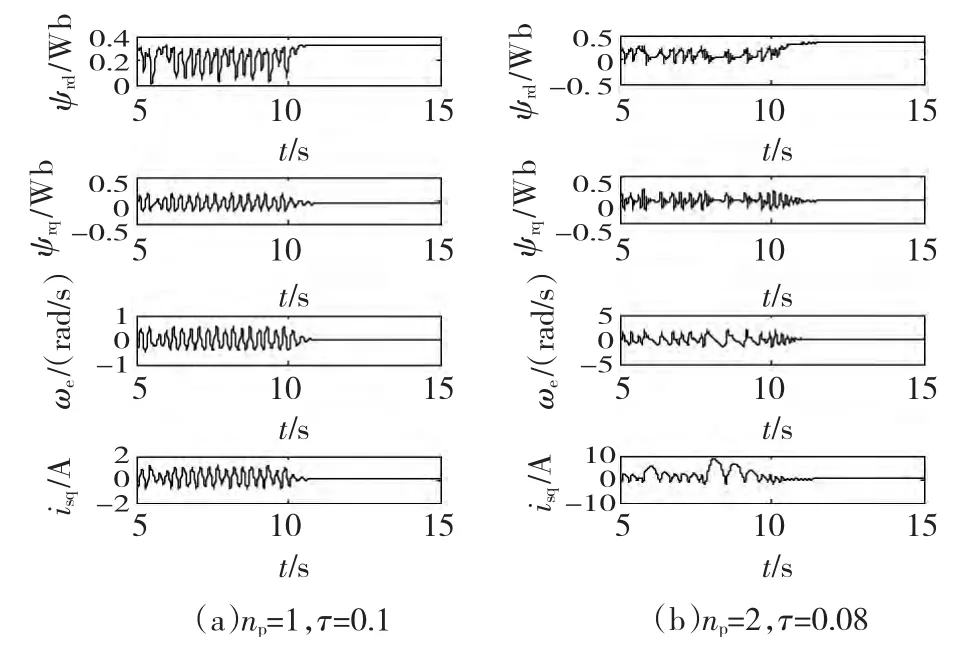
图6 单时滞反馈时间响应Fig.6 Time response of the single time-delayed feedback

为研究延迟反馈作用下反馈参数改变时IFOC感应电动机系统的动力学特性。当kτ=10，TL=0.35 N·m时，绘制感应电动机系统随延迟时间τ变化的分岔图如图7所示，从图中可以看出延迟控制项的增加使分岔图中稳态区域对应的范围略大，反应了延迟控制项数目对延迟反馈控制作用的变化趋势，即双时滞控制使系统更易稳定。

图7 双时滞反馈系统分岔图Fig.7 Bifurcation diagram of the double time-delayed feedback

在系统进入混沌态第10 s加入时滞控制项，系统时间响应如图8，暂态时间如表1所示，混沌振荡随控制项的引入而消失，系统进入平衡状态。由单时滞和双时滞的分岔图及时间响应图可以看出，双时滞稳定参数范围略大，且过渡过程变短，具有更快的响应速度。

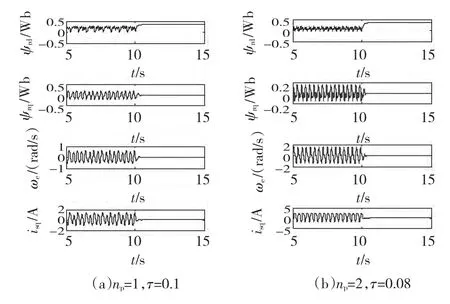
图8 双时滞反馈时间响应Fig.8 Time response of the double time-delayed feedback

4 结论

间接磁场定向感应电动机在转子电气时间常数的估计值出现误差时，将可能引起闭环系统失去稳定性，导致原有PI控制器失效，从而产生不规则振荡现象，利用分岔图该系统进行分岔分析，可知系统在不同负载参数下可由倍周期分岔的途径进入混沌态，使得感应电动机系统失去稳定性进而产生振荡现象。因此，本文利用简单的时滞反馈控制对这种混沌振荡进行抑制，采用分岔图分析延迟反馈控制项对感应电动机系统的影响，表明不同极对数情况下，延迟时间增大时系统的动力学现象，并从中选取合适的控制参数以抑制混沌振荡的出现，数值仿真结果证明这种方法是有效的。同时，文中对单时滞和双时滞的控制效果进行量化对比，可知单时滞反馈即可使系统由混沌振荡进入稳态，极对数取不同数值时IFOC感应电动机系统仍然能够进入稳态，若加入更强的双时滞反馈控制项将使得系统的暂态时间变短，控制性能更加优越，从而为实际应用中感应电动机系统不规则振荡的抑制提供理论基础。

［1］BAZANELLA A S，REGINATTO R.Robust tuning of the speed loop in indirect field oriented control of induction motors［J］.Automatica，2001，37(11):1811 －1818.

［2］GORDILLO F，SALAS F，ORTEGA R，ARACIL J.Hopf bifurcation in indirect field-oriented control of induction motors［J］，Automatica，2002，38(7):829 －835.

［3］陆益民，毛宗源，张波.感应电动机间接磁场定向控制系统振荡的功率谱分析［J］.机械工程学报.2004，40(12):5－9.LU Yimin，MAO Zongyuan，ZHANG Bo.Analysis oscillations in field oriented control of induction motor via power spectra［J］.Chinese Journal of Mechanical Engineering.2004，40(12):5－9.

［4］ZHANG Bo，LU Yimin，MAO Zongyuan.Bifurcations and chaos in indirect field-oriented control of induction motors［J］.Control Theory＆ Applications，2004，2(4)［J］:353－357.

［5］MICHIELS W，ASSCHE V V，NICULESCU S I.Stabilization of time-delay systems with a controlled time－varying delay and applications［J］.Automatic Control，2005，50(4):493 － 504.

［6］LU Yongyao，LI Hongmei and LI Wensheng，Hopf bifurcation and its control in an induction motor system with indirect field oriented control［C］//2009 Fourth Annual IEEE Industrial Electronics and Applications，May 25 －27，2009，Xi’an，China.2009:3438 －3441.

［7］GJURCHINOVSKI A，URUMOV V，Variable-delay feedback control of unstable steady states in retarded time-delayed systems［J］，Physical Review E.2010，81(1):016209 1 －12.

［8］WANG Dongdong，LU Yimin，HUANG Xianfeng.Chaos identification and suppression in an indirect field-oriented control of induction motor drive based on 0 －1 method［C］//2013 First Annual Applied Mechanics，Mechatronics and Intelligent System，Advanced Materials Research，April 19 － 21，Changsha，China，Switzerland:Trans Tech Publications，2013:194 －198.

［9］WANG Dongdong，LU Yimin.Chaos synchronization control of an indirect field-oriented induction motor［C］//2013 Second Annual International Conference on Energy and Environmental Protection，Advanced Materials Research，April 20 － 21，Guilin，China，Switzerland:Trans Tech Publications，2013:1097－1011.

［10］Zou G T，Wang Z，Cheng M.Chaotic Drives and Their Applications［M］，Beijing:Science Press，2009，chap.3.