新型双Buck并网逆变器及其双二阶滑模控制

侯世英， 邹学伟， 孙韬， 唐荣波

(1重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044;2.重庆水利电力职业技术学院，重庆402160)

0 引言

随着化石能源的日益枯竭与环境污染的不断加剧，风能、太阳能等可再生能源以其无污染、可再生、清洁安全等特性而越来越受到人们的广泛关注。而利用可再生能源发出的电能［1－2］，如风力发电的波动较大、太阳能电池输出为直流等原因都不能直接并入电网，因此在分布式发电系统中起电能变换作用的逆变器成为了不可或缺的一部分。

近年来，双Buck逆变器由于具有无功率管直通、可靠性高等优点［3－6］而成为一个研究热点。文献［5］利用三电平开关取代功率二极管的方法提出了一种三电平双Buck逆变器，降低了输出谐波含量，但没有解决电压利用率低的问题，且器件的增加造成了电路的复杂以及控制的困难。文献［4］和文献［6］则提出一种双降压全桥逆变器，提高了直流输入的利用率，减小了开关损耗，但对于滤波器的磁件体积及重量大的问题没有得到解决。基于以上两个问题，本文在原有拓扑结构的基础上提出了一种改进，不仅克服了传统拓扑直流输入利用率低的缺陷，且减少了两个滤波电感元件，大大减少了磁件的体积和重量。

在控制策略方面，针对双Buck逆变器已有大量研究文献［7－11］，这些研究大多采用经典控制理论，虽可较好地实现逆变器的功能，但对于输入扰动、输出电压电流的动态和稳态性能等方面表现出明显的不足。滑模控制是一种具有良好鲁棒性和强适用性的非线性控制方法［12－16］。将滑模控制首先应用于双Buck逆变器见于文献［14］，文章在2阶滑模控制的基础上引入了积分环节，减少了输出稳态误差;文献［15］则在文献［14］之上通过增加滤波电感电流误差构成的滑模控制器，在输出稳态误差和动态性能方面得到了较好地改善。通常新能源发电并网过程中，由于动态波动比较大，容易给电能质量造成一定的影响;且新能源发电系统大部分采用电力电子装置实现并网，而电力电子装置产生的电压谐波也是不可避免的，所以为了使改进的并网逆变器输出高质量的并网电压和电流并获得良好的动态和稳态性能，本文研究了新型拓扑的滑模控制策略，提出一种选取电压和电流双二阶状态变量的滑模控制，得到了较好的效果，仿真与实验也验证新型拓扑及控制策略的可行性和正确性。

1 新型双Buck全桥并网逆变器及工作原理

图1所示即为所提出的新型双Buck全桥并网逆变器的主电路图。其中L1、L2为滤波电感，C为滤波电容，R为并网负载，uo为输出并网电压，us为电网电压。

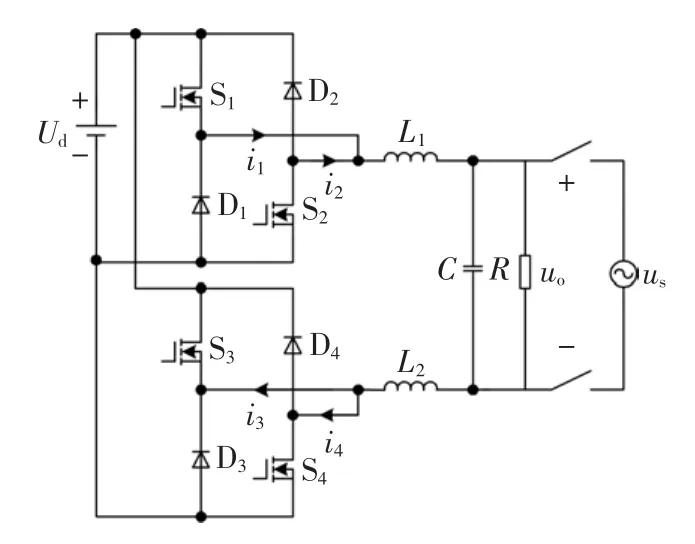
图1 双Buck全桥并网逆变器Fig.1 Dual Buck full-bridge grid-connected inverter

图2为双Buck全桥并网逆变器的主要波形示意。其中，Ugs1～Ugs4分别为开关管S1～S4的驱动信号，i1～i4为逆变器各支路电流。在电网电压正半周时，S1、S4有驱动信号，共同进行调制工作;在电网电压负半周时，S2、S3有驱动信号，共同进行调制工作。

图2 双Buck全桥并网逆变器主要波形图Fig.2 Main waveforms of the Dual Buck full-bridge grid-connected inverter

稳态时逆变器在一个工频周期内有4个工作模态，其等效电路如图3所示。

当 us＞0 时，S2、S3和 D2、D3始终关断，开关模态1和2不断重复，输出电压为uo1:

(1)开关模态 1:S1、S4导通，D1、D4关断，io=i1=i4，i1正向线性增加，如图3(a)所示。

(2)开关模态 2:S1、S4关断，D1、D4导通，io=i1=i4，i1正向线性减少，如图3(b)所示。

当 us＜0 时，S1、S4和 D1、D4始终关断，开关模态3和4不断重复，输出电压为uo2:

(3)开关模态 3:S2、S3导通，D2、D3关断，io=i2=i3，i2负向线性增加，如图3(c)所示。

(4)开关模态 4:S2、S3关断，D2、D3导通，io=i2=i3，i2负向线性减少，如图3(d)所示。

图3 各工作模态等效电路Fig.3 Equivalent circuits of each operation mode

因 L1、L2串联工作且 L1=L2，即 iL1与 iL2是完全相同的，故可在us＞0时以iL1进行分析。当电感电流连续时，设开关管的周期为Ts，开关占空比为D，则导通时间为TsD，导通期间电感电流变化量为ion，关断时间为Ts(1－D)，关断期间电感电流变化量为ioff。如图4 所示，当 S1、S4导通时，有

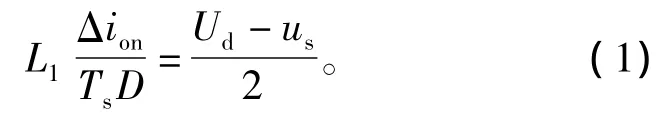
当 S1、S4关断，D1、D4导通时，有

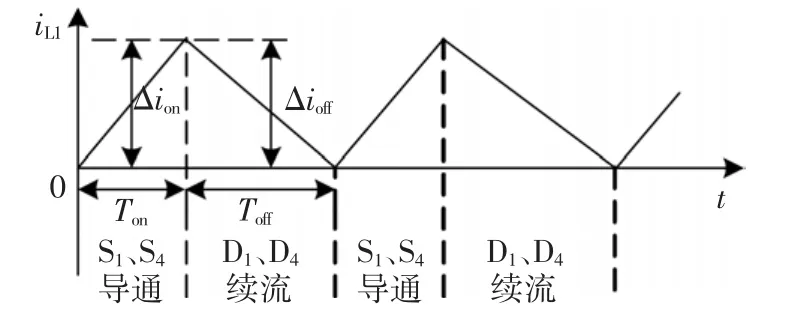
图4 在us＞0时的电感电流连续波形Fig.4 Inductor current waveform when us＞0

在一个开关周期内Δion=Δioff，由式(1)、式(2)可得输入输出电压的瞬时关系为

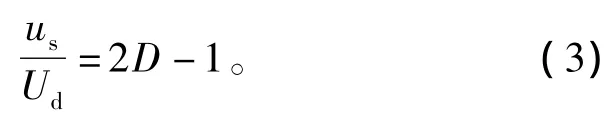
由此可知，该全桥并网逆变器的直流输入电压利用率是双Buck半桥逆变器［10］的2倍。

通过以上分析可知，双Buck全桥并网逆变器是由两组Buck变换器独立工作，可由两组滑模控制器分别控制，取us＞0时，其等效电路如图5所示，其中L=L1+L2，Uref、Iref分别是电容电压和电感电流的参考量。

选取电容电压偏差x1及其微分x2，电感电流偏差x3及其微分x4为状态变量，得到逆变器状态空间方程为

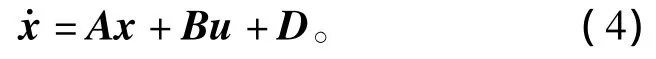
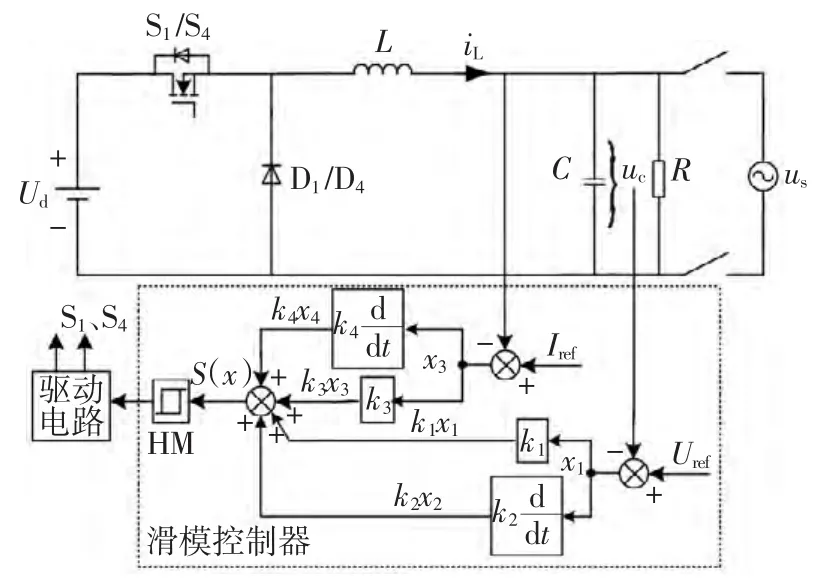
图5 双Buck并网逆变器等效电路Fig.5 Equivalent circuit of inverter system

其中

故双Buck全桥并网逆变器状态方程可定义为

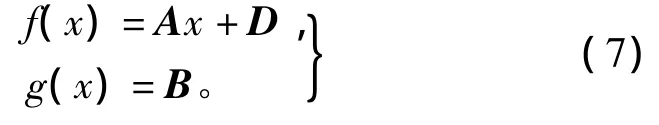
2 滑模控制器设计

在输出电容电压误差及其微分的滑模面函数的基础上，加入了电感电流误差及其微分环节，组成双二阶的滑模面控制器，如图5所示，其滑模面的选择为

其中 k1、k2、k3、k4均为正常数，可表示为

其中 KT=［k1，k2，k3，k4］为滑模面系数。滑模控制律为

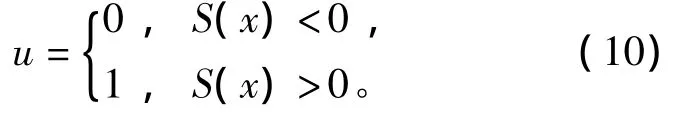
根据滑模控制理论，为了确保轨线保持于滑动线上，系统必须遵守由李亚普诺夫第二方法推导出的存在条件，它决定了系统的渐进稳定性［16］，即

于是，将式(9)对时间求导后代入上式，可得到滑模控制的存在和到达条件为

其中ξ为任意小的正数，则滑模面S(x)上存在滑模运动必要条件是

将式(4)和式(8)代入式(13)得

由式(14)知，S(x)满足存在滑模运动的必要条件。

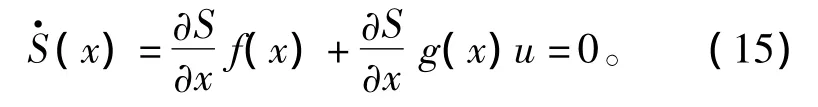
故可得到等效控制ueq为

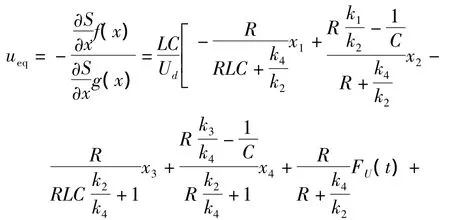
对于双Buck全桥逆变器，滑模面上存在滑模运动的充要条件是:0＜ueq＜1。

滑模面函数S(x)中，k1和k2、k3和k4分别代表系统电压、电流的稳态和动态调节特性，因此k1/k2、k3/k4的取值影响系统的动态性能;k2/k4或者k4/k2则代表滑模面函数在电压或电流动态调节性能上的倾向。就所提的双Buck逆变器来说，取k1=k3=1，k2=k4=RC可使系统在稳态和动态性能以及电压电流调节特性上都比较合理。当系统处于稳态时，Uref≈uc，Iref≈iL，因此可化简式(16)得

由于实际电路中电感L和电容C一般取值较小、R取值一般为欧姆级，且双Buck变换器中uc＜Ud，所以由式(17)可知:0＜ueq＜1，满足滑模切换面的存在和达到条件。

3 仿真分析

为了验证上述双Buck逆变器以及双二阶滑模控制策略的正确性和可行性，在Matlab/Simulink中搭建了电路模型进行仿真分析。电路仿真参数设置如下:直流输入电压 Ud=400 V，电感 L1=L2=2 mH，电容 C=470 μF，电阻 R=30 Ω，电网电压有效值为220 V，电网电压频率为50 Hz;电容电压参考信号为电网电压，电感电流参考信号与电网电压同频同相，幅值为10 A。

仿真结果如图6～图10所示。从图6可看出输出并网电压与电网电压同频同相，且幅值也相同，达到了单位功率因数并网的要求。图7是输出并网电压的频谱图，输出电压的THD=0.55%，总谐波畸变率小，输出并网电压的质量高。图8为支路电流i1、i2的波形，图9为开关管S1(S4)、S2(S3)的驱动信号，从图8和图9中可以看出逆变器工作于半周模式，与前文分析逆变器的工作模式一致，开关管的最高平率达到100 kHz。以上结果表明在双二阶滑模控制策略的新型双Buck逆变器能够很好的工作，实现其功能。

当直流输入电压扰动时，如图10所示，输入电压在15 ms时从400 V跌变到350 V，在35 ms时从350 V跃变到400 V。图10(a)、10(b)分别是传统滞环电流控制和所提双二阶滑模控制的系统输出波形图。从图中可以看出两种控制方法对输入扰动都具有很强的抑制能力，但双二阶滑模控制系统的输出电压谐波含量低，输入电压变化时输出基本不受影响。

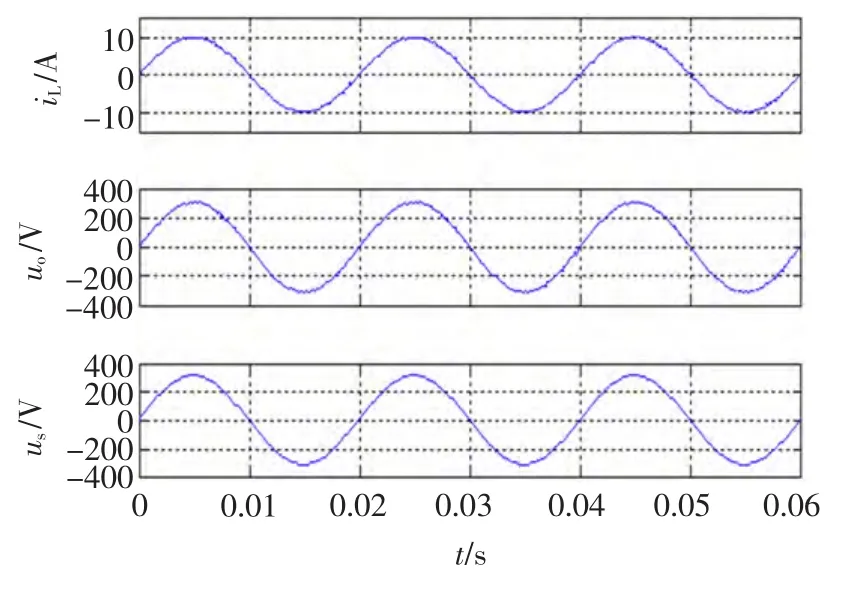
图6 电感电流、输出电压与电网电压波形Fig.6 Waveforms of inductive current，output voltage and grid voltage

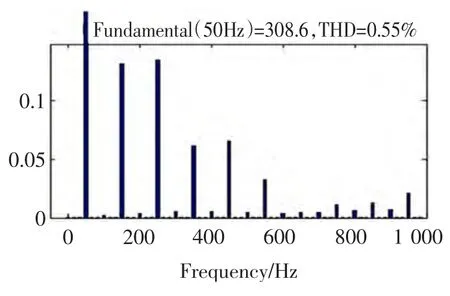
图7 输出并网电压频谱图Fig.7 Spectrum of output paralleling voltage

图8 支路电流i1与i2的波形Fig.8 Waveforms of the branch currents:i1and i2

图9 开关管S1(S4)、S2(S3)的驱动信号Fig.9 Drive signals of the switches:S1(S4)and S2(S3)

图10 输入电压扰动时输出电压和电感电流波形Fig.10 Waveforms of output voltage and inductive current during input voltage fluctuation

图11 电网电压扰动时输出电压和电感电流波形Fig.11 Waveform of output voltage and inductive current during grid voltage fluctuation

当电网电压扰动时，取电网电压波动为15%，如图11所示，电网电压的有效值在15 ms时从220 V跃变到253 V，在35 ms时从253 V跌变到220 V。图11(a)、11(b)分别是传统滞环电流控制和所提双二阶滑模控制的系统输出波形图。从图中可以看出传统滞环电流控制下系统输出电压和电感电流有一定的畸变，其原因是电压反馈的参考量来自于电网侧电压，在突然改变电网电压时，滞环比较的输入有一定的改变，导致输出产生了变化。而相较于滞环电流控制，双二阶滑模控制在电网侧电压变化时动态响应很快，输出基本不受影响，具有很强的鲁棒性和动态性能。

4 实验验证

为了进一步验证上述理论和仿真分析，设计了一台最大输出功率为100W的原理样机，其电路参数与仿真一致，输入为100V(由 Circuit Specilists 12005S直流电源提供)，后级输出经60 V/220 V工频变压器接入电网，得到如下部分实验波形图。

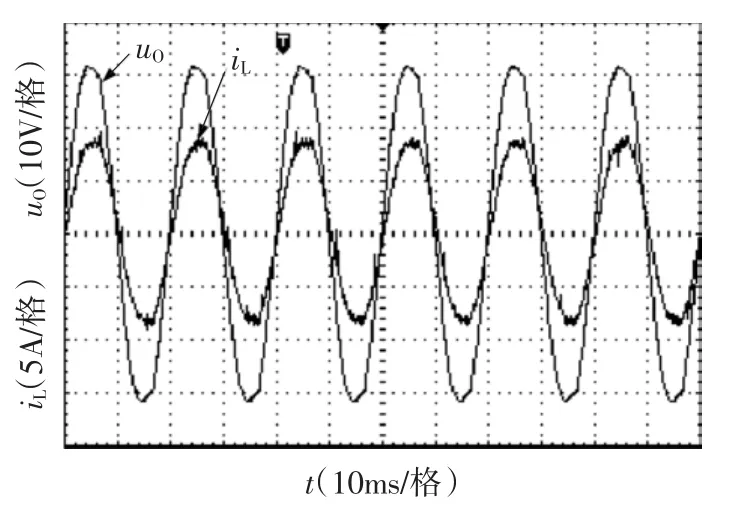
图12 满载时系统输出电压和电感电流波形Fig.12 Steady state output voltage and inductive current under double-loop sliding mode control

图13 支路电流i1与i2的波形Fig.13 Waveforms of the branch currents:i1and i2

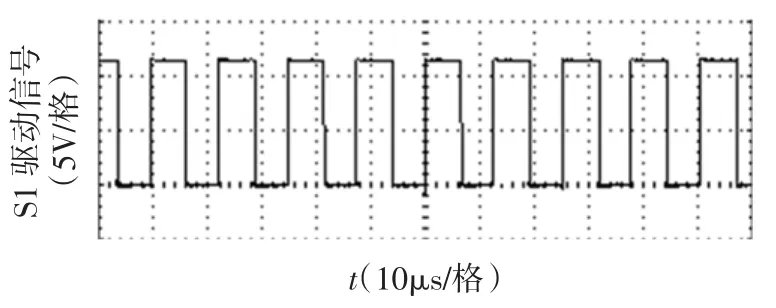
图14 稳态时开关管S1的驱动信号Fig.14 Drive signals of the switch S1

图15 负载突变时输出电压和输出电流波形Fig.15 Output voltage and current transient responses with a sudden load change

图11为双二阶滑模控制下满载时(R为30 Ω/200 W)双Buck逆变器输出电压和电感电流波形;图12为支路电流i1、i2的波形，图13为开关管S1的驱动信号，稳态时开关频率最高为80 kHz，实验结果为与仿真基本一致，验证了本文所采用的控制策略下新型双Buck逆变器系统的正确性。

图14为负载突变实验波形，其中图14(a)是从空载突然到满载的输出电压和输出电流波形，图14(b)是从空载突然到满载的输出电压和输出电流波形，结果表明所采用的双二阶滑模控制策略具有较强的鲁棒性和动态性能。

5 结论

本文提出了一种改进的双Buck全桥并网逆变器，克服了传统拓扑直流输入利用率和磁件体积重量的问题，在分析其工作原理后，选取以电容电压偏差x1及其微分x2、电感电流偏差x3及其微分x4为状态变量，推导出其状态空间表达式，然后给出了其滑模控制器的设计。最后进行了仿真与实验分析，结果表明在双二阶滑模控制策略下的新型双Buck逆变器具有较好的动态和稳态性能，且对直流输入和电网电压扰动有较强的抑制作用。事实上，并网技术的发展直接影响着新能源发电的发展和使用，故本文所提拓扑和控制方法比较适应于新能源发电的并网，具有一定的实用价值。

［1］SKEA J，ANDERSON D，GREEN T，et al.Intermittent renewable generation and maintaining power system reliability［J］.Generation，Transmission ＆ Distribution，IET，2008，2(1):82－89.

［2］Juan Manuel Carrasco，Leopoldo Garcia Franquelo，Jan T.Bialasiewicz.Power-electronic systems for the grid integration of renewable energy sources:a survey［J］.IEEE Transactions on Industrial Electronics，2006，53(4):1002－1016.

［3］SUN Pengwei，LIU Chuang，et al.Three － phase dual－ buck inverter with unified pulsewidth modulation［J］.IEEE Transactions on Power Electronics，2012，27(3):1159 －1167.

［4］吴婷，肖岚，姚志垒.双降压式全桥逆变器［J］.中国电机工程学报，2009，29(15):22 －27.WU Ting，XIAO Lan，YAO Zhilei.Dual buck full－ bridge inverter［J］.Proceedings of the CSEE，2009，29(15):22 －27.

［5］嵇保健，赵剑锋，洪峰.一种新颖的三电平双 Buck逆变器［J］.电工技术学报，2011，26:148－153.JI Baojian，ZHAO Jianfeng，HONG Feng.A novel three level dual Buck inverter［J］.Transaction of China Electrotechnical Society，2011，26:148－153.

［6］姚志垒，肖岚，魏星.双降压全桥并网逆变器［J］.中国电机工程学报，2011，31(12):29 －33.YAO Zhilei，XIAO Lan，WEI xing.Dual buck full-bridge gridconnected inverter［J］.Proceedings of the CSEE，2011，31(12):29－33.

［7］马海啸，严仰光.半桥双降压式逆变器的电压谐振控制策略［J］.电力自动化设备，2012，32(7):66 －70.MA Haixiao，YAN Yangguang.A voltage harmonic control strategy for half bridge dual Buck inverter［J］.Electric Power Automation Equipment，2012，32(7):66 －70.

［8］YAO Zhilei.Two-switch dual-buck grid-connected inverter［J］.IEEE 6th International Power Electronics and Motion Control Conference，IPEMC ＇09 Wuhan，China.2009:2182 －2187.

［9］LIU Jun，WANG Huizhen，YAN Yangguang.A novel three level dual buck half bridge inverter［J］.IEEE Twenty-Third Annual Applied Power Electronics Conference and Exposition，2008.APEC 2008:483－487.

［10］洪峰，刘军.滞环电流控制型双BUCK逆变器［J］.电工技术学报，2004，19(8):73 －77.HONG Feng，LIU Jun.Hysteresis current control for dual Buck inverter［J］.Transaction of China Electrotechnical Society，2004，19(8):73 －77.

［11］周雒维，彭容，杜雄.单周控制双Buck型电压源换流器［J］.中国电机工程学报，2005，25(17):11 －14.ZHOU Luowei，PENG Rong，DU Xiong.Single cycle control double buck voltage source inverter［J］.Proceedings of the CSEE，2005，25(17):11 －14.

［12］Rojas-Gonzalez，M.A.An integrated dual-output buck converter based on sliding mode control［J］.IEEE Third Latin American Symposium on Circuits and Systems(LASCAS)，2012:1－4.

［13］GONG Cheng，WAN Jianru，LI Kunpeng，et al.Direct capacitor power control of dual PWM converter based on sliding mode variable structure［J］.IEEE Innovative Smart Grid Technologies-Asia(ISGT Asia)，2012:1－5.

［14］许飞，马皓，何湘宁.新型Buck逆变器3阶滑模控制策略［J］.中国电机工程学报，2009，29(12):41 －46.XU Fei，MA Hao，HE Xiangning.Novel three-order sliding mode control strategy for buck inverter［J］.Proceedings of the CSEE，2009，29(12):41 －46.

［15］陈江辉，谢运祥，谢涛，等.双Buck型逆变器高阶系统二阶滑模控制［J］.电机与控制学报，2010，14(11):76－81.CHEN Jianghui，XIE Yunxiang，XIE Tao，et al.Second-order sliding mode control based on dual Buck inverters［J］.Electric Machines and Control，2010，14(11):76 －81.

［16］王晓刚，张杰.电力电子变换器的滑模控制技术与实现［M］.北京:电子工业出版社，2012.