Halbach阵列同心式磁力齿轮磁场全局解析法分析

井立兵， 章跃进

(1.三峡大学电气与新能源学院，湖北宜昌443002;2.新能源微电网湖北省协同创新中心，湖北宜昌443002;3.上海大学机电工程与自动化学院，上海200072)

0 引言

同心式磁力齿轮是一种新型磁力传动装置，其内、外转子为同心式结构，中间采用调磁环对内外转子形成的磁场进行调制，使其具有一定的传动比。磁力齿轮较传统齿轮具有噪声小、稳定性强、维护成本低和过载自我保护等优点。所以磁力齿轮已经越来越受到科研人员的重视［1－2］，目前国内外对磁力齿轮进行的理论与实验研究已取得了一些进展［3－4］。但这种磁力齿轮配备旋转电机更适合用在低转速大转矩的电动汽车［5］和风力发电机上［6］。

气隙磁场分析是电机设计和性能计算的基础。气隙磁场可以采用解析法或半解析法或数值法(有限元法)求解得到。有限元法计算精确度高，但计算时间长，且需要以良好的网格品质保证其高精确度。文献［7］首次提出磁场调制式磁力齿轮机械结构及运行原理，采用磁密频谱分析法研究了气隙中调制磁场的谐波数目及所对应的传动比;文献［8－9］研究了磁力齿轮的结构参数对气隙磁密及转矩特性的影响;文献［10］则基于电动机齿槽转矩原理研究了磁力齿轮如何避免齿槽转矩的产生。上述文献的共同特点是对气隙磁场及传动转矩的分析采用有限元法。而文献［11－12］则采用有限元法对装置的磁性能进行了仿真。

图1是同心式磁力齿轮结构示意，它是由内转子、外转子、内外转子永磁体及调磁环构成，调磁环是由圆周均布的导磁和非导磁材料组成。尽管有一些文献在处理开槽电机时有详细的论述［13－14］，但这种两边都开槽的调磁环在气隙磁场中是很难处理的。

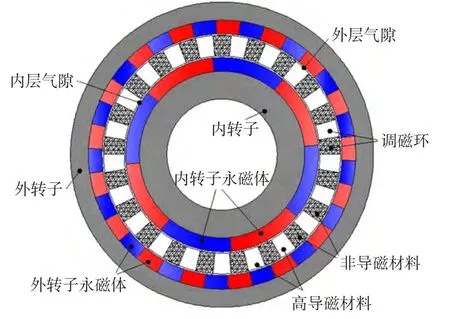
图1 磁力齿轮结构示意Fig.1 Geometryof the concentric magnetic gear

Halbach阵列充磁的永磁体气隙磁场与传统永磁电机气隙磁场相比，正弦分布程度较高，谐波含量小，且聚磁效应明显［15］。基于此在文献［16－17］的基础上，把原来径向充磁改为Halbach阵列充磁，建立Halbach充磁解析模型;应用全局解析法分析Halbach阵列同心式磁力齿轮。避免了有限元法在剖分网格和曲面位置选择上的不足，实现了内外两转子自由转动。以一种Halbach阵列同心式磁力齿轮样机为例，计算了气隙磁场和电磁转矩，并与有限元法结果比较，验证方法的正确性。

1 Halbach阵列解析模型

从图1可知，调磁环所起的作用是调制两气隙磁场，对永磁体而言，一般来说都是径向充磁，为了得到较高的磁密，需要改变永磁体的充磁方向，而Halbach阵列永磁体正好符合这个要求。

图2是一对极下内外转子永磁体平面图，其中内转子每一极下永磁体分为3小块永磁体;而外转子每一极下永磁体分为2小块永磁体。图中的箭头方向表示的是每块永磁体的充磁方向。

图2 永磁体块充磁示意Fig.2 Arrangements of PM segments

此时永磁体的磁化强度M的表达式为

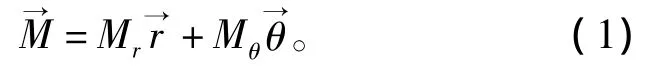
其中:

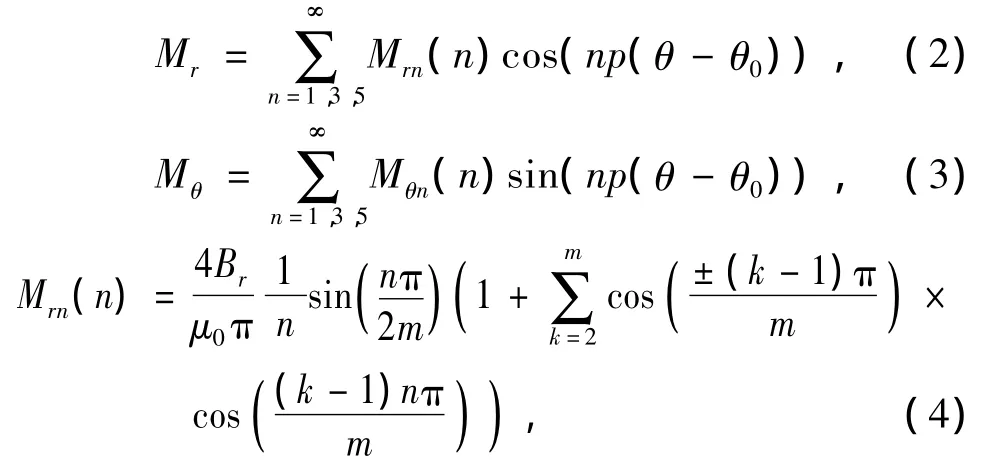
式中“+”代表外转子;“－”代表内转子;p是极对数;mg为每一极下永磁体所分块数;g为m块中的第k块;θw为永磁体中心线与基准线r轴初始位置角度;Br为永磁体剩磁;μ0为真空磁导率。

2 解析分析

1)气隙区域磁场

气隙区域磁场是有内外转子永磁体共同作用得到的，为了分析磁场的方便，下面做一些假设:

(1)忽略端部效应;

(2)铁心磁导率无穷大;

(3)永磁体相对磁导率等于1。

内外转子永磁体、内外两层气隙和调磁定子的槽形区域，3类区域的拉普拉斯方程和泊松方程通过边界连续条件建立联系，根据分离变量法可以求得解析解。即可得到各区域矢量磁位方程。分别对内气隙矢量磁位和外气隙矢量磁位求偏导，就可得到气隙磁场径向磁密和切向磁密。在此给出内外两层气隙磁场径向磁密和切向磁密解析表达式。

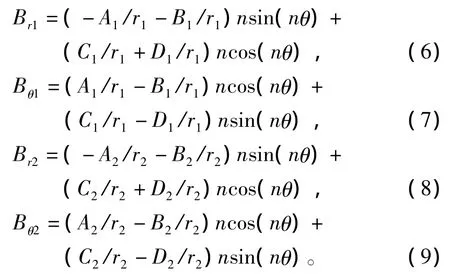
r1和r2分别是内气隙和外气隙中间值;系数A1，B1，C1，D1和 A2，B2，C2，D2是半径 r 的函数。

2)槽区域的解

图3是第i槽的结构示意，槽区域的拉普拉斯方程表示为

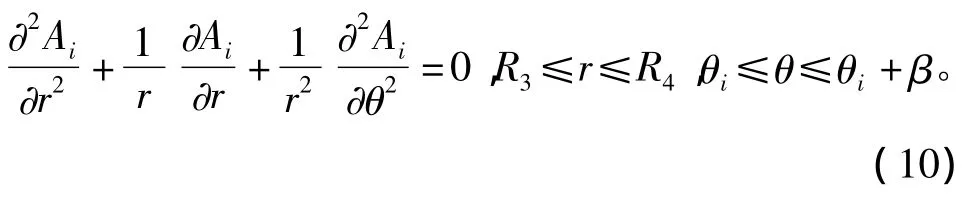
其中R3和R4分别是槽区域的内半径和外半径，β是槽的开口角度，θi是第i槽的位置角。

第i槽区域的边界条件是(槽区域磁场切向方向为0)。

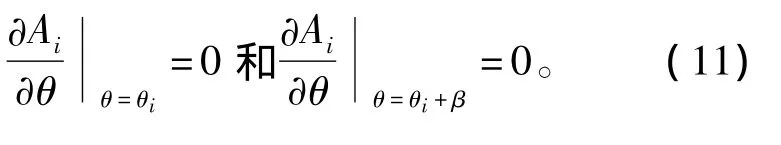
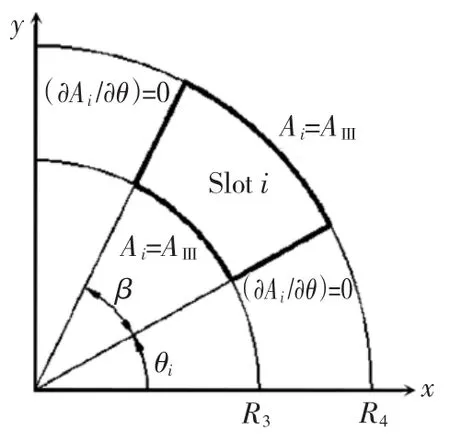
图3 第i槽区域边界条件Fig.3 ith slot subdomain with its boundary condition

根据分离变量法，由式(10)可以得到

3)电磁转矩

根据麦克斯韦应力张量法理论，电磁转矩的表达式可表示为

式中:Lef为电机气隙轴向有效长度;r为气隙中的任意圆周半径;Brn，Bθn分别为半径r处气隙磁密的径向和切向分量。对于选定的半径，r为常数。

3 计算实例

为了验证全局解析法计算的有效性，本文利用以上解析计算模型，对一台Halbach阵列同心式磁力齿轮样机内外两层气隙磁场和电磁转矩进行计算，表1给出了样机参数。

表1 磁力齿轮参数Table 1 Parameters of magnetic gear

两种充磁方式下磁力线的分布情况如图4所示。从图中可知，在内外转子轭部Halbach阵列充磁磁密较同部位径向充磁磁密小很多，因此转子材料就有所减少，降低了体积及成本。

图4 磁力线分布Fig.4 magnetic field distributions

图5为内层气隙径向磁密和切向磁密解析计算结果和有限元计算结果的比较。

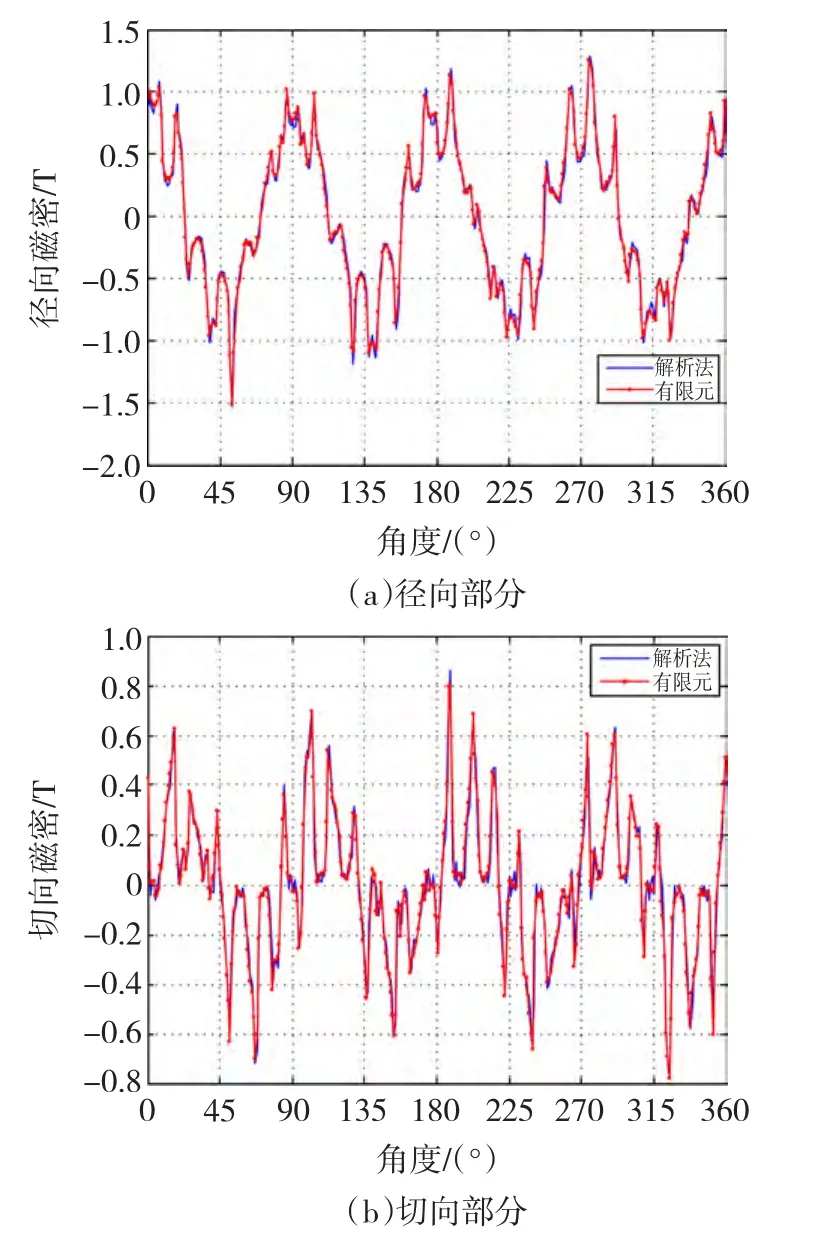
图5 内层气隙中间磁通密度Fig.5 Flux density distribution in the middle of the inner air-gap

图6为外层气隙径向磁密和切向磁密解析计算结果和有限元计算结果的比较。

图6 外层气隙中间磁通密度Fig.6 Flux density distribution in the middle of the outer air-gap

从图4和图5可知，全局解析法计算内外两层径向和切向磁密相对有限元计算结果在波形上吻合较好，这表明本解析方法是准确有效的。

利用本方法计算Halbach阵列同心式磁力齿轮的静态电磁转矩，首先固定调磁定子槽和外转子永磁体的位置，每隔4.5°转动内转子永磁体。得到的静态转矩波形如图7所示。

图7 矩角特性Fig.7 Torque-angle curves

其磁场静态转矩波形均近似为正弦波，转矩的大小随着内外转子永磁体相对位置的变化而变化，这与同步电机中的矩角特性相类似;内外转子上的转矩比值在任意位置都基本为－1:4.25，这与其传动比是一致的;且内转子永磁体在转到22.5°时得到最大静态转矩值。

图8是内、外转子在两种充磁下的电磁转矩比较图。对内转子来说，在径向充磁下最大静态转矩为29.8 N·m;而在Halbach阵列充磁下，最大静态转矩为35.0 N·m，这比径向充磁下的电磁转矩的大小提高了17.5%。对外转子来说，在径向充磁下最大静态转矩为136.55 N·m;而在Halbach阵列充磁下，最大静态转矩为148.8 N·m，这比径向充磁下的电磁转矩的大小也提高了17.5%。因此，在同体积下的磁力齿轮，其转矩密度也要提高17.5%。可见磁力齿轮在Halbach阵列充磁下具有完美的特性。

图8 矩角特性Fig.8 Torque-angle curves

4 结论

本文采用全局解析法计算Halbach阵列同心式磁力齿轮磁场分布及电磁转矩。建立了Halbach阵列充磁解析模型，通过实例模型计算了内外两层气隙磁场和电磁转矩，其计算波形与有限元法计算波形很吻合。从计算结果看，Halbach阵列充磁下同心式磁力齿轮的电磁转矩较径向充磁下电磁转矩有所提高，证明了本方法的正确性和有效性。同时为同心式磁力齿轮复合电机的设计提供了一种有效的方法。

［1］刘占生，崔亚辉，叶建槐，等.非线性油膜力和啮合力作用下齿轮系统的振动特性研究［J］.中国电机工程学报，2009，29(23):84－91.LIU Zhansheng，CUI Yahui，YE Jianhuai，et al.Research on vibration characteristics of gear system with nonlinear oil film force and mesh force［J］.Proceedings of the CSEE，2009，29(23):84 －91.

［2］张东，邹国棠，江建中，等.新型外转子磁齿轮复合电机的设计与研究［J］.中国电机工程学报，2008，28(30):67－72.ZHANG Dong，ZOU Guotang，JIANG Jianzhong，et al.Design and research of a novel magnetic-geared outer-rotor compact machine［J］.Proceedings of the CSEE，2008，28(30):67 －72.

［3］YEH Y，HSIEH M，DORRELL D G.Different arrangements for dual-rotor dual-output radial-flux motors［C］//IEEE Energy Conversion Congress and Exposition，2010:2956 －2962.

［4］FU W N，HO S L.A quantitative comparative analysis of a novel flux-modulated permanent-magnet motor for low-speed drives［J］.IEEE Transactions on Magnetics，2010，46(1):127 －134.

［5］CHAU K T，ZHANG D，JIANG J Z，et al.Design of a magneticgeared outer-rotor permanent-magnetic brushless motor for electric vehicles［J］.IEEE Transactions on Magnetics，2007，43(6):2504－2506.

［6］JIAN L，CHAU K T，JIANG J Z.A magnetic geared outer-rotor permanent-magnet brushless machine for wind power generation［J］.IEEE Transactions on Industry Applications，2009，35(3):954－992.

［7］ATALLAH K，HOWE D.A novel high performance magnetic gear［J］.IEEE Transactions on Magnetics，2001，37(4):2844－2846.

［8］ATALLAH K，HOWE D.Design，analysis and realization of a high-performance magnetic gear［J］.IEEE Proceedings Electric Power Applications，2004，151(2):135 －143.

［9］RASMUSSEN P O，ANDERSEN T O，JORGENSEN F T.Development of a high-performance magnetic gear［J］.IEEE Transactions on Industry Applications，2005，41(3):764 －770.

［10］NIGUCHI N，HIRATA K.Cogging torque analysis of magnetic gear［J］.IEEE Transactions on Industrial Electronics，2011，99(6):1－9.

［11］CAO Z T，CAI J J，CHEN H P，et al.FEM coupling field iteration and its convergence for a GMM acturator［J］.Chinese Journal of Mechanical Engineering，2005，18(1):79 －82.

［12］ZENG P，LEI L P，ZHAO R H，et al.Numerical analyses of design and assembly for main components of BESIII［J］.Chinese Journal of Mechanical Engineering，2007，20(5):96 －100.

［13］ZHU Z Q，HOWE D.Instantaneous magnetic-field distribution in brushless permanent-magnet dc motor，part III:Effect of slotting［J］.IEEE Transactions on Magnetics，1993，29(1):143－151.

［14］LIU Z J，LI J T.Accurate prediction of magnetic field and magnetic forces in permanent magnet motor using an analytical solution［J］.IEEE Transactions on Energy Conversion，2008，23(3):717－726.

［15］JIAN L，CHAU K T.A coaxial magnetic gear with Halbach permanent-magnet arrays［J］.IEEE Transactions on Energy Conversion，2010，25(2):319－328.

［16］井立兵，章跃进.同心式磁力齿轮磁场及转矩全局解析法分析［J］.中国电机工程学报，2012，32(30):139－146.JING Libing，ZHANG Yuejin.An exact analytical method for magnetic field computation and electromagnetic torque in a concentric magnetic gear［J］.Proceedings of the CSEE，2012，32(30):139－146.

［17］LUBIN T，MEZANI S，REZZOUG A.Analytical computation of the magnetic field distribution in a magnetic gear［J］.IEEE Transactions on Magnetics，2010，46(7):2611 －2621.