海底管线服役条件有限元应力分析

杨专钊，杨 溪，惠 非，王佐强，赵晗君，冯 慧

（1.北京隆盛泰科石油管科技有限公司，北京 100101；2.中国石油集团石油管工程技术研究院，西安710077；3.中海石油（中国）有限公司深圳分公司，深圳 518067）

0 前 言

随着国内外海洋油气开发战略的不断加强，海洋油气开发逐步得到发展。恶劣的深海服役条件急需开发适用于深海油气输送管道工程的焊管产品，以便与海洋油气开发、储运工作协调发展。

但是，海底环境条件非常复杂，海底管道在海底服役时，除受输送压力和外界水压作用外，还遭受海水冲刷、涌动、昼夜温差应力及海水腐蚀等作用。所以，海底管道受力分析影响因素和影响幅度难于准确定位和测量，而且现场试验条件有限，试验难度很大，因此采用有限元法模拟海底主要服役条件，模拟计算管道海底受力状态，可为海底管道工程设计和受力分析提供参考。

本研究以此为背景，采用ANSYS有限元法模拟计算了 φ559 mm×28 mm SMYS 450（相当于API SPEC 5L X65）钢管在输送压力为25 MPa。水深为1 500 m环境下的钢管壁厚内应力分布情况。

1 材料常数和参数设定及模型建立

海底管道为有限长度的柱状体，在柱状体上作用的面力和体力方向平行于管道轴向（长度方向），而且不沿管道长度方向变化而变化，所以，近似认为这种问题属于平面应变问题。

钢管材料采用低合金高强度厚壁管线钢材料，主要成分为C-Mn钢，材料为各项同性，材料屈服强度为450 MPa。管体和配重尺寸如图1所示，钢管外径为559 mm，钢管壁厚28 mm，配重厚度为100 mm，配重材料为钢丝网混凝土。这里忽略了钢管外层的PE涂覆层厚度及其涂层对钢管应力的影响。管体材料与配重材料常数见表1。

图1 钢管及其配重尺寸

表1 管体材料与配重材料常数

假设1 500 m水深下的海水密度为恒定的，实际海水密度是温度、盐度和压力的函数，所产生的海水环境压力为15 MPa。忽略了海水流动和涌动对受力的影响，以及海水腐蚀影响。海底环境因昼夜、季节变换温差引起的应力忽略不计。

根据管道结构的对称性，为减少计算工作量，取1/4截面建立模型进行计算，模型如图2所示。内层A1面为钢管管体，外层A3面为配重层，采用Glue将A1和A3进行粘接。按照上述参数设定单元类型和划分单元网格。在模型水平线和竖直线上分别施加位移约束，Uy=0和Ux=0，即模型水平线段L4和L9的y向位移为0，线段L2和L10的x向位移为0。然后在L3加载内压25 MPa，L5上加载外压15 MPa。其载荷图如图3所示。

图2 管体和配重模型

图3 施加的约束与载荷

2 计算结果讨论与分析

2.1 位移与应变的计算

变形前后的位移分布如图4所示。最大位移为0.046 4×10-3m，发生在管体上，均匀分布；配重层内应变在壁厚中心最小，在中心两侧逐渐递增，如图5所示。

2.2 x，y，z三向应力分量的计算

ST即y向应力分量，切向应力，最大约31.07 MPa。从管体内表面开始在整个钢管壁厚范围内均匀递减至26 mm时，约25.46 MPa，到钢管外表面处，骤然降低到约0.23 MPa，到配重层外侧约为-4.5 MPa。SR为x向应力分量，径向应力，从管体内表面、管体外表面，再到配重层外表面逐步递增，应力分别为-25 MPa，-19.4 MPa和-14.5 MPa。z向应力分量Sz在管体内和配重层内均是恒定的，数值分别为1.6 MPa和-2 MPa。x，y，z 3向应力分量的计算结果如图6所示。

图4 变形前后与位移示意图

图5 总应变云图

图6 3向应力分量计算结果

2.3 主应力及Von mises等效应力的计算

随着钢管内表面距离的增加，主应力σ1和σ2随壁厚增加逐渐递减，到界面附近处出现明显极值或跳动，主应力σ1峰值在管体外表面，最大约为35 MPa；而主应力σ3是随到钢管内表面距离增加而增加，在界面附近处出现极小值，为 29.89 MPa。 在管体内， σ1>σ2>σ3； 在配重层内，σ1和σ2在相当水平，均大于σ3。Von mises等效应力σe在管体内表面和配重层均为最大。3个主应力 σ1， σ2， σ3及 Von mises等效应力 σe远小于管体材料屈服强度下限450 MPa，管体是安全的，其应力分布如图7所示。

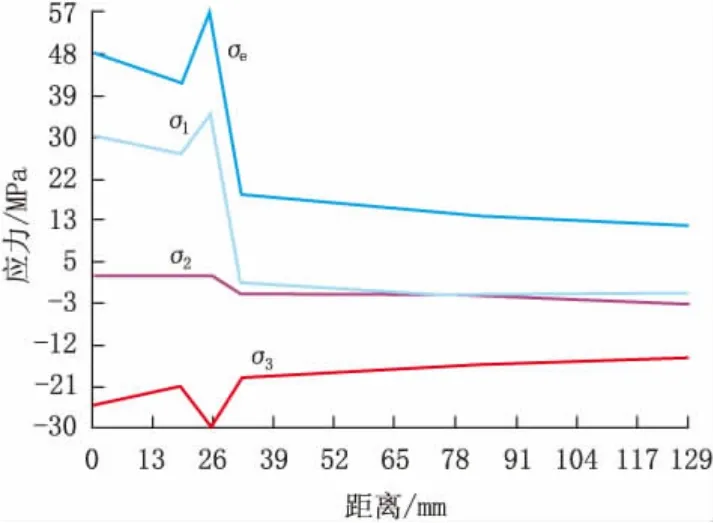
图7 主应力及Von Mises等效应力计算结果

第一主应力最大值在界面处为128 MPa，最小值在配重层的外表面处，为-1.9 MPa。Von mises等效应力分布，最大为拉应力216 MPa，在管体和配重层界面处；最小在配重层的外表处，也是拉应力，为12.3 MPa。第一主应力与Von mises等效应力分布云图如图8和图9所示。

图8 第一主应力分布云图

图9 Von mises Stress分布云图

2.4 主应变及Von mises等效应变的计算

第一主应变Strain 1st从内壁开始，随壁厚的增加平稳递减，但在26 mm附近发生微小跳动，最大为0.796×10-3。第二主应变Strain 2nd，在管体壁厚至配重层中心，恒定-0.012 5×10-3，随后开始减缓。第三主应变Strain 3rd在管体壁厚内先缓慢增加，随后迅速递减，到外表面达到最小-0.970×10-3， 随后缓慢增加到-0.71×10-3。而 Von mises应变，最小为 0.2×10-3，最大为0.001 05。主应变与Von mises等效应变路径投影如图10所示，分布云图如图11~图13所示。

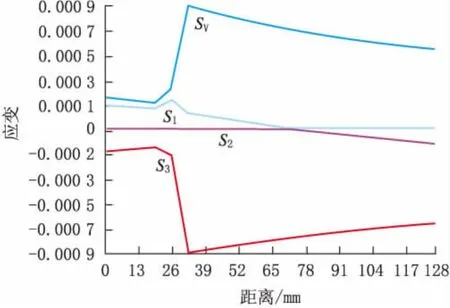
图10 主应变及Von Mises等效应变

图11 第三主应变分布云图

图12 第一主应变分布云图

图13 Von mises应变分布云图

2.5 配重层对应力应变的影响

配重层对主应力、主应变、等效应力和等效应变的影响见表2。

表2 配重层对应力与应变的影响

有配重时，自由变形受配重层约束，最大位移为0.046 4×10-3m；而无配重时，自由变形无外界约束，最大位移为0.104×10-3m，是带配重最大位移的2.5倍。由于配重层弹性模量约为管体弹性模量的1/10，当施加内压力时，配重层束缚管体发生大变形，从而限制位移。

第一主应力无配重时，最大值为80.3 MPa；有配重时，最大值为128 MPa。Von mises等效应力无配重时，最大值为91.5 MPa；有配重时，最大值为216 MPa。第一主应变无配重时最大值为0.413×10-3； 有配重时最大值为 0.796×10-3， 是无配重的2倍左右，这是由于变形受配重层约束，管体应变增加，相应应变能增加。Von mises等效应变在有配重时最大值高达1.05×10-3，是无配重层0.457×10-3的2倍多。

由于配重层弹性模量约为管体弹性模量的1/10，当施加内压力时，配重层小变形束缚管体发生大变形。因而，在有配重层的管体内比无配重层产生较大的应变和应力。

可见Von mises等效应力远高于第一主应力，Von mises等效应变也高于第一主应变。因此，对于此类管体内外约束的平面问题，采用Von mises等效应力作为验收准则是合理可行的。

3 结论与建议

综合上述模拟和计算结果，得出如下结论与建议：

（1）采用有限元法模拟海管服役条件下受力情况是可行可靠的；

（2）受配重层约束，自由变形最大位移为0.046 4×10-3m，无配重约束位移为0.104×10-3m；

（3）应力分析中，Von mises等效应力是最大的，符合Von mises准则，可以此来判断海底管道结构的安全性；

（4）第一主应力和Von mises等效应力的最大值均分布在管体材料和配重层之间的界面处附近，距离管体外表面约2 mm（壁厚28 mm），因此，管体材料表面应该光滑过渡，不应该有超过2 mm的表面缺欠或缺陷；

（5）不论是第一主应力还是Von mises等效应力，由于界面处应力最大，最小近100 MPa，这就需要考虑管体和配重之间的防腐层3PE的材料抗压性能，3PE的压缩强度一般为4~20 MPa；

（6）本研究未考虑海水流动、涌动、海水腐蚀、季节或者昼夜温差等因素对服役海管应力分布的影响，因而后续应该开展此方面的研究工作。

［1］DNV OS F101， Submarine Pipeline Systems［S］.

［2］API SPEC 5L， Specification For Line Pipe［S］.

［3］YANG Z Z， LIU D X， ZHANG X H.Finite Element Methods Analysis of the Stress for Line Pipe with Corrode Groove During Outdoor Storage［J］.Acta Metall.Sin.（Engl.Lett.）， 2013，26（02）:188-198.

［4］YANG Z Z，LIU D X，ZHANG X H.Study on Residual Strength of Pipe with Single Hemisphere Bottom Defect using FEM Analysis ［C］//Advanced Material Research Part 2:Advanced Manufacture Technology，314-316（2011）:1367-1371.

［5］杨专钊，刘道新，张晓化.含不深度球形缺陷钢管应力集中系数有限元求解［J］.机械工程材料，2013，37（08）:89-94.

［6］杨专钊，刘道新，张晓化.含腐蚀缺陷钢管剩余强度有限元模拟求解［J］.腐蚀科学与防护技术， 2013，25（04）:281-286.

［7］杨专钊，刘道新，张晓化.含平底型腐蚀缺陷钢管剩余强度有限元模拟及试验验证［J］.中国腐蚀与防护学报，2013，33（04）:339-346.

［8］CALEYO F，VELAZQUEZ J C，VALOR A，HALLEN J M.Probability Distribution of Pitting Corrosion Depth and Rate in Underground Pipelines:A Monte Carlo Study［J］.Corrosion Science， 2009，51（09）:1925-1934.

［9］TURNBULL A，MCCARTNEY L N，ZHOU S.A Model to Predict the Evolution of Pitting Corrosion and the Pit-to-crack Transition Incorporating Statistically Distributed Input Parameters［J］.Corrosion Science，2006，48（08）:2084-2105.

［10］ADIB-RAMEZANI H， JEONG J， PLUVINAGE G.Structural Integrity Evaluation of X52 Gas Pipes Subjected to External Corrosion Defects Using the SINTAP Procedure［J］.International Journal of Pressure Vessels and Piping，2006， 83 （06）:420-432.

［11］杨绪运，何仁洋，刘长征，等.腐蚀管道体积型缺陷评价方法［J］.管道技术与设备， 2009 （01）:47-04.

［12］MELIANI M H，MATVIENKO Y G，PLUVINAGE G.Corrosion Defect Assessment on Pipes Using Limit Analysis and Notch Fracture Mechanics［J］.Engineering Failure Analysis，2011，18（01）:271-283.

［13］ROLLINS B C，QUICKEL G T，BEAVERS J A，et al.Failure Analysis in Integrity Management Programs［A］.NACE Corrosion Conference ［C］//NACE Corrosion Conference， Nashville， Tennessee， USA: ［s.n.］，2007:07145.

［14］CHIODO M S G，RUGGIERI C.Failure Assessments of Corroded Pipelines with Axial Defects Using Stress-based Criteria:Numerical Studies and Verification Analyses［J］.International Journal of Pressure Vessels and Piping，2009， 86 （02-03）:164-176.

［15］MOUSTABCHIR H， AZARIZ， HARIRI S，et al.Experimental and Numerical Study of Stress-strain State of Pressurized Cylindrical Shells with External Defects［J］.Engineering Failure Analysis，2010，17 （02）:506-514.