质子-中子相互作用与壳模型配对近似

傅冠健 赵玉民

（上海交通大学 物理与天文系 上海 200240）

质子-中子相互作用与壳模型配对近似

傅冠健 赵玉民

（上海交通大学 物理与天文系 上海 200240）

质子-中子相互作用和质子-中子配对是原子核结构中有趣的问题。本文指出，经验上由结合能提取的质子-中子相互作用和壳模型计算得到的T=0质子-中子相互作用的计算结果很接近；计算中奇奇核和偶偶核的结合能应该附加一个额外项，这个额外项由质子-中子相互作用给出。自旋平行的质子-中子配对（角动量为9，同位旋为0）在96Cd的10+、12+、14+、16+、112+、114+和116+态以及92Pd原子核的10+和12+态中重要，而传统的SD配对近似对于10+和12+态的描述更合适。

质子-中子相互作用，T=0质子-中子配对，配对近似

原子核是由质子和中子构成的复杂多体系统，核子间的相互作用可以分为质子-质子相互作用(T=1, TZ=-1)、中子-中子相互作用(T=1, TZ=1)、以及质子-中子相互作用(T=0或1, TZ=0)，其中T和TZ分别是同位旋和同位旋三分量。人们对T=1相互作用（特别是同类核子间的相互作用）和同类核子的配对现象已有比较深入的认识。在这方面人们发展了很多理论模型，如辛弱数理论[1-2]、BCS理论[3-4]、相互作用玻色子模型[5]、壳模型配对近似理论[6-8]等，并取得了巨大成功。

人们很早就认识到质子-中子相互作用（尤其是T=0的部分）在原子核的形变、相变、集体运动等现象中起重要作用[9]，但是对质子-中子相互作用的理解仍然比较肤浅。由于理论计算上的困难，关于质子-中子配对（尤其是T=0配对）的研究比较少。2011年斯德哥尔摩研究组首次给出了92Pd原子核低能部分的能级图，并指出1g9/2轨道上自旋平行的质子-中子配对(J=9，T=0)在低激发态中的主导现象[10]。单轨道的壳模型理论计算表明[11]，这种新的配对机制在92Pd附近的原子核中确实重要，相互作用玻色子模型的计算也得到类似的结果[12]。

本文总结我们近年来关于质子-中子相互作用和自旋平行质子-中子配对方面的研究[13-14]。我们通过两种途径研究质子-中子相互作用：用结合能实验数据提取质子-中子相互作用，以及在壳模型框架下计算质子-中子相互作用。在原有的壳模型配对近似理论基础上引入了同位旋自由度[15]，在同位旋守恒的配对近似框架下研究自旋平行的质子-中子配对在96Cd和92Pd原子核低激发态中的贡献。

1 质子-中子相互作用

原子核中最后一个质子和最后一个中子之间的相互作用可以用四个相邻原子核结合能的双重差分来定义[16-17]，即：

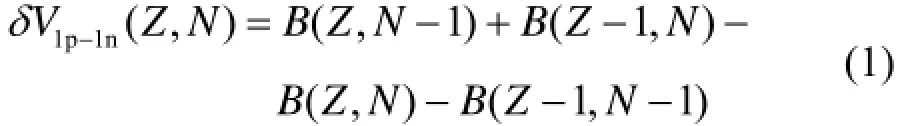
式中，Z是质子数，N是中子数，B是原子核结合能，这里的结合能取正值。δV1p-1n在重核区的系统性较好，在轻核区较差。从图1可以看到大部分δV1p-1n为负值，这表明质子-中子相互作用是吸引的。如果以双幻核作为核心把所有价核子之间的δV1p-1n累加起来，就得到总的质子-中子相互作用：

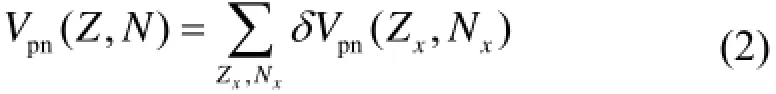
另一方面，我们在壳模型框架下采用USDB有效相互作用[18]计算sd壳原子核的基态波函数。USDB相互作用是sd空间壳模型计算中常用的相互作用之一。该相互作用包含3个单粒子能量参数和63个两体剩余相互作用矩阵元参数，这些参数基于核子-核子散射实验数据通过对sd壳原子核实验能级拟合得到。利用计算得到的基态波函数进一步计算T=0质子-中子相互作用和T=1质子-中子相互作用的期望值，分别记为

图2是壳模型计算得到的质子-中子相互作用与经验提取的质子-中子相互作用的比较。可以看到Vpn和VT=0在数值上非常接近，VT=1,TZ=0的强度比VT=0的强度小很多。这表明经验提取的质子-中子相互作用是壳模型框架下T=0质子-中子相互作用的一个好的近似。

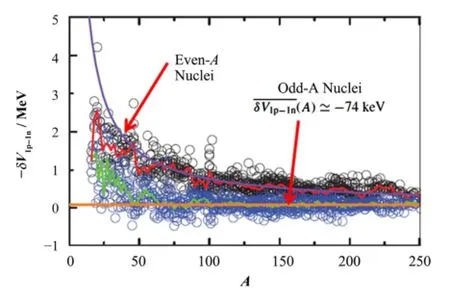
图1 原子核中最后一个质子和最后一个中子之间的经验相互作用Fig.1 Empirical proton-neutron interaction between the last proton and the last neutron.

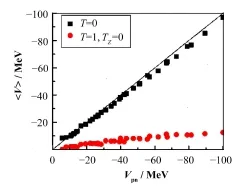
图2 sd壳原子核的T=0质子-中子相互作用和T=1质子-中子相互作用与经验质子-中子相互作用的比较Fig.2 Total isoscalar and isovector valence proton-neutron interactions vs. total empirical valence proton-neutron interaction for nuclei in the sd shell.

从图1中还看到一个有趣的现象，即偶质量数原子核的δV1p-1n强度明显大于奇质量数原子核的δV1p-1n强度。文献[19-20]曾提出质子-中子对力会导致奇奇核的结合能额外地增强，文献[21]进一步指出由质子-中子相互作用引起的组态混杂最终导致奇奇核的结合能额外地增强，这样可以解释δV1p-1n的奇偶性。然而文献[19]提出：假设偶偶核结合能额外地增强，也可以解释δV1p-1n的奇偶性。那么δV1p-1n奇偶性的真正原因是什么？是奇奇核的结合能额外地增强，还是偶偶核的结合能额外地增强，亦或是两者兼而有之？

为了研究这个问题，我们讨论Vpn。文献[9]指出Vpn近似与NpNn成正比，其中Np(Nn)是价质子（中子）数。对于一种同位素（假设质子数为Z），Vpn可以被近似表示为一个简单的线性公式Vpn≈aZN+bZ。如果假设Vpn精确符合上述线性关系，那么通过计算会发现δV1p-1n的奇偶性不复存在，正是因为Vpn对于线性关系的偏离才有δV1p-1n的奇偶性。

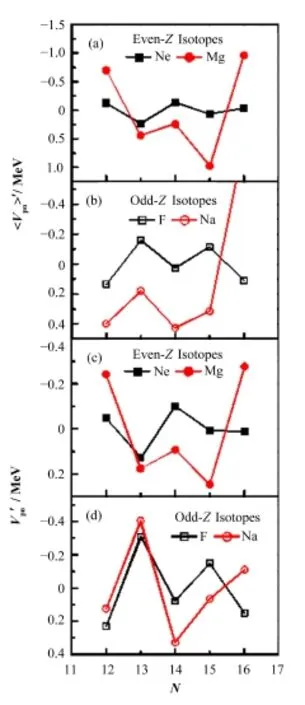
图3 V′ 和V′随中子数N的变化pn′pnFig.3 Vp′n and Vpn vs. neutron number N for a few sd shell nuclei.

2 自旋平行的质子-中子配对

在原有的壳模型配对近似理论基础上，我们发展了同位旋守恒的壳模型配对近似方法。这是目前研究同位旋标量的核子配对组态唯一的、直接的方法。假设双幻核外有2n个价核子，那么配对近似的组态空间由n个集体对耦合而成：

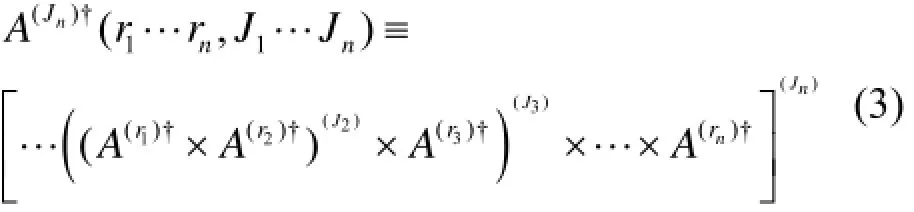
其中：

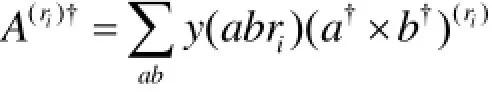
式中，A(ri)†表示一个角动量为Jri和同位旋为Tri的集体对；y(abri)是集体对结构系数。

我们利用这个方法研究96Cd和92Pd低激发态中的质子-中子配对(J=9, T=0)。我们把96Cd和92Pd看做双幻核100Sn以下、2p1/22p3/21f5/21g9/2壳层内的价空穴系统，将自旋平行的质子-中子配对记为A(9)，采用JUN45有效相互作用[22]计算并比较几种不同的组态空间下的T=0低激发态波函数。其中JUN45相互作用是2p1/22p3/21f5/21g9/2空间壳模型计算中常用的相互作用之一，该相互作用包含4个单粒子能量参数和133个两体剩余相互作用矩阵元参数，这些参数基于唯象相互作用通过拟合2p1/22p3/21f5/21g9/2壳原子核实验能级得到。

我们首先考察96Cd原子核。96Cd是双幻核100Sn以下的两质子空穴-两中子空穴系统。我们在以下4个壳模型空间下计算T=0态波函数：(1) 单轨道的1g9/2子空间；(2) 双轨道的2p1/21g9/2子空间；(3) 三轨道的2p1/22p3/21g9/2子空间；(4) 2p1/22p3/21f5/21g9/2全空间。我们发现对于不同角动量、能量最低的T=0态，空间(1)和空间(4)中计算得到的波函数重叠(overlap)平方约等于0.7，空间(2)和空间(4)中计算得到的波函数重叠平方同样约等于0.7。而对于绝大部分T=0低激发态，空间(3)和空间(4)中计算得到的波函数重叠平方大于0.9。这表明对于T=0低激发态，2p1/22p3/21g9/2子空间是2p1/22p3/21f5/21g9/2全空间好的截断近似。

我们在以下3个配对空间下计算96Cd原子核不同角动量、能量最低态的波函数：(1) T=0自旋平行的A(9)配对子空间；(2) T=1传统的SD配对子空间；(3) 2p1/22p3/21f5/21g9/2壳模型全空间。我们发现对于态，空间(1)和空间(3)中计算得到的波函数重叠平方大于0.5，A(9)配对子空间是壳模型全空间的有效截断近似；对于这两个态，传统的SD配对近似描述则更合适；空间(2)和空间(3)中计算得到的波函数重叠平方约等于0.9。

我们考察92Pd原子核，92Pd是双幻核100Sn以下的四质子空穴-四中子空穴系统。由于计算困难，很难在2p1/22p3/21f5/21g9/2全空间下进行研究，我们采用三轨道2p1/22p3/21g9/2空间。我们在以下3种配对空间下计算92Pd原子核10+和12+态的波函数：(1) A(9)配对子空间；(2) SD配对子空间；(3) 2p1/22p3/21g9/2壳模型空间。发现空间(1)和空间(3)中计算得到的波函数重叠平方约等于0.5，空间(2)和空间(3)中计算得到的波函数重叠平方大于0.8，SD配对近似比A(9)配对近似更合适。

3 结语

本文总结了我们近年来关于质子-中子相互作用方面的工作，利用原子核结合能实验数据提取经验质子-中子相互作用，并用壳模型计算T=0质子-中子相互作用和T=1质子-中子相互作用，指出经验质子-中子相互作用与T=0质子-中子相互作用的计算结果非常接近。计算表明奇奇核和偶偶核的结合能都有一个额外项，这个额外项由质子-中子相互作用给出，利用这个额外项我们可以自然地解释δV1p-1n的奇偶性。

研究自旋平行T=0质子-中子配对（记为A(9)配对）在96Cd和92Pd原子核低激发态中的贡献。在同位旋守恒的壳模型配对近似框架下，分别在2p1/22p3/21f5/21g9/2壳模型空间和配对截断子空间计算低激发态波函数。数值计算结果表明，A(9)配对在96Cd原子核的和1态以及92Pd原子核的态中重要，而传统的SD配对近似对于这两个原子核的态的描述则更合适。

1 Racah G. Theory of complex spectra II[J]. Physical Review, 1942, 62: 438-462

2 Racah G. Theory of complex spectra III[J]. Physical Review, 1943, 63: 367-382

3 Bardeen J, Cooper L N, Schrieffer J R. Microscopic theory of superconductivity[J]. Physical Review, 1957, 106: 162-164

4 Bardeen J, Cooper L N, Schrieffer J R. Theory of superconductivity[J]. Physical Review, 1957, 108: 1175-1204

5 Arima A, Iachello F. The interacting Boson model[J]. Advances in Nuclear Physics, 1984, 13: 139-200

6 Chen J Q. The Wick theorem for coupled fermion clusters[J]. Nuclear Physics A, 1993, 562: 218-240

7 Chen J Q. Nucleon-pair shell model: formalism and special cases[J]. Nuclear Physics A, 1997, 626: 686-714

8 Zhao Y M, Yoshinaga N, Yamaji S, et al. Nucleon-pair approximation of the shell model: unified formalism for both odd and even systems[J]. Physical Review C, 2000, 62: 014304

9 Casten R F. Nuclear structure from a simple perspective[M]. Oxford: Oxford University Press, 2000

10 Cederwall B, Algora A, Gadea A, et al. Evidence for a spin-aligned neutron-proton paired phase from the level structure of92Pd[J]. Nature, 2011, 469: 68-71

11 Qi C, Blomqvist J, Bäck T, et al. Spin-aligned neutron-proton pair mode in atomic nuclei[J]. Physical Review C, 2011, 84: 021301(R)

12 Zerguine S, van Isacker P. Spin-aligned neutron-proton pairs in N=Z nuclei[J]. Physical Review C, 2011, 83: 064314

13 Fu G J, Shen J J, Zhao Y M, et al. Regularities of proton-neutron interactions for nuclei in the sd shell[J]. Physical Review C, 2013, 87: 044309

14 Fu G J, Shen J J, Zhao Y M, et al. Spin-aligned isoscalar pair correlation in96Cd,94Ag, and92Pd[J]. Physical Review C, 2013, 87: 044312

15 Fu G J, Lei Y, Zhao Y M, et al. Nucleon-pair approximation of the shell model with isospin symmetry[J]. Physical Review C, 2013, 87: 044310

16 Zhang J Y, Casten R F, Brenner D S. Empirical proton-neutron interaction energies, linearity and saturation phenomena[J]. Physics Letters B, 1989, 227: 1-5

17 Basu M K, Banerjee D. Study of the neutron-proton interaction[J]. Physical Review C, 1971, 3: 992-997

18 Brown B A, Richter W A. New “USD” Hamiltonians for the sd shell[J]. Physical Review C, 2006, 74: 034315

19 Friedman W A, Bertsch G F. Neutron-proton pairing reexamined[J]. Physical Review C, 2007, 76: 057301

20 de-Shalit A. Interpretation of regularities in neutron and proton separation energies[J]. Physical Review, 1957, 105: 1528-1530

21 Gao Z C, Chen Y S. Enhancement of the n-p interaction in odd-odd nuclei[J]. Physical Review C, 1999, 59: 735-739 22 Honma H, Otsuka T, Mizusaki T, et al. New effective interaction for f5pg9-shell nuclei[J]. Physical Review C, 2009, 80: 064323

CLCTL11, O571.2

Proton-neutron interactions and nucleon-pair approximation

FU Guanjian ZHAO Yumin
(Department of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China)

Background: Nucleon-pair correlations play an important role in low-lying states of atomic nuclei. Purpose: The aim is to study empirical proton-neutron interactions and investigate the contribution from spin-aligned proton-neutron pairs (with spin 9 and isospin 0) in low-lying states of96Cd and92Pd. Methods: The empirical proton-neutron interaction is obtained by using nuclear binding energies of a few neighboring nuclei and the nuclear shell model. The contribution from spin-aligned proton-neutron pairs in the shell model wave functions is evaluated by using the nucleon-pair approximation with isospin symmetry. Results: The empirical proton-neutron interaction is reasonably consistent with isoscalar interactions calculated by using the shell model. There exists an additional binding energy in both even-even and odd-odd nuclei originated from proton-neutron interactions. Spin-aligned isoscalar pairs play an important role in theand1 states of96Cd and thestates of92Pd. For thestates, the conventional isovector SD pairs are more relevant. Conclusion: Both isoscalar and isovector nucleon pairs play an important role in low-lying states of N=Z nuclei. This is a consequence of nonorthogonality feature of nucleon-pair basis.

Proton-neutron interaction, T=0 proton-neutron pair, Nucleon-pair approximation

TL11，O571.2

10.11889/j.0253-3219.2014.hjs.37.100502

国家自然科学基金(No.11225524)和973项目(No.2013CB834401)资助

傅冠健，男，1988年出生，2010年毕业于上海交通大学，现为该校在读博士研究生，研究领域为原子核结构

赵玉民，E-mail: ymzhao@sjtu.edu.cn

2014-04-30，

2014-05-28