一类高阶线性微分方程解的增长级

钟文波，易才凤

(江西师范大学数学与信息科学学院，江西南昌330022)

0 引言和主要结果

本文假定读者熟悉Nevanlinna值分布的基本理论和标准记号［1-2］，用T(r，f)表示亚纯函数f的特征函数，ρ(f)表示亚纯函数f的增长级，μ(f)表示f的下级，n(Ω(θ-ε，θ+ε，r)，f=a)表示f-a在角域Ω(θ-ε，θ+ ε，r)={z:θ- ε＜argz＜ θ+ ε，内的零点(计重数)个数.

定义1［3］设f(z)是λ(0＜λ≤∞)级亚纯函数，1条从原点出发的射线argz=θ称为f的1条λ级Borel方向，如果

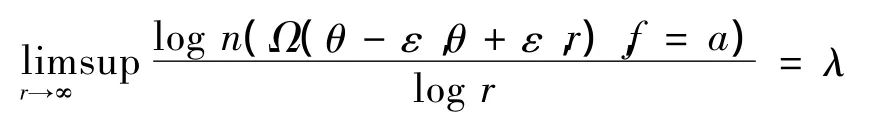
至多除去2个例外的复数a.

定义2［4］设f(z)是下级为μ(f)(0＜μ(f)＜∞)的亚纯函数，λ为一有限常数且满足μ(f)≤λ≤ρ(f)，1条从原点出发的射线argz=θ称为f的1条级≥λ的Borel方向，如果

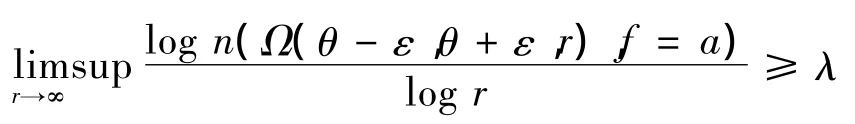
至多除去2个例外的复数a.

众所周知，关于2阶线性微分方程

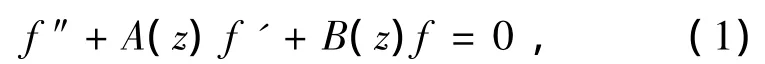
当A(z)，B(z)是整函数时，方程(1)的解都是整函数，并且如果B(z)是超越的，而f1，f2是方程(1)的2个线性无关解，则f1，f2中至少有1个是无穷级.一个很自然的问题:当A(z)，B(z)满足什么条件时，会使得方程(1)的所有非零解都是无穷级?1988年，G.G.Gundersen在文献［5］中假定A(z)，B(z)为整函数并满足ρ(A)＜ρ(B)，以及 1991年 S.Hellerstein等在文献［6］中假定A(z)是多项式，B(z)是超越的或ρ(B)＜ρ(A)≤1/2，在这些条件下证明了方程(1)的所有非零解均为无穷级.关于方程解的无穷级讨论，还有一些有趣的结论，详见文献［7-10］.

熟知，亏值和Borel方向是亚纯函数Nevanlinna值分布理论中的2个不同概念，而杨乐和张广厚却惊奇地发现2者之间有直接联系，即下面定理A.

定理A 假设f是具有有限下级μ(μ＞0)的整函数，q为f的级≥μ的Borel方向的条数，p为f的有限亏值的个数，则p≤q/2.

本文中称定理A中的“p≤q/2”为杨-张不等式，如果f满足极端情况p=q/2，则称f满足杨-张不等式的极端情况.2013年，龙见仁等在文献［11］中，运用杨-张不等式的极端情形进一步研究了方程(1)的相关问题，得出下面的结论.

定理B 假设A(z)是满足杨-张不等式的极端情况p=q/2的整函数，B(z)为一超越整函数且ρ(A)≠ρ(B)，则方程(1)的所有非零解f都具有无穷级.

定理C 设A(z)是满足杨-张不等式的极端情况p1=q1/2的整函数，B(z)也满足杨-张不等式的极端情况p2=q2/2，若有下列条件之一成立:

(i)q1≠q2;

(ii)q1=q2且A(z)的Borel方向的集合不同于B(z)的Borel方向的集合，则方程(1)的所有非零解f都具有无穷级.

本文主要从杨-张不等式的极端情况来研究高阶线性微分方程

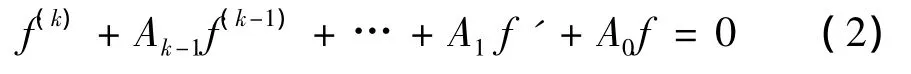
解的增长性，证明了以下结论.

定理1 假设Aj(z)(j=0，1，…，k-1)为整函数，其中存在1个Ai(z)(i≠0)满足杨-张不等式的极端情况 p=q/2，ρ(Ai)≠ρ(A0)，且ρ(Aj)＜ρ(A0)(j≠i)，则方程(2)的所有非零解f都具有无穷级，且超级满足

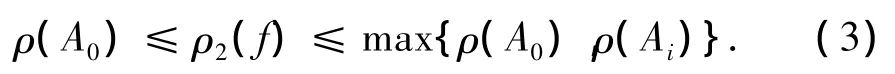
定理2 假设Aj(z)(j=0，1，…，k-1)为整函数，其中存在1个Ai(z)(i≠0)满足杨-张不等式的极端情况p1=q1/2，A0(z)也满足杨-张不等式的极端情况 p2=q2/2，且ρ(Aj)＜ρ(A0)(j≠ i)，若下列条件之一成立:

(i)q1≠q2;

(ii)q1=q2，Ai(z)的Borel方向的集合不同于A0(z)的Borel方向的集合，则方程(2)的所有非零解f都具有无穷级，且超级满足(3)式.

注1 在定理1和定理2 中，超级均满足(3)式，进一步，如果ρ(Ai)≤ρ(A0)，则ρ2(f)=ρ(A0).

1 引理

引理1［12］设Aj(z)(j=0，1，…，k-1)是整函数，且ρ(Aj)＜ρ(A0)＜∞(j=1，…，k-1)，则高阶线性方程(2)的所有非零解f具有无穷级.

引理2［13］假设f满足杨-张不等式的极端情况，则μ(f)=ρ(f).进一步，对于每1个亏值ai(i=1，…，p)，都存在 1 个相应的角域 Ω(θki，θki+1)={z:θki＜argz＜θki+1}，使得对于每个ε＞0和z∈Ω(θki- ε，θki+1+ ε，r，∞)都有

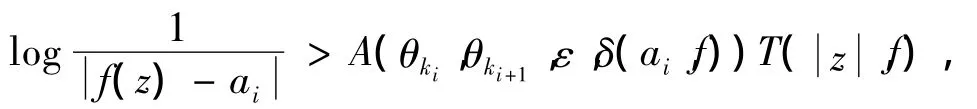
其中A(θki，θki+1，ε，δ(ai，f))是仅依赖于 θki，θki+1，ε和 δ(ai，f)的正常数.

引理3 假设f满足杨-张不等式的极端情况，并且 ∃θ∈ Ω(θj，θj+1)(1≤j≤q)，使得

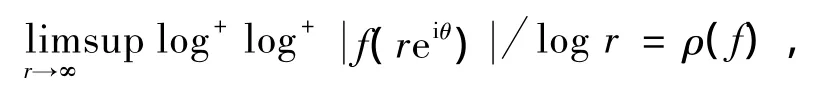
引理4［14］设f(z)是开平面上的超越亚纯函数，Γ={(k1，j1)，(k2，j2)，…，(kq，jq)}是由不同整数对组成的有限集合，满足ki＞ji≥0(i=1，2，…，q)，又设α(α＞1)是给定的实常数及ε＞0为任意给定的正数，则存在零测度集E1⊂［0，2π)和仅依赖于Γ和α的常数C，使得如果φ0∈［0，2π)E1，则存在常数R0=R0(φ0)＞1，对满足argz=φ0及的所有的z及所有的(k，j)∈Γ，都有

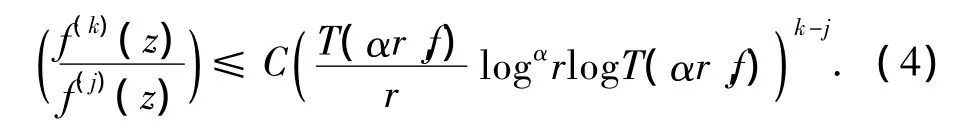
特别地，当f(z)的级ρ(f)=ρ＜∞ 时，(4)式可由下面的(5)式代替:

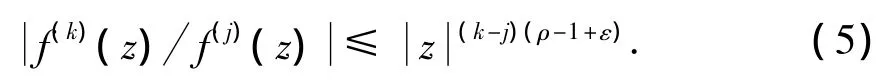
引理5［15］设f(z)是具有无穷级的整函数，其超级ρ2(f)=ρ，令υ(r)为f的中心指标，则

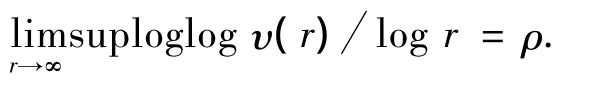
引理6 设Aj(z)(j=0，1，…，k-1)满足定理1(或定理2 )的条件，且方程(2)的非零解f具有无穷级，则超级ρ2(f)≤max{ρ(A0)，ρ(Ai)}.

证由Wiman-Valiron理论可知，存在1个具有有穷对数测度的集合E2⊂(1，+∞)，使得当z满足时，有

记ρ1=max{ρ(A0)，ρ(Ai)}，显然ρ(Aj)≤ρ1(j=0，1，…，k-1).∀ε ＞ 0，当 r充分大时，有

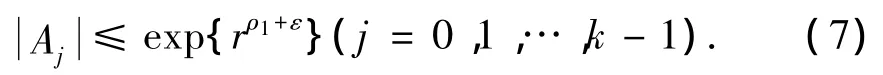
方程(2)可变形为

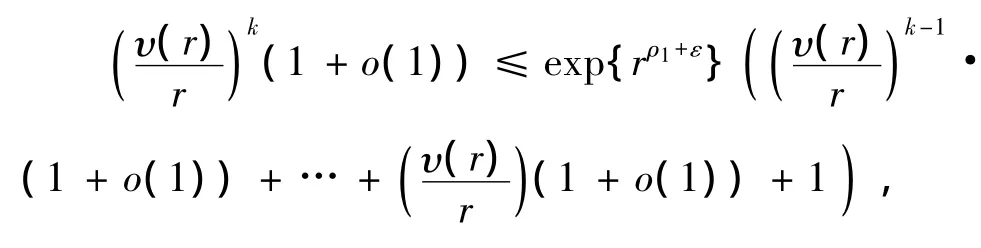
即

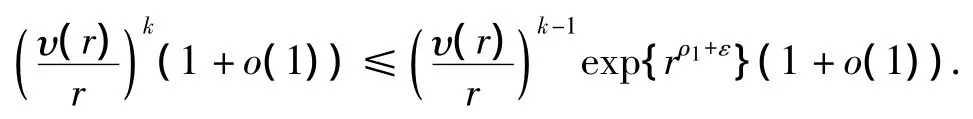
由引理5和ε的任意性得

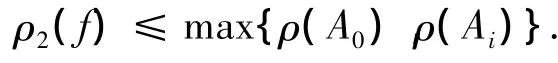
2 定理的证明

由定理1的假设，Ai(z)满足杨-张不等式的极端情况，不妨设ai(i=1，…，p)是Ai(z)的所有有限亏值，argz= θj(j=1，2，…，2p)是Ai(z)的ρ(A0)级Borel方向，故存在2p个角域argz＜θj+1}(j=1，…，2p)，由引理 2、引理 3 和Borel方向的定义可以知道Ai(z)有如下性质:

在每个角域Sj中，或者存在一些ai，使得当z∈Ω(θj- ε，θj+1+ ε，r，∞)时，有

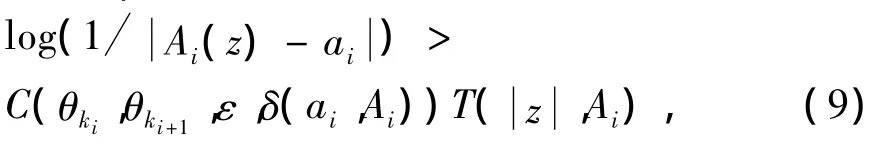
其中 C(θki，θki+1，ε，δ(ai，Ai))是仅依赖于 θki，θki+1，ε和 δ(ai，Ai)的正常数;或者 ∃θ∈ Sj，使得

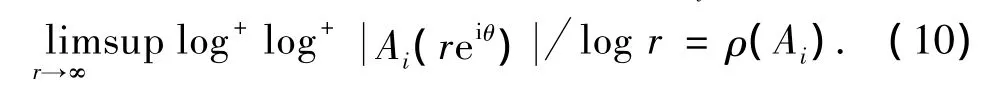
为方便起见，记 C(θki，θki+1，ε，δ(ai，f))为 C，注意到若存在某些ai在Sj中满足(9)式，则在Sj-1和Sj+1中∃θ使得(10)式成立;若∃θ∈Sj满足(10)式，则分别有某些ai或ai'在Sj-1和Sj+1上满足(9)式.

不失一般性，假设在S1中∃argz=θ满足(10)式，故在S3，S5，…，S2p-1中均存在相应的1条射线满足(10)式.由引理3可知，这些角域的张角均为πρ(Ai).

下面分2种情形讨论.

情形1 当ρ(A0)≥1/2时，由Phragman-lindelof定理可知，存在1个角域 Ω(α，β)(0≤α＜β＜2π)，使得 β-α≥ πρ(A0)，并且对于所有的argz= θ(α＜ θ＜ β)，有

调查表明，学生在学完《统计学原理》课程后，较少运用统计的相关知识，其比例高达73.4%，超总体的2/3之多；能够熟练运用统计知识的学生仅有26.7%。这种现象在一定程度上说明了，学生没有学以致用，缺乏应用所学知识去解决实际问题的能力。

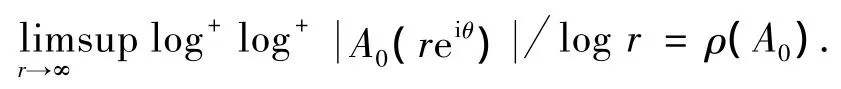
注意到ρ(Ai)＞ρ(A0)，不难知道存在角域Ω(α'，β')(α＜ α'＜ β'＜ β)和aj0，使得 ∀θ(α'≤θ≤β')有

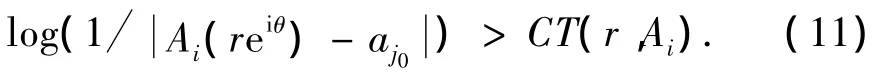
由引理4可知，∃θ0(α'≤θ0≤β')和R1＞ 0，使得对 j=1，…，k，当 r ＞ R1时，有

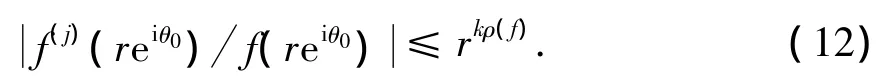
又由于

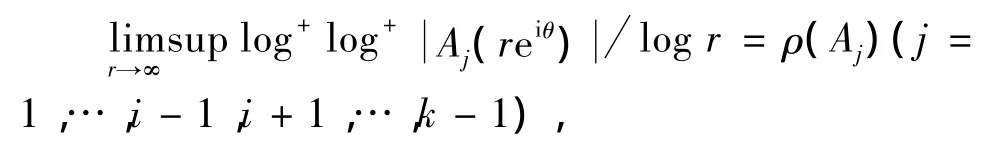
则∀ε ＞0，∃R2＞0，对所有的r＞R2，有

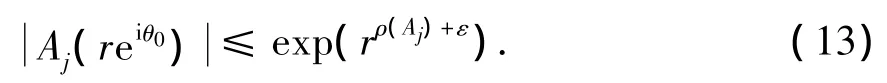
记 l=max{ρ(Aj)}(j≠ i)，显然 l＜ρ(A0).

注意到

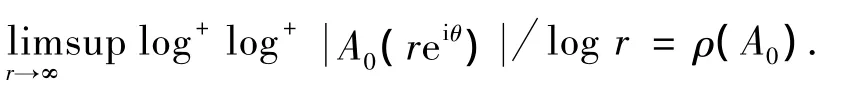
因此存在1列{rn}(ρ(A0)-l)2)，有

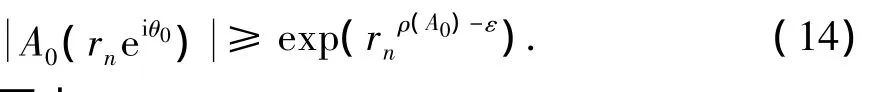
再由

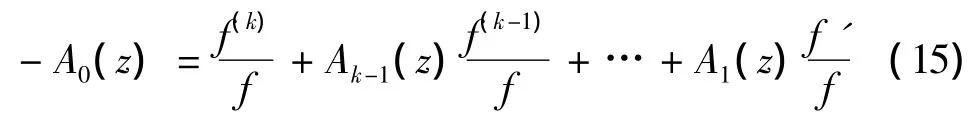
及(11)～(14)式可知

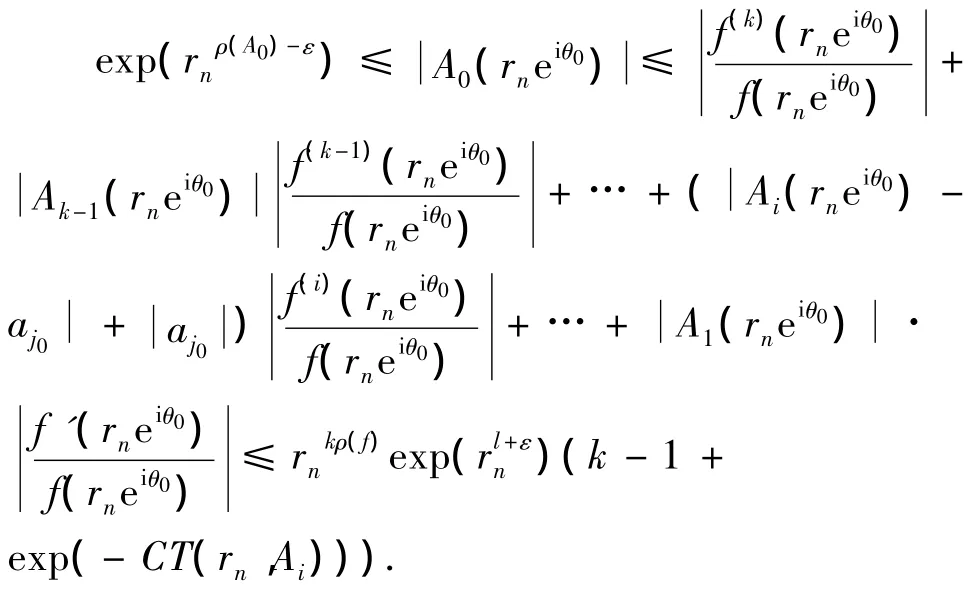
当n充分大时，上式显然矛盾.

情形2 当ρ(A0)＜1/2时，由于A0(z)是1个超越的整函数，由文献［16-17］的结果可知，∀θ∈［0，2π)，有

类似于情况1的讨论，可得到矛盾.

综合情形1和情形2可知，已经证明了方程(2)的所有非零解均具有无穷级，由引理6可知ρ2(f)≤max{ρ(A0)，ρ(Ai)}.下面证明ρ2(f)≥ρ(A0)，也分2种情形讨论.

(i)ρ(A0)≥1/2.

由引理4可知，存在1个零测度集合E1⊂［0，2π)和2个常数B ＞ 0，R3＞ 0，当及argz= θ∉E1时，有

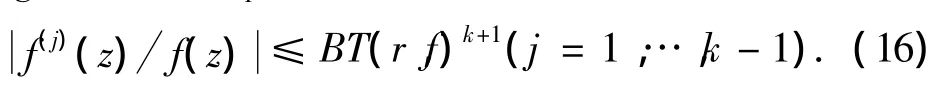
对每个ε＞0(0＜ε＜(ρ(A0)-l)2)，取满足(14)式的1 列{rn}，当 z=rneiθ1，且rn＞max(R2，R3)，θ1∈ Ω(α'，β')-E1时，有(11)、(13)～(14)和(16)式成立，将其代入(15)式，得

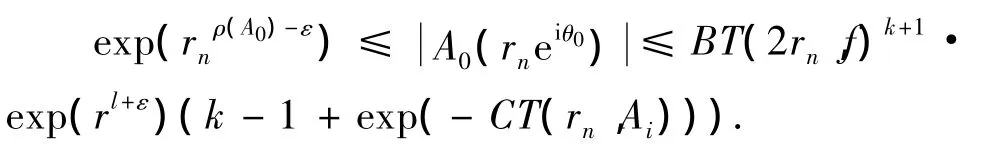
由ε的任意性可知ρ2(f)≥ρ(A0).

(ii)当ρ(A0)＜1/2时，类似于(i)的证明方法可得结论成立.

定理2 的证明首先考虑Ai(z)，A0(z)满足条件(i)的情形，若ρ(Ai)≠ρ(A0)，则由定理1可知方程(2)的所有非零解f满足ρ(f)=∞，且超级满足(3)式.下面考虑ρ(Ai)=ρ(A0)=ρ的情况，将其分为2种情形q1＜q2和q1＞q2.

情形1 当q1＜q2时，从引理2和引理3可知，存在q2/2个张角为π/ρ的角域，使得

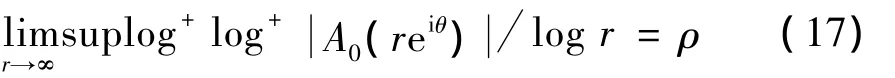
并有q1/2个张角为π/ρ的角域，使得

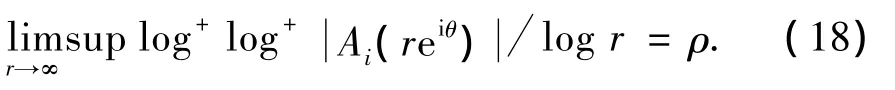
由q1＜q2不难看出，∃α，β(0＜α＜β＜2π)，使得∀θ∈(α，β)，Ai(z)有界，而A0(z)满足(17)式，类似证明定理1的方法可知，方程(2)的每个非零解f具有无穷级，且超级满足(3)式.

情形2 当q1＞q2时，也存在1个角域Ω(α，β)，使得Ai(z)有界，而A0(z)满足(18)式，也用类似证明定理1的方法可得结论.

当Ai(z)，A0(z)满足条件(ii)时，可看出存在1个角域，使得在该角域内Ai(z)有界，而A0(z)满足(17)式，类似于前面的讨论，同样可得到结论.

［1］Hayman W K.Meromorphic function［M］.Oxford:Clarendon Press，1964.

［2］杨乐.值分布论及其新研究［M］.北京:科学出版社，1982.

［3］张广厚.整函数和亚纯函数理论［M］.北京:科学出版社，1986.

［4］Yang Le.Deficient values and angular distribution of entire functions［J］.TransAmer Math Soc，1988，308(2):583-601.

［5］Gundersen G G.Finite order solution of second order linear differential equations［J］.TransAmer Math Soc，1988，305(1):415-429.

［6］Hellerstein S，Miles J，Rossi J.On the growth of solutions of f″+g f'+hf=0 ［J］.TransAmer Math Soc，1991，324(2):693-705.

［7］Chen Zongxuan.The growth of solutions of f″+e-zf'+Q(z)f=0 where the order(Q)=1［J］.Science in China:A，2002，45(3):290-300.

［8］刘旭强，易才风.关于2阶线性微分方程f″+A f'+Bf=0解的增长性［J］.江西师范大学学报:自然科学版，2013，37(2):171-174.

［9］石磊，易才风.一类高阶线性微分方程解的增长性［J］.江西师范大学学报:自然科学版，2012，36(3):230-233.

［10］Wu Pengcheng，Zhu Jun.On the growth of solutions to the complex differential equation f″+A f'+Bf=0［J］.Science China:Mathematics，2011，54(5):939-947.

［11］Long Jianren，Wu Pengcheng，Zhang Zheng.On the growth of solutions of second order linear differential equations with extremal coefficients［J］.Acta Mathematica Sinica，English Serier，2013，29(2):365-372.

［12］Chen Zongxuan，Gao Shian.The complex oscillation theory of certain non-homogemeous linear differential equations with transcendental entire coefficients［J］.Journal of MathematicalAnalysis andApplications，1993，179(2):403-416.

［13］ Wu Shengjian.Some results on entire functions of finite lower order［J］.Acta Math Ematica Sinica，English Series，1994，10(2):168-178.

［14］Gundersen G G.Estimate for thelogarithmic derivative of ameromorphic function ［J］.J London Math Soc，1988，37(1):88-104.

［15］Chen Zongxuan，Yang Chongjun.Quantitative estimates on the zeros and growth of entire solutions of linear differential equations［J］.ComplexVariables，2000，42(1):119-133.

［16］Barry P D.On a theorem of besicovitch［J］.Quant J Math Oxford Ser，1963，14(2):293-302.

［17］Chen Zongxuan，Yang Chongjun.Some further results on the zeros and growths of entire solutions of second order linear differential equations［J］.Kodai Math J，1999，22(2):273-285.