悬链线几何性质的研究

谢 菲，孙明珠

悬链线问题的提法：设A和B是铅垂面上两个等高点，一条柔软的绳索挂在 A、B上（图1），在所有连接A、B的平面曲线中，求出一条曲线，使得其重力势能最小.悬链线的方程：

本文将研究悬链线的一些几何性质，诸如面积、旋转体体积、曲率中心、渐屈线等.

图1 悬链线

一、面积与面积形心

图2 悬链线和直线围成的面积

单单由悬链线构不成面积，还需要和其他直线或曲线结合才能围成面积.比如，图2所示，求悬链线和x轴、y轴以及x=x1所围成的图形之面积S1，或求悬链线和y轴、y=y1所围成的图形之面积S2.下面就分别推导这两种情况下的面积公式.

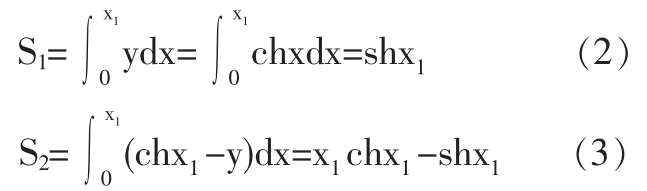
形心又称作面积中心，坐标公式为

据此，对于S1有形心坐标的积分表达式：

二、旋转体体积

图3 S1绕y轴旋转一周

图4 S1绕x轴旋转一周

1.求S1绕y轴旋转一周所形成的旋转体（图3）的体积Vy由求旋转体体积的圆筒微元法Vy=Σ2πxiyiΔxi，有积分表达式：

2.求S1绕x轴旋转一周所形成的旋转体（图4）的体积Vx由求旋转体体积的切片微元法Vx=Σπyi2Δxi，有积分表达式：

3.第二古鲁金定理：平面图形绕与其不相交的轴旋转一周所得立体的体积，等于平面图形的面积与形心绕同一转轴旋转的周长之积.即 Vx=2πycS，Vy=2πxcS.

对于S1，我们验证一下第二古鲁金定理的正确性。

这恰好等于式（7）和式（6）得到的结果.于是我们可以推出S2的形心坐标：

谢菲/天津工业大学理学院讲师（天津300387）；孙明珠/天津工业大学理学院教授 （天津300387）。

读者可以验证：对于面积S2，用积分表达式求得的形心坐标，结果与此完全相同.

三、曲率半径

四、曲率中心与渐屈线

图5 曲率中心与渐屈线

图中M为悬链线上的一点，K为M点的曲率中心，ρ为曲率半径.根据曲率中心的定义，曲率半径ρ与M点的切线垂直.M点的切线斜率为y′=tanα=shx

所以

设 K 点的坐标为（x1，y1），M 点的坐标为（x，y），则有

图5中曲率半径ρ的直线方程为

据此，用Matematica软件通过下面一段程序画出悬链线的渐屈线如图5所示.

渐屈线像一个“V”字.

[1]孙明珠等.游戏中的数学文化[M].北京：国防工业出版社，2011.

[2]同济大学数学教研室.高等数学（第六版）[M].北京：高等教育出版社，2007.