利用改进CV模型连续水平集算法的核磁共振乳腺图像分割
2014-01-17王芳梅范虹YiWANG
王芳梅,范虹,Yi WANG
(1.陕西师范大学计算机科学学院,710062,西安;2.康奈尔大学生物医学工程系,14853,美国纽约伊萨卡)
随着X射线钼靶摄影、超声成像、X射线计算机断层摄影(computerized tomography,CT)、核磁共振成像(magnetic resonance imaging,MRI)等影像技术的不断发展,乳腺疾病的计算机临床辅助诊断技术得到了广泛应用。动态增强核磁共振成像(Dynamic Contrast-Enhanced Magnetic Resonance Imaging,DCE-MRI)是通过静脉注射对比剂无损地评价组织和肿瘤血管特性的一种功能性成像方法[1]。MRI因具有无创、多层、多参数、多序列和较高软组织分辨能力的特性,因而成为诊断乳腺疾病的首选方式之一,MR乳腺图像分割在乳腺疾病的诊断和量化分析中起着越来越重要的作用。但是,由于MR乳腺图像存在信息量大、噪声复杂、边界模糊、灰度不均匀等现象,使得乳腺活检图像的分割工作仍然存在一定的困难。现有的医学图像分割方法主要有阈值法、区域增长法、特征聚类法和主动轮廓法。
属于主动轮廓模型范畴的水平集方法[2]因能够直接获取闭合分割线、并能有效处理图像分割过程中的拓扑问题而赢得了关注,目前已得到了大量应用[3-5]。Ball等人利用水平集方法实现了乳房X射线图像分割,通过利用基于Chan-Vese(CV)模型的离散水平集方法引入目标的区域特征信息,解决了无明显边界信息的目标分割难题,同时解决了传统CAD系统仅能处理边缘分析问题的局限性[6]。Lin等人提出了结合高斯金字塔的多分辨率水平集框架,解决了模糊超声图像难分割的问题[7]。郭礼华等人利用一种基于高斯矢量场(GVF)的多分辨率水平集图像分割方法,实现了实际场景的人脸提取,通过引入GVF模型,扩大图像力的作用范围,有效解决了弱边界问题[8]。余瑞星等人利用多分辨率水平计算法,实现了海岸线SAR图像的分割[9]。
为了进一步研究MR乳腺图像分割,根据传统CV模型[10],本文提出一种基于改进CV模型的连续水平集算法,利用B样条基函数[11]将传统离散水平集函数表示成连续形式,用解决B样条空间的变分问题代替水平集函数更新的计算问题,通过在CV模型中引入偏移量构造新的图像分割能量模型,可以在图像分割过程中避免水平集函数的重新初始化和分割陷入局部极小值现象,提高分割效率,并有效抑制噪声,从而获得准确、稳定的MR乳腺图像分割结果。
1 传统水平集方法
1.1 离散水平集函数的表示
假设二维平面曲线为C(r,t),其中r为弧长参数,t为时间参数,它对应的三维水平集函数为φ(x,y,t),则曲线可以通过零水平集函数表示为:通过符号距离函数(signed distance function,SDF)表示的水平集函数为

式中:d(x,y)是空间区域中一点到曲线C的距离,点(x,y)在曲线C的内部时取正号,在外部时取负号。符号距离函数的取值示意图见图1。

图1 符号距离函数取值示意图
1.2 CV能量函数
在 Mumford-Shah模型[12]的基础上,Chan和Vese提出了Chan-Vese(CV)模型。该模型是基于区域信息的图像分割能量模型,既可以检测出有梯度信息的目标边界,也可以检测出无梯度信息的目标边界;同时,不仅可以分割出连续边界的图像,还可以分割出不连续边界的图像。用分段常量表示图像,假设c1、c2为常量,分别表示图像目标和背景区域,则CV能量函数的表达式为

式中:μ≥0、ν≥0、λ1>0、λ2>0均为常数系数;第1项和第2项分别是长度、面积规则项;后2项驱动闭合曲线项的目标边界演化。u0:Ω→R是原图像区域,初始轮廓线用C表示,c1、c2是通过给定闭合曲线C内、外区域的灰度均值表示的。
2 基于改进CV模型的连续水平集算法的实现
2.1 连续水平集函数的表示
B样条是一种简单的基函数,整数结点处的函数值可以表示该点处基函数的系数。水平集函数可用B样条基函数的线性组合形式表示为

式中:βn(·)是n阶B样条基函数;h为空间尺度;B样条的结点是由图像定义的空间域Ω中的网格结点;c(i,j)表示 B样条基函数的系数集。
由于水平集函数是由B样条基函数的线性组合表示的,因此,水平集函数不断更新的过程可以用简单的卷积操作实现。水平集的每一步演化都可以视为经过B样条核函数滤波作用的结果,该滤波器具有较高的抗噪性,可保证在图像分割中对噪声的抑制作用。
2.2 基于改进CV模型的图像分割模型
Chan和Vese在Mumford-Shah能量式基础上改进的图像分割方法——CV模型结合了图像的全局灰度统计信息,通过极小化水平集函数的能量函数来达到图像分割的目的。为了避免在求解函数极小值过程中出现局部极小值的现象,Chan和Vese引入了Heaviside函数,但是却存在难以设置曲线演化停止条件的困难。
为了实现乳腺MR图像的分割,本文对CV模型中的拟合项引入偏移量得到α-CV模型,并将其作为能量函数。将此能量函数用于分割实验,可以去除局部极小值现象并设置有效的曲线演化停止条件。能量函数的表达式为

为了求式(5)的极小值,需利用关于水平集函数的梯度下降流方程式

式中:α是任意小的非负常量;Ω是图像u0的定义域。关于水平集函数φ的能量函数式的极小化得到的零水平集将目标区域与背景区域分割成2部分。通过式(5)等号右侧第2项的负号可见,该能量泛函明显区别于CV模型。通过扩大水平集函数φ的比例,使得能量泛函值可以不依赖于φ值符号的改变而变化,从而避免了能量泛函值陷入局部极小值现象。式中修改Heaviside函数为位移Heaviside函数,用于控制决定能量泛函值变化的水平集函数值的范围。当唯一变量α=0时,能量项中的第1项仅在水平集函数为正值的情况下才发生变化,而能量项中的第2项仅在水平集函数为负值的情况下才发生变化。即使u0(X)≠c1,u0(X)≠c2,当求能量项的极小值时,会使得水平集函数的值趋向于0,从而发生曲线局部收敛。为了避免这种现象,本文引入带有位移量α的Heaviside函数,具体作用如下:
(1)控制水平集函数的演化,根据当前水平集函数确定能量函数的极小化,从而达到全局极小值的目的;
(2)制约水平集函数的取值,从而保证求函数极小值的过程能得到稳定解。
当u0(X)≠c1、u0(X)≠c2时,水平集函数应该趋于某个非零值,这样零水平集才能实现图像域中目标与背景的分离。为了达到这一目的,将Heaviside函数按照变量α进行位移。对式(6)仅保留第1项,对能量泛函极小化,当任意时刻φ>-α时,φ值趋于-α;对式(6)仅保留第2项,对能量泛函极小化,当任意时刻φ<α时,φ值趋于α;当这2项全部保留时,在水平集函数值满足-α≤φ≤α的图像域中,由|u0-c1|2、|u0-c2|2这2项的取值决定水平集函数φ是否趋于α或-α,由此达到期望的分割目的。显然,通过式(5)可得:当能量泛函被极小化时,任意处于|u0-c1|2<|u0-c2|2图像域中的像素点都被划分到区域r:φ(r)=-α中;相反,任意处于|u0-c1|2>|u0-c2|2图像域中的像素点都被划分到区域r:φ(r)=α中。
假设图像定义域为2相,且满足R1∈Ω:|φ(R1)|>α和R2∈Ω:|φ(R2)|≤α。为了方便理解,取λ1=λ2=1,定义能量泛函积分的表达式为

可见式中φH(α+φ)和φH(α-φ)是由水平集控制的,即|u0-c1|2、|u0-c2|2仅依赖于零水平集。当在R1中时,有Γ(φ)=|u0-c1|2φ,Γ(φ)随着φ的减小而减小,直到水平集到达目标边界,即φ=α时,Γ(φ)达到稳定状态;相反,当在R2中时,Γ(φ)随着φ的减小而减小,直到水平集到达目标边界,即φ=-α时,Γ(φ)达到稳定状态。因此,在式(6)的作用下,所有满足|φ|>α区域中的水平集随着|φ|的减小而演化一次,并且控制水平集函数处于-α≤φ≤α区域。
3 实验结果与分析
3.1 仿真数据实验结果与分析
为了验证算法的有效性,在Matlab(R2011b)编程环境下进行仿真实验,实验平台为 Windows XP,CPU为Pentium 4,主频为3.0GHz,内存为1GB。图像大小为256×256像素,灰度级为256。迭代步长为3。为了进一步简化正则化函数δ(·),参数ε取1。
分割结果如图2所示:图中第1列是原始图像,第2列是加入均值和方差分别为0和0.01的高斯噪声后的图像(称为含噪图像Ⅰ),第3列是加入均值和方差分别为0和0.1的高斯噪声后的图像(称为含噪图像Ⅱ);第1行是分割前的图像,第2行是使用传统基于CV模型的离散水平集算法(以下简称传统算法)分割后的图像(ν=255×255,迭代100次),第3行是在h=2、ν=0、迭代3次条件下使用本文提出的基于改进CV模型的连续水平集算法(以下简称本文算法)的分割结果,第4行是在h=3、ν=0、迭代3次条件下采用本文算法的分割结果。

图2 数字图像分割对比图
从抗噪性能方面看,由于传统离散水平集算法对曲率的高度依赖,使得平滑噪声的效果存在一定的限制,信噪比越低的图像平滑效果越差,对噪声敏感性较强。本文算法可以有效降低对噪声的敏感性,和传统离散水平集方法相比,即使分割较低信噪比的图像,也能得到较好的分割效果。由图2第3行和第4行的分割结果可以看出,文中所选基函数参数h的取值对分割效果的影响呈正相关,即在相同条件下,h取值越大对噪声的平滑效果越好,得到的图像分割效果越理想。
从分割精度方面看,由图2第2、第3和第4行相应列的分割结果可以看出:传统CV模型存在容易陷入局部极小值的现象,得不到全局图像分割结果;本文采用的改进CV模型拟合项的能量函数可以避免出现局部极小值现象,得到较好的全局图像分割结果,并且在同样的条件下达到有效收敛,完成曲线演化,得到全局目标轮廓线。
3.2 临床数据实验结果与分析
为了实现对MR乳腺图像的分割,本节将对4个病人的临床实验数据(13个)用基于CV模型的离散水平集算法和本文算法进行分割对比,通过仿真实验证明本文算法分割图像的有效性。
实验中所用的数据是由康奈尔大学医学成像实验室提供、并且由病人授权本论文使用的乳腺临床MRI数据,图像是通过使用T1加权获得的带有饱和脂肪梯度回波力的矢状面切片序列,采样间隔时间为8.1ms,回波时间为4ms,翻转角度为30°。成像所用仪器为德国埃朗根西门子公司的具有专用双乳房线圈的1.5T全身核磁共振成像系统,病人在成像时处于俯卧姿势。
图3~图5是针对3位病人在相同采样间隔时间下获取的冠状面、矢状面成像的12例乳腺MR图像,采用本文基于改进CV模型的连续水平集算法和传统的基于CV模型的离散水平集算法的分割结果对比,图像大小为512×512像素,平均灰度级分别为1 125、2 215和667。水平集函数参数h=3,ν=0,迭代10次。
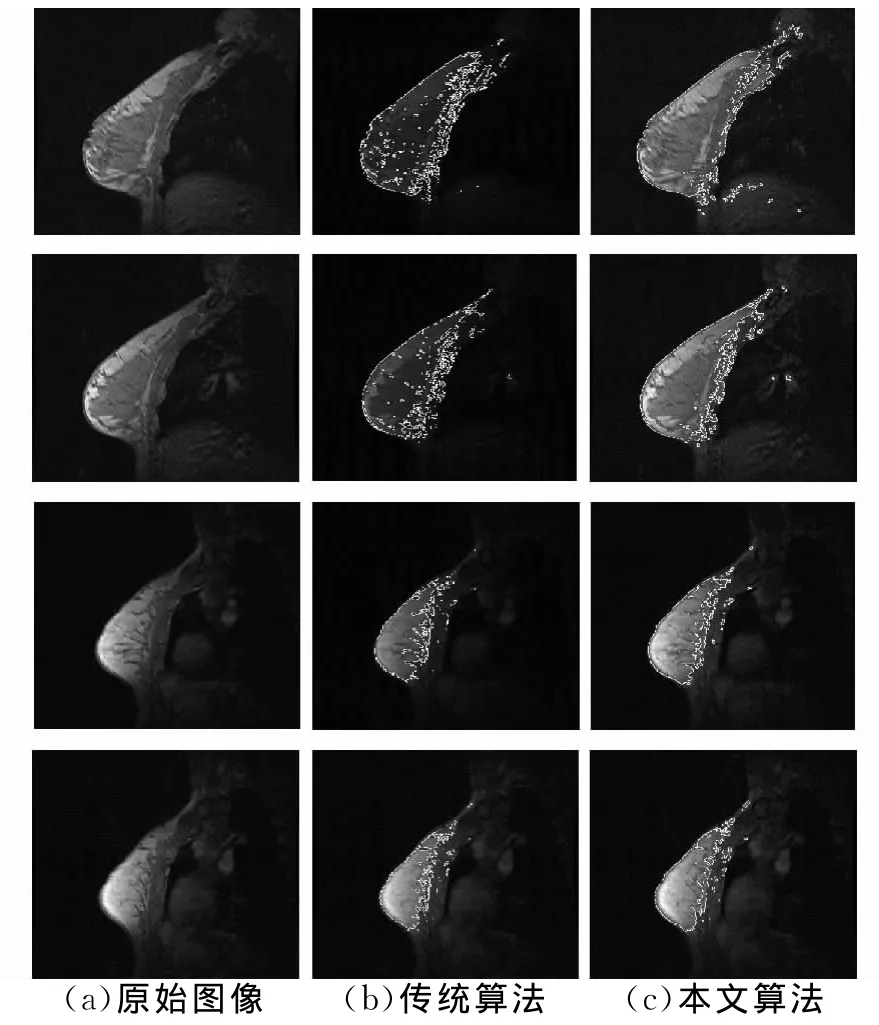
图3 矢状面乳腺MR图像A的分割对比图

图4 矢状面乳腺MR图像B的分割对比图

图5 冠状面乳腺MR图像的分割对比图
图6是用本文算法和传统算法对横断面成像图像的分割结果对比图,图像大小为256×256像素,灰度级为499。图中第1列是原始图像,第2列是加入均值和方差分别为0和0.01的高斯噪声后的图像(即含噪图像Ⅰ),第3列是加入均值和方差分别为0和0.1的高斯噪声后的图像(即含噪图像Ⅱ);第1行是分割前的图像,第2行是传统算法的分割结果(ν=499×499,迭代200次);第3行和第4行是本文算法的分割结果,其中第3行参数为h=2,ν=0,迭代5次;第4行调整空间尺度h为3,即参数为h=3,ν=0,迭代5次。

图6 横断面乳腺MR图像的分割对比图
根据实验结果可以看出,通过B样条基函数的连续水平集函数表示,大大降低了迭代次数,可通过灵活调整基函数的空间尺度参数h达到抑噪效果,且传统算法的局部极小值现象在本文算法中已经解决,即通过本文算法可以得到全局图像分割结果。由图3~图5可以看出,本文算法比传统算法获取的分割结果更为光滑且接近目标轮廓。比较图6第3行和第4行可以证明,本文利用B样条基函数表示水平集函数时,针对特定图像,可以通过适当调整空间尺度h的值得到最佳分割效果;比较第2行和第3行的最后一列分割图可以看出,本文算法对较高信噪比图像的分割效果明显好于传统算法的分割效果,即具有更好的抗噪性。
4 结 论
本文针对MR乳腺图像的分割难题进行了研究,提出一种基于改进CV模型的连续水平集算法,采用B样条基函数表示连续水平集函数,相比传统离散水平集函数大大降低了计算过程的复杂性,避免了水平集函数的重新初始化;基于改进CV模型的图像分割能量模型避免了分割陷入局部极小值现象,并且可有效抑制噪声。通过实验对仿真数据和临床数据进行了分割,结果表明:本文提出的基于改进CV模型的连续水平集算法可以准确、稳定地实现低信噪比、弱边界MR乳腺图像的分割,并具有一定的抗噪性能。
[1] KNOPP M V,GIESEl F L,MARCOS H,et al.Dynamic contrast-enhanced magnetic resonance imaging in oncology[J].Magn Reson Imaging,2001,12(4):301-308.
[2] OSHER S,SETHIAN J A.Fronts propagating with curvature dependent speed:algorithms based on Hamilton-Jacobi formulations[J].Journal of Computational Physics,1988,79(1):12-49.
[3] 龚永义,罗笑南,黄辉,等.基于单水平集的多目标轮廓提取 [J].计算机学报,2007,30(1):121-128.GONG Yongyi,LUO Xiaonan,HUANG Hui,et al.Multi-objects extracted based on single level set[J].Chinese Journal of Computers,2007,30(1):121-128.
[4] 王晓飞,庞全.基于圆形约束快速水平集的原生质体细胞分割 [J].中国图象图形学报,2013,18(1):55-61.WANG Xiaofei,PANG Quan.Protoplasm somatic cells segmentation based on circle dependent fast levelset segmentation[J].Journal of Image and Graphics,2013,18(1):55-61.
[5] 潘改,高立群,赵爽.基于局部熵的主动轮廓模型[J].中国图象图形学报,2013,18(1):78-85.PAN Gai,GAO Liqun,ZHAO Shuang.Active contour model driven by local entropy energy[J].Journal of Image and Graphics,2013,18(1):78-85.
[6] BALL J E,BRUCE L M.Level set-based core segmentation of mammographic masses facilitating three stage(core,periphery,spiculation)analysis[C]∥Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society,2007.Piscataway,NJ,USA:IEEE,2007:819-824.
[7] LIN Ning,YU Weichuan,DUNCAN J S.Combinative multi-scale level set framework for echocardiographic image segmentation[J].Medical Image Analysis,2003,7(4):529-537.
[8] 郭礼华,李建华,袁小彤,等.基于高斯矢量场的多尺度水平集图像分割算法 [J].上海交通大学学报,2005,39(8):129-133.GUO Li-hua,LI Jian-hua,YUAN Xiao-tong,et al.The multi-scale image segmentation algorithm based on Gaussian vector field(GVF)snake model[J].Journal of Shanghai Jicaotong University,2005,39(8):129-133.
[9] 余瑞星,李严俊,张科.基于小波变换的多尺度水平集算法研究 [J].光子学报,2007,36(2):372-375.YU Rui-xing,LI Yan-jun,ZHANG Ke.Multiresolution level set studying based on wavelet transform [J].Acta Photonica Sinica,2007,36(2):372-375.
[10]CHAN T,VESE L.Active contours without edges[J].IEEE Transactions on Image Processing,2001,10(2):266-277.
[11]OLIVIER B,DENIS F,PHILIPPE T,et al.Variational B-spline level-set:a linear filtering approach for fast deformable model evolution [J].IEEE Transactions on Image Processing,2009,18(6):1179-1191.
[12]MUMFORD D,SHAH J.Optimal approximations by piecewise smooth functions and associated variational problems[J].Communications on Pure and Applied Mathematics,1989,42(7):577-685.
