方括号多项式与双色多项式
2014-01-15韩友发张雪娇马野萍单亚男
韩友发,张雪娇,马野萍,单亚男
(辽宁师范大学 数学学院,辽宁 大连 116029)
0 引言
纽结多项式是纽结的重要不变量,在纽结的分类中扮演了重要角色.1928年,美国数学家Alexander[1]给出了纽结的一个多项式不变量.1969年,英国数学家Conway在研究Alexander多项式时,对其计算方法稍作改进,形成Conway[2]多项式.1984年,新西兰数学家Jones[3]从关于算子代数的定理中引申出纽结与链环的一个多项式不变量.然而Jones是一位泛函分析学家,他却在纽结理论中取得了重大突破,说明了表面上不同的数学分支之间有着深刻的联系和内在统一性.Kauffman在研究交错纽结的方括号多项式时,发现了方括号多项式与双色多项式之间存在着某种联系,这推动了纽结理论与图论之间的探索之路[4-5].
本文共分为三部分,第一部分简单介绍了纽结多项式;第二部分简单介绍本文所需的预备知识,包括纽结投影图的方括号多项式[K(G)]、平面图的双色多项式ZG(q,v)的定义,在交错纽结投影图与平面图之间建立一种联系,以及图论中的相关定义和性质;第三部分具体讨论ZG(q,v)与[K(G)]的性质以及它们之间的关系,同时研究了平面图的某些性质.
1 预备知识
纽结投影图的方括号多项式[K]是在不定向纽结上K定义的一个三元多项式,[K]∈Z[A,B,d],满足以下四个等式:
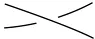



由上述公理,我们注意到方括号多项式[K]的计算是一种循环运算,因此我们给出[K]的另一种运算模式[6-8].
定义1.1当我们不考虑纽结投影图中上、下穿线时,将纽结投影图中每个交叉点变成相交点,得到的平面图形叫做四岔地图.如图1.1.

图1.1
因此,纽结投影图的方括号多项式的一般形式为[4]:
[K]=∑SAik(s)Bjk(s)d|s|
其中ik(s)+jk(s)=n为纽结图中交叉点的个数,S表示纽结投影图K的交叉点按照不同方式打开的所有状态,共有2n种打开方式.
定义1.2两个投影图称为等价的,或称为同痕的,如果从一个投影图出发,经过一连串的R1,R2,R3初等变换以及平面变形,可以得到另一个投影图.
定义1.3在纽结投影图中,如果沿着该图中的每条线,交叉点都是一上一下一上一下地相互交错出现的,则称该纽结为交错纽结.
定义1.4将交错纽结投影图K转化为四岔地图,四岔地图的各个区域标记为阴影部分或非阴影部分,满足以下两点:
(1)无边区域标记为非阴影部分;
(2)拥有一条公共边的相临两区域的颜色不同;
平面图Γ(Κ)中的顶点对应四岔地图中阴影部分,Γ(K)中的边对应四岔地图中的公共交叉点.
因此每个交错纽结投影图都对应一个平面图,若给出平面图G,满足定义1.1中的要求,可画出与其对偶的四岔地图,所以平面图与四岔地图是一一对应的关系.但是若给出一个四岔地图,我们无法唯一确定其对偶交错纽结投影图.因为每个四岔地图都对应两个交错纽结投影图,彼此互为镜面像.
引理1.1[6]互为镜面像的两个交错纽结投影图K与K′的方括号多项式[K]和[K′]满足下面等式:
[K](A,B)=[K′](B,A)
即将[K]中的变量A与B改为B与A,即可得到[K′].
对于平面图G,我们定义一个二元双色多项式ZG(q,v)∈Z[q,v],满足下面三个公理:

(2)Z·G=qZG
(3)Z·=q
当v=-1时,双色多项式特殊化为色多项式KG(q),既ZG(q,-1)=KG(q).由(3)可知,若平面图含有n个顶点,则色多项式KG(q)为关于q的一元n次多项式.KG(q)表示用q(≥2)种颜色对平面图G的顶点进行着色,使拥有公共边的相邻两顶点颜色不同,共有KG(q)种着色方法[9-10].
定义1.6一个平面G图定义为一个偶对(V,E),记作G=(V,E),其中
(1)V是一个集合,其中的元素称为顶点;
(2)E是无序积V×V中的一个子集合,其元素称为边;
集合V×V中的元素可在E中出现不止一次.在图论中,若连接同一对顶点的边数大于1,则称这样的边为多重边,其边数称为重数.
引理1.2平面图G含有多重边,平面图G′是将G中的多重边去掉,则两个平面图的色多项式均为KG(q).即多重边不影响平面图的顶点着色数目.
定义1.7平面图中不含圈的连通图称为树.
定义1.8如果在图G中删去一条边后,图G的分支数增加,则称此边为G的割边.
2 方括号多项式与双色多项式
引理2.1[4]令K(G)是与平面图G对偶的交错纽结投影图G,满足平面图的顶点对应K(G)的阴影部分(上穿线逆时针旋转扫过的区域),则由K(G)的方括号多项式可导出G的双色多项式:

上述引理仅限于部分交错纽结,具有一定的局限性.但我们知道另外一部分交错纽结与此部分交错纽结互为镜面像.由引理2.1可知两者的方括号多项式之间存在着必然的转换关系.因此本文涉及到的交错纽结均可以与平面图建立一一对应关系.
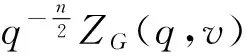

q=d2
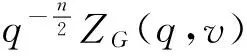
与方括号多项式[K(G)]比较,每一单项式中缺少变量B.由方括号多项式的计算公理可知,[K]的一般形式为:
[K]=∑SAik(s)Bjk(s)d|s|
其中ik(s)+jk(s)=n为纽结投影图中交叉点的个数.如果知道每一单项式中变量A或B的指数,即可求出另一变量的指数.
因此,在多项式f(A,d)中,每一项添加变量B,使得A、B的指数和为纽结投影图中交点总数.
这样,我们由G的双色多项式ZG(q,v)导出了K(G)的方括号多项式[K(G)].证毕.
引理2.2[10]如果图G是子图H和K的并,且H∩K当且仅当是一个顶点,那么
通过方括号多项式的计算公理仍能得到上述结果,但是计算相对繁琐些.我们注意到,利用平面图的双色多项式计算其对偶交错纽结投影图的方括号多项式更便捷一些,这也是研究两者关系的重要意义之一.为此我们有必要详细研究一下有关平面图的双色多项式计算的相关性质.
引理2.3[11]树的双色多项式的一般形式为:
ZG(q,v)=q(a+v)n
其中n表示树的树枝数,与树枝的排列方式无关.
定理2.2(1)简单n边形的双色多项式的一般形式为:
(2)平面图G是在简单n边形的基础上,仅多添加一条重边,则其双色多项式的计算满足如下关系:
ZG(q,v)=ZG′(q,v)+v(v+1)ZG″(q,v)
其中G′表示G去掉重边后的n边形,G″表示比G′少一条边的n-1边形,当n=1时,G″表示一个点.
该定理利用归纳法以及引理2.2、引理2.3可以证明.同时该结果说明了重边对于平面图的顶点着色问题无实质影响.
推论2.1平面图G是在简单n边形的基础上含有一条重边,则其双色多项式的一般形式为:
ZG(q,v)=(v+2)
推论2.2平面图G是在简单n边形的基础上,在其一边上具有m重边,则其双色多项式的计算公式满足:
其中G′表示G去掉m重边后的n边形,G″表示比G′少一条边的n-1边形.
定理2.3如果平面图G是子图H和K的并,
且H∩K只是一条边,那么
其中G-1表示平面图G去掉公共边后的图形,H-1表示H收缩公共边后的图形,K-1表示K收缩该公共边后的图形.
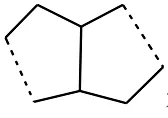
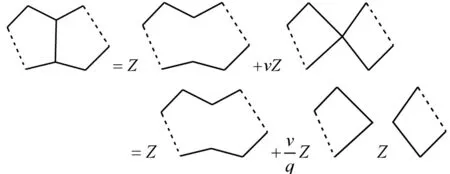
因此,
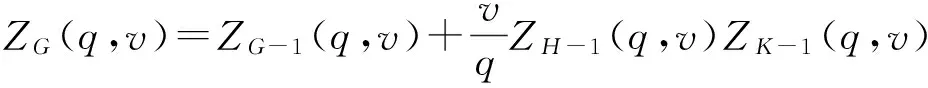
引理2.4[11]如果图G是子图H和K的不交并,那么
ZG(q,v)=ZH(q,v)ZK(q,v).
根据本引理以及双色多项式的性质可以证明下面的结果.
定理2.5如果平面图G是子图H和K当且仅当通过一条边连接,该边为图G的割边,那么
以上是有关平面图双色多项式的计算的相关性质,利用这些性质可以给出双色多项式的简化计算,进而简化对偶交错纽结投影图的方括号多项式的计算过程.从而可以研究与平面图着色的相关问题[12].
[1]J.W.Alexander.Topological invariants of knots and links[J].Trans.Amer.Math.Soc.,1923,30:275~306.
[2]J.H.Conway.An enumeration of knots and links and some of their algebraic properties[J].Computational Problems in Abstract Algebra,Pergamon Press,New York,1970,329~358.
[3]V.F.R.Jones.A new knot polynomial and von Neumann Algebras[J].Notices of AMS,1985.
[4]L.H.Kauffman.New Invariants in the Theory of Knots[J].The American Mathematical Monthly,1988,95(3):195~242.
[5]Xian’an Jin,Fuji Zhang.The Homfly and dichromatic polynomials[J].Proc.Amer.Math.Soc..2012,140(4):1459~1472.
[6]Rolfsen.Dale.Knots and links[M].Publish or Perish,1976.
[7]Han,Youfa;Li,Yang.The bracket polynomial of links[J].Liaoning Norm.Univ.Nat.Sci..2000,23(1)
[8]Itik Mehmet,Banks Stephen P.On the calculation of the Kauffman bracket polynomial[J].Applied Mathematics and Computation,2010,216(2):655~661.
[10]W.T.Tutte.Graph Theory[M].Addison-Wesley,Reading,MA,1969.
[11]B.Bolloba.Modern Graph theory[M].Springer,Berlin,1998.
[12]Han,Youfa;Zhang Da-wei,SUN Sheng.Jones Polynomial of Knots and Laurent Polynomial[J].Jilin Norm.Univ Nat.Sei,2012,33(4):19~31.
