一类奇异偏微分方程的化简方法
2014-01-15李平丽孙甜甜
李平丽,孙甜甜
(1.渤海大学 数理学院,辽宁 锦州 121013;2.渤海大学 数理学院,辽宁 锦州 121013)
0 引言
偏微分方程(组)的化简问题在微分方程的分类研究与研究解的性质及求解方法等问题[3-7]中占有不可或缺的地位,不同类型的方程(组),其化简及求解方法也不尽相同,例如,李群方法中(见[8-11]),有一类偏微分方程(组)可通过坐标变换使方程(组)不显含某个变元,进而,在某些特殊情况下,求出方程(组)的一些特解.再例如,文献[5]通过引入广义状态向量及其伴随向量,解耦振动方程,进而将二阶微分方程化为一组一阶可解微分方程研究其解.
定理A[1][2]考虑微分方程
其中R2(x,y)为关于两个复变量x与y的幂级数,在C2的原点附近收敛,且只含2阶及高阶项.如果α∉N-{0},那么该方程存在唯一满足条件φ(0)=0的全纯解y=φ(x).
1 主要结论
考虑1阶偏微分方程

(1)
其中,a(x,y),b(x,y),c(x,y)在原点0∈C2附近解析,且a(x,y),b(x,y)在0∈C2处的幂级数展开式中不含常数项与线性项.5元复变量函数G(z1,z2,z3,z4,z5)在原点附近解析,且满足

定理存在双全纯变换,使偏微分方程(1)化为如下形式

(2)
其中,二元复变量函数g(u,v),c1(u,v)均在原点附近解析,且g(0,0)=0,5元复变量函数G1(z1,z2,z3,z4,z5)在原点附近解析,并且满足

2 结论的证明
作变量变换

其中,h(v)待求,满足条件:h(v)为原点附近的解析函数,且h(0)=0.则
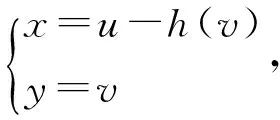
因而,偏微分算子

化为


记F(u,v)=-h(v)-vh′(v)+a(u-h(v),v)+b(u-h(v),v)h′(v).
断言:若令h(v)+vu(v),则存在原点附近的单复变量解析函数u=u(v),使u(0)=0,且F(0,v)=0,即:
-h(v)-vh′(v)+a(-h(v),v)+b(-h(v),v)h′(v)=0.
事实上,将h(v)=vu(v)代入上式得
a(-uv,v)+b(-uv,v)(u+vu′)-2uv-v2u′=0,
再由a(x,y)与b(x,y)的性质,可得
v2a1(u,v)+v2b1(u,v)(u+vu′)-2uv-v2u′=0,
此处,2元复变量函数a1(u,v)与b1(u,v)均为原点附近的解析函数.于是有
va1(u,v)+vb1(u,v)(u+vu′)-2u-vu′=0,
即
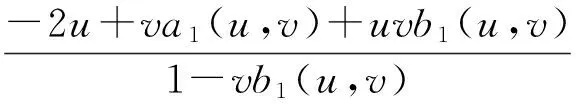
进而,只需u满足常微分方程
vu′+2u=vc1(u,v).
(3)
其中,2元复变量函数c1(u,v)在原点附近解析.
由定理A可知,常微分方程(3)存在唯一在原点附近解析的解u=u(v)满足初始条件u=u(0).因此,断言成立.
因此存在一个在复平面中原点附近解析的函数h(v),且满足条件h(0)=0,使得以下变量变换

将奇异偏微分算子

化为如下形式

其中
uf(u,v)=a(u-h(v),v)-a(-h(v),v)
+[b(u-h(v),v)-b(-h(v),v)]h′(v),
且f(u,v)在0∈C2附近解析,f(0,0)=0.因此

再由函数b的性质得


变换后的偏微分方程两端同时除以1+f(u,v),即可得方程(2).结论得证.
3 结束语
以上处理偏微分方程的化简这一问题的方法,给此类问题提供了又一思路:在构造变量变换时,不必将变换以具体表达式的形式写出来,只需证明具有满足条件的函数使得变换存在即可.
[1]R.Gerard,H.Tahara.Singular Nonlinear Partial Differential Equations[M].Wiesbaden,1996.
[2]Ch.Briot,J.CI.Bouquet.Recherches sur les proprietes des fonctions definies par des equations differentielles[J].J.Ecole Polytech.21 (1856),133~197.
[3]L.C.Evance.Partial Differential Equations[M].American Mathematical Society.1998.
[4]谷超豪,李大潜,陈恕行,郑宋穆等.数学物理方程[M].第三版.高等教育出版社.2012.
[5] 张淼.亏损结构振动方程的稳态响应求解[J].吉林师范大学学报(自然科学版),2014,35(1):91~94.
[6] 郭时光.关于二阶偏微分线性方程的化简[J].科协论坛(下半月).2010,5:72~73.
[7] 刘 胜,管克英.偏微分方程组的一种化简方法[J].北京航空航天大学学报.1999,25(1):100~103.
[8] K.Tenenblat, P.Winternitz.On the symmetry groups of the intrinsic generalized wave and Sine-Gordon equations[J].J.Math. Phys., 1993,34(8):3527~3542.
[9] P.G.L.Leach, S.Bouquet, A.Dewisme. Symmetries of Hamiltonian one-dimensional systems. Int. J. Non-Linear Mechanics,1993,28(6):705~712.
[10]A.H.Kara,F.M.Mahomed. A note on the solutions of the Emden-Fowler equation[J]. Int.J.Non-Linear Mechanics,1993,28(4):379~384.
[11] M.S.Velan, M.Lakshmanan. Lie symmetries and invariant solutions of the shallow water equation[J]. Int. J. Non-Linear Mechanics,1996,31(3):339~344.
