混合截尾试验下双参数韦布尔分布可靠性指标的参数估计
2014-01-15孙晓祥印赞华冯毅夫李玉玲杜宇静
孙晓祥,印赞华,冯毅夫,李玉玲,杜宇静
(1.吉林农业科技学院 文理学院,吉林 吉林 132101;2.赣南师范学院 数学与计箅机科学学院, 江西 赣洲 341000;3.吉林师范大学 数学学院,吉林 四平 136000;4.北京师范大学珠海分校 应用数学学院,广东 珠海519085)
0 引言
在可靠性试验中,我们通常研究定数截尾和定时截尾两种情况.定数截尾寿命试 验是指试验到指定的失效个数停止.定时截尾寿命试验是指试验到指定时间就立即停 止实验.定数截尾和定时截尾结合在一起的试验是混合截尾试验,文献[1-2]最先研究 了混合截尾试验.近些年,混合截尾试验在可靠性和寿命试验中应用越来越广泛,国 内外很多专家学者对此问题都进行了深入的研究,例如,文献[3]研究了指数分布的混合删失计划,文献[4]研究了混合截尾试验下指数分布的统计推断.在国内,文献[5] 研究了混合截尾寿命试验情形下指数分布平均寿命的置信限,文献[6]研究了多次混合截尾寿命试验指数分布平均寿命的的统计推断,文献[7]研究了指数分布下混合截尾 试验参数二次极大似然估计,文献[8]研究了 II型截尾情形下泊松分布参数的估计.
在可靠性试验中,韦布尔分布是可靠性中常用的失效分布之一,许多电子机械的 元件与设备等产品的失效时间分布都是韦布尔分布.因此研究混合截尾试验下韦布尔 分布的参数估计是非常有意义的.很多情况下,在可靠性研究中,我们关心的不仅是 模型的参数,而且关心可靠性指标,如可靠度函数和可靠寿命等,它们都是参数的函 数.因此本文我们研究混合截尾试验下双参数韦布尔分布的参数估计和可靠性指标的 参数估计及估计量的性质.第一部分研究了混合截尾试验下双参数的韦布尔分布的参 数估计,并研究了估计量的性质,第二部分研究了可靠性指标如可靠性函数和可靠寿 命的估计,第三部分研究了区间估计,第四部分进行了模型研究,第五部分对所给出 的理论用实例进行具体的分析.
1 韦布尔分布参数的极大似然估计及其估计量的渐近性质
混合截尾试验是指从总体中随机抽取n个样本,对它们同时进行寿命试验,事先 定下至多允许失效数r(r≤n)和试验的至多进行时刻,如果在时刻t0之前观测到r个失效,则试验就在第r个失效的时刻tr停止,否则就进行到时刻t0终止.
下面我们研究混合截尾试验下双参数的韦布尔分布的参数估计.

当tγ 为了简便,设 则混合截尾试验下的似然函数 (1.1) 其对数似然函数为 (1.2) 分别关于参数m和β求一阶导数并令一阶导数为零得 通过解似然方程可得参数m和β的最大似然估计. 很多情况下,在可靠性研究中,我们关心的不仅是模型的参数,而且关心这些参 数的函数.例如,工程师更关心系统的可靠度函数和可靠寿命,他们都是模型参数的函数.下面我们给出可靠度函数和可靠寿命的极大似然估计. 韦布尔分布下可靠度函数. 在DSP中实现H.264的编码器优化,优化过程主要为4步:算法优化、C代码优化、线性汇编的优化和CCS编译器选项优化[11]。优化过程如图7所示。 对韦布尔分布的参数的最大似然估计,根据极大似然估计的不变性,则得韦布尔分布 混合截尾试验下可靠度函数的极大似然估计为 定义设产品的可靠度函数为R(t),使其等于给定值R(0 考虑检验问题:H0:m=m0,H1:m≠m0.似然比统计量为 本节中我们随机模拟了t=0.25时(n,r)分别为(15,5),(25,5),(50,10),(50,15)情况下参数m和的最大似然估计.表1中第二列第三列给出了参数m和β的最大似然估计量的偏差,第四列为可靠度函数的最大似然估计的偏差,第五列为可靠寿命的最大似然估计的偏差,括号中为相应的均方误差.本模拟重复计算50次. 表1 参数和参数的函数的最大似然估计的偏差和均方误差 从表1的结果来看,当n固定r增加或者r固定n增加时估计量的偏差和均方误差都减少. 例36个家电前10个家电的失效时间为:11,35,49,170,329,381,708,958,1062,1167,t0=2600.计算参数的极大似然估计及可靠性函数和可靠 寿命的估计值和并给出相应的置信区间. 解:本例中r=10,n=36,tr=116,t0=2600,D=r=10. 当α=0.5时,参数m的渐近置信区间为[1.38,2.21],β的渐近置信区间为[7.558×105,10.856×105]. 参数m的基于似然比的置信区间为[1.69,2.85],β的基于似然比的置信区间为 [7.808×105,11.235×105]. [1]Epstein,B.Truncated life-tests in the exponential case[J].Ann.Math,Statist,1954,25:555~564. [2]Epstein,B.Estimation from llife-test data.Technometric[J].1960,2:447~454. [3]Gupta,R.D.and Kundu,D.Hybrid censoring schemes with expinential failure distribution[J].Comm,Statist.-Theory Methods 27:3065~3083. [4]Childs,A.Chandrasekhar,B.,B alakrishshnan N.,and Kundu,D.Excat likelihood inference based on Type- I and Type- II hybrid censored samples from the exponential distribution[J].Ann.Inst.Statist.Math.2003,55:319~329. [5]王 宏.混合截尾寿命试验情形下指数分布平均寿命的置信限[J].应用概率统计,1996,12(4):33~36. [6]李 林.多次混合截尾寿命试验指数分布平均寿命的统计推断[D].北京大学硕士学位论文,2005 [7]冯文雅,刘瑞元.指数分布下混合截尾步加试验参数二次极大似然估计[J],甘肃联合大学学报 (自然科学版),2009,23(4):14~17. [8]刘银萍,宋立新.II型截尾情形下泊松分布参数的估计[J].吉林大学学报(理学版),2007,45(6):941~945. [9]刘银萍,构晓莹,赵志文.截断情形下巴斯卡分布的参数估计[J].吉林师范大学学报(自然科学版),2009,2(3):4~6. [10]刘银萍,安丽微.缺失数据情形下两个Poisson分布总体参数的估计和检验[J].吉林师范大学学报(自然科学版),2011(3):2:11~13. [11]王玉芳.定数截尾数据缺失场合下k(m)/n系统可靠性指标的经验Bayes估计[J].吉林师范大学学报(自然科学版),2012,4(33):41~43.



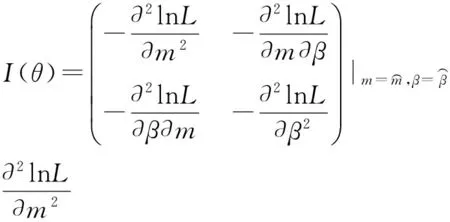
2 可靠度函数和可靠寿命的极大似然估计


3 区间估计
3.1 渐近置信区间
3.2 基于似然比的置信区间

4 模拟研究

5 实例分析

