基于B样条自由形变三维医学图像非刚性配准研究

冯兆美，党 军，崔崤峣，焦 阳

（1．中国科学院 苏州生物医学工程技术研究所，江苏 苏州215163；2．中国科学院 长春光学精密机械与物理研究所，吉林 长春130000；3．中国科学院大学，北京100049）

医学图像配准是指采用适当的空间变换方法，使一幅医学图像与另一幅医学图像上对应的解剖结构点、具有诊断意义的点以及手术感兴趣的区域达到空间位置上的一致［1］。多模态医学图像配准在医学诊断和治疗计划中有着重要作用。但由于成像方法以及病人器官解剖特征结构的不同，使得准确、高效的对多模态医学图像进行非刚性配准成为一个难题［2］。

例如超声成像（Ultrasound，US）因具有实时成像、低成本和无辐射等优点在临床领域被广泛应用，特别是用于引导介入和术中监测等方面。CT图像由于其根据人体各种组织或器官对X射线吸收不等的特性进行扫描，所以对人体各个器官呈现断层切面且图像分辨率较高，但CT成像更适合进行手术前的诊断。由于超声图像能够实时快速的提供诊断数据，CT图像能够保证数据的准确详细，所以进行超声图像和CT图像的配准研究在临床诊断效率、实时病情监测、提高外科手术水平等方面具有重要的临床应用价值。近些年，三维图像非刚性配准算法逐渐成为专家学者研究的重心，Wein Wolfgang［3］等人采用刚性与放射变换模型，对超声图像与CT进行自动化配准，并对此方法进行评估；卢振态［4］等人提出一种新的基于主成分分析的三维医学图像快速配准算法，此方法能够显著减少计算量，并且不需要复杂的优化过程；Rueckert Daniel［5］等人提出利用自由形式变换模型对三维乳腺MRI图像进行非刚性配准；Roche Alexis和Pennec Xavier［6］等提出将基于图像梯度与灰度的混合配准模型应用于乳腺MRI图像的非刚性配准中。不断有基于新的数学模型的算法出现，如 Tanner Christine［7］等人建立了错切变换与椭球压缩模型描述乳腺形变；Mark Holden［8］使用微分同胚时空映射来正则化速度场，避免求解Navier－Stokes方程时遇到的奇异点问题。

本文采用加入薄板样条能量约束项的互信息［9］作为相似性测度对3－D超声图像和3－D CT图像进行配准，联合刚性变换和自由形变模型，并使用有限内存的拟牛顿优化方法（L－BFGS－B）［10］对变形参数进行优化搜索。采用基于体素的方法计算相似度时，对于较高分辨率的三维体数据集，其包含的数据量极大，为减少计算量，计算前先对原图像进行重采样。同时在非刚性配准之前，首先对两幅图像进行刚性配准，以使得在非刚性配准前两幅图像的初始几何偏差达到最小。在配准过程中，采用多分辨率和多重网格的策略，以提高配准过程的速度和精度，避免局部极值问题的产生。最后使用互信息值、相对重叠率和运行时间对乳腺仿体的超声数据和CT数据配准的精度和速度进行评价。此外，还使用了29组人体肝脏超声数据和3组人体胸腔CT图像进一步验证算法性能。

1 原理与方法

假设参考图像（Reference Image）为fR（X），另一幅待配准的测试图像（Testing Image）为fT（X），使用g（X｜μ）描述图像形变，μ是一系列的变换参数。将医学图像配准看成是一种优化问题，那么校准参考图像和变换后的测试图像的主要任务就是寻找一组最优的变换参数μ使两幅图像差异S最小，数学表示如下：

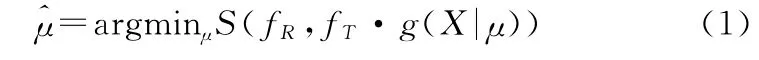
1．1 变形模型的建立

基于样条函数的配准方法主要利用控制点和样条函数来描述非线性几何变换域。将位于样条函数栅格上的控制点赋值，当这些控制点产生空间位移时，样条函数被弯曲，那么控制点周围的图像空间也会随着样条函数的弯曲而产生不同程度的扭曲。本文使用基于B样条的自由形变模型（free form deformation，FFD）［11］。在三维空间域中，基于B样条函数的自由形变可描述为三个一维三次B样条函数的张量积：

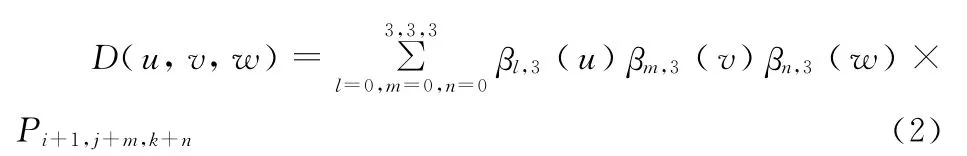
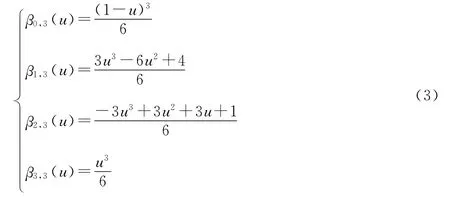
其中βi（u）为第i次B样条的基函数：

同时用一个旋转矩阵R和一个3元素的平移向量T建立刚性的全局变形模型，这样应用于测试图像的非线性变换为：

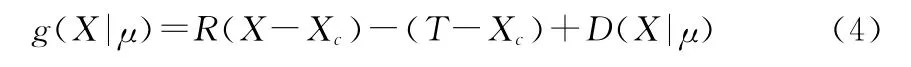
其中Xc是测试图像体素的中心坐标。

基于B样条的自由形变模型是非刚性配准的重要手段，它能够有效地拟合物体的弹性形变。FFD变换的自由度很高，可以实现局部控制并且变换域C2连续性［11］，能够确保在优化过程中使用基于梯度有约束优化方法。但是此变形可能产生不可逆的空间变换函数，即当某些B样条网格中的节点位移过大时，会导致图像折叠［12］。为了得到一个可逆的空间变换函数以避免折叠现象发生，需要对节点的位移大小进行约束。根据3次B样条的可逆性条件［7］，第（i，j，k）个控制点的位移dx、dy、dz应满足条件dx＜sx／k、dy＜sy／k、dz＜sz／k，k是常数，在三维空间变换的情况下取值为2．47947。由于限制了节点位移的大小，一层固定网格间距的B样条模型就不能完成大规模形变，需要引入多层次B样条模型［13］。多层次B样条模型采用多个由疏到密的网格，分层依次对图像进行配准。

1．2 互信息相似性测度

互信息［14］是一种基于熵的方法，广泛应用于多种不同模式图像的配准，互信息方法同时也是配准精度和鲁棒性最好的可回溯性配准方法之一。假设两幅图像分别用两个随机变量A，B表示，其边缘概率分布为pA（a）与pB（b），联合概率分布为pAB（a，b）。那么用互信息来衡量图像之间的相似程度，其数学表达式为

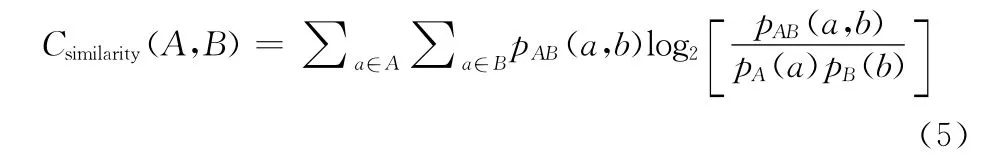
非刚性配准中，变换模型内部完全保证几何变换的平滑可逆是一个病态问题，配准过程中会出现一定程度的图像交叉和重叠问题。本文通过在配准代价函数中加入一个几何变换的约束项解决此问题，即在目标函数中加入薄板样条能量约束项［17］。

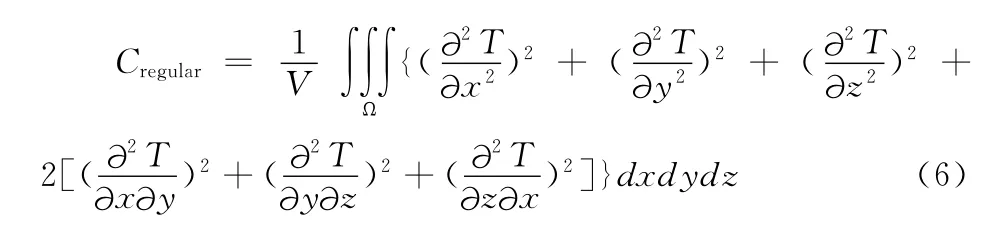
那么配准的代价函数为：

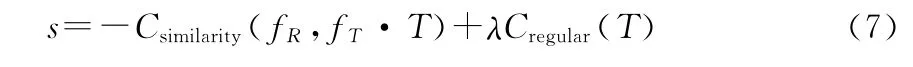
其中，λ为常量权重因子，其为经验值。在λ＝0．01时，使得目标函数中相互竞争的两部分能够很好的折衷。通过实验发现，当控制点网格分辨率较低时，λ对B样条的平滑性影响不大，但是随着控制点网格分辨率的提高，约束项的作用愈加明显。原因是FFD对图像局部的变形能力随着控制点网格间距的减少而增强。因此，在致密控制点网格中尤其需要约束项。

1．3 多分辨率优化策略

本文采用L－BFGS－B优化方法，基于B样条的自由形变模型的互信息配准算法运算量比较大，而L－BFGS－B［15］优化方法能够解决求解过程占用大量内存而降低运算速度的问题。多分辨率优化策略［16］亦是一种有效提高算法的执行速度和避免陷入局部极值的方法。因此可以采用多分辨率的分级配准策略，配准按照由粗到精的方式执行。配准将分为两个层次进行，第一层只包含刚性变换参数的粗配准，第二层只包含自由形变参数的精细配准。将刚性变换得到的参数作为第二层精细配准的初始值。配准框架如图1。图中被细线框住的部分是算法的核心，包括对目标函数的计算和优化，L－BFGS－B为寻找空间变换参数μ的优化器。当同时满足终止1的条件（目标函数值与目标函数的梯度值满足预设的阈值，默认值分别为1e－3，1e－4）与终止2的条件（迭代次数，默认值为500），输出配准图像、运行时间以及变形参数。

2 实验结果与分析

为了检验本文算法对三维超声图像与CT图像配准的效果，使用乳腺仿体的超声图像和CT图像进行非刚性配准实验。此外，使用29组人体超声图像对和3组人体胸腔CT图像对进一步验证算法性能（硬件环境为Intel（R）Core（TM）i3－2 1 2 0CPU＠3．3 0GHz和4．0 0GB RAM ；软 件环境为 Microsoft VS2008，ITK 3．20，VolView 3．4，Matlab R2011b，Windows 7）。

图1 多分辨率图像配准框架

图2 乳腺仿体的超声－CT图像

本文使用的是一种乳腺超声活检训练用仿体（052A 模型，CIRS，Tissue Simulation ＆ Phantom Technology，USA）采集超声与CT数据。在使用ATL HDI 5000Ultrasound系统扫描超声数据过程中，将乳腺仿体浸入在水槽中，使用二维线阵探头进行垂直无接触式扫描，扫描步长为2 mm／帧，将获得的二维超声数据重建成三维体数据（图2b）。在Philips Gemini TF 64PET／CT系统上收集CT图像（图2a）。将采集到的超声图像与CT图像进行配准，图2是乳腺仿体的超声体数据与CT体数据，其中CT图像的大小为240×145×425，像素间距0．35×0．35×0．33；超声图像的大小为482×308×30，像素间距为0．35×0．35×0．33。图中箭头标识的部分是“肿瘤”部分。图3是其配准结果，图像的大小为482×308×30，像素间距为0．35×0．35×0．33。我们给出其三维体积图与横断面、冠状面、矢状面三个方向上的信息。从图3可以看出，与原始的超声图像相比，配准后的图像更加光滑，但是肿块边缘仍然有一定程度上的模糊，这是因为：1）超声图像有噪声；2）与CT体积图425个切片相比，超声体积图只有30个切片，使得超声图像横截面的分辨率更低，失去更多的结构信息。

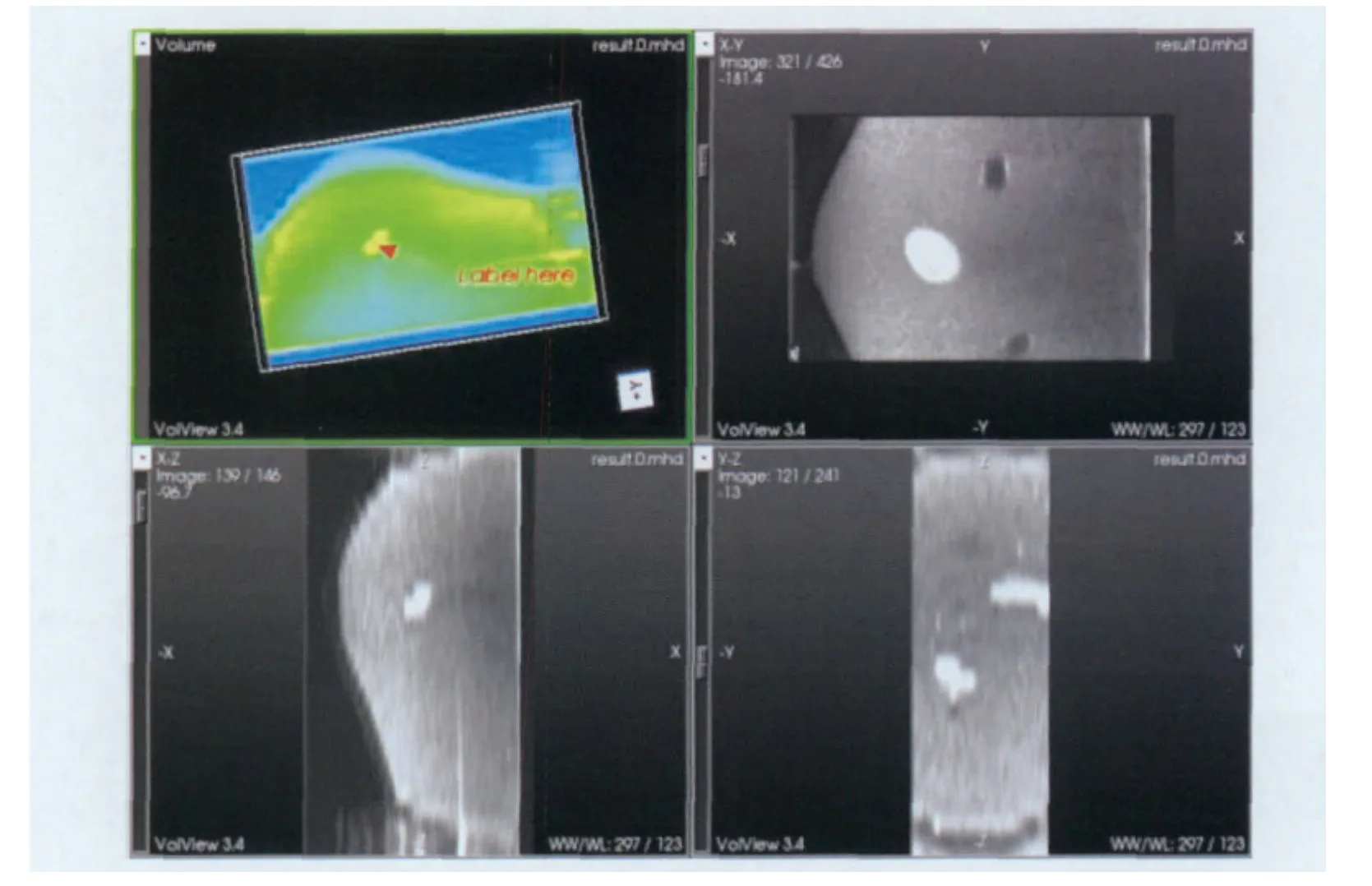
图3 US－CT配准结果

收集29组合适的人体肝脏超声图像数据，在ATL HDI 5000Ultrasound系统上，使用扇形扫描方式得到超声体数据。超声图像的分辨率为512×512×256，像素间距为0．427×0．387×0．823。图4是同一病人不同时间扫描的肝脏超声图像，图4a为参考图像，图4b为测试图像，其中箭头标志为目标区域。图5为两幅超声图像的配准结果，图像的大小为512×512×256，像素间距为0．427×0．387×0．823。我们给出其三维体积图与横断面、冠状面、矢状面三个方向上的信息。从图中可以看到，箭头标志部分整体上对齐较好。

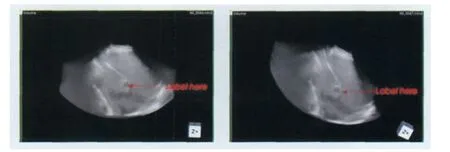
图4 肝部超声临床图像

图5 肝脏超声图像配准结果

在Philips Gemini TF 64PET／CT 系统上收集到3组合适的人体胸腔CT图像，CT图像的分辨率为512×512×41，像素间距为0．703×0．703×0．817。图6是同一病人不同时间扫描的胸腔CT图像，其中图6a为参考图像，图6b为测试图像图。图7为其配准结果，图像的大小为512×512×41，像素间距为0．703×0．703×0．817。我们给出其三维体积图与横断面、冠状面、矢状面三个方向上的信息。

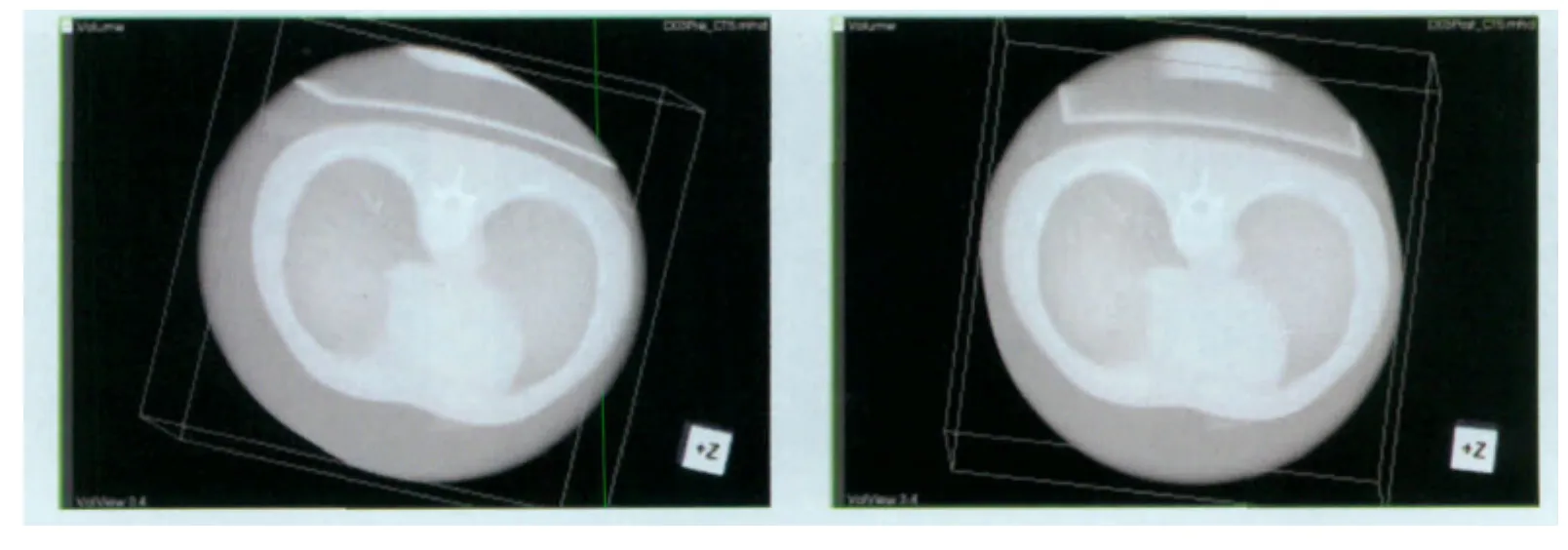
图6 胸腔CT图像

3 方法评价

图像配准是为某一特定目的而在某种特定原则下寻求相对最优结果，针对非刚性多模态图像配准，由于获取图像的本质上有很大程度的不同，使得像素点之间的对应关系是未知的，所以很难

对这些算法进行评估，无法指定一个统一的金标准对任意配准结果进行客观判定，但是可以使用多种不同标准提供的信息来评估非刚性配准算法的性能［17，18］。

感兴趣区域的对齐程度［18］能够很好的体现出两幅图像的配准效果，即两个对应的分割区域的重叠率。相对重叠率数学表达如式8，其中P与S是相对应的分割区域。

我们请五位有经验的专家分别从体积图中手动分割出目标区域。图8给出配准前后图像对应目标区域的重叠图像，用白色表示配准前的目标区域，彩色表示配准后的目标区域。其中，图8a是乳腺仿体中的肿块区域重叠图，图8b是超声图像目标区域的重叠图像，图8c是从CT胸腔图像分割出的肝脏重叠图。配准前后的目标区域整体上能够达到空间位置上的对齐。

图7 胸腔CT图像配准结果

图8 目标区域的重叠图

在本次配准实验中，将本算法与互信息配准算法［11］、Demons配准算法［19］进行比较，从互信息值、相对重叠率指标、程序运行时间等方面评价算法精度与效率。配准结果评价见表1，表中 MIp为带有约束项的互信息相似性函数，MI配准前后两图像的互信息值，ROI为感兴趣区域的相对重叠率，Time为程序的运行时间。

从表1中可以看出，使用本算法对乳腺仿体的超声数据与CT数据进行配准得到了较好的实验结果：未改进算法的感兴趣区域的相对重叠率为89．03%，带有薄板样条约束项的B样条自由形变非刚性配准算法得到的感兴趣区域的相对重叠率最高为91．28%，精度提高2．5%；Demons方法运行时间为1137s，本算法运行时间55s，运行时间提高了19．7倍。此外，用29组超声图像、3组CT图像验证本算法对临床数据配准的可行性，得到的实验结果为：在非刚性配准中具有薄板样条约束项的配准方法得到的感兴趣区域重叠率为89．87%，无约束项的配准方法其感兴趣区域的相对重叠率为91．38%，精度提高1．7%左右；本算法的平均运行时间为266s，Demons方法运行时间为2276s，运行效率提高了7．6倍。

表1 配准结果评价The evaluations of the image registration results

4 结论

本文将基于互信息的非刚性配准方法应用在超声图像和CT图像配准中，并在互信息中加入薄板样条能量约束项，以避免配准过程中图像交叉与重叠问题的出现。联合刚性变换和B样条自由形变的非线性变换方法，使用L－BFGS的优化方法对变换模型中的参数进行多分辨率优化搜索。在此基础上，使用感兴趣区域的相对重叠率、互信息值、配准运行时间对本算法进行评价，与没有约束项的互信息方法以及微分同胚的Demons配准方法比较。得到如下结论：未改进算法得到的感兴趣区域重叠率为89．58%，而带有薄板样条约束项的改进算法得到的感兴趣区域重叠率为91．35%，精度提高2．0%。Demons方法平均耗时1896s，本文改进算法平均耗时195s，运行效率提高8．7倍。实验结果表明此算法能够对超声和CT图像进行配准并获得较好的结果。

［1］ Brown L G．A survey of image registration techniques［J］．ACM Computing Surveys（CSUR），1992，24（4）：325－376．

［2］ 田 捷，戴晓倩，杨 飞．医学成像与医学图像处理教程［M］．北京：清华大学出版社，2013．152－229．Tian J，Dai X Q，Yang F．Medical Imaging and Medical Images Processing ［M］．Beijing：Tsinghua University Press，2013．187－189．

［3］ Wein W，Brunke S，Khamene A，et al．Automatic ct－ultrasound registration for diagnostic imaging and image－guided intervention［J］．Medical Image Analysis，2008，12（5）：577－585．

［4］ 卢振泰，陈武凡．基于主成分分析的三维医学图像快速配准算法［J］．南方医科大学学报，2008，28（9）：1591－1593．Lu Z T，Chen W F．A fast 3－d medical image registration algorithm using principal component analysis ［J］．Journal of Southern Medical University，2008，28（9）：1591－1593．

［5］ Rueckert D，Sonoda L I，Hayes C，et al．Nonrigid registration using free－form deformations：application to breast MR images ［J］．IEEE Transactions on Medical Imaging，1999，18（8）：712－721．

［6］ Roche A，Pennec X，Malandain G，et al．Rigid registration of 3－d ultrasound with MR images：a new approach combining intensity and gradient information［J］．IEEE Transactions on Medical Imaging，2001，20（10）：1038－1049．

［7］ Tanner C，Karssemeijer N，Székely G．Deformation models for registering MR and 3dultrasound breast images ［C］．IEEE International Symposium on Biomedical Imaging：From Nano to Macro，2011．582－585．

［8］ Holden M．A review of geometric transformations for nonrigid body registration［J］．IEEE Transactions on Medical Imaging，2008，27（1）：111－128．

［9］ Pluim J P W，Maintz J B A，Viergever M A．Mutual－information－based registration of medical images：a survey ［J］．IEEE Transactions on Medical Imaging，2003，22（8）：986－1004．

［10］ Zou X L，Navon M，Berger M，et al．Numerical experience with limited－memory quasi－newton and truncated newton methods［J］．SIAM Journal on Optimization，1993，3（3）：582－608．

［11］ Mattes D，Haynor D R，Vesselle H，et al．Pet－ct image registration in the chest using free－form deformations［J］．IEEE Transactions on Medical Imaging，2003，22（1）：120－128．

［12］ Rueckert D，Aljabar P，Heckemann R A，et al．Diffeomorphic registration using b－splines［C］．Medical Image Computing and Computer－assisted Intervention Miccai 2006．2006，Springer．p．702－709．

［13］ Xie Z Y，Farin G E．Image registration using hierarchical b－splines［J］．IEEE Transactions on Visualization and Computer Graphics，2004，10（1）：85－94．

［14］ Maes F，Collignon A，Vandermeulen D，et al．Multimodality image registration by maximization of mutual information ［J］．IEEE Transactions on Medical Imaging，1997，16（2）：187－198．

［15］ Nocedal J．Updating quasi－newton matrices with limited storage ［J］．Mathematics of Computation，1980，35（151）：773－782．

［16］ Likar B，Pernu F．A hierarchical approach to elastic registration based on mutual information ［J］．Image and Vision Computing，2001，19（1）：33－44．

［17］ Klein S，Staring M，Pluim J P W．Evaluation of optimization methods for non－rigid medical image registration using mutual information and b－splines［J］．IEEE Transactions on Image Processing，2007，16（12）：2879－2890．

［18］ Christensen G E，Geng X J，Kuhl J G，et al．Introduction to the non－rigid image registration evaluation project ［R］．Biomedical Image Registration，2006．Springer．128－135．

［19］ Vercauteren T，Pennec X，Perchant A，et al．Diffeomorphic demons：efficient non－parametric image registration［J］．NeuroImage，2009，45（1）：S61－S72．