小波降噪技术在差分吸收光谱浓度检测中的应用

梅魏鹏，余 淼＊，师 翔，王 英，浮 洁，张永彩

（1．重庆大学 光电工程学院 传感器和仪器技术研究中心，重庆400044；2．烟台开发区龙源电力燃烧控制工程有限公司，山东 烟台264006）

目前我国的发电方式仍然以火力发电为主，因此我国是世界上最大的煤生产国和消耗国。与其他能源相比，煤是一种“不干净”的燃料，在燃烧的过程中会产生大量的SO2、NOx气体和粉尘等废弃物，如未能妥善处理，将对我们的环境造成极大的影响。

20世纪80年代初，德国海德堡大学环境物理研究所的Platt和Perner在Noxon的工作基础上提出了基于差分吸收光谱（DOAS）的检测技术并将其成功应用在对流层大气的研究领域［1，2］。基于该原理的装置具有结构简单、实时性能优越、检测精度高等优点。近年来国内外相关学者纷纷将DOAS技术拓展应用于各种工业锅炉、燃煤锅炉等固定污染源排放物的检测上面。在国外，除了Platt和Perner之外，Stutz等人采用了线性最小二乘法与非线性的Levenberg－Marquardt方法，消除了光谱的平移、伸展和压缩对测量结果的影响［3］。比利时的高层大气物理研究所对SO2标准吸收截面的测量做过一系列的研究，他们提出在不同的波长段用傅里叶变换的方法来处理吸收截面［4］。国外的研究多侧重于大气中痕量气体检测。国内的中科院安徽光机所的刘文清团队将DOAS技术成功的应用在大气痕量气体的监测中，理论研究深入，其长光程多轴差分吸收光谱技术较为新颖［5］。天津大学的孙长库团队已经成功的研制出适用于火电厂的插入式测量浓度装置，并成功开发出SO2在线检测①周 涛．烟气排放紫外差分吸收光谱实时监测方法的研究（博士论文）．天津：天津大学测试计量技术及仪器专业，2008．。东南大学的王式民团队对差分吸收光谱法也有比较深入的理论研究，其在温度和压力对吸收截面的影响方面的研究更为突出［6］。

DOAS方法是将利用光谱仪测得的差分吸收结构与标准的吸收截面做最小二乘拟合，从而反演得到待测气体的浓度值。在实际的应用中采集到的光谱信号会受到各种因素的干扰，包括除被测气体之外其他气体的吸收、光谱仪暗电流、各种杂散光以及颗粒物散射等［7］。现有的去噪方法大致有三种：传统傅里叶变换法、平滑去噪法和基于小波变换的去噪方法。其中平滑法主要适用于稳定的信号，平均时间过长，不能作动态提取，并且处理的噪声对象限于白噪声②吕瑞兰．小波阈值去噪的性能分析及基于能量元的小波阈值去噪方法研究（硕士论文）．浙江：浙江大学模式识别与智能系统专业，2003．2－5，12－15．。傅里叶变换适合滤除那些具有近似周期性的波动信号，而对具有显著局部特性的信号无能为力，如果有用信号的高频部分和由噪声引起的高频干扰相互叠加，傅里叶变换便不能有效的将其加以区分。而小波变换法具有良好的时间局部分析能力［8，9］。

1 DOAS检测气体浓度的原理

差分光谱法来测量气体浓度基于修改后的Lambert－Beer定律，即：

其中，ci为被测物质的浓度；L为光程；I0（λ）和I（λ，P，T）分别为光源的光强和经过待测气体后的光强；σi＝σi′＋σib，σi′为随波长快速变化的窄带吸收截面，σib为随波长缓慢变化的宽带吸收截面；A（λ）表示光学系统对波长λ的依赖性；εR（λ）和εM（λ）分别表示 Rayleigh散射和 Mie散射系数。

通过对得到的输出光谱和输入光谱做信号处理，再结合实验室测得的标准吸收截面即可以得到相应的待测气体浓度③邵理堂．差分吸收光谱法在线测量烟气浓度的理论与系统研究（博士论文）．南京：东南大学测试计量技术及仪器专业，2008，24－27．。

2 小波去噪原理

小波变换具有良好的时频局部化性质，因而可以很好的保存有用信号的尖峰和突变部分。小波去噪的原理就是：给定一个信号，首先把它展开成小波的平移和伸缩之和，然后把欲舍弃项的系数去掉或加以适当的修改，由修改后的小波系数做逆向小波变换得到去噪后的信号。

为引入小波变换，设给定一小波函数Ψ（t）∈L2（R）（L2（R）表示平方可积的实数空间，即能量有限的信号空间），其傅里叶变换为＾Ψ（ω）。当 Ψ（x）和 ＾Ψ（ω）分别满足允许条件：

a）Ψ（x）是连续的且呈现指数衰减（即Ψ（x）≤Me－C｜x｜，对某些常量C，M）；

则称Ψ（t）为一个基本小波或母小波，将母小波函数Ψ（t）经伸缩和平移后，就得到一个小波序列。

对函数待处理的信号函数f（t）∈L2（R）的小波变换为CWT（a，b）：R2→R，即：

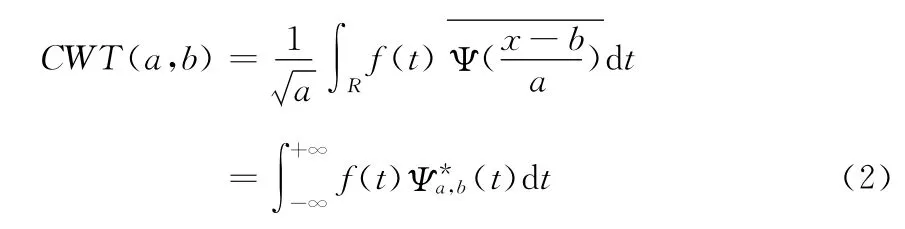
对于离散的情况，对伸缩因子a和平移因子b进行离散处理，则离散小波变换为［10］：

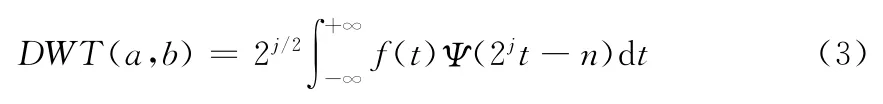
其中，a＝2－j，b＝n2－j，n∈Z。

在对离散混合信号去噪的应用中，可以假设X为离散的输入信号，长度为N，具体分解过程如图1所示（此处仅以3层分解为例）。

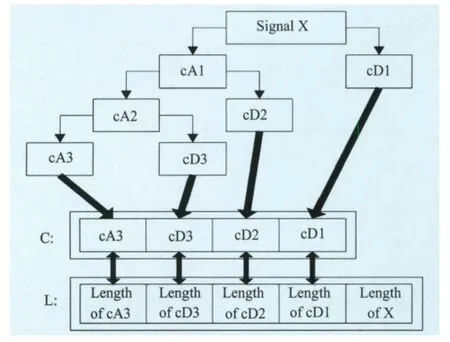
图1 小波分解的原理

含噪信号经小波变换后得到的小波系数分为高频cD1和低频cA1部分，然后再将低频部分cA1进行下一层分解，而高频部分不再分解。含噪信号可以看作由最底层的低频部分和所有层的高频信号组成：

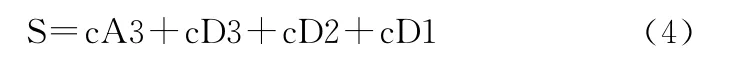
高频部分cD1、cD2、cD3包含信号本身信息和噪声信息，一般情况下，随机噪声的小波系数非常小，这样可以设定一个阈值，对小于该阈值的小波系数置零，然后利用处理后的小波系数重构原信号即可实现降噪［9］。

3 对比实验

在小波分析信号的应用中，存在一个十分重要的难题：分解层数的确定和小波基函数的合理选择，因为针对同一个信号，采用不同的小波基分析或者采用不同的分解层数将会对信号分析产生不同的结果。目前主要通过小波分析处理信号与理论信号的误差来选择最优的小波基。对光谱信号处理比较有效的几种小波系主要包括：Symlets小波系、Daubechies小波系、Coiflet小波系和Biorthogonal小波系。以在工业现场测得的紫外光谱数据作为背景，以在实验室测得的吸收光谱信号为基准，以去噪后的信噪比为指标，利用MATLAB中的几种离散小波系和几种阈值选取方法分别对现场的信号进行小波变换去噪处理实验，从而得到适合本系统的最佳小波去噪方法。

本文中信噪比定义为：

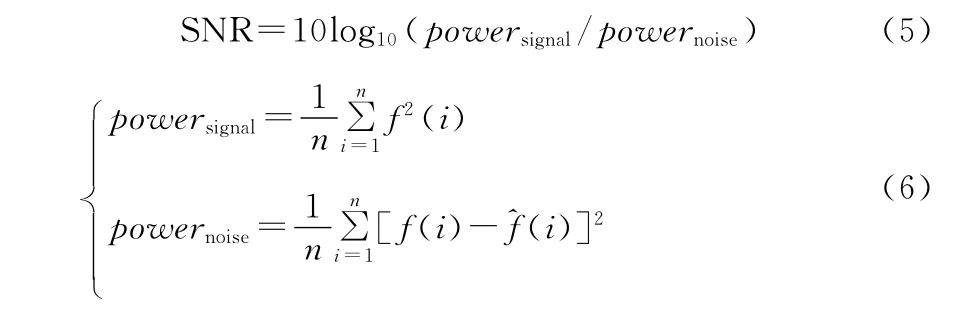
其中，powersignal为真实信号的功率，powernoise为噪声的功率。f（i）为离散的原始信号，为小波滤波去噪后的离散还原信号，n为数据的个数。

按照此定义求得的信噪比的单位为dB（分贝），信噪比越大，则表示去噪的效果越好。

假设在实验室测得的吸收光谱为理想条件下的吸收光谱S，在此基础上添加信噪比为40dB的高斯白噪声N组成新的吸收光谱来模拟在工业现场采集到的光谱信号，并将其表示为Sn，三种光谱分别如图2所示。

利用Matlab工具中的Wavelet Toolbox对复合的光谱信号进行一维离散小波变换，经过小波变换后，幅值较大的小波系数主要为有用信号，幅值较小的则以噪声为主。阈值降噪就是选择适当的阈值，当小波系数大于该阈值时保留，当小波系数小于该阈值时则置零。最后用滤除后剩下的小波系数对信号进行重构，该方法可以完全抑制信号中的白噪声。

图2 由上往下分别是原始光谱、噪声和复合光谱

根据以上分析，分别利用四种小波函数对原始光谱S和复合光谱Sn做小波变换和重构，再对处理后的光谱做相应的处理，得到各自的信噪比SNR＊以及SNR，从而直观的得到最适合本系统的最佳小波函数。

在此，可以假设原始光谱S为一个理想的纯净的信号，即假设其不含任何噪声，由信噪比的定义可知对其进行小波分析重构后的信号噪声比（SNR＊）应该趋于无穷大；而对于含噪信号Sn，由于其存在噪声，故而经过小波分析重构后的噪声存在数值，即信噪比（SNR）定义中的分母不为0，而且比较大，相应的信噪比的值则应该小。从图3中可以直观的看到，对原始光谱S进行小波分解重构滤波后的信噪比（SNR＊）要普遍高于对复合光谱Sn滤波后的信噪比（SNR），这可以间接的证明该方法在原理上是正确的。理论上对原始光谱S滤波后得到的信噪比SNR＊应该是趋于无穷大的，然而SNR＊并不是无穷大说明了该滤波方法存在将有用信号当作噪声滤除的问题，因此SNR＊的数值应该是越高越好；对复合光谱Sn滤波后的信噪比SNR在bior1、db1、sym1处的滤除噪声虽然多，但是在这三种小波函数下滤波的信号失真也比较大，故而不可取。SNR比原始的40 dB的信噪比大，说明滤除的噪声不够完全，在大于40dB时其值越小则表明滤除的噪声越多，滤波效果也越好。

通过对其余四个小波函数进行小波变换得到的SNR可知，单纯的从各自的信噪比出发来判断滤波效果的好坏是片面的，我们既需要保证尽量少的丢失原始光谱信号，又要保证足够多的滤除噪声信号，因此在此构造一个新的评价指数η。

图3 四种小波函数的分解去噪所得信噪比图中横坐标为小波系中小波函数的序号（如在Daubechies小波变换中的横坐标3即表示采用的是“db3”小波母函数，此时的3也表示这个小波函数的消失矩）

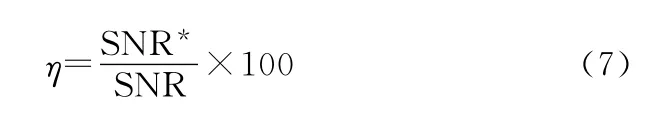
分别将三种小波变换得到的信噪比带入新定义的评价指数计算公式中，得到表1。

从表1中可以看出db10、db11、sym11和sym15更能在满足降低噪声的同时减少有用信号的丢失，这四种小波函数是用来降低系统噪声和Mie散射带来误差的最佳小波函数。利用sym15小波函数对工业现场采集到的光谱信号进行小波重构，效果如图4所示。

小波去噪阈值的选取大致分为以下四种规则：1）通用阈值T1（Sqtwolog规则）；2）Stein无偏风险阈值T2（rigisure规则）；3）试探法的Stein无偏风险阈值T3（heursure规则）；4）最大最小准则阈值T4（minimaxi规则）。在对阈值进行选取时，需要考虑噪声和有用信号的范围，rigisure阈值和minimaxi阈值的选取比较保守，是将部分频率系数置零，信号的高频成分会有一部分在噪声范围内，但是此两种阈值可以将弱小的信号提取出来；而heursure阈值和sqtwolog阈值用在信号去噪的时候更为有效。在实际应用的时候可以根据不同的情况选用不同的阈值。

对信号Sn，分别采用四种阈值消噪，得到的结果对比如表2所示。

从表2中可以看出去采用四种阈值的效果差异并不大，相比之下采用Minimaxi阈值噪后的信号能保证大量滤除噪声的同时保留更多的有用信号，因此Minimaxi阈值比其他另外两种阈值更适合本研究系统。

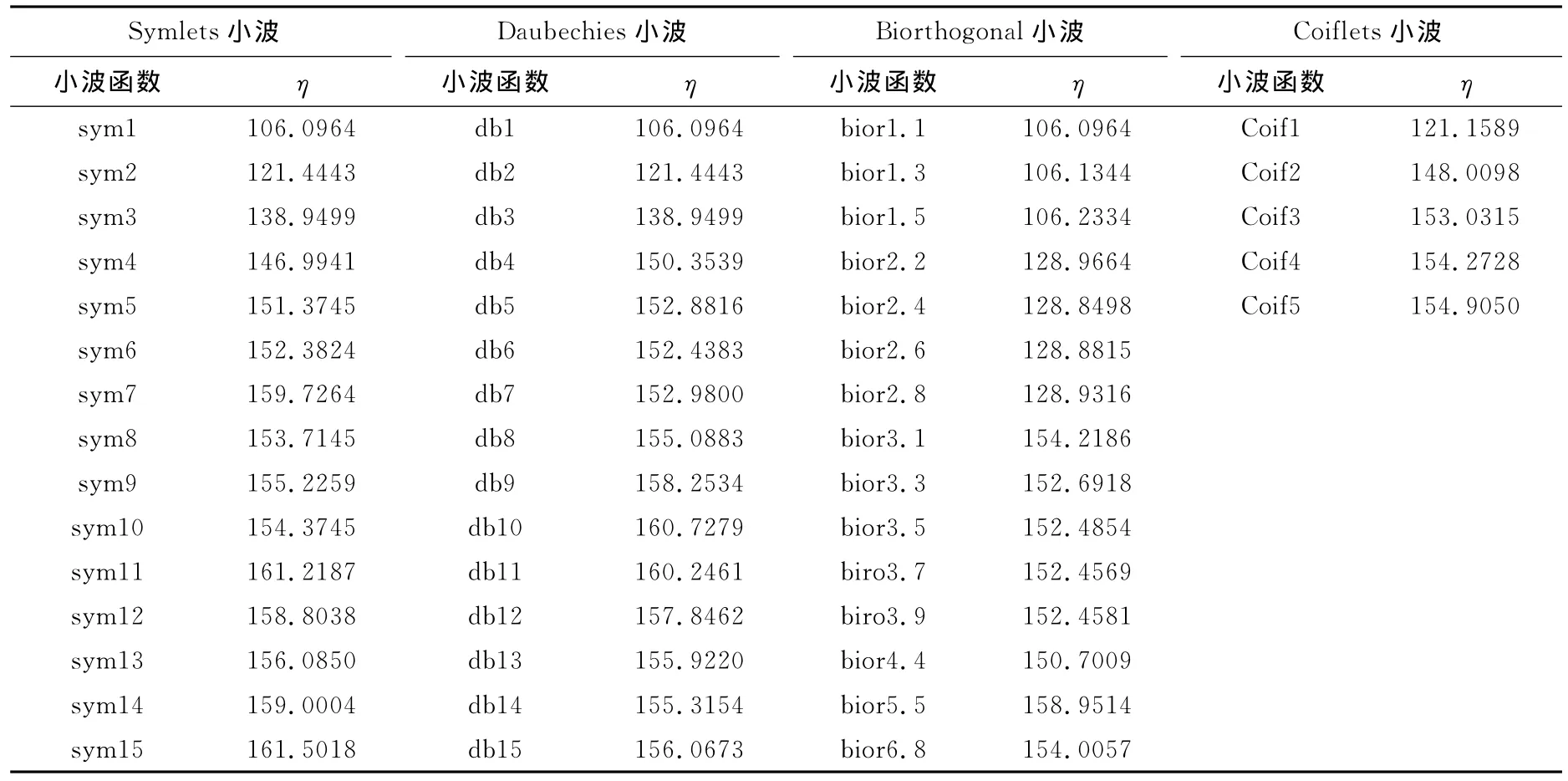
表1 不同小波函数下的参数ηDifferentηin different wavelets in level one

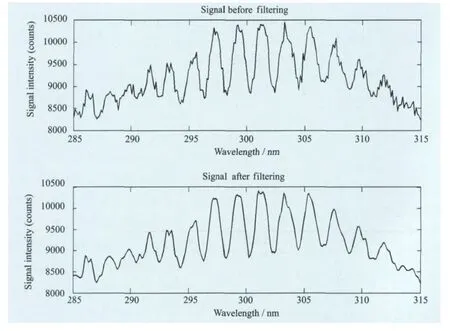
图4 小波重构滤波前后的信号对比

实验是对山东某火电厂烟道中尾气中的SO2气体进行检测，现场与实验室环境相比粉尘浓度更高，振动和噪声也更大。对工业现场采集的光谱数据采用sym15小波函数和minimaxi阈值做滤波处理，处理后的波形如图5所示。

从图5中可以看出，处理后的光谱比处理前的光谱少了很多噪声，可定性的看出去噪效果。

表2 选取四种不同阈值的效果对比Comparison of four thresholds

4 实验结果讨论

现场检测结果如表3所示（其中以现场的岛津仪器采集的数据作为标准数据进行对比）。

此处的相对误差的计算公式为：

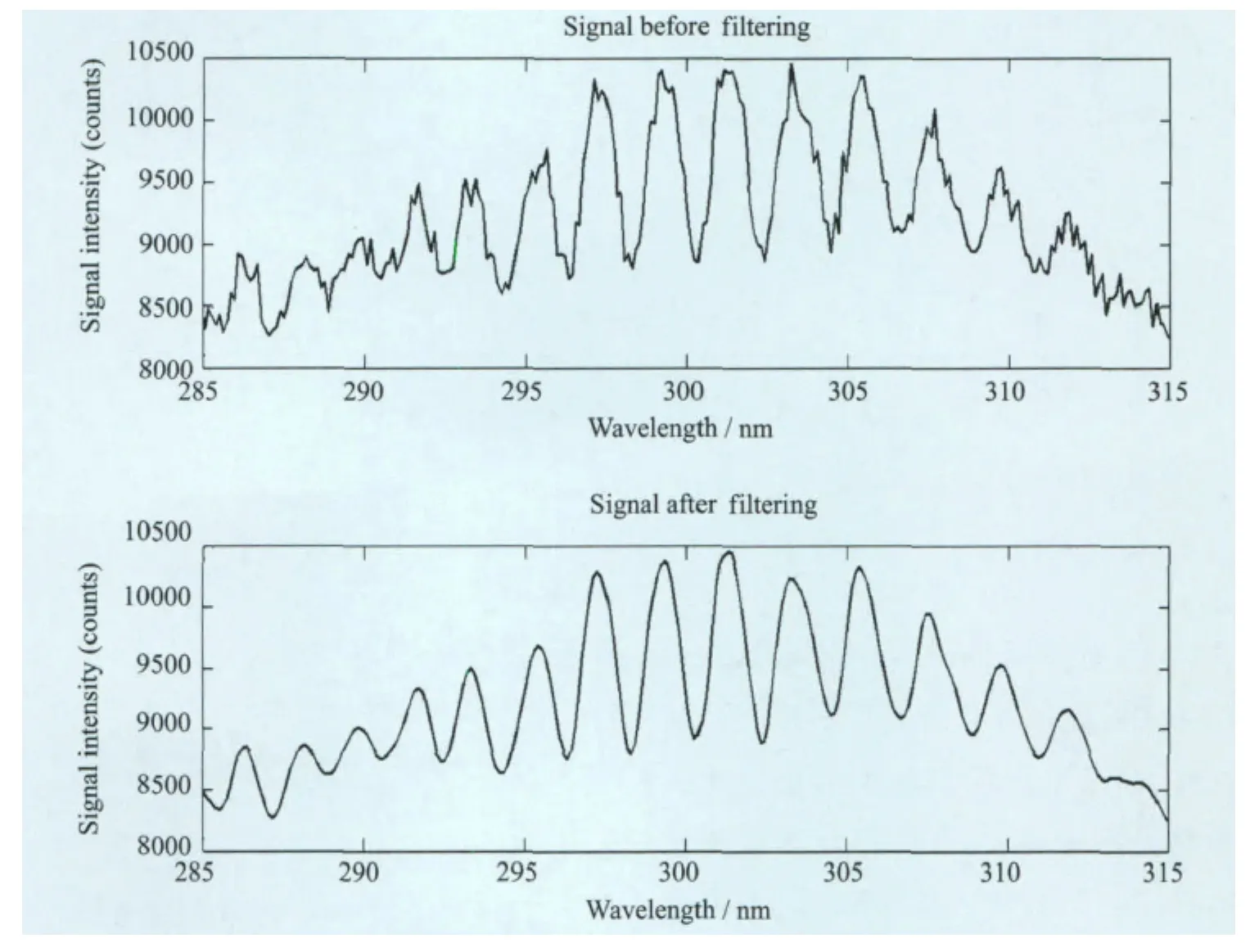
图5 工业现场光谱滤波前和滤波后对比

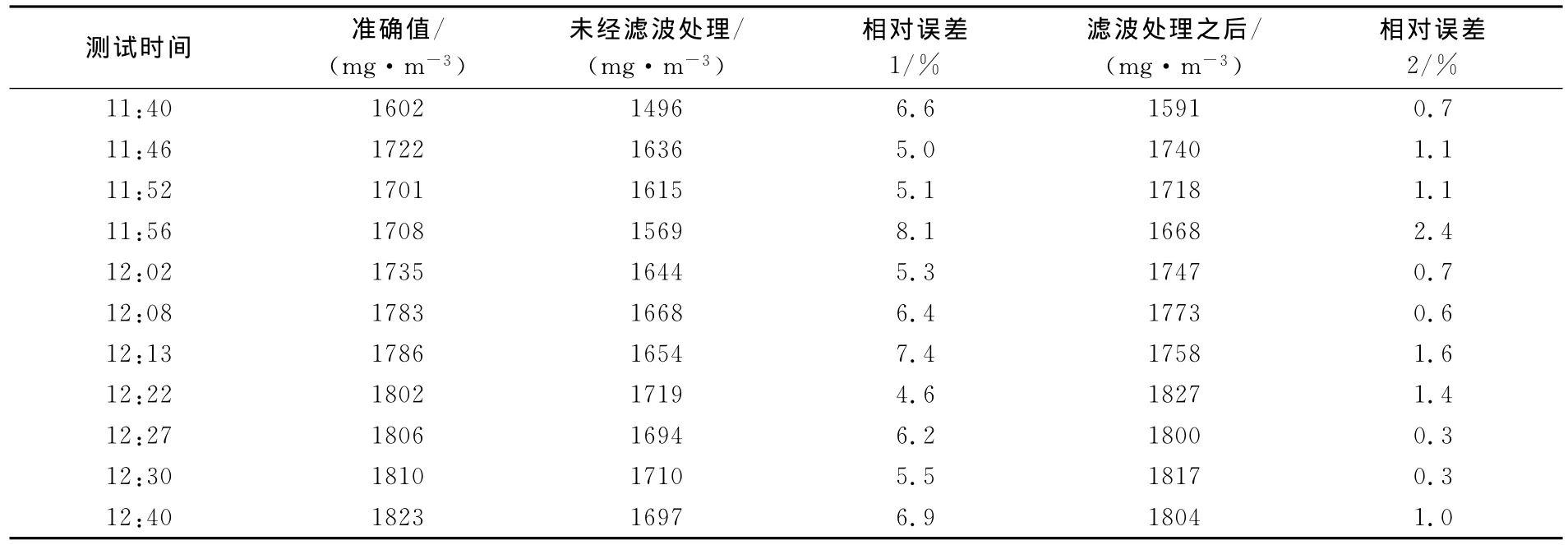
表3 使用小波处理和未使用小波处理的结果数据对比Comparison of results with traditional way and wavelet transform

从表3可知，虽然滤波后测量得到的浓度值相对误差还存在波动，但是误差的绝对值得到了较大的降低，在剔除粗大误差2．4%和1．6%之后，能将准确度基本控制在1．5%以内。相对误差的对比见图6。

5 结论

图6 相对误差对比

在高粉尘和高噪声振动条件下，传统的滤波方法已经无法消除颗粒物散射和系统噪声对吸收光谱的影响，本文提出采用sym15小波函数结合minimaxi阈值来消除散射和系统噪声对浓度反演造成的影响，在山东某电厂的现场实验证明此法在SO2浓度检测系统中是可行的，并且能将测量误差有效的控制在1．5%以内，具有较高的浓度反演精度；然而，此方法存在一定的局限性，虽然对于后续的NOx的浓度测量具有一定的指导意义但却不能生搬硬套，还需根据实际情况选取适当的小波函数和阈值。

［1］ Platt U，Perner D，G W Harris．Detection of NO3in the polluted troposphere by differential optical absorption［J］．Geophysical Research Letters，1980，7（1）：89－92．

［2］ Platt U．Air Monitoring by Spectroscopic Techniques［M］．Switzerland：John Wiley ＆ Sons，1994．31－41．

［3］ Stutz J，Platt U．Numercial analysis and estimation of the statistical error of differential optical absorption spectroscopy measurements with least－squares methods［J］．Applied Optics，1996，35（30）：6041－6053．

［4］ Vandaele A C，Hermans C．Fourier transform measurements of SO2absorption cross sections［J］．Journal of Quantitative Spectroscopy ＆ Radiative Transfer，2009，110：2115－2126．

［5］ 罗宇涵，孙立广，刘文清．采用MAX－DOAS观测北极新奥尔松地区夏季NO2的柱浓度与垂直分布［J］．光谱学与光谱分析，2012，32（9）：2336－2340．Luo Y H，Sun L G，Liu W Q．MAX－DOAS measurement of NO2column densities and vertical distribution at Ny－alesund，artic during summer［J］．Spectroscopy and Spectral Analysis，2012，32（9）：2336－2340．

［6］ 邵理堂，汤光华，许传龙．利用小波变换消除颗粒物Mie散射对DOAS技术的影响［J］．东南大学学报，2008，38（3）：444－448．Shao L T，Tang G H，Xu C L．Eliminating Mie scattering influence of particles on DOAS technique using wavelet transform［J］．Journal of Southeast University，2008，38（3）：444－448．

［7］ 原育凯．光学系统杂散光的消除方法［J］．大气与环境光学学报，2007，2（1）：6－10．Yuan Y K．Stray light suppressing measure of optical system ［J］．Journal of Atmospheric and Environmental Optics，2007，2（1）：6－10．

［8］ 孙延奎．小波分析与应用［M］．北京：机械工业出版社，2005．217－244．Sun Y K．Analys is and Application of Wavelet［M］．Beijing：China Machine Press，2005．217－244．

［9］ 方勇华，孔 超，兰天鸽．应用小波变换实现光谱的噪声去除和基线校正［J］．光学精密工程，2006，14（6）：1088－1092．Fang Y H，Kong C，Lan T G．Denoising and baseline correction of spectrum by wavelet transform［J］．Optics and Precision Engineering，2006，14（6）：1088－1092．

［10］ Albert Boggess，Francis J Narcowich．小波与傅里叶分析基础［M］．第二版．北京：电子工业出版社，2011．9－10，293－296．Albert Boggess，Francis J Narcowich．A First Course in Wavelets with Fourier Analysis［M］．Second Edition．Beijing：Publishing House of Electronics Industry，2011．9－10，293－296．