盲反卷积去噪在机车走行部故障分析上的应用*

于天剑，陈特放，陈雅婷，陈春阳

(1.中南大学交通运输学院，湖南长沙410075;2.中南大学信息科学与工程学院，湖南长沙410075)

在机车的故障诊断和故障预测当中，齿轮的健康是典型的指标，从振动信号中提取这些值进行诊断和预测，可以分析齿轮的剩余可用年限。然而在机车运行当中，振动信号往往有多个激励源，在大多数情况下，由于噪声信息的存在，组成不同来源的综合效果，噪声信号会比真实信号质量下降很多，因此诊断和预后的方法显得尤为重要，如检测阈值时，剩余可使用年限的准确性组件，对机车牵引齿轮进行在线振动监测，并据监测结果诊断出其故障类型及故障程度，是非常必要的。寻找一个高效的，可靠的去除噪声的算法是非常重要的，为尽可能的提取出故障特征的信号，现在广泛使用的消噪技术是同步时间平均(TSA)的方法［1－2］，采样收集的数据存在不同的旋转插值，TSA的技术在频域内被提出来。由于大幅减少了计算，一些功能被成功提取出来并应用在故障诊断当中，由于旋转的齿轮是异步的，在同一时间非常容易受外部随机干扰和噪声，在频域内可能是一些噪声分量出现在频率轴上，并且出现的噪声是频率的倍数，这样会更加增强TSA处理，因此为了实现更好的信噪比和改善TSA数据的质量，提取更准确的特征值，收集更精准来自换能器的振动信号［3－4］，在本文中，采用盲反卷积的数学算法，并用振动分析，非线性投影，成本函数优化作为支撑，针对不断变化的操作系统以实现更好的信噪比，以盲反卷积算法为基础并在真正列车中进行试验验证，结果表明，所提出去噪方案可以大大提高信噪比、功能性能和故障预测算法的精度。所开发的算法已成功应用于实时故障诊断和故障预测［5］。

1 去噪方案原理与设计

盲反卷积整体去噪结构图如图1所示，将传感器安装在变速器上收集振动信号，进行预处理以获得TSA信号S(t)，盲反卷积算法在频域内进行，将此算法用于S(f)中，其输出为去噪的振动源信号B(f)。B(f)再经过逆傅里叶变换得到b(t)，从B(t)和b(t)进行特征提取和融合，随后进行故障诊断和故障预测，此算法不仅可以预测齿轮的剩余使用寿命(RUL)，而且还可以对齿轮裂纹长度做估计，将估计的裂纹长度和负荷曲线输入到振动模型当中，可以产生模型信号m(t)，将m(t)的频谱进行归一化获得加权系数向量W(f)中，可以得到该算法的非线性投影［6－7］。

图1 整体结构去噪方案Fig.1 Structure of the program de－noising

图2为盲反卷积的去噪方案，在此结构中非线性投影是基于在振动信号上分析的，成本函数优化是关键的组成部分。降噪方法首先是把测得的振动信号s(f)，经过傅里叶变换送入滤波器z(f)中，在频域中信号调制的估计值的倒数，与测得的振动信号S(f)，经过卷积得到信号B(f)，该信号通过非线性投影得到Bnlf，Bnlf和B(f)可以表示为E(f)，对其进行优化的方法是取E(f)信号并得到极小值，即－B(f)可视为去噪，经过逆傅里叶变换，在时域内可以通过以下方法获得降噪后的信号［8］。

图2 盲反卷积去噪Fig.2 Blind deconvolution de－noising

图3 一个齿轮的系统配置Fig.3 System configuration of a gear

2 系统设计

振动信号从列车的变速器变速箱上提取出来，由于齿轮数过多，以经典的5齿轮进行研究［9］，如图3所示，分析一个假设的理想系统，加速度传感器被安装在固定的点上，该位置θ=0。所观察到的齿轮振幅大时，则齿轮接近传感器，小时则远，假设只有一个齿轮，然后在振动具有最大幅值的时候，此时 θ=0，2π，4π，同样信号具有最小振幅的时候是在 θ=π，3π，...，在理想状态下，齿轮N=5个的齿轮均匀转动，并假定转动频率为fs后，此时刻t与齿轮的相位为

这种情况下，齿轮的调制信号p在时域内可写为:

其中:N是谐波数量;αn是调制信号频率为nfs的振幅，在理想情况下，所有的齿轮产生信号具有相同的幅值，但相位不同，由于齿轮的速度正比于角速度，齿合振动频率出现为，另外在频域中，其振动信号具有谐波振幅为βm，则振动齿轮p产生的信号可以表示

然而，静态加速度计下其振动信号p作为齿轮源信号与振动信号的合成，可以给定为:

当有一个以上的振动信号时，用加速度计所观察到的振动信号则是所有信号的叠加:

如式(1)中所示，对于健康的齿轮，任何整数k满足 sin(2kπ + θ)=sinθ，如式(5)所示，mNt+n是否为Np的倍数，若不能整除则有余数为γ，振动信号在不同齿轮所均匀分布的角度为2γπ/Np，如图4所示，在Np=5的情况下表示了其是否为Np整数的叠加图，如果mNt+n不是Np的倍数也就是有余数，情况不同的振动齿轮相结合时这些频率分量会加在边带频率上，这种情况判断为故障;相反，如果mNt+n是Np的倍数，那么会产生对称的频带如图4(b)所示，其中 ξp，m，n是在1 ≤ p≤5 情况下的频率分量［10－11］。

图4 健康和故障齿轮Fig.4 Health and failure respectively gear

研究结果表明，在一个理想系统中，齿轮数是频率的倍数，然后可以将其傅里叶变换写成:

γm，n为频谱幅值的大小，fnl是其非线性投影，

当齿轮上有一条裂纹的时候，此时齿轮不再沿2π均匀地隔开，由于这个相移如果mNt+n不是Np的倍数时，不同齿轮的振动分量不会消除，这个结果将会导致更高的非啮合频率;另一方面，如果mNt+n是Np的倍数，不同的振动分量会有不完全的相位，这将导致非啮合频率的降低，如图4所示。因此非线性方法不适合来预测有故障的变速箱，故我们可以修改为在频域内，振动模型将已经确立负荷分布和裂纹的大小作为2个输入端，负载曲线可以从已知裂纹尺寸的预测算法来估计，改进的模型如图1和图2所示，这种情况下可以得到非线性投影为

3 盲反卷积去噪计划

从齿轮箱的振动分析可知，振动信号是由多个信号所组成的，为了简化模型，这样一个复杂的信号被定义为:

其中:s(t)为测试的振动信号;b(t)为无噪声的未调制的振动信号;a(t)是调制信号;n(t)是累积的加性噪声。此时，在系统中，调制信号a(t)的本身

因此，式(9)可以表示为

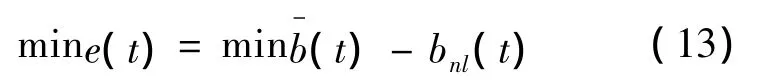
以前的研究结果为旋转设备振动信号的光谱特性，因此，由频域卷积定理可知，测得的振动信号在时域上的积等同于2个信号在频域中的卷积，所以式(10)在频域内可以写为

最后到时域转换回恢复无噪声振动信号

Dsup是包含了主要振动信号的频率范围，由于存在谐波并把谐波集中在一个窗口来定义临界频率，所有这些窗口都在Dsup内，在式(18)中假设(1)和(2)将用于第2项中用来避免全0的逆滤波器Z(f)，可以使误差最小化，此外，用迭代的方法具有更快的收敛性［12－14］。

4 试验结果

为了能更好地进行准确度和精确度的分析，提出了2个性能指标使其能更直观的体现试验的有效性，第1个性能指标为线性关系特征值和裂纹增长曲线，其中x为特征向量，y为裂纹生长曲线，可以表示为

式中:lx为其数量，xi为是平滑的特征向量。是由边带的特征向量。在故障的预测和检测算法中，提取特征值被作为测量输入的，因此性能指标和检测阈值和精度的预测其使用寿命是密切相关的，一个精确的PMD特性都应该有一个很小的值近乎为0。

图5 不同方法的去噪对比Fig.5 Comparison of different methods of de－noising

图5所示为不同的运行周期下去噪的情况，可以明显地看到，盲反卷积去噪具有最高的信噪比，故其方法是可行的，而在不同扭矩下不同的相关系数和PMD比值总结在表1中。可以观察到在100%扭矩下，CCR，CCS和PMD在TSA和D－N去噪数据分别为 0.953，0.971 和 5.57% 以及0.983，0.991和3.57%，可以看出 D －N 和 TSA 去噪相比，精度几乎是相同的，但是从性能指标上有明显的改善，由此可以看出去噪算法的作用。

表1 不同转矩下的精度与性能指标Table 1 Aerodynamic drag coefficient of each part of head car

5 故障预测

对于向前一步的预测，可以使用经验数据来估计RUL，该算法的实现需要一个过程模型，因此，下面为去裂纹的生长状态模型和模型参数估计。

其中:L(t)为裂纹的生长曲线;w1(t)为非高斯白噪声信号;α(t)为未知参数模型;w2(t)为另一个非高斯白噪声;C和M分别为固有材料的特有常数;ΔK(t)是对于裂纹长度和应力的负荷分布;f为一个非线性裂纹受力变化情况;h为裂纹增长预估计值［12－14］;v(t)为被干扰的非高斯白噪声，也就是在2个循环内运行此算法，内环更新可以对该功能的数据裂纹长度做估计，外环更新非线性映射到h当中，这样长期预测每个粒子生成的估计状态，这些估计值可以在任何时间段内估计RUL和PDF(概率密度函数)。由实验可以得到运行周期与裂纹大小情况，如图6所示。

图6 运行周期与裂纹大小情况Fig.6 Peration cycle and the size of crack

表2 不同方法下的准度与精度Table 2 Accuracy and precision of the different method

以第714个周期时裂纹大小和期望作为对比，比较前后消噪情况可以得出此算法的效率，可以用可信区间(CI)和期望来预测故障概率，信任区间更多可以和第714个运行周期做比较，小于95%CI即更为精确，，而期望则是越靠近714个周期越准确，更多实验数据如表2所示。表2所示准确度的改进是TSA的信任区间减去D－N的信任区间的长度，而精确度为714减去真值的期望，越接近于0效果越好。在第365个周期的时候，准确度和精度是十分相似的，在第400个周期的时候两者都有提升，其信任区间长度是41个周期，在此结果上其期望为747，超出了714个周期，故效果一般，另一方面消噪的效果非常接近714个周期，在第450个周期的情况下，其效果和第400个周期十分相似，但是效果要好于第400个周期的时候，故起到了预测的作用。

6 结论

(1)在实际的检测当中，高质量的振动信号往往被噪声和干扰所掩盖掉，本文介绍了一种新的振动信号去噪的模型，用新模型与特征提取以及故障预测的共同作用的方法，来提高信噪比和信号质量，并且提高对该故障预测的准确度和精度。

(2)从数据的准确度和精度方面与TSA去噪方法和谱减法进行比较，信噪比和性能指标的试验结果表明盲反卷积去噪比常规去噪更有效率，这样的信号处理技术明显降低了故障检测阈值，提高了诊断和预警的技术。

(3)在高速列车当中，盲反卷积去噪计划是很实用的方法之一，可以应用到各种系统中，特别是在非线性系统中的开发有很大的研究价值。

［1］Kam Z，Feuer A.Blind image deconvolution using machine learning for three － dimensional microscopy［J］.Mech Pattern Analysis and Machine Intelligence，IEEE Transactions，2010，32:2194 – 2204.

［2］Onel I Y，Benbouzid M.Induction motor bearing failure detection and diagnosis:Park and concordia transform approaches comparative study［J］.IEEE/ASME Trans Mechatronics，2008，13(2):257 – 262.

［3］Lankarany M，Savoji M H.Knowledge based blind deconvolution of non － minimum phase FIR systems［J］.Electrical and Computer Engineering Conference，2010，10:1 －5.

［4］Keller J，Grabill P.Vibration monitoring of UH － 60A main transmis － sion planetary carrier fault［J］.Amer Helicopter Soc 59th Annu Forum Phoenix，AZ，2003:1 －11.

［5］曹尧谦，李夏苗.基于改进四阶段法的武广客运专线客流预测［J］.铁道科学与工程学报，2010，7(3):109－114.

CAO Yaoqian，LI Xiamiao.Based on four－stage method of Wuhan－Guangzhou Passenger Railway Line and prediction［J］.Journal of Railway Science and Engineering，2010，7(3):109 －114.

［6］苏文胜.滚动轴承振动信号处理及特征提取方法研究［D］.大连:大连理工大学，2010.

SU Wensheng.Rolling bearing vibration signal processing and feature extraction method［D］.Dalian:Dalian University of Technology Electrical and Mechanical College，2010.

［7］Orchard M.A particle filtering－based framework for online fault diagnosis and failure prognosis［D］.Georgia Inst Technol，Atlanta，2007.

［8］Wu B，Saxena A，Khawaja T，et al.An approach to fault diagnosis of helicopter planetary gears［J］.Autotestcon，San Antonio，2004:475－481.

［9］LI Lianlin，WANG Libo，TAN Yunhua.Generalized MED blind deconvolution of GPR data and its sparsity－promoted solution［J］.MicrowaveConferenceProceedings(APMC)，2013:1024－1026.

［10］程军圣，杨宇.局部均值分解方法及其在齿轮故障诊断中的应用［J］.振动工程学报，2009，22(1):76 －84.

CHENG Junsheng，YANG yu.Local mean decomposition method and its application in gear fault diagnosis［J］.Journal of Vibration Engineering.2009，22(1):76 －84.

［11］王洪霞，李学平，含表面裂纹悬臂梁的非线性振动分析［J］.铁道科学与工程学报，2010，7(1):69－73.

WANG Hongxia，LI Xueping，Nonlinear vibration analysis of a cantilever beam with surface cracks［J］.Journal of Railway Science and Engineering，2010，7(1):69 －73.

［12］Antoni J.Blind separation of vibration components:Principles and demonstrations［J］.Mech Syst Signal Process，2005(19):1166－1180.

［13］Sroubek F，Milanfar P.Robust multichannel blind deconvolution via fast alternating minimization［J］.Image Processing，IEEE Transactions on，2012，21(4):1687 －1700.

［14］Li L.Sparsity－Promoted Blind Deconvolution of Ground－ Penetrating Radar(GPR)Data［J］.Geoscience and Remote Sensing Letters，IEEE，2014(11):1330 －1334.