永磁同步牵引电机有效磁链观测及转矩控制*

赵凯辉，陈特放，张昌凡，何静，黄刚

(1.中南大学交通运输工程学院，湖南长沙410075;2.湖南工业大学电气与信息工程学院，湖南株洲412007;3.中南大学信息科学与工程学院，湖南长沙410075)

永磁同步电机(Permanent magnet synchronous motor，PMSM)以其高功率因数、高功率密度、强过载能力、优越的调速控制性能［1］，能够实现低速恒转矩、高速恒功率运行，能在全部转矩范围内提供大而准确的转矩等优点受到轨道交通牵引系统研发人员的高度重视。“节能、环保、经济”的永磁同步牵引系统已成为下一代轨道交通牵引传统系统的发展方向［2－3］。轨道牵引驱动控制系统要求电机控制系统转矩控制的精度在给定5%范围内［4］。有效准确地检测或观测电机的输出转矩，构成转矩反馈闭环控制才能按照给定指令值输出相应的转矩而实现转矩控制。因负载转矩的直接测量成本较高，并且受仪器精度和响应速度的影响较大，因而转矩在线观测是现实的解决方案。

郑泽东等［5－7］提出了表贴式永磁同步电机基于Kalman滤波器的负载转矩观测器，利用观测的负载转矩形成对给定转矩的前馈补偿，改善负载转矩波动过程中的转速控制性能。朱元等［8］基于模型参考自适应方法对永磁体磁通进行辨识，估计永磁同步电动机的转矩值，形成转矩闭环控制。ZHANG等［9］使用滑模控制的方法实现了永磁同步电机负载转矩的观测。滑模变结构控制［10－11］对系统参数摄动、外界扰动及数学模型不准确具有很好的鲁棒性，但传统滑模控制的抖动现象限制了其应用。终端滑模［12］(Terminal Sliding Mode，TSM)控制通过设计非线性滑模面可获得有限时间收敛特性，但存在奇异问题。冯勇等［13－15］提出一种非奇异终端滑模(Nonsingular Terminal Sliding Mode，NTSM)，解决了传统终端滑模中的奇异问题，且稳态跟踪精度高。Levant［16］提出了高阶滑模控制的方法，将高频切换控制加到滑模变量的高阶导数上，有效消除了抖振，同时保留传统滑模的良好特性。

本文采用矢量控制技术，基于PMSM有效磁链的概念，在α－β坐标系中构建了龙贝格－滑模自适应滑模观测器，准确估计出定子电阻和q轴电感并作为有效磁链观测器的输入;同时，在α－β固定坐标系中设计了一种观测永磁电机有效磁链的非奇异终端滑模，并基于滑模等值控制方法实现了有效磁链观测，进而进行转矩的实时估算，和给定转矩形成转矩闭环控制，从而实现PMSM转矩的精确控制。该方法不仅适用于表贴式永磁同步电机(surface－mounted permanent magnet synchronous motors，SPMSM)，而且适用于内置式永磁同步电机(Interior Permanent magnet synchronous motor，IPMSM)。仿真结果表明，该观测器具有较高的观测精度和良好鲁棒性，有效地抑制了抖振，可实时准确地检测有效磁链和转矩，提高了控制系统转矩控制的精度和鲁棒性;仿真结果验证了方法的可行性和有效性，该方法更适于工程实际应用。

1 基于有效磁链的IPMSM数学模型

α－β坐标系中PMSM的电压方程为:

式中:uα和uβ分别为α－β坐标系定子电压分量(V);iα和iβ分别为α－β坐标系定子电流分量(A);Rs为定子电阻(Ω);ψα和ψβ分别为α－β坐标系定子磁链分量(Wb)。

d－q旋转坐标系PMSM的电压方程为

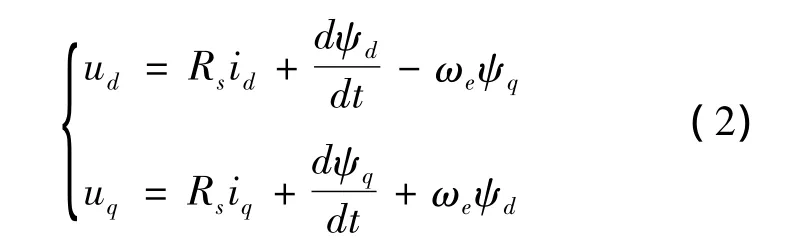
内置式永磁同步电机在d－q旋转坐标系中的定子磁链方程为

将式(3)代入式(2)，由于永磁体磁链变化相对于电流变化较为缓慢，在一个控制周期内可以看作不随时间变化，即其变化率dψr/dt=0。以定子电流作为状态变量，可得永磁同步电机d－q坐标系下的电流状态方程

d－q坐标系中的电磁转矩方程

式(2)～(5)中:Ld和Lq分别为定子绕组的d和q轴电感(Wb);ud和uq分别为定子绕组的d和q轴电压(V);id和iq分别为定子绕组的d和q轴电流(A);ψr为转子永磁体磁链(Wb);当Ld=Lq=Ls时，即为表贴式永磁同步电机。

1.1 有效磁链的概念

定义有效磁链(active flux)［17－22］为

此时转矩方程(5)可表示为

由式(3)可得

有效磁链ψext在d－q旋转坐标系中分量为

由式(9)可知，有效磁链矢量 ψext与d轴同向［19］。如图1 所示。

图1 有效磁链Fig.1 Active flux in coordinate frame

从图1可知有效磁链ψext在α－β为静止坐标系分量为

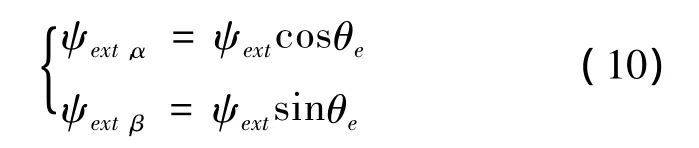
将式(8)变换到α－β坐标系可得有效磁链和定子磁链的关系为

1.2 基于有效磁链的IPMSM数学模型

将式(11)代入式(1)，IPMSM电压方程变为

由于机械系统时间常数远远大于电气系统的时间常数，由式(10)可得

将式(13)代入式(12)，以定子电流作为状态变量，IPMSM模型可表示为

可见基于有效磁链的 IPMSM方程(14)和SPMSM方程具有同样的形式，方程(14)仅与定子电阻 Rs和 q轴电感 Lq2个参数有关，减少了IPMSM对直轴电感参数的依赖性，消除了电机凸极现象。

2 基于龙贝格－滑模观测器的自适应参数辨识

2.1 龙贝格－滑模观测器设计

为了准确辨识定子电阻Rs和q轴电感Lq，基于式(15)设计参数自适应的龙贝格—滑模观测器为［23］:

式中:a＞0，a用来调整Sigmoid函数的斜率。采用连续的Sigmoid函数代替传统的开关函数进行滑模变结构控制，可有效地减小传统滑模观测器带来的抖振现象。

龙贝格—滑模观测器等效控制后得到的是有效磁链的实际值和估计值之间的误差量，而不是其估计值，其目的是为了构造模型参考自适应系统的参考模型和可调模型，从而提取定子电阻Rs和q轴电感Lq信号。所设计的观测器如图2所示。

图2 参数自适应龙贝格－滑模观测器Fig.2 Luenberger－ sliding mode observer of parameter adaptation

用式(15)减去观测方程(16)，可得误差动态方程为

2.2 稳定性证明及自适应律

为考察观测器(16)的收敛情况，构造Lyapunov函数

假设定子电阻Rs和q轴电感Lq变化率远小于电流的变化率，所以可以在一个周期认为a和b为常数。对式两边求导可得

把式(20)分成3项，并令第2项和第3项为0:

由式(22)和(23)可得a和b的自适应律

所以可得定子电阻Rs和q轴电感Lq的估计值为:

为使观测器稳定，选择观测器增益矩阵使式(21)的右边第1项为半负定，利用极点配置的方法使其在左半平面。只需考虑其右边第2项。

于是

由式(22)，(23)和(30)可知˙V＜0。由Lyapunov稳定性理论可知，所设计的观测器全局范围渐进稳定。

3 有效磁链非奇异终端滑模观测器设计

3.1 有效磁链非奇异终端滑模观测器的构造及稳定性分析

为了提高观测器的精度，并抑制控制量的抖振，采用非奇异终端滑模观测器观测有效磁链。对式(15)描述的对象构造如下观测器

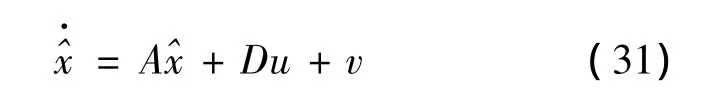
由式(15)减式(31)可得观测器的误差动态方程:

根据高阶滑模控制原理可知，系统(31)对滑模s的相对阶为1，通过二阶滑模可以实现控制量v的平滑无抖振控制，并能使滑模变量s能够到达二阶滑模运动。

选取如下二阶非奇异终端滑模面［13］:

式中:l∈R2，s=［s1s2］T=e，β =diag(β1，β2)，β1＞0，β2＞0为常数，p和q为奇数，且1＜p/q＜

注1 非奇异终端滑模面l用于实现二阶滑模控制，并抑制抖动，当l收敛到0，s和将在有限时间收敛到0，系统到达二阶滑模运动状态并保持在上。

定理 对于电流误差系统(32)，如果选取非奇异终端滑模面(33)，设计式(34)～式(36)的控制律，则系统在有限时间内收敛至0。

其中

证明:选取Lyapunov函数为

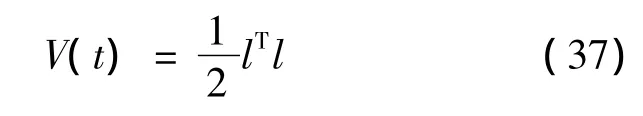
式(37)两边对时间求导得

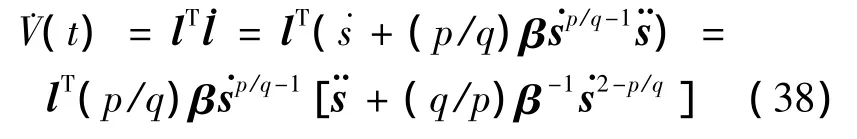
由误差动态方程(32)可得

将式(39)代入式(38)得

进一步可得:

式(40)存在下面3种状态:

由以上可知，误差方程(32)将渐近收敛到0。

注2 所设计的控制律式(34)～式(36)由可测量变量组成，且开关函数加在了控制变量vn的一阶导数上，有效地抑制了控制量的抖振。

注3 可以通过选择参数β，p和q调节收敛速度。到达滑模面l=0。

3.2 有效磁链及转矩观测

即可得到等效的定子有效磁链在α－β坐标系中的分量为

于是可得等效的有效磁链为

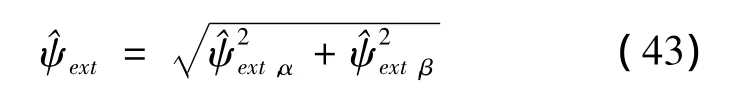
把观测到的有效磁链和定子电流代入式(7)，即可得估计的转矩为

4 仿真及分析

图3为基于有效磁链的永磁同步电机转矩闭环控制系统，主要包括位置速度检测模块、转矩环、电流环、坐标变化模块、空间电压矢量(SVPWM)模块和逆变模块。该控制结构中外环采用转矩闭环，给定的转矩与估计的转矩通过转矩调节器输出交轴给定电流。本文采用控制策略。

图3 基于有效磁链的转矩闭环控制系统Fig.3 Structure of torque closed － loop control system based on active flux

龙贝格－滑模观测器根据定子电压uα和uβ和定子电流iα和iβ以及位置与速度传感器检测到的转子电角速度ωe和转子电角度θe估算定子电阻和交轴电感并作为有效磁链观测器的输入;有效磁链非奇异终端滑模观测器根据电压uα和uβ，电流iα以及iβ和转子电角速度ωe计算有效磁链，进而实时估计电动机转矩，和转矩给定信号构成闭环控制系统，实现转矩精确控制。

仿真所用大功率内置式永磁同步牵引电机参数为:电阻 Rs=0.02 Ω，定子电感 Ld=0.002 370 H，Lq=0.003 572 H，转子磁链 ψr=0.892 Wb，转动惯量J=100，极对数为4，直流侧母线电压1 500 V。

为验证观测器的鲁棒性，设置转速初始值为35 rad/s，0.2 s增加为 200 rad/s;设转矩给定值为500 Nm，在0.4 s增加为1 000 Nm;定子电阻初始值为0.02 Ω，在 0.6 s增加为 0.04 Ω。交轴电感初始值为0.003 572 H，在 0.8 s增加为0.007 144 H。

图4为定子电阻的给定值、观测值及观测误差;图5为q轴电感的给定值、观测值及观测误差。从仿真结果可知，自适应的龙贝格－滑模观测器能很好地跟踪转子电阻和q轴电感。0.2 s时转速增加对电阻和q轴电感的观测结果影响很小。0.4 s时转矩增加对电阻观测结果影响较大，但很快达到稳态，对电感观测结果影响很小。0.6 s时电阻增加到0.04 Ω，电阻的变化对电感观测结果基本没有影响。0.8 s时q轴电感的变化对电阻观测结果影响较大。

图4 定子电阻给定值和观测值以及观测误差Fig.4 Given，observation value and error of stator resistance

图5 q轴电感Lq给定值和观测值以及观测误差Fig.5 Given，observation value and error of q － axis inductance

图6为转矩的给定值、观测值及观测误差，从图中可以看出，转矩观测误差为8‰，满足转矩控制的精度在给定5%范围内的要求。0.8 s时q轴电感的变化对转矩观测结果影响较大，但很快达到稳态。

图6 转矩给定值和观测值以及观测误差Fig.6 Given，observation value and error of torque

图7 有效磁链观测值ext，αext，β 和extFig.7 Observation value active fluxxt，α，ext，β，ext

图8 有效磁链轨迹Fig.8 Observed trace of active flux

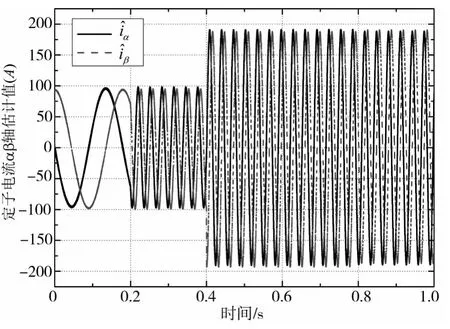
图9 电流观测值和Fig.9 Observation value，

5 结论

(1)采用有效磁链的概念，建立了基于有效磁链的永磁同步电机数学模型，结合龙贝格观测器收敛速度和估计精度可以直接控制的特点和滑模观测器对电机参数摄动、外界扰动及数学模型不准确具有很好的鲁棒性的特点，在α－β坐标系建立了观测电机定子电阻和q轴电感龙贝格－滑模自适应观测器。

(2)在α－β坐标系构建了有效磁链非奇异终端滑模观测器，根据观测的有效磁链和定子电流估算实际的转矩，以此和转矩给定值形成精确转矩闭环控制，提高轨道交通驱动系统的转矩控制精度，改善了轨道交通控制系统的性能。

(3)所设计观测器结构简洁，对电机参数依赖较少，该方法不仅适用于表贴式永磁同步电机，而且适用于内置式永磁同步电机。

［1］揭贵生，马伟明.考虑转子磁通谐波的永磁同步电机控制性能分析［J］.铁道科学与工程学报，2005，2(6):92－97.

JIE Guisheng，MA Weiming.The controlling performance analysis of the PMSM taking into consideration of the rotor flux harmonics［J］.Journal of Railway Science and Engineering，2005，2(6):92－97.

［2］Matsuoka Koichi.Development trend of the permanent magnet synchronous motor for railway traction［J］.IEEJ Transactions on Electrical and Electronic Engineering，2007，2(2):154－161.

［3］Feng J H，Gui W H，Xu J F，et al.Compare of permanent magnet synchronous motor applied to railway vehicle traction system［C］//ICIEA 2007:2nd IEEE Conference on Industrial Electronics and Applications，Harbin，China，2007:74－77.

［4］Sebastian T.Temperature effects on torque production and efficiency of PM motors using NdFeB magnets［J］.IEEE Transactions on Industry Applications，1995，31(2):353－357.

［5］郑泽东，李永东，Fadel Maurice，等.基于扩展Kalman滤波器的PMSM高性能控制系统［J］.电工技术学报，2007，22(10):18 －23，29.

ZHENG Zedong，LI Yongdong，Fadel Maurice，et al.High performance PMSM control system based on extended kalman filter［J］.Transactions of China Electrotechnical Society，2007，22(10):18 －23，29.

［6］郑泽东，李永东，肖曦，等.永磁同步电机负载转矩观测器［J］.电工技术学报，2010，25(2):30－36.

ZHENG Zedong，LI Yongdong，XIAO Xi，et al.Load torque observer of permanent magnet synchronous motor［J］.Transactions of China Electrotechnical Society，2010，25(2):30－36.

［7］Zheng Z D，Li Y D，Fadel M，et al.A rotor speed and load torque observer for PMSM based on extended Kalman filter［C］//2006 IEEE International Conference on Industrial Technology，Vols 1 －6，Mumbai，2006.

［8］朱元，武四辈，吴志红，等.电动汽车用内置式永磁同步电动机精确转矩控制方法［J］.农业机械学报，2014，45(1):8－13.

ZHU Yuan，WU Sibei，WU Zhihong，et al.Precise torque control method of IPMSM in vehicle［J］.Transactions of the Chinese Society for Agricultural Machinery，2014，45(1):8－13.

［9］Zhang Changfan，Jia Lin，He Jing.Load torque observer based sliding mode control method for permanent magnet synchronous motor［C］//25th Chinese Control and Decision Conference，Guiyang，China，2013:550 －555.

［10］ZHANG Changfan，WANG Yaonan，HE Jing.Variable structure intelligent control for pm synchronous servo motor drive［J］.Proceedings of the CSEE，2002，22(7):13－17.

［11］Zhang Changfan，Huang Yishan，Shao Rui.Robust sensor faults detection for induction motor using observer［J］.Journal of Control Theory and Applications，2012，10(4):528－532.

［12］Zhihong M，Paplinski A P，Wu H R.A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators［J］.IEEE Transactions on Automatic Control，1994，39(12):2464 －2469.

［13］冯勇，鲍晟，余星火.非奇异终端滑模控制系统的设计方法［J］.控制与决策，2002，17(2):194－198.

FENG Yong，BAO Sheng，YU Xinghuo.Design method of non－singular terminal sliding mode control systems［J］.Control and Decision，2002，17(2):194－198.

［14］Feng Y，Yu X H，Man Z H.Non－singular terminal sliding mode control of rigid manipulators［J］.Automatica，2002，38(12):2159 －2167.

［15］Feng Y，Yu X H，Han F L.High－order terminal sliding－mode observer for parameter estimation of a permanent－ magnet synchronous motor［J］.IEEE Transactions on Industrial Electronics，2013，60(10):4272 －4280.

［16］Levant A.Higher－ order sliding modes，differentiation and output－ feedback control［J］.International Journal of Control，2003，76(9－10):924－941.

［17］Boldea I，Paicu M C，Andreescu G D.Active flux concept for motion － sensorless unified AC drives［J］.IEEE Transactions on Power Electronics，2008，23(5):2612－2618.

［18］Boldea I，Paicu M C，Andreescu G D，et al.“Active flux”DTFC － SVM sensorless control of IPMSM［J］.IEEE Transactions on Energy Conversion，2009，24(2):314－322.

［19］周扬忠，毛洁.基于有效磁链概念的永磁同步电动机新型定子磁链滑模观测器［J］.中国电机工程学报，2013，33(12):152－158，198.

ZHOU Yangzhong，MAO Jie.A novel sliding mode stator flux linkage estimator based on active flux principle for permanent magnet synchronous motors［J］.Proceedings of the CSEE，2013，33(12):152 －158，198.

［20］Hasegawa M，Yoshioka S，Matsui K.Position sensorless control of interior permanent magnet synchronous motors using unknown input observer for high－speed drives［J］.IEEE Transactions on Industry Applications，2009，45(3):938－946.

［21］Hasegawa M，Matsui K.Position sensorless control for interior permanent magnet synchronous motor using adaptive flux observer with inductance identification［J］.IET Electric Power Applications，2009，3(3):209 －217.

［22］刘家曦，杨贵杰，李铁才.基于线性磁链的IPMSM位置预估算法［J］.哈尔滨工业大学学报，2011，43(6):81－85.

LIU Jiaxi，YANG Guijie，LI Tiecai.IPMSM rotor position estimation based on linear flux［J］.Journal of Harbin Institute of Technology，2011，43(6):81－85.

［23］Hasan S，Husain I.A luenberger－sliding mode observer for online parameter estimation and adaptation in high－ performance induction motor drives［J］.IEEE Transactions on Industry Applications，2009，45(2):772 －781.