一种匀弹性接触网*

常 丽，李丰良，年晓红

(1.中铁咸阳干部管理学院，陕西咸阳712000;2.中南大学土木工程学院，湖南 长沙410075;3.中南大学信息科学与工程学院，湖南长沙410075)

接触网的工作特点是受电弓在运动中与接触网接触。为了减少离线，要求接触网是匀弹性的。我国著名接触网专家于万聚断言:“当(接触网的)弹性系数在跨距内各点完全一致的条件下，接触线与受电弓的滑板共同以有限的振幅协调地振动着，故不论机车行走速度有多高，均不会产生离线现象［1］。”

但实际的接触网的弹性是不均匀的，德国的接触网弹性及评价标准如表1所示［2］。我国的高速接触网技术主要是引进德高的技术建造的，其弹性不均匀性也存在。实际上接触网的不均匀性是由于接触网本身的悬链型结构决定的，世界各国均是如此。

表1 德国标准接触网的静态特性评价标准Table 1 Catenary statics characteristic and its estimate standard in Germany

为了改善接触网的弹性，不少学者做了大量的工作。钱立新［3］介绍了日本和德国的复链型接触网。图1是日本的复链型接触网的结构图。由于辅助承力索的作用，大大提高了接触网的弹性均匀性，其运营速度达到了250 km/h以上。但是这种接触网由于维护极其困难，没有得到大量推广。张俊杰等［4］为了在分相、中心锚结、定位点等这些接触网的薄弱环节改善接触网的弹性，通过其内部弹簧将这几处导线上的集中负荷卸载为等长度的导线重量。并将负荷传至承力索上。使接触线上各处的单位重量趋于一致。从而使接触网的弹性趋于均匀。但实际上，该方案仍然没有完全消除接触网弹性的不均匀性，也没有得到广泛推广使用。还有的接触网采用弹性吊索，预留驰度等方法改善其弹性，朱飞雄［5］指出，电脑模拟和现场试验表明，Re250型和Re330型接触网的接触线跨中预留弛度不仅无益，反而有害。接触网张力对接触网弹性的均匀性有很大影响［5］。但如何匹配接触线和承力索的张力，找到最佳组合，改善接触网的弹性，汪吉健等［6］作了认真的讨论。但也不能完全消除接触网的弹性的不均匀性。

图1 日本的复链型接触网Fig.1 Complex catenary in Japan

1 关于Mathieu方程

为了探讨接触网弹性对弓网受流的重要影响，我们对弓网关系进行仿真计算。在弓网仿真计算中，目前大都是采用大型有限元软件进行数值分析。数值分析的缺点是不能得到理论解。用数值分析方法讨论某一参数的影响，需要针对这一参数采用不同的值逐一计算。有时，多个参数互相关联，改动一个参数，会影响到其他参数，使用数值计算方法就很难分析。因此，能用理论解讨论弓网问题是最有效的。弓网是一个复杂的系统。不经过简化，要求得理论解几乎是不可能的。但是，如果把弓网系统简化为变弹性系统，可以借用Mathieu方程进行分析，就可以得到理论解。

从电气化铁路出现开始，人们就试图从理论上弄清弓网关系，以便为提高弓网的耦合质量找到解决方案。但弓网是一个复杂的结构，弓网系统动力学又涉及到一个复杂的微分方程组。Mathieu方程就是弓网研究早期使用的一种有代表性的数学模型。这是弓网仿真计算中唯一能用理论解讨论受流特性的方法。

这种模型是把接触网简化成一个变弹性的弹簧、质量系统，如图2所示。在图2中，K1(x)为接触网的弹性刚度;K2为受电弓弓头弹簧刚度 ;M1为接触网的归算质量;M2为受电弓弓头的归算质量;M3为受电弓框架的归算质量;P0为受电弓底座支撑力;yo为受电弓底座的垂向位移。

图2 Mathieu方程使用的弓网模型ig.2 Pantograph and catenary model in the Mathieu equation

接触网的弹性系数K1(x)是一个以跨长为周期的变量，在立柱处最大，在跨中最小，其变化规律可以用余弦函数描述。

式中

称为接触网的平均刚度。L是跨长。

称为弹性不均匀系数。令:

则有:

由图1所示的力学模型可得如下运动微分方程

为了使上式不显含对时间t的导数，做如下变量代换

上式中，v是机车的运行速度，设为常量。将上式代入式(2)得:

令z=πx/L，上式变为

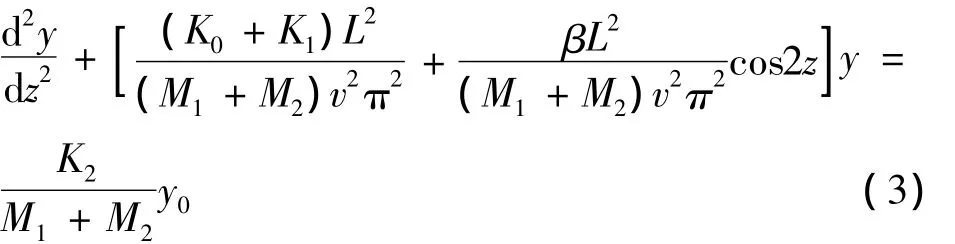
令

将式(4)～(6)代入式(2)～(3)，可以得到:

当yo已知时，式(7)就成了未知函数y的非齐次微分方程。它的解的稳定性取决于相应的齐次方程

这就是著名的Mathieu方程。关于其稳定性的讨论早有结论。图3是Mathieu方程的稳定区域图。图中的阴影部分是不稳定区域，其余是稳定区域。

由式(4)～(5)得

式中为直线方程式(9)的斜率。

图3 Mathieu方程的稳定区域Fig.3 Stability region of Mathieu equation

对于给定的一组弓网参数，代入式(4)和式(5)可求得δ－ε平面上的一个点，若这个点落在不稳定区域内，运动是不稳定的，反之是稳定的。Mathieu方程的稳定区域在δ－ε平面上分布是不均匀的，ε值越小，δ越大，稳定区域越稠密，反之则稀疏。由给定的弓网参数确定的点(δ，ε)又一定在(9)式所确定的直线上。因此也可以说，直线(9)的斜率k越小，则在这条斜率上的点就越容易落在稳定区域，稳定运动的可能性就越大。借助于这一特性，可对弓网的运动稳定性做出如下结论。

1.1 接触网的弹性越均匀，运动稳定性越好，反之越差

接触网的弹性均匀程度取决于β值的大小。由式(10)知，β值越小，接触网弹性越均匀，反之越差。由式(10)知，β值越小，直线(9)式的斜率也就越小。该直线上的点位于稳定区域的可能性也就越大。特别是当β=0时，直线(9)与δ轴重合。注意到直线(9)是一条过坐标原点向右的直线。这说明，只要接触网的弹性是理想均匀的，无论车速如何高，无论弓网的其他参数如何，受流都是稳定的。

1.2 接触网弹性系数和受电弓的弓头弹簧弹性系数越大，受流越稳定

接触网弹性大，K0就越大;受电弓的弹簧系数越大，K2就越大。由(10)式知，直线(9)的斜率就越小，运动就越稳定。增大接触网弹性系数K0的方法是提高接触网的拉力。普通的接触网的总拉力只有2～3 t。高速接触网的拉力明显比这个数值大。法国创记录的574 km/h试验时的接触网拉力达到了5.2 t。可见Mathieu方程的这个结论是正确的。受电弓的弓头弹簧刚度也符合Mathieu方程的规律。高速受电弓通过增加弓头弹簧的刚度的方法也明显提高了受流速度。

1.3 接触网的质量和受电弓弓头的质量(m1+m2)越小，运动稳定性越好

由式(4)和式(5)可知，(m1+m2)越小，δ和ε越大。使直线(9)上的点远离坐标原点O，更容易落在稳定区域，有利于稳定受流。又由于直线(9)的斜率k通常情况下远远小于1，一般来说，δ总是远大于ε。所以，当(m1+m2)变小时，受流稳定区域就会变得更大。接触网的归算质量由承力索和接触线的密度决定。由表2可见，越是高速接触网，其密度越小。受电弓的归算质量也经历了由大到小的变化。我国TSG3受电弓的弓头归算质量是11.4 kg，最高运行速度为120 km/h;DSA200受电弓的弓头归算质量为6.3 kg，最高运行速度可以达到200 km/h以上。

表2 各国接触网的几个主要参数Table 2 A small amount high speed catenary parameters in the wold

结论2要求弹性系数大，结论3要求质量小。弹性系数大意味着要承力索和接触导线的张力大，质量小意味着承力索和接触导线的横截面小。这相当于要求在降低承力索和接触导线横截面的条件下增大抗拉强度。这是个尖锐的矛盾。为了解决这一矛盾，新的高强度材料不断被应用到接触网，大多为优质合金铜材。日本还发明了一种铜包钢的接触线，型号为CS－110，其抗拉强度达到了73.1 kN。最高试验速度达到了425 km/h，试验结果良好。这种接触线既能大幅提高拉力，又可节约成本，值得关注。

1.4 跨长对受流稳定性的影响

由式(4)和式(5)可知，增大跨长L，可以使δ和ε的值增大，使点(δ，ε)落入稳定区域的机会增多。但是增大跨长，会使接触网的不均匀系数增大，从而使直线(9)的斜率k增大，使点(δ，ε)落入不稳定区域的机会增多。由于增减跨长对改善受流有双重影响，所以接触网跨长至今变化不大。

由Mathieu方程所得出的上述判断无疑是正确的。这些判断，在高速电气化铁路的发展过程完全得到了证明。对于指导弓网的设计起到了巨大的作用。

以上是根据Mathieu方程讨论得出的几个判断。无数事实证明了这些判断的正确性，至今仍指导着弓网研究的方向。但是，Mathieu方程毕竟把弓网系统简化得太多，只能用它得到几个方向性结论，不能用做定量讨论，有时甚至会遇到一些难以解释的问题。例如，受电弓的归算质量越小越好，但是，仅靠降低归算质量还不行，还需要从结构上加以改进。如今的受电弓滑板由直线型改为了曲线形;受电弓的滑板间距也有越来越大的趋势，这些都是Mathieu方程不能解释的。出现这些问题，都是由于Mathieu方程使用的弓网力学模型过于简单的缘故。

2 一种匀弹性接触网

Mathieu方程只要能建造一种弹性均匀的接触网，就能使受流速度在理论上无限提高。现有接触网弹性不均匀的根本原因是由于接触线和承力索都是柔软的，在立柱处将它们悬挂起来。这种结构在力学上称为悬链型结构。这种结构的特点是其垂向弹性以跨长为周期变化。由于接触网的弹性不均匀，使得受电弓在运动过程中时而上升，时而下降。受电弓运行速度比较慢时，受电弓能够调整自己的姿态，跟随接触网一起运动。当受电弓高速运行时，弓网波动加快，幅度增加，受电弓不能跟随接触网一起振动，就产生了离线。

如前所述，现有接触网不可能做到张力无限大，质量无限小，因此，在现有的接触网上彻底解决接触网的不均匀性问题是不可能的。既然造成弹性不均匀的根源是接触网的链型悬挂造成的，要解决这个问题，可以采用图4所示的结构。

图4 一种匀弹性接触网Fig.4 A catenary with equal elasticity

在图4中，接触网没有承力索，取而代之的是一个桁架结构。这个桁架固定在立柱上，刚度足够大，可以看作刚体，且与轨面平行。接触线通过吊弦平直地悬挂在桁架的下方。由于桁架可以看作刚性结构，接触线可以认为是通过吊弦与固定物体连接。这从根本上改变了接触网链型悬挂的动态特性，形成了一种所谓的匀弹性接触网。由于这种接触网的是顶部为刚性结构，不妨取名为刚顶架匀弹性接触网。

由于刚顶架匀弹性接触网的顶部是刚性的，定位器就没有必要安装在支柱旁。图4就是把定位器安装在跨中。

3 结论

(1)匀弹性接触网理论上无速度上限。由于接触网的弹性是均匀的，彻底消除了由于接触网变弹性产生的波动，相当于为受电弓修建了一条平直的高速公路，接触网的动态特性不再成为限制受流速度的主要因素。

(2)成本不高。顶部的桁架没有什么附加载荷，可以使用普通材料建造。接触导线也不再需要像链型悬挂接触网那样靠提高张力来改善弹性，因此也降低了接触导线对材质要求。综合这些因素，估计这种接触网不会明显增大接触网的造价。

(3)容易维护。日本和德国的复链式接触网由于采用了大量的柔性物体，其几何形状容易受外界因素影响而改变，很难维护。刚顶架匀弹性接触网大大减少了网上的柔性物体，为减少日常维护工作量打下了良好的基础。

［1］于万聚.高速电气化铁路接触网［M］.成都:西南交通大学出版社，2003.

YU Wanju.High Speed Electric Railway Catenary［M］.Chengdu:SouthwestTransportation UniversityPress，2003.

［2］朱飞雄.接触网弹性链形悬挂的弓网关系检测［J］.电气化铁道，2003，14(1):15 －17.

ZHU Feixiong.Examine the relationship of the elastic catenary and pantograph［J］.Electric Railway，2003，14(1):15－17.

［3］钱立新.世界高速铁路技术［M］.北京:中国铁道出版社，2002.

QIAN Lixin.High speed railway technology in the world［M］.Beijing:Railway Press of China，2002.

［4］张俊杰，薛芳群.均匀接触网弹性及改善弓网取流质量的探讨［J］.电气化铁道，2001，12(3):24 －25.

ZHANG Junjie，XUE Fangqun.Improve the catenary elasticity and current feed［J］.Electric Railway，2001，12(3):24－25.

［5］朱飞雄.接触网弹性链形悬挂的设计、施工与检测要点［J］.铁道标准设计，2008，42(1):85 －87.

ZHU Feixiong.Design，construct and examine the elastic part of the catenary［J］.Railway Standard Design，2008，42(1):85－87.

［6］汪吉健，田志军，李会杰，等.承力索张力对弓网受流质量影响研究［J］.铁道学报，2005，27(1):114 －118.

WANG jijian，TIAN Zhijun，LI Hujie，et al.Study of the influence current－receiving quality between pantograph and OCS from tensile force acting on catenary wire［J］.Journal of the China Railway Society，2005，27(1):114－118.