基于正交距离最短的平面线形拟合方法及应用*

王利朋，刘成龙，杨雪峰

(西南交通大学地球科学与环境工程学院，四川成都611756)

随着我国高速铁路的发展以及普速铁路的提速，铁路轨道的平顺性评价以及轨道不平顺处的调整逐渐成为一个非常重要的研究课题。轨道不平顺不仅限制列车运行的速度，还直接影响列车运行的平稳性。当线路设计文件缺失或现有的线路设计文件不再具有现实性时，就需要通过线形拟合确定一个与既有线路实际情况最为契合的线形，这一工作称为轨道线形整正优化，传统上这个过程中采用的基本准则为最小二乘准则。利用最小二乘原理可以简便地求出既有线直线段与圆曲线段拟合模型中的未知参数，即直线的斜率和截距、圆曲线的圆心和半径，并且使得残差平方和最小。传统的最小二乘拟合方法只考虑线路平面坐标观测值(x，y)中单一变量x或y的测量误差，实际测量过程中坐标x与y均有误差［1－3］，而依据正交距离最短的原则进行既有线线形的拟合，就是同时考虑x与y均有误差。本文依据正交距离最短的原则进行铁路既有线线形的拟合，并将它与传统的的最小二乘拟合方法进行对比。通过实例计算和精度评定，证明了基于正交距离最短的最小二乘线形拟合效果要优于传统的最小二乘线形拟合，前者可以得出与轨道线形最为契合的函数模型。正交距离最小二乘线形拟合按照拨道量的平方和最小这一准则确定法方程并求解模型参数，不仅简化了参数求解过程，提高了线形拟合的整体精度，而且获得了更小的圆度。

1 正交距离最短的线形拟合原理

1.1 正交距离最短的直线拟合原理

设欲拟合的直线方程为:

式(1)中a和b分别为直线的截距和斜率，设a0和b0为a和b的近似值，δa和δb为a0、b0的改正数，于是有:

任一平面测点(xi，yi)到拟合直线距离的平方为:

即正交距离最短的直线拟合误差方程的矩阵形式为:

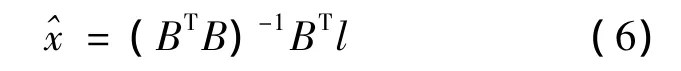
则未知参数的方差－协方差阵为:

1.2 正交距离最短的圆曲线拟合原理

设欲拟合的圆曲线方程为:

把式(6)的结果代入式(5)后，可按下式计算验后单位权方差为:X0，Y0和 R0分别为和的近似值，δx，δy和 δr为圆曲线方程中参数的改正数，则:

任一平面测点(Xi，Yi)到拟合圆的距离为:

将式(11)在(X0，Y0，R0)处按照多元函数的泰勒级数展开式进行展开，并略去二次项和更高次项后得到线性化的距离误差方程纯量形式为:

上述距离矩阵形式的误差方程为:

设Si等精度，按照最小二乘准则求解，得到圆曲线参数改正数的平差值:

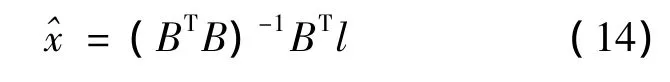
之后，可按照式(7)和式(8)类似的原理，计算圆曲线拟合后的验后单位权方差和未知参数的方差－协方差阵。

2 正交距离最短与普通最小二乘法线形拟合的比较与分析

为了比较正交距离最短最小二乘与普通最小二乘的线形拟合效果差异情况，采用某普速铁路上一段直线数据与一段圆曲线数据进行计算实验，然后通过比较不同拟合方法计算得出的参数估值的精度、样本点的残差以及验后单位权中误差，分析不同拟合方法的拟合效果。由于轨道线形测量数据量庞大，在此仅列出利用直线段10个样本点进行拟合的对比结果和利用圆曲线段18个样本点进行拟合的对比结果。直线段样本点坐标如表1所示，2种方法拟合的残差如表2所示，参数估值及精度信息如表3所示。圆曲线段样本点坐标如表4所示，残差对比如表5所示，圆曲线拟合的参数估值及精度信息如表6所示。

表1 直线段线形拟合样本点Table 1 Sample points of line－fitting

表2 直线段不同拟合方法计算的残差Table 2 Residual errors of different line－fitting methods

表3 直线段不同拟合方法计算的参数估值及精度信息Table 3 Parametric estimation and precision of different line－fitting methods

为了更准确地描述轨道线形实测点与拟合线形的接近程度，引入圆度作为一个评价标准。圆度是指圆柱体截面上一个实际圆与理论圆(本文中理论圆为拟合圆)的接近程度，为最大外接圆半径与最小内接圆半径之差值［4］。引入到线形拟合中，可以表示为线形实测点到拟合线形的最大与最小距离之差，也可以表示为所有样本点的最大与最小残差的差值，此时，表2中的“+”、“－”作为数学意义上的正负参与运算。该指标表示实际线形相对于拟合线形的波动范围，在轨道调整中可以代表拨道量的区间。

从表2可以看出，正交距离最小二乘法的残差更加均匀，其圆度为e1=1.39 mm，即轨道调整时拨道量区间较小;而普通最小二乘法的残差分布不均匀，其圆度为e2=3.86 mm，拨道量区间相对较大，不利于轨道的调整。从验后的精度信息来看，表3中数据表明正交距离最小二乘法解算的参数精度高于普通最小二乘法，说明这种方法得到的线形更加符合实际情况。

表4 圆曲线段曲线拟合样本点Table 4 Sample points of circular curve－fitting

表5 圆曲线段不同拟合方法计算的残差Table 5 Residual errors of different circular curve－fitting methods

表6 圆曲线段不同拟合方法计算的参数估值及精度信息Table 6 Parametric estimation and precision of different circular curve－fitting methods

如表5所示，正交距离最小二乘法计算得出的残差总体上要小于普通最小二乘法且更加均匀，表6数据表明正交距离最小二乘法的验后单位权中误差要优于普通最小二乘法，2种方法的参数精度几乎相等。正交最小二乘法的圆度为e3=4.5 mm，而普通最小二乘法的圆度为e4=10.3 mm，即2种方法的轨道调整量相差5.8 mm，因此，在进行圆曲线拟合时，正交最小二乘法要优于普通最小二乘法。出于工程量和工作效率的考虑，理应以正交距离最小二乘法取代普通最小二乘法作为线形拟合的最优方法，并以此为依据计算拨道量。

3 结论

(1)从前面所述的2种拟合方法的拟合原理可以看出，基于正交距离最短的最小二乘法同时考虑了样本点在x和y 2个方向上的误差，而普通最小二乘法仅考虑了一个方向上的误差。因此，按照正交最小二乘法所开列的误差方程要优于普通最小二乘法。

(2)通过实测数据的拟合结果可以看到，正交距离最小二乘法的残差总体上小于普通最小二乘法的残差。而且前者的圆度小于后者，这一点对于既有线的整正优化具有重要意义，因为圆度的大小直接决定了轨道调整量的区间，这也说明了正交距离最小二乘法有利于减少工作量，从而提高工作效率。

(3)采用本文提供的算法，直线拟合中验后精度提高了2～3倍，轨道调整量区间减小了2.47 mm;圆曲线拟合中验后精度几乎相等，轨道调整量区间减小了5.80 mm。因此，在线形拟合和轨道调整工作中应采用正交距离最小二乘法取代普通最小二乘法是具有实际意义的。

［1］丁克良，欧吉坤，赵春梅.正交最小二乘曲线拟合法［J］.测绘科学，2007，32(3):18－19.

DING Keliang，OU Jikun，ZHAO Chunmei.Method of orthogonal least squares in curve － fitting［J］.Science of Surveying and Mapping，2007，32(3):18 －19.

［2］朱文华，覃爱丽.基于几何距离准则拟合铁路线路参数的研究［J］.铁路计算机应用，2010(5):14－16.

ZHU Wenhua，QIN Aili.Study on track parameters based on geometry distance［J］.Railway Computer Application，2010(5):14－16.

［3］丁克良，沈云中，欧吉坤.整体最小二乘法直线拟合［J］.辽宁工程技术大学学报(自然科学版)，2010(1):44－47.

DING Keliang，SHEN Yunzhong，OU Jikun.Total least squares on linear fitting［J］.Journal of Liaoning Technical University(Natural Science Edition)，2010(1):44 －47.

［4］丁玲.圆度与圆柱度误差评定算法的设计与应用［D］.西安:西安电子科技大学，2013.

DING Ling.The design an application of roundness and estimative Methods［D］.Xi’an:Xidian University，2013.

［5］曾接贤，张桂梅，储珺，等.霍夫变换与最小二乘法相结合的直线拟合［J］.南昌航空工业学院学报 (自然科学版)，2003，17(4):9－13.

ZENG Jiexian，ZHANG Guimei，CHU Jun，et al.Combination of hough transformation and least squares on linear fitting［J］.Journal of Nanchang Hangkong University(Natural Sciences)，2003，17(4):9 －13.

［6］雷宜武，肖萍.直线拟合的一个快速算法［J］.华中理工大学学报，1994，22(1):75－78.

LEI Yiwu，XIAO Ping.A fast method of linear fitting［J］.Journal of Huazhong University of Science and Technology，1994，22(1):75－78.

［7］兰燕娜，薛同莲，李雅丽，等.基于VB语言实现最小二乘法直线拟合［J］.长江大学学报(自然科学版)，2011，8(6):92－94.

LAN Yanna，XUE Tonglian，LI Yali，et al.Achievement of least squares on linear fitting based on VB［J］.Journal of Yangtze University(Natural Science Edition)，2011，8(6):92－94.

［8］乔立山，王玉兰，曾锦光.实验数据处理中曲线拟合方法探讨［J］.成都理工大学学报(自然科学版)，2004，31(1):91－95.

QIAO Lishan，WANG Yulan，ZENG Jinguang.Methods of curve － fitting in experimental data［J］.Journal of Chengdu University of Technology(Science＆Technology Edition)，2004，31(1):91－95.

［9］许恺.三种曲线拟合方法的精度分析［J］.上海铁道大学学报，1996，17(3):26－30.

XU Kai.Precision analysis of three different curve － fitting methods［J］.Journal of Shanghai Tiedao University，1996，17(3):26－30.

［10］陈峰，辜良瑶，杨岳，等.铁路既有线复测平面曲线优化方法［J］.铁道科学与工程学报，2012，9(5):90－95.

CHEN Feng，GU Liangyao，YANG Yue，et al.Optimum method for horizontal curve re－surveying of the existing railway［J］.Journal of Railway Science and Engineering，2012，9(5):90－95.

［11］於宗俦，陶本藻，刘大杰.广义测量平差［M］.北京:测绘出版社，1992.

YU Zongchou，TAO Benzao，LIU Dajie.Generalized surveying adjustment［M］.Beijing:The Publishing House of Surveying and Mapping，1992.

［12］宋力杰.测量平差程序设计［M］.北京:国防工业出版社，2009.

SONG Lijie.Program design of survey adjustment［M］.Beijing:National Defence Industry Press，2009.

［13］徐士良.数值分析与算法［M］.北京:机械工业出版社，2003.

XU Shiliang.Numerical analysis and algorithm［M］.Beijing:Machinery Industry Press，2003.

［14］Hough P V C.Method and means for recognizing complex patterns:U.S.Patent 3，069，654［P］.1962 －12 －18.

［15］Lancaster P，Salkauskas K.Surfaces generated by moving least squares methods［J］.Mathematics of Computation，1981，37(155):141－158.

［16］Belytschko T，Lu Y Y，Gu L.Element‐free Galerkin methods［J］.International Journal for Numerical Methods in Engineering，1994，37(2):229 －256.