基于改进差分算法的高速列车运行调整研究＊

曹岩，孟学雷

（1.兰州交通大学 电子与信息工程学院，甘肃 兰州730070；2.兰州交通大学 交通运输学院，甘肃 兰州730070）

铁路区段内列车运行计划的制定与调整是铁路行车调度指挥工作中的核心，决定着区段内行车组织工作的质量。因此，铁路行调指挥的自动化是近年来研究的热点。随着我国高速铁路网络的不断完善，我国铁路发展进入了一个崭新的历史时期，在新形势下如何确定高速列车运行调整方案，既满足乘客与货主的运输需求，又提高线路车站的使用效率，是一个亟待解决的问题。目前，许多计算模型和智能算法逐步被应用到解决列车运行计划制定与调整问题的研究上来。对于列车运行调整问题相关学者展开了诸多研究。Cacchiani等［1］建立了列车铺画的线性规划模型，以最多的列车数量为运行图该模型的优化目标。Meng等［2］建立了以总晚点时间最少为目标的非线性列车运行调整模型并设计了一种新的粒子群算法进行求解。Castillo等［3］以总的旅行时间最少建立了列车运行调整模型并设计了两段法策略进行求解。Min等［4］针对列车运行冲突的消解是NP－hard问题，设计了基于column－generation的列车运行调整算法。Almodovar等［5］基于离散事件仿真模型建立了一种实时的列车运行调整系统，并设计了贪婪算法进行求解。Lamorgese等［6］设计了一种列车运行调整的分解算法。Albrecht等［7］设计了“问题空间搜索”方法求解列车运行调整问题。Wang等［8］设计了高速铁路运行调整的双层规划模型。黄鉴等［9］建立了以列车总旅行时间、运行图均衡性目标一级区间服务频率偏差为目标的列车运行图优化模型，并设计模拟退火优化算法求解。近年来，差分算法以其优秀的算法性能得到了关注，也应用到了列车运行调整及控制问题的求解中。韩蕙心等［10］利用差分算法求解其建立的基于多目标的列车运行控制问题。严细辉等［11］建立了高速列车运行操纵多目标优化模型并利用差分算法进行求解。本文在研究经典种群算法的基础上，引入多策略的种群寻址模式和多子群协同进化机制，并将改进的算法应用于高速列车运行调整模型的求解中，得到了一种高速列车运行调整新的解决方法。

1 高速铁路运行调整模型

当列车运行受到干扰，产生列车晚点时，通过适当地调整列车的运行计划，即改变各列车在车站的到、停时分及在区间的运行时间，使列车的运行最终回到计划运行图上，是列车运行调整的目的。高速铁路列车运行调整是一项十分复杂的工作，其直接关系到铁路行车安全，所以高速铁路列车运行调整问题亟待研究。一般地，高速铁路列车运行状况调整的主要措施有：

（1）增加列车的停车站。

（2）延长列车在停车站的停车时分。

（3）选择合理的会让站、越行站，加速放行列车。

（4）组织列车进行快速、平行作业，缩短列车在站作业时间。

（5）充分利用列车运行的最大允许速度，缩短列车区间运行时分。

（6）其他方法：如组织反方向行车，组织列车合并运行等。

这些措施的实施最终体现在对高速列车到站／离站及通过车站的调整。

设研究的区段内共有N列车，M个车站，所谓车计划就是指某列车在区段内从始站到终站的各站的到发时分及作业性质。则列车i在车站k的计划为1个三元组［12］。可以描述为：

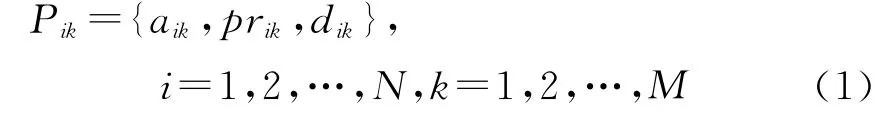
其中aik，dik分别为列车i的到达时分和发车时分，PRik表明列车i在车站k的预定作业类型，

那么，实际运行状况可以由各列车经过各站的到发时分来表征，因而可以由N×M个点计划来描述［12］，即

由于Pik是1个三元组，于是OG可以分解成为到达矩阵GA，出发矩阵GD和作业标志矩阵PR：

既定运行图的列车到达时分矩阵。

又令SL＝ ｛slk｝（k＝1，2，…，M），表示车站k的到发线的数量，TO＝ ｛toik｝（k＝1，2，…，M）表示列车i在站k的技术作业时间。进入调整的每一列车都有一个最早接入时间hk，最早发车时间fk和最晚开出区段或到达终点的时间gk，对应列车在指定时间段［hk，gk］内，应该结束在本调度区段内的运行。

那么，根据以上约定，以总晚点时间最少的列车运行调整问题的数学模型如下：目标函数

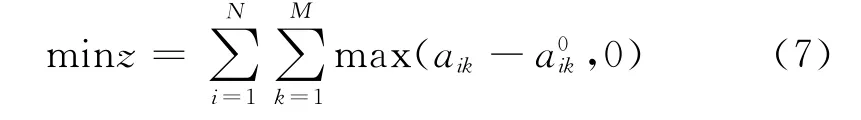
满足约束

式（8）表示列车i在站k的停车时间必须大于等于技术作业所需的时间；

式（9）表示追踪列车占用区间的开始时刻晚于前行列车占用同一区间的结束时刻；

式（10）列车运行的区间顺序约束，表明列车必须按时间顺序依次通过各个区间，I为追踪列车间隔时间；

式（11）表示同一列车开始占用到发线的开始时刻早于结束时刻；

式（12）表示所有列车的发车时刻晚于最早发车时间；

式（13）表示所有列车占用某区间的开始时间晚于最早接入时间；

式（14）为车站到发线能力约束，即该方向某种列车数和列车总数不能超过相应的车站线路数；式中N（aik＋t停≤dik）表示已到达车站k但并没有离开车站k的列车数；

式（15）～（16）表示不能办理同时接发同方向列车的车站，两车间隔应满足不同时发到间隔时间τ发到和不同时到发间隔时间τ到发。

2 差分进化算法及其改进策略

2.1 基本差分进化算法

差分进化算法（DE）是一种用于优化问题的启发式算法。本质上说，它是一种基于实数编码的具有保优思想的贪婪遗传算法 。同遗传算法一样，差分进化算法包含变异和交叉操作，但同时相较于遗传算法的选择操作，差分进化算法采用一对一的淘汰机制来更新种群。由于差分进化算法在连续域优化问题的优势已获得广泛应用，并引发进化算法研究领域的热潮。差分进化算法由Storm以及Price提出，算法的原理采用对个体进行方向扰动，以达到对个体的函数值进行下降的目的，同其他进化算法一样，差分进化算法不利用函数的梯度信息，因此对函数的可导性甚至连续性没有要求，适用性很强。同时，算法与种群优化有相通之处，但因为差分进化算法在一定程度上考虑了多变量间的相关性，因此相较于种群优化在变量耦合问题上有很大的优势。

基本差分算法的步骤是：

（1）初始化种群。随机产生L个染色体，其中，每一个染色体由P个基因构成。初始种群xi（0），i＝1，2，…，L，其中，xi（0）由P个基因构成，为xi1（0），xi2（0），…，xiP（0）。

（2）变异。利用差分策略对染色体的基因进行变异。差分策略有多种，常用的一种是随机选取种群中2个染色体，然后求出两者的向量差，乘以缩放因子得到一个新的向量，将该向量与待变异的向量相加，得到新的染色体。

其中，λ为缩放因子。xi（k）表示第k代种群中第i个个体。

（3）交叉。以一定的概率进行交叉操作。为了保证变异中间染色体的基因传给下一代，强制要求将变异中间染色体的一个基因抽取并植入下一代的染色体中。

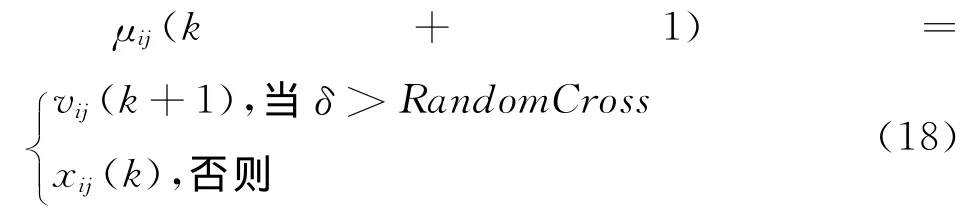
其中，RandomCross是介于0与1之间的一个随机数。

（4）选择。差分算法采用贪婪算法选择进入下一代种群的个体。

2.2 基于三角形差分策略的差分进化算法

不难发现，基本差分算法的差分策略较简单，其优点是在设计算法时易于实现，算法速度又能得到保证。但是，过于简单的差分策略带来的风险是染色体的变异特征不能充分在子代中体现，可能会导致求解结果早熟，陷于局部最优。所以，本文设计了一种新的差分策略，充分考虑不同变异染色体的特征，使染色体更优。

本策略中，在本代染色体中，随机选择包含已经变异的染色体xr1（g），xr2（g），xr3（g），运用这3条染色体，产生新一代染色体。新一代染色体的计算公式为：

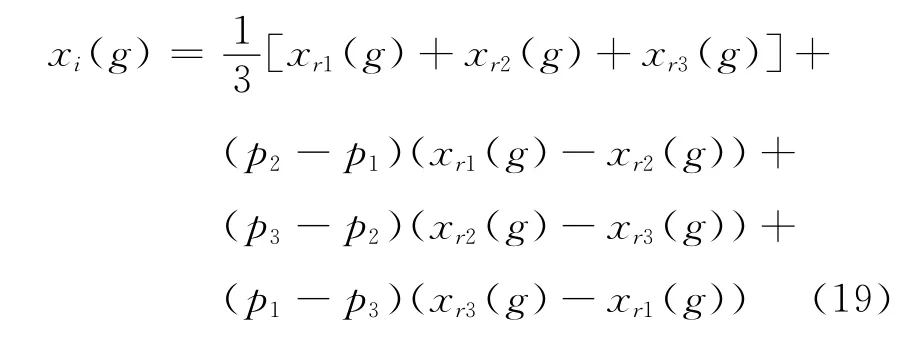
其中，

可见，新一代染色体的规则充分考虑了上一代染色体的特征，避免了列车运行调整计算时出现早熟从而影响列车运行调整方案质量的现象。

2.3 针对高速铁路运行调整模型的差分算法设计

2.3.1 种群规模的设计

设计种群的规模，以较为恰当的种群规模进行计算。针对列车运行调整问题，设计种群的规模介于20～50之间，在保证高速列车运行调整迭代计算的速度基础上，防止运行调整的计算结果陷入局部最优。

2.3.2 染色体设计

列车的数量为N，其经过的车站数量为M，那么径路上存在M－1个区间。因为某列车在每个车站的到达时刻和出发时刻对应2个决策变量，那么，决策变量的数量是2×N×M个。每一个变量代表一个时刻。又因为全天24h是1 440 min，所以将染色体视为一个用二进制表示的数字，数字的大小表示该时刻与0∶00之间的分钟数。如8∶30距离0∶00有510min，则表示为0001 1111 1110。

2.3.3 计算停止条件

在高速列车运行调整计算中，迭代计算停止的条件设计有2种。一种通过设定种群算法的迭代次数上限控制循环次数。另一种通过控制计算结果与目标结果之间的差距控制循环次数。本文采用第2种方法，设计相当简便，当迭代次数设置较合理时，能够得到较理想的计算结果。

2.3.4 计算步骤

设计针对列车运行调整的计算步骤为：

第1步：设置计算结果与目标结果之间的允许差值；

第2步：初始化种群。设置粒子种群的规模是Ngen。每一粒子的位置向量由2×N×M×Ngen个变量构成。根据列车晚点情况，设置每一个变量的初始值；

第3步：计算适应度函数的值Z。将各粒子的最优位置进行记录，并记录使得适应度函数的值最小的染色体；

第4步：变异，交叉，选择：根据上述设计的变异、交叉、选择规则进行染色体变异、交叉、选择；

第5步：计算适应度值，并求得计算结果与目标结果之间的差值，若小于等于第1步设置的允许差值，则根据种群中最优粒子的最优位置，给出高速列车运行调整后各列车在车站的到达和出发时刻；否则，转第3步。

3 计算实例与分析

选取京广高速铁路广州南至衡阳东的上行列车运行数据作为实验数据。如表1所示，在8∶00～11∶00之间，京广铁路的上行方向，有 G280，G1108，G832，G1002，G1110，G6102，G276，D7802，G1112，G1004，G6104，G542，G1006，G532及G822共15个车次的列车在该区段上运行。其具体的列车运行时刻见表1。

表1 京广高速铁路广州南至衡阳东8∶00至11∶00原列车时刻表Table 1 The original timetable between Guangzhounan and Hengyangdong of Beijing－Guangzhou high speed railway from 8∶00to 11∶00

假设某日由于铁路设备故障，使得部分高速列车出现晚点，即G1108到达郴州西时晚点10 min、G1002到达韶关时晚点13min，G1112，G6104，G542，G1006到达广州北时晚点10min。可见，初始总晚点时间已经达到了63min，考虑列车晚点传播的影响，根据上述设置的求解步骤，首先设置目标总晚点值控制在150min内，而允许的计算结果与目标结果之间的允许差值为5min，即计算结果的值在155min以内，就结束循环计算。

根据上述设计的求解步骤，设计粒子群的规模为20，那么位置向量由2×15×8×20＝4 800个变量构成。

根据上述设计的列车运行调整的改进的差分算法，计算得到结果。然后将计算结果还原为如表2所示的新的列车时刻表。调整后的列车运行图如图1所示。

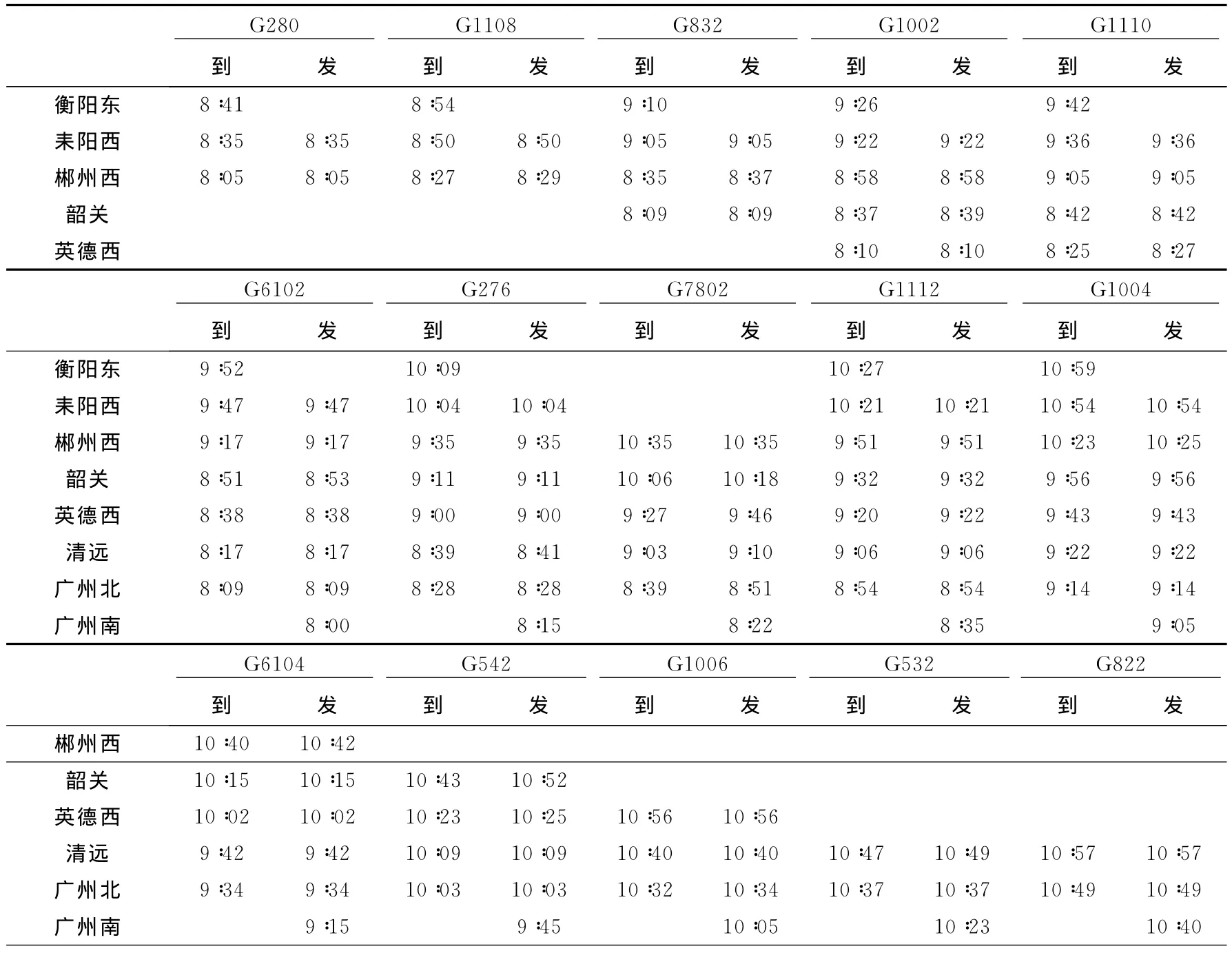
表2 京广高速铁路广州南至衡阳东8∶00～11∶00调整后列车时刻表Table 2 Rescheduled timetable between Guangzhounan and Hengyangdong of Beijing－Guangzhou high speed railway from 8∶00to 11∶00

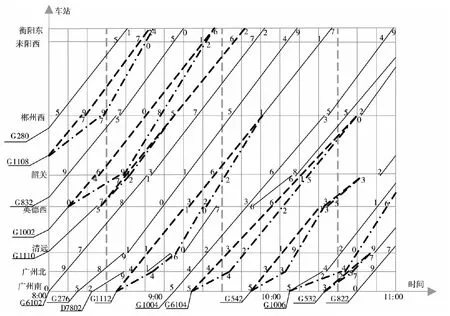
图1 京广高速铁路广州南至衡阳东8∶00～11∶00调整后列车运行图Fig.1 Rescheduled operation chart between Guangzhounan and Hengyangdong of Beijing－Guangzhou high speed railway from 8∶00to 11∶00

图1中，虚线为原列车运行计划线，但是由于设备故障不能兑现。点画线为新调整后的列车运行线。从图1及表2中的数据可知，本文设计的方法可以得到合理可行的列车运行计划。最后求得的适应度值即总晚点时间为153min，小于目标值155min，与目标值150min只差3min，达到了算法中对于计算精度的要求。

具体而言，G1108由于在郴州西站晚点，在郴州西至耒阳西及耒阳西至衡阳东2个区间赶点，但由于区间最小运行时分的限制，列车在到达衡阳东时仍然晚点2min。G1002晚点13min，而要保证在韶关停站2min，8：39才能从韶关站出发。此时，若考虑G1110不晚点通过韶关站，又要满足列车之间的追踪间隔，势必造成G1002在韶关站被G1110越行，由于等级相同，G1002不能越行G1110，所以最后将造成G1002严重晚点，所以，此时采取的策略是将G1110到达韶关站的时间推迟2min，G1002仍然运行在G1110前方，并进行赶点，使其在郴州西恢复按图运行。G1006与G532之间的情况同理。G1112和G6104赶点，在郴州西恢复按图运行，G542在韶关恢复按图运行。可见，本文设计的模型和算法，在考虑列车运行约束的基础上，使得列车运行调整的方案更合理。

4 结论

（1）建立的高速铁路运行调整模型较完整地描述了高速列车行调工作问题。模型考虑高速列车停站时间、追踪间隔时间、到发线数量约束、高速列出的接入调整区段时间、不同时到发间隔时间与不同时发到间隔时间等约束，为得到合理的高速铁路列车运行调整方案奠定了基础。

（2）设计的基于三角差分策略的高速铁路列车运行调整差分算法适合求解本文所建立的列车运行调整模型，由计算结果还原而成的列车运行计划合理。

（3）所提出的高速铁路列车运行的模型和算法是切实可行的，可为我国新一代的铁路列车运行调度系统建设提供一种可借鉴的建模与算法方案。

［1］Cacchiani V，Caprara A，Toth P.Scheduling extra feight trains on railway networks［J］.Transportation Research Part B，2010，44（2）：215－231.

［2］Meng X L，Jia L M，Qin Y.Train timetable optimizing and rescheduling based on improved particle swarm algorithm［J］，Transportation Research Record，2010，2197：71－79.

［3］Castillo E，Gallego I，Urena J M，et al.Timetabling optimization of a mixed double－and single－tracked railway network［J］.Applied Mathematical Modelling，2011，35（2）：859－878.

［4］Min Y H，Park M J，Hong S P，et al.An appraisal of a column－generation－based algorithm for centralized train－conflict resolution on a metropolitan railway network［J］.Transportation Research Part B，2011，45（2）：409－429.

［5］Almodóvar M，García－Ródenas R.On－line reschedule optimization for passenger railways in case of emergencies［J］.Computers ＆ Operations Research ，2013，40（3）：725－736.

［6］Lamorgese L，Mannino C.The track formulation for the train dispatching problem［J］.Electronic Notes in Discrete Mathematics，2013，41：559－566.

［7］Albrecht A R，Panton D M，Lee D H.Rescheduling rail networks with maintenance disruptions using problem space search［J］.Computers ＆ Operations Research，2013，40（3）：703－712.

［8］Wang L，Mo W T，Qin Y，et al.Optimization based high－speed railway train rescheduling with speed restriction［J］.Discrete Dynamics in Nature and Society，2014，Article ID 934369，http：／／dx.doi.org／10.1155／2014／934369.

［9］黄鉴，彭其渊.基于分时客运需求的客运专线列车运行图优化［J］.铁道科学与工程学报，2012，9（6）：66－71.

HUANG Jian，PENG Qiyuan.Train diagram optimization of passenger dedicated line based on passenger transport demand in different time［J］.Journal of Railway Science and Engineering，2012，9（6）：66－71.

［10］韩蕙心，吴鹏，吴杰，等.基于多目标差分进化算法的列车惰行控制［J］.计算机应用，2013，33（A02）：286－289.

HAN Huixin，WU Peng，WU Jie，et al.Coast control of urban train based on multi－objective differential evolution algorithm［J］.Journal of Computer Applications，2013，33（A02）：286－289.

［11］严细辉，蔡伯根，宁滨，等.基于差分进化的高速列车运行操纵的多目标优化研究［J］.铁道学报，2013，35（9）：65－71.

YAN Xihui，CAI Bogen，NING Bin，et al.Research on multi－objective high－speed train operation optimization based on differential evolution［J］.Journal of the China railway Society，2013，35（9）：65－71.

［12］贾利民.模糊控制与决策及其在铁路自动化中的应用［D］.北京：中国铁道科学研究院，1991：107－113.

JIA Limin.Fuzzy control and deciding and its application in railway automatization［D］.Beijing：China Academy of Railway Sciences，1991：107－113.