绳正法在高铁曲线整道的适用性分析＊

魏晖，朱洪涛，殷华，3，蔡军，戚志刚

（1.南昌大学 机电工程学院，江西 南昌330031；2.江西科技学院 汽车工程学院，江西 南昌330098；3.江西农业大学 软件学院，江西 南昌330045；4.兰州铁路局 工务处，甘肃 兰州730000）

轨道在重复性的载荷作用下，将产生残余变形，进而轨道质量劣化，影响行车的安全及乘车的舒适。要保证轨道质量的均衡，需要通过日常的轨道整理以校正轨道的残余变形。而残余变形的校正，涉及到不平顺的测量与整道量的计算问题。关于轨道平顺性测量，目前的测量手段有动态测量与静态测量；而整道量计算的方法，又可以分为基于外部几何尺寸的坐标法以及基于内部几何尺寸的渐伸线法2类。渐伸线方法又包含矢距法、偏角法与绳正法3种方法。由于绳正法操作较简便，因此绳正法广泛应用于普速线路以及提速线路的整道计算。由于方法中隐含整正前后的曲线转角（α）和线路长度（L）均不变的假设，且采用有限点的累和替代积分运算，因而渐伸线法的拨正是有条件的。黎浩廉［1］从分析曲率半径控制的角度出发，认为渐伸线类方法适用条件应为：对于无缝线路转角不宜大于1rad，对于有缝线路也不宜超过2.1rad；郝瀛［2］则从既有线改建的拨距控制角度分析渐伸线方法的适用性，认为当QZ点拨距误差≤0.05m时绳正法等渐伸线方法适用；刘永孝等［3］则从坐标法与渐伸线法的拨距对比角度分析2类方法的拨距与正矢的差异，认为渐伸线法计算的拨距误差和拨后正矢误差都与偏角的大小有关，但其计算精度可以满足曲线整正基本要求。以上成果对于普速及提速线路的曲线养护提供了理论依据，然而上述研究并未对渐伸线方法在高速铁路曲线养护中的适用性进行讨论；另外，已有研究常以级数分解为分析工具并通过算例进行说明渐伸线方法的适用性；还有，计算中对于拨正质量即拨后的平顺性也少有涉及。本文以绳正法为例，采用向量方程来分析渐开线法的性状与精度，并讨论其在高铁曲线养护中的适用性。

1 绳正法原理与操作

绳正法利用曲线上正矢与曲率之间的关系，改正正矢，使之恢复原有的设计曲率，并通过相应的拨量，把它拨正到原来的设计位置［4－5］。一般操作常采用外股轨道为基准线，按等间距l（如10m）对曲线设桩，计测桩号为i（i＝0，1，2，…，n，n＋1）；然后用长为2l（如20m）的弦线，两端紧贴相邻桩点处外轨踏面下16mm作用边并张紧，测取中间桩点的弦矢高，得到实测正矢序列｛fi｜i＝1，2，…，n｝；依据设计参数，可计算设计正矢序列｛Fi｜i＝1，2，…，n｝。关于绳正法拨量计算，可采用简易法或流水法［6］。无论是简易法抑或是流水法，均基于渐伸线原理，只是计算格式有所区别。原理如下：

假定轨道任一点均沿渐伸线移动且移动前后轨道长度不变，并令正矢差

则拨量ei：

在车上的我，好像飞行在一个醒觉之后就要忘记了的梦里。我似乎有一桩事情没有做完成，我心里有着一种牵挂。但这并不曾很清晰地意识着。我几次想把手中的伞张起来，可是随即会自己失笑这是无意识的。并没有雨降下来，完全地晴了，而天空中也稀疏地有了几颗星。

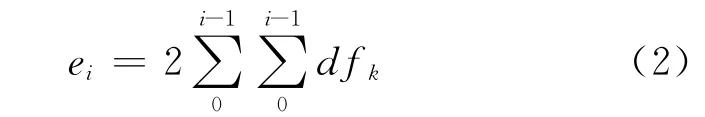
2.2.2 绳正法拨后正矢偏差分析

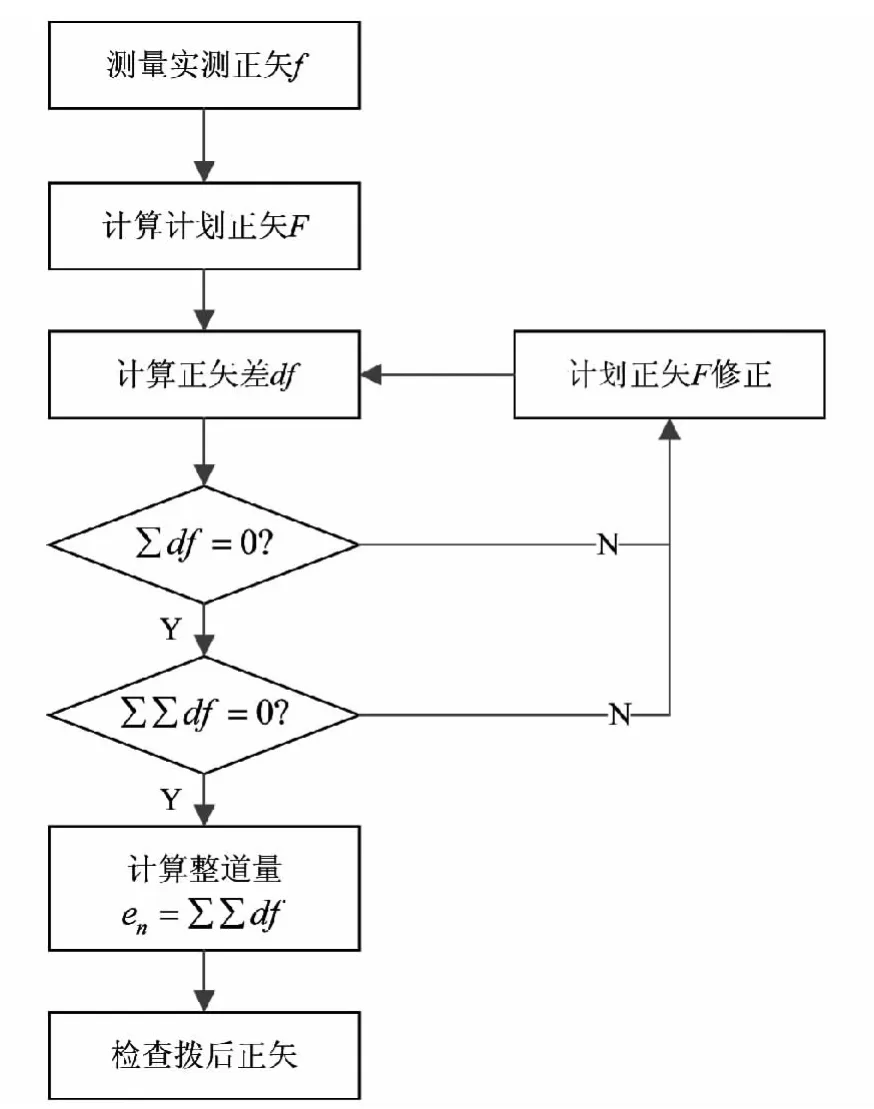
图1 曲线整道计算流程［4］Fig.1 Calculation flow chart of curve realignment

2 绳正法整道的性态与误差分析

2.1 绳正法整道的性态

测量精度与拨量间误差传递关系量与其线性方程组的性态有关，而条件数是刻画方程组性态的重要指标。若条件数小，则说明方程组计算对原始数据扰动不敏感，方程组为“良态”；若条件数随矩阵规模的增大而急剧增大，则说明方程组计算对数据扰动敏感，方程组为“病态”。作为线性方程组的解对数据误差敏感性的度量，本文将对式（2）的条件数进行分析。

文献［11］给出了相应的算例，当n＝20，σ＝0.1mm时，调整量标准不确定度σ（en）＝10.7mm。即意味着在曲线尾难以满足∑fi与∑Fi闭合的要求，需对计划正矢修正。

其中：E为拨量，mm；G为系统矩阵；F为正矢差，mm。

（一）多角度解读现象包含的各种道理——从知识角度上分析同一信息往往包含许多方面的道理，政治课主要是分析信息背后反映出来的政治、经济、文化、哲学几个方面的道理。

（3）井底板及接缝漏水，可采用水泥或化学注浆补漏处理。如大而积渗漏水，可将渗漏部位凿毛，洗净、湿润，抹压1-2 mm厚素水泥浆层，再用防水砂浆或膨胀水泥砂浆抹而，或用刚性防水多层抹而补漏。在内部净宅允许的情况下，亦可在内部加设60-80 mm厚细石防水混凝土套紧贴底板及刃脚部位，以阻止防渗漏水。

对于线性方程组，条件数cond（G）定义为

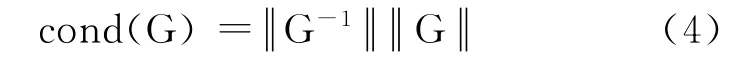
因为上（下）三角Toeplitz矩阵的逆矩阵仍然为上（下）三角 Toeplitz矩阵，可知，G－1依然为一下三角的Toeplitz矩阵。定义G－1如下：

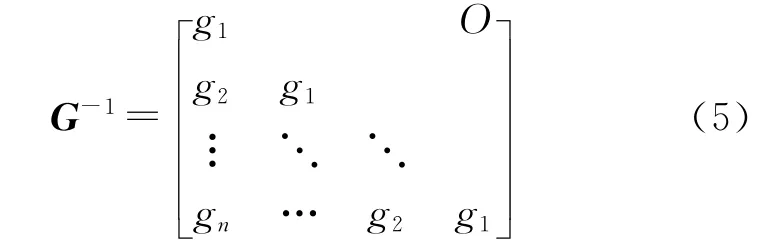
其中［12］

随着创新2.0时代和工业4.0时代的到来，高校要因势利导，通过多元化的教学方式来对大学生进行符合时代要求与学生发展的企业家精神教育实践活动。

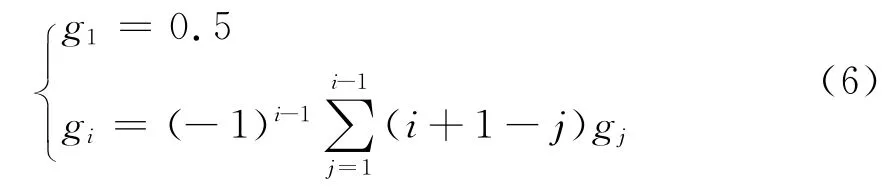
由于范数的等价性并为便于计算，取矩阵的1范数，可得，

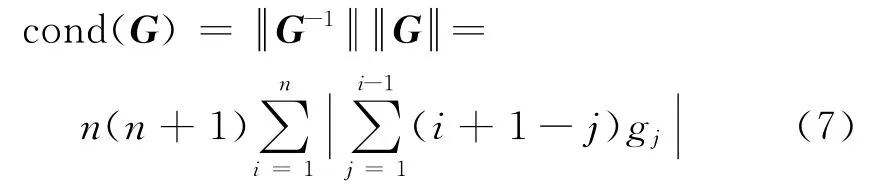
2.2 绳正法拨量的误差分析

当n＞3时，

2.2.1 曲线拨量不确定度分析

由式（2），设实测正矢fi的测量独立且等精度，其标准不确定度σ（fi）为σ，依据不确定度传播律测桩n处拨量en的不确定度σ（en）［11］：

可知，系统矩阵G为一下三角的Toeplitz矩阵。

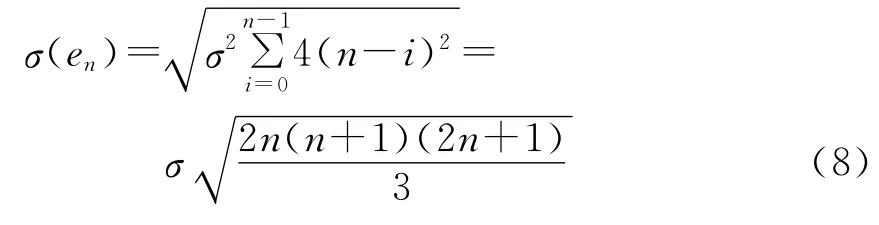
由式（7）可知，cond（G）的值与矩阵规模有关，即G呈病态；对于绳正法而言，其计算结果随测桩号的增加显著变化，为拨量计算带来不确定性。这种不确定性可用不确定度来衡量。关于拨道计算的效果，至少应包含以下2个方面，一是曲线尾拨量闭合条件的不确定度，二是曲线拨后正矢偏差不确定度。

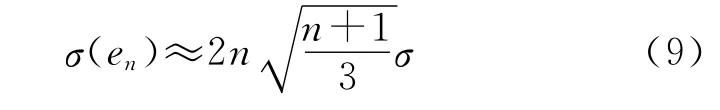
由文献［11］，式（2）可写作向量形式

为保证曲线整正前后两端的切线方向、曲线整正前后始终点位置、以及某些控制点（如小桥、道口等）位置不变，拨道计算中设置了一些限制条件，如要求等［7－8］。绳正法整道计算流程如图1所示。然而，或源于测量或源于计算，或是因为线路的既有状态，这些限制条件在实际整道作业中未必能全部满足。为保证限制条件，可对计划正矢进行修正并形成了一些经验方法［6，9－10］。计划正矢的修正意味着线路参数的改变，以R＝3 500m的平面曲线为例，当计划正矢修正1mm，则R在3 270～3 760m范围内变化；且正矢修正严重依赖于操作者的经验，客观上限制了绳正法在高速铁路上的应用。

实例 3：“I advised Mr.Darcy,and Lizzy,and Kitty,said Mrs.Bennet,to walk to Oakham Mount this morning.It is a nice long walk,and Mr.Darcy has never seen the view.”

不考虑实测正矢fi的精度问题，采用式（2）应能保证测桩n内每一点的平顺性。然而式（2）是采用累和的方法计算每个测桩i的拨量，即前i－1点的误差都将引入到当前点，这给拨道效果带来不确定性。由于曲线正矢计算采用的是中点弦测模型，此时测桩i的正矢修正量应为：

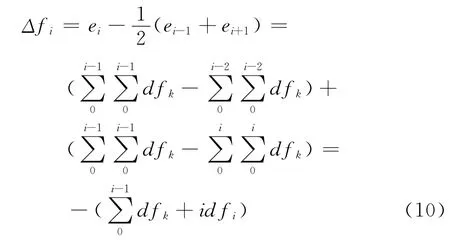
如前，设实测正矢fi标准不确定度σ（fi）为σ，拨后正矢偏差的标准不确定度

(3) 基础混凝土主要处于受压状态，最大压应力为16.9 MPa，根据混凝土相应规范[16]，C40混凝土设计轴心抗压强度19.1 MPa，满足极限荷载下基础承载性能要求；混凝土基础第一主应力最大值为0.34 MPa，发生在下锚板附近以下0.3 m范围内混凝土区域；高强灌浆层下部0.3 m范围内部分混凝土第一主应力接近于零。

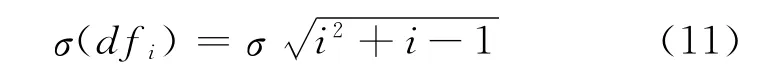
可知，拨后曲线的正矢偏差与0号测桩的距离有关，随着测桩号i的增加，拨后轨道正矢的不确定性增加。

3 绳正法在高铁曲线整正中的适用性

依据《高速铁路有砟轨道线路维修规则（试行）》［13］，整道后的正矢应满足作业验收标准，如表1所示。

为了验证实验装置测量的准确性，对正入射金属铝材料粗糙表面的测量数据进行了高斯拟合和几何光学近似逼近，得到了正入射情况下材料表面的散射光强,如图3和图4所示。

表1 线路曲线正矢作业验收容许偏差管理值Table 1 Ordinates tolerance of track planning works acceptance mm

以容许偏差不大于±2mm为例，讨论绳正法计算对曲线平顺性的影响。不计拨道作业的兑现率问题并认为通过修正计划正矢已满足闭合条件，如偏差不大于±2mm（95%概率），则可假定正矢容许的标准不确定度为1mm。并假设实测正矢的标准不确定度分别为0.05，0.1和0.3mm，按式计算满足作业验收标准的测桩数。

如图2所示，若实测正矢不确定度为0.3mm，则当到3号测桩时，计算的拨量有可能不能满足高铁的作业验收标准。而以均匀分布计，传统的钢尺、弦线测量正矢，其标准不确定度已达0.3mm。若采用绳正法来恢复曲线的圆顺，除采用更精密的测量工具外，还可以采用多次测量求均值或加密桩点等方法。即使如此，绳正法依然不适合高铁曲线的长撬整道。另外，作业后效果应现场回检并补调。

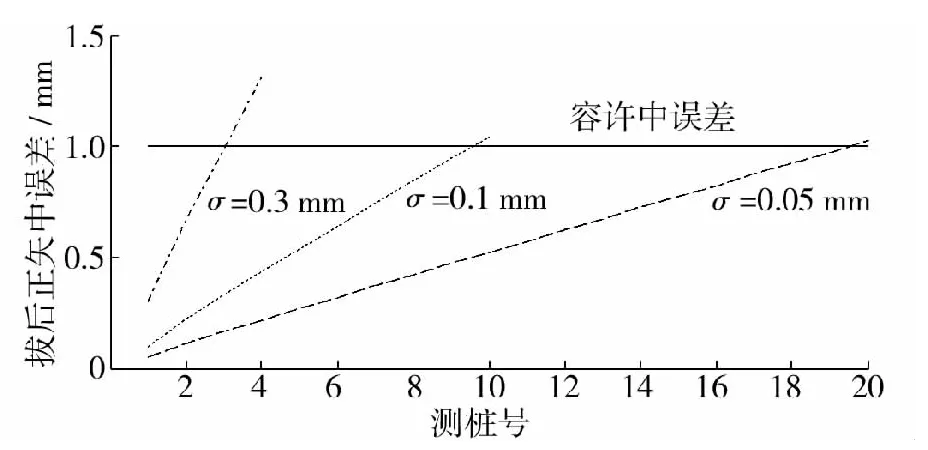
图2 绳正法下的实测正矢与拨后正矢偏差关系Fig.2 Schematic of existing ordinate errors and corrected ordinate errors by string lining method

4 结论

（1）通过建立绳正法的向量模型并分析其性态，可知绳正法的系统矩阵为病态，其结果受数据扰动的影响很大；

（2）对绳正法的误差传递关系的分析表明，源于渐伸线算法的累和计算，绳正法的拨量误差以及平顺性误差均随测桩号的增加而增加；

黄土高原是世界上最大的黄土堆积区，占世界黄土的70%，但其植被覆盖稀疏，加之降水集中多暴雨，水土流失十分严重，黄土高原的综合治理是国家改造自然工程中的重点项目，以水土保持为中心的治理方针，将改土与治水相结合，治坡与治沟相结合，工程措施与生物措施相结合，实行农林牧综合发展，目前这种治理措施已经取得了明显成效。

（3）以高铁作业验收标准来分析绳正法的适用性，可知其仅适合于短撬作业，若要保证高铁曲线的圆顺，应采用其他算法。

［1］黎浩廉.对整正既有曲线的几个问题的探讨［J］.长沙铁道学院学报，1980，（1）：30－40.

LI Haolian.Some question analysis for curve realignment in the existing railroads［J］.Journal of Changsha Railway Institute，1980（1）：30－40.

［2］郝瀛.改建既有线平面时对曲线传统拨距法的误差分析［J］.铁道学报，1984，6（1）：71－83.

HAO Ying.Error analysis of the conventional shift computation method for curves in the reconstruction of existing railroads［J］.Journal of China Railway Society，1984，6（1）：71－83.

［3］刘永孝，刘学毅，张咏军，等.铁路既有曲线整正计算中基于坐标法的渐伸线误差分析研究［J］.铁道学报，2012，34（4）：82－87.

LIU Yongxiao，LIU Xueyi，ZHANG Yongjun，et al.Study on involute errors in computation of existing railway curve realignment［J］.Journal of the China Railway Society，2012，34（4）：82－87.

［4］童大埙.铁道轨道［M］.北京：中国铁道出版社，1988：243－251.

TONG Dayun.Railway track［M］.Beijing：China Railway Publishing House，1988：243－251.

［5］EASA S M.Practical optimization model for realigning railway horizontal curves［J］.Civil Engineering Systems，1991，8（1）：27－36.

［6］吴耀庭.铁路曲线及其养护［M］.北京：中国铁道出版社，2001：81－114.

WU Yaoting.Railway curve and its maintence［M］.Beijing：China Railway Publishing House，2001：81－114.

［7］Dwyer Wyer D O.Realignment of railway curves［J］.Proceedings of the ICE－Transport，1997，123（4）：234－240.

［8］李伟，蒲浩，彭先宝.基于方向加速法的铁路既有线平面重构优化算法［J］.铁道科学与工程学报，2009，6（3）：47－51.

LI Wei，PU Hao，PENG Xianbao.Existing railway plane line reconstruction algorithm based on direction acceleration method［J］.Journal of Railway Science and Engineering，2009，6（3）：47－51.

［9］Thadani Hadani M.Railway curves：their alignment and realignment［J］.Institution of Eng （India）Journal，Civ Eng Div，1972，52（9）：227－239.

［10］邓昌大.铁路曲线正矢合计闭俣差分析与处理探讨［J］.铁道建筑，2006（3）：76－77.

DENG Changda.Misclosure analysis and processing of railway cuve versine summation［J］.Railway Engineering，2006（3）：76－77.

［11］魏晖，吴仕凤，朱洪涛.基于相对测量调轨的高速铁路有砟线路整道技术研究［J］.铁道标准设计，2013（8）：11－15.

WEI Hui，WU Shifeng，ZHU Hongtao.Engineering trial of relative measuring adjustment method for HSR ballast rail maintenance［J］.Railway Standard Design，2013（8）：11－15.

［12］《数学手册》编写组.数学手册［M］.北京：人民教育出版社，1979：127－133.

Mathematics handbook compile group.Mathematics handbook［M］.Beijing：People’s Education Press，1979：127－133.

［13］铁道部运输局.TG／GW116－2013，高速铁路有砟轨道线路维修规则（试行）［S］.北京：中国铁道出版社，2013.

Transportation bureau of MOR.TG／GW116－2013，High speed railway maintain rules for ballast track（for trial implementation）［S］.Beijing：China Railway Publishing House，2013.