基于模糊理论的财务数据分析法

2014-01-01胡苏华

船舶与海洋工程 2014年3期

胡哲，胡苏华

（安徽工业大学，安徽马鞍山 243002）

0 引言

随着我国经济的高速发展，企业规模不断扩大。有效利用财务数据，及时掌握企业的经营状况和财务状况，对于企业管理有着至关重要的作用。本文主要讨论如何使用模糊理论，并结合因数分解法进行财务数据分析，以说明基于模糊理论的财务分析理论的可行性和优越性。

1 因数分解法

在财务数据分析过程中，当不能直接得出有关数据的变动原因，或者需要对有些数据进行差异分析时，须引入因数分析法，以提高整体分析效率[1]。

因数分解法是对于某一财务比率变动原因进行分析的一种数学分解方法，通过此方法可以方便地分析出该比率变动的主要原因和次要原因，然后展开相关的分析过程。

因数分解法的理论基础就是泰勒公式的推广，或者说是建立在这一理论基础之上的[4]。先对这种方法予以简单说明：令y1=a1×b1和y2=a2×b2，然后求y1与y2的商值，如式（1）所示：

此外，当财务数据之间是相加的关系时，也可以进行函数的重新构造，将等式左右两边同时取指数，即构造新函数ey=ea+b=ea⋅eb，然后再使用因数分解法对于其展开处理，使用上述类似的方法，分析其变化原因，进而得出有关的结论。而对于同时含有乘法和除法的等式，直接对每一部分使用因数分解法进行分解，即对于乘法部分使用因数分解法分解，加法部分在上述同时取指数的基础上，再进行因数分解法分解，即可实现对财务数据的分析。所以该方法无论是对于乘法或者加法运算都是适用的，这是该方法的优越性，为后期计算机编程的简化，提高软件编程效率提供了理论基础。

2 模糊理论

模糊理论的主要思想是使用模糊集合描述事物，此概念很快为科技工作者所接受。

2.1 模糊集合

模糊集合的思想就是将人的判断、思维过程使用简单的数字形式直接表示出来，为人类提供了能充分利用语言信息的有效工具[2]。模糊集合是模糊理论思想的核心之一，对于财务数据来说，使用模糊集合的思想，就可以简化有关财务数据的分析过程，提高分析的效率、分析的准确率。

2.2 隶属函数

隶属函数可以很好地描述事物的模糊性，是对于模糊概念的定性描述，也是模糊理论的基础之一。对于同一个模糊概念，实际使用过程中不同的人将会使用不同的隶属函数，但是却可以反应同一模糊概念[3]。

3 基于模糊理论的财务数据分析原理

图1是基于模糊理论的财务数据分析原理。经过该理论方法的处理，可以实现对相关财务指标的评价，把财务分析人员从大量的财务数据中解放出来，提高工作效率。

3.1 数据的存储

运用相关会计理论和方法，应用财务指标的数据统计方法将有关的财务指标及相关数据计算出来，并将其存储与记录，以供财务分析时使用。此过程应当保证数据的真实、可靠、准确，消除会计处理方法对于财务指标的影响，以便客观地反映企业的相关财务状况和经营情况，保证整体财务分析的准确度，降低错报发生的可能性。

图1 基于模糊理论的财务数据分析原理

3.2 因数分解法处理

将得到的财务指标数据使用因数分解法进行处理，得到财务指标差异变量，消除其中异常的部分，然后进入下一步模糊化处理。

3.3 模糊化处理

利用模糊集合的概念，运用隶属函数将其模糊化处理，得到需要的模糊值。将通过下文的实例论述此处理过程。

在实际使用过程中，可以对不同的财务指标差异变量，使用不同的模糊子集变量加以描述，以使其更加符合实际情况，使得分析结果更加准确。

经过对财务指标差异变量的模糊化处理，可以实施对于财务指标的评价，供决策者使用。

3.4 决策者使用

通过上述技术处理，得到财务指标差异变量的模糊化取值，也就是实现了对该指标的评价。决策者可以结合实际情况，实现对企业某一部分运行情况的了解，及时发现问题，解决问题。

为了更有效地说明该方法，将以杜邦分析法为例，结合相关上市公司的财务数据，展开基于模糊理论的财务数据分析的实例解析，以说明该方法的合理性和优越性。

4 杜邦分析法

杜邦分析法（净资产收益率）是最有名的财务综合指标分解方法之一，它将产生企业效益的各个环节如生产、经营、管理、销售分解成相应指标，并且将它们再综合起来，揭示企业获取收益的内在因素及其相互之间的关系[4]。杜邦分析法主要是从企业的净资产收益率出发，将其分解成若干财务指标，从而形成了“杜邦指标分解体系”[5]。

净资产收益率是净收益除以所有者权益平均余额后的比率。该比率反映的是所有者权益的剩余报酬，是企业经营业绩的重要衡量指标[6,7]。基本分解过程如下：

即净资产收益率=销售利润率×总资产周转率×权益乘数

为了更好地说明该方法的优越性和合理性，选取马鞍山钢铁公司2011年的财务报表数据进行相关的论述与分析。

4.1 因数分解法处理

由于因数分解法必须使用两期的数据加以对比，为此将使用财务报表中的2011年和2010年的两期财务数据，然后对其使用因数分解法分解。将表1数据使用因数分解法分解，所得处理结果如表2所示。

通过这样的处理，可以得到差异数据，一方面消除了不同差异变量分析次序不同所带来的差异，另一方面也为下文的模糊理论的分析带来可能。

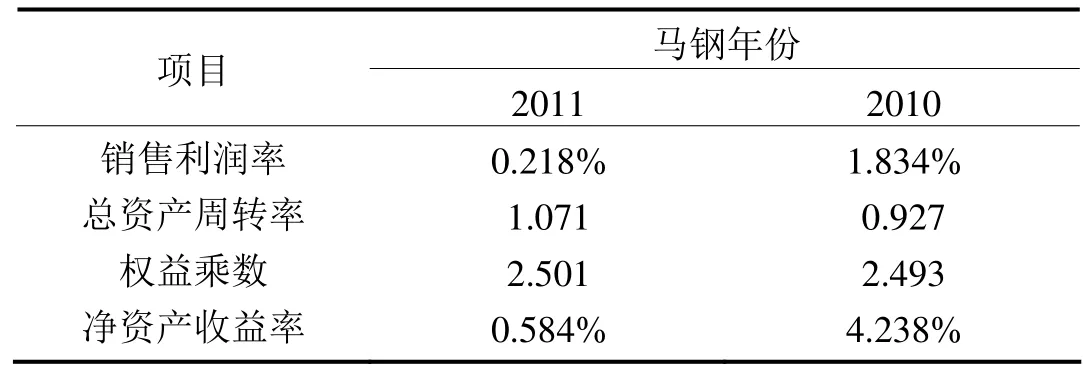
表1 杜邦分析法处理

表2 因数分解法分解

4.2 数据模糊化

依据模糊理论的思想，将经因数分解法分解之后的数据的论域都量化为13个等级，即都为{-3，-2，-1，-0.5，-0.2，-0.1，0，0.1，0.2，0.5，1，2，3}。其模糊子集都为{NB，NM，NS，ZE，PS，PM，PB}，它们分别代表{很差，比较差，差，一般，好，比较好，非常好}。

4.2.1 定义模糊隶属度函数

由于三角形隶属函数的灵敏度强、分辨率高，因此对于以上的差异变量，都采用三角形隶属函数。

三角形隶属函数主要由3个参数，分别为a，b，c确定，即：

为了突出某些变量的重要性，或者弱化某些变量的变化，也可以采用其他的隶属函数，例如高斯型隶属函数、S型隶属函数、梯形隶属函数等。

4.2.2 数据模糊化计算

表3 差异变量模糊集划分

使用三角形隶属函数，主要采用式（2），对于上述4个指标依次进行计算处理，计算其隶属度的取值。此过程中，将隶属度转化为模糊集中的某一变量。最后，使用表3差异变量模糊集划分表，对数据进行划分。即将计算出来的隶属度取值与该表进行比较，得到该差异变量的模糊集变量。此过程中，应结合不同企业的实际情况，借助经验常识，对表中的变量取值进行适当地调整。

各个财务指标差异变量的隶属度值如表4所示。同时，为了更好地提供给使用者使用，将隶属度取值模糊化，此过程应结合表3的数据，依次得到模糊取值为NB、PS、ZE、NB，即为很差、好、一般、很差。

表4 各财务差异变量的隶属度值

4.3 决策者使用

将经过以上处理的财务指标差异变量提供给有关决策者使用，通过模糊化的指标，不难看出净资产收益率相对于前一年度而言，是差的，说明整体企业的收益水平有所下降。其中，销售利润率方面必须加以关注，因为其指标模糊化后的模糊集取值为很差，因此必须加强对销售利润率的管理，采取有力措施提高销售利润率。对于总资产周转率来说，得到了一定程度的改善。此外，权益乘数指标几乎与前一年度趋平，说明企业的债务权益比率在过去的一年中并没有多大的改变。