波形钢腹板预弯工形梁的试验研究

陈卓异 黄 侨 杨 明

(东南大学交通学院,南京210096)

已有研究表明[1],通过剪力键连接的钢梁与混凝土顶板能够很好地组合在一起协同工作,并充分发挥这2种材料的优点.在组合T梁的下缘浇筑一期混凝土,采用预弯技术对下缘混凝土施加预压应力,能有效提高主梁的抗弯刚度,充分发挥钢材的抗拉强度.采用波形钢腹板代替平钢板,能有效防止钢腹板发生局部或整体失稳,不需要设置加劲肋.波形钢腹板的褶皱效应,使得徐变、收缩对应力重分布的影响也较小,可明显减少混凝土的预压应力损失.此外,采用波形钢腹板时,无需在腹板外包裹混凝土,可有效减轻结构自重.一种新型的组合结构——波形钢腹板预弯梁,兼顾了波形钢腹板和预弯梁的优点,具有结构变形刚度大、建筑高度低、桥头引道短、结构自重轻、外形协调美观的优点,在城市高架桥结构、轨道梁结构和高层建筑结构等建设领域具有一定的应用前景[1-2].

近年来,国内外学者对波形钢腹板组合梁的抗弯、抗扭和屈曲稳定等进行了较为系统的理论和试验研究[3-6],这些研究主要针对预应力混凝土箱形梁.Abbas等[7]对波形钢腹板I字钢梁施加平面内的荷载,公式推导了结构的扭转效应,并与计算机模拟值进行对比,但缺少试验验证和实测数据.另一方面,自从1987年首次引入预弯梁的概念后,各科研院所先后开展了预弯梁的研究工作.黄侨等[8]将研究成果应用于哈尔滨市5座立交桥,并提出了全时程时效分析方法,但是这些成果均基于传统的平钢腹板的预弯梁.本文将波形钢腹板与预弯梁结合起来,在试验室制作了波形钢腹板预弯工形梁的缩尺模型,并对其制作过程中每一阶段的应力和变形进行测试,采用静载试验对其主要的力学性能进行探索性研究.

1 试验

1.1 试验设计及材料性能

试验梁的梁长6.5 m,具体构造见图1.试验梁的底板混凝土即为一期混凝土,其强度等级为C50,配置有受拉钢筋5φ12 mm.顶板混凝土即为二期混凝土,其强度等级为C40,配置有受压钢筋4φ12 mm.箍筋直径为8 mm,间距为100 mm.预弯钢梁的顶底板和波形腹板均采用Q345钢板,顶底板外侧均设置有直径为13 mm、间距为150 mm的栓钉剪力连接件.

图1 波形钢腹板预弯工形梁的构造图(单位:mm)

试验室现场浇筑一、二期混凝土,并预留标准立方体试块与试验梁同环境养生.在第8天释放预弯力和第52天进行静载试验时,分别按照标准试验程序测试混凝土抗压强度平均值,结果见表1.通过材料拉伸试验,获取普通钢筋和钢板的屈服强度和极限抗拉强度平均值,结果见表2.

表1 实测混凝土抗压强度平均值 MPa

表2 实测钢材拉伸试验强度平均值

1.2 试验加载及测量方案

采用两点对称分级加载(见图2),加载点距离近端支座2.3 m,两加载点之间间距为1.8 m.采用50 t液压千斤顶施加荷载,并安装量程为50 t的荷载压力传感器进行精确读数.试验梁的支点、四分点和跨中位置处布置有竖向位移计.分别采用东华3815静态应变读数仪、TDS303静态应变读数仪和SW-LW-101型电子裂缝观测仪读取位移、应变和裂缝.

图2 试验加载及测试方案示意图(单位:mm)

2 试验梁的制作

利用有限元分析软件ABAQUS(V6.6)模拟试验梁的制作阶段和加载过程.整个模型中,波形钢腹板预弯钢梁被划分为5 367个减缩积分壳单元(S4R).一期和二期混凝土分别被划分为5 367和4 025个三维八节点减缩积分实体单元(C3D8R),钢筋被划分为1 920个杆单元(T3D2),钢筋嵌入在混凝土之中,钢板与混凝土之间采用Tie的方式耦合模拟剪力连接件[9].同时,借鉴现有的预弯梁计算理论[1],建立理论计算公式,分析试验梁的变形和应力分布.

2.1 钢梁预压阶段

为防止预压时钢梁侧倾失稳,同时放置2片钢梁,用缀板连成整体以增加其横向抗弯刚度.钢梁上搭设分配梁,在距梁端2.3 m的位置处施加预弯力,具体加载方式见图3(a).在试验室内先后对3组增加横向联系的双片钢梁进行预压,其钢梁尺寸和预压工艺完全相同,一共采集到3次预压数据.

同时,从ABAQUS有限元软件建立的整体模型中提取钢梁预压的模型,模拟钢梁的预压施工(见图3(b)).将3组钢梁预压的试验数据和在同样预压荷载作用下的有限元模拟值进行汇总，结果见表3.理论计算得到的跨中位移为35.7 mm,上下缘钢板的控制应力为258.7 MPa,与有限元计算(FEA)的位移和应力值吻合良好.有限元计算得到的跨中位移值与实测值相比,最大差值为6.2%,如要进行精确的线形控制,此误差不容忽视.有限元计算钢梁的上缘和下缘应力值与实测值的最大差值分别为4.7%和1.5%,整体较为一致.总体上来说,理论计算方法和有限元模拟均能较好地计算钢梁的预压过程.

图3 钢梁预压阶段

表3 预压荷载作用下钢梁的位移和应力

2.2 钢梁反弹阶段

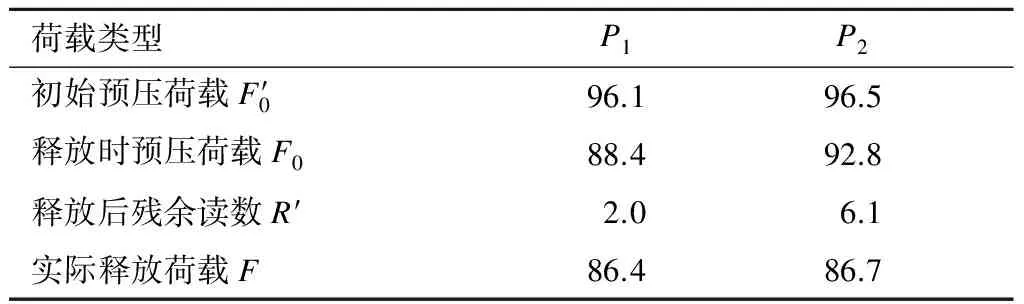
表4 实测PICS预压荷载的变化情况 kN

一期混凝土下缘在跨中和四分点处的应力情况如图4所示.跨中混凝土下缘的压应力达到12.9 MPa,为防止荷载作用下混凝土开裂提供了较为充足的压应力储备.另一方面,试验测得底板混凝土在下缘的压应力比理论计算值大3.2%,而四分点处混凝土下缘的压应力为8.1 MPa,比理论计算值小6.7%,理论与实测值的差距不大.同时可以发现,理论计算值与有限元模拟结果也较为一致.因此,整体上三者互相得到较好的验证,说明波形钢腹板预弯梁能有效地将预应力施加于混凝土上,而且普通预弯梁的理论计算方法仍然能适用于波形钢腹板预弯工形梁.

图4 一期混凝土下缘应力

3 试验梁静载试验分析

3.1 试验结果

在2个对称集中荷载作用下,试验梁跨中的荷载-挠度曲线可明显分为3个阶段(见图5).

图5 试验梁跨中的荷载-挠度曲线

1) 第1阶段(A-B)，即线弹性阶段.当试验荷载P小于开裂荷载Pcr时,预弯弯矩产生的预压应力值σ0与混凝土的抗拉强度之和大于荷载P产生的拉应力σ,即σ0+fc>σ.此时,钢筋和混凝土变形协调,试验梁的抗弯刚度为定值.跨中的挠度值与荷载呈线性关系.

2) 第2阶段(B-C)，即弹塑性阶段.当P=0.455Pu时,下缘混凝土开始出现裂缝,此时P即为开裂荷载Pcr,在60 kN时混凝土裂缝最大宽度为0.03 mm.随着荷载的增加,跨中裂缝垂直向上延伸,贯穿受拉钢筋.此时混凝土承受的拉力转移到钢筋中,钢筋的拉应力增长、突变.底板混凝土裂缝数量增加,间距趋于均匀,截面的抗弯刚度逐渐减小,中性轴的位置逐渐上移,跨中下挠速率随着P的增大而加快.当P=0.750Pu时,裂缝贯通底板混凝土,下缘裂缝宽度增加到0.16 mm,此时P即为贯通荷载Pct.荷载继续增加,裂缝无法延伸,跨中裂缝的数量基本不再增加,抗弯刚度基本恒定,挠度与荷载约为线性关系.

3)第 3阶段(C-D)，即塑性阶段.当P>0.917Pu时,进入塑性破坏阶段.此时底板下缘混凝土的裂缝宽度已经达到0.40 mm,继续加载,荷载增值很少,而且无法维持,顶板受压混凝土开始出现纵向裂缝.持续加载,直到挠度值为54.90 mm时,顶板混凝土部分崩碎(见图6(a)),荷载读数仪数值变小,但持续的加载仍能保持较大的承载力.试验梁在整个破坏过程中表现出较好的延性(见图6(b)),钢梁与上下混凝土翼板之间无可视的滑移,黏结性能良好.

分析试验梁跨中的荷载-挠度曲线,采用有限元通用软件ABAQUS模拟整个试验加载过程,钢材和钢筋的材料本构关系选用双折线理想弹塑性模型,并用非线性损伤塑性本构模型定义混凝土的材料性能,采用位移加载.计算与实测结果对比表明,有限元模拟的荷载-挠度曲线与试验测得的曲线吻合较好.

图6 试验梁的破坏形态

3.2 挠度分析

相比弯曲挠度,剪切挠度是微小量,但对于高跨比较大的梁(例如深梁)来说则是需要考虑的.文献[10-11]认为，波形钢腹板的剪切刚度相对较小,由剪切引起的竖向变形相对较大.文献[12]认为剪力流在腹板中为恒量.因此,提出如下的剪切变形挠度微分方程：

(1)

式中,x为挠度计算截面到近端支座的距离;tw,hw分别为波形钢腹板的厚度和高度;k为形状有关的系数,对于矩形k=1;G为钢板的剪切模量.当0

(2)

式中,l1为试验荷载到近支座的距离；Gw为等效剪切模量,波形钢腹板的换算公式为Gw=G/1.1.

因此,考虑弯矩和剪切共同作用的跨中挠度计算公式为

(3)

式中,M(x)为弯矩;E为弹性模量;I为抗弯惯性矩.

试验测试的开裂荷载约为56 kN,取开裂前的荷载历程,按照全截面抗弯刚度和弹性变形假定,采用ABAUQS软件和式(3)分别计算其跨中竖向挠度.由图7可知,采用式(3)计算的挠度曲线与有限元模拟的挠度曲线高度重合,数值差距不到1%.试验测得的跨中竖向挠度偏大,这是因为荷载-挠度曲线在混凝土开裂前也表现出少量的非线性.另一方面,对比剪切变形挠度与总挠度,试验梁的剪切变形挠度在混凝土开裂前占总挠度的22.4%,因此,进行正常使用极限状态的挠度验算时,宜考虑剪切变形的影响.

图7 开裂前一期混凝土跨中的荷载-挠度曲线

3.3 裂缝分布与开裂荷载

静载试验过程中,观察了4条主要裂缝的宽度发展情况(见图8).在对称荷载作用下跨中区域首先出现裂缝1和裂缝2.当荷载达到80 kN时,在加载区域附近出现裂缝3和裂缝4.当加载到120 kN左右时,裂缝增幅突然变大,试验梁已经无法继续承载.试验结果表明,开裂荷载约为极限破坏荷载的47%,说明试验梁具有较好的抗裂性能.

图8 荷载-裂缝宽度曲线

通过平截面假设，建立内力与应力的关系方程,考虑制作过程中各阶段荷载的应力叠加和收缩、徐变的内力重分布,建立应力增量计算公式.由此可得开裂弯矩的计算公式为

Mcr=(γmneft+σel+σpl)Wcl

(4)

式中,γm为组合梁截面抵抗矩影响系数[9];ne为钢材弹性模量和混凝土弹性模量之比;ft为混凝土抗拉强度;σel为各阶段荷载的应力叠加值;σpl为收缩、徐变等塑性变形产生的应力损失[1];Wcl为预弯梁的截面对下缘的弹性抵抗矩.

根据开裂弯矩计算公式,在考虑塑性和不考虑塑性的情况下,其开裂荷载计算结果分别为75.5和62.1 kN,实测开裂荷载为56.0 kN.由此表明,若不考虑塑性,开裂荷载的计算误差达到34.8%;而考虑塑性应变产生的应力损失,其计算误差减小到10.8%,对于混凝土结构,该误差在可接受的计算误差范围内.塑性应变产生的应力损失为24.0%,必须考虑收缩、徐变等塑性应变的影响.

3.4 截面应变与极限承载力

图9为试验梁在跨中截面沿梁高方向的正应变曲线.仅顶板上缘和底板下缘的测点为混凝土的应变测点,其他测点皆为钢筋或钢板的应变测点.由图可知,顶板的应变曲线均为直线,满足平面变形协调,而底板在120和127 kN时应变曲线变成折线,这源于混凝土裂缝对应变测试的影响.不考虑腹板上的应变值,整体上可以认为截面变形符合拟平截面假设.

图9 跨中截面应变分布曲线

根据极限抗弯承载状态下的应变分布情况(见表5),引入以下假定来计算波形钢腹板预弯梁的极限承载力:① 不考虑一期混凝土开裂后的抗拉作用,不考虑波形钢腹板对抗弯刚度的贡献;② 构件变形采用平截面假设;③ 钢筋应力-应变关系采用完全弹塑性模型,在抗弯承载能力极限状态下,取用钢材的实测屈服强度和混凝土立方体强度平均值,并换算成棱柱体强度平均值.

表5 极限抗弯状态下的实测值与理论值

由水平力平衡条件可得

(5)

由于受压区高度x′小于混凝土板的厚度,故抗弯承载力的计算公式为

(6)

式中,h0为受拉区钢板和钢筋合力作用中心到混凝土受压区合力作用中心的距离.联立求解式(5)和(6),可得试验梁的抗弯极限承载力.

实测与理论计算的极限承载力分别为127.3和117.8 kN.由此可知,混凝土采用柱体抗压强度平均值,受拉区钢筋采用屈服强度平均值,受压区混凝土应力采用等效矩形应力计算模式,便可较准确地计算其极限抗弯承载力.

4 结论

1) 在预弯力作用下,波形钢腹板钢梁的腹板具有良好的稳定性,不需要设置加劲肋,施工较为方便.采用同时预压2片钢梁的方法,能有效防止钢梁整体侧倾失稳,并且简化制作工艺和加工设备.

2) 释放预压力后,试验梁跨中混凝土下缘的预应力可达到12.9 MPa,说明波形钢腹板钢梁能够有效地将预应力施加于底板混凝土之上.静载试验表明,波形钢腹板预弯工形梁的开裂荷载较大,具有较好的抗裂性.

3) 将实测值和计算结果进行对比,发现组合梁的剪切刚度主要由波形钢腹板提供,剪应力在腹板中分布均匀.混凝土开裂前试验梁的剪切变形挠度占总挠度的22.4%,因此,进行正常使用极限状态的挠度验算时,需要考虑剪切变形的影响.

4) 波形钢腹板预弯工形梁的预弯工艺为施工的主要难点.但是从综合效益而言,与预应力RC梁相比,其抗弯刚度大,建筑高度低,延性良好,力学机理明确,结构自重较轻,在城市桥梁中具有明显的优势.

)

[1] 黄侨. 桥梁钢-混凝土组合结构设计原理[M]. 北京: 人民交通出版社, 2004: 77-83.

[2] Staquet S, Rigot G, Detandt H, et al. Innovative composite precast prestressed precambered U-shaped concrete deck for belgium’s high speed railway trains[J].PCIJournal, 2004,49(6):94-113,134.

[3] 吴文清, 万水, 叶见曙, 等. 波形钢腹板组合箱梁剪力滞效应的空间有限元分析[J]. 土木工程学报, 2004, 37(9):31-36.

Wu Wenqing, Wan Shui, Ye Jianshu,et al. 3-D finite element analysis on shear lag effect in composite box girder with corrugated steel web[J].ChinaCivilEngineeringJournal, 2004,37(9):31-36. (in Chinese)

[4] 聂建国, 唐亮. 基于弹性扭转约束边界的波形钢板整体剪切屈曲分析[J]. 工程力学, 2008, 25(3):1-7.

Nie Jianguo, Tang Liang. Global shear buckling of corrugated steel plates with edges elastically restrained against rotation[J].EngineeringMechanics, 2008,25(3):1-7. (in Chinese)

[5] Driver R, Abbas H,Sause R. Shear behavior of corrugated web bridge girders[J].JournalofStructuralEngineering, 2006,132(2):195-203.

[6] 周绪红, 孔祥福, 侯健, 等. 波形钢腹板组合箱梁的抗剪受力性能[J]. 中国公路学报, 2007, 20(2):77-82.

Zhou Xuhong, Kong Xiangfu, Hou Jian, el al. Shear mechanical property of composite box girder with corrugated steel webs[J].ChinaJournalofHighwayandTransport, 2007,20(2):77-82.(in Chinese)

[7] Abbas H, Sause R, Driver R. Behavior of corrugated web I-girders under in-plane loads[J].JournalofEngineeringMechanics, 2006,132(8):806-814.

[8] 黄侨, 吴红林, 陈雪枫. 预弯组合梁桥的全时程时效分析理论及其应用[J]. 哈尔滨工业大学学报, 2003, 35(5):615-620.

Huang Qiao, Wu Honglin, Chen Xuefeng. Preflexed beam bridges long-term properties analysis theory and its application [J].JournalofHarbinInstituteofTechnology, 2003,35(5):615-620.(in Chinese)

[9] Lebeau K, Wadia-Fascetti S. Predictive and diagnostic load rating model of a prestressed concrete bridge [J].JournalofBridgeEngineering, 2010,15(4):399-407.

[10] Ikarashi K, Kozaka K, Nakamura Y. Plastic deformation capacity of corrugated web girder under shear bending[J].JournalofStructuralandConstructionEngineering, 2012,77(673):443-451.

[11] 贺君, 刘玉擎, 陈艾荣, 等. 折腹式组合梁桥考虑剪切变形的挠度计算[J]. 同济大学学报:自然科学版, 2009, 37(4): 440-444.

He Jun, Liu Yuqing, Chen Airong, el al. Deflection calculation of composite girder bridge with corrugated web with consideration of shear deformation[J].JournalofTongjiUniversity:NaturalScience, 2009,37(4): 440-444. (in Chinese)

[12] Chen Zhuoyi, Huang Qiao, Yang Ming, et al. Shear stress distribution and deflection of preflex I-girder with corrugated steel web [C]//Proceedingsofthe3rdInternationalConferenceonCivilEngineering,ArchitectureandBuildingMaterials. Jinan, China, 2013:1374-1379.